2. 瑞士南方应用科技大学 DTI部,瑞士 卢加诺 CH-6000
2. Department of Technology Innovation, University of Applied Science in Southern Switzerland, Lugano CH-6000, Switzerland
桥梁是决定交通通行能力和通行效率的关键枢纽, 是国家重要的基础设施和关系到社会、经济协调发展的生命线工程,近年来经济发展对桥梁结构的架设速度, 长期可靠性, 抗超载和抗疲劳等性能提出了更高的要求[1].纤维增强聚合物基复合材料(Fiber Reinforced Polymer,FRP)以其优良的力学性能和物理化学性能,在桥梁工程中的应用量在不断扩大[2].从上世纪70年代开始,FRP就开始在桥梁工程中尝试应用[3].英国,美国和以色列最先应用这种新型材料作为建筑和桥梁结构中的主要构件.70年代后期,我国也开始对FRP桥梁进行研究,当时大多采用的是GFRP[4].随着FRP在结构工程中被逐渐接受,FRP在桥梁结构中的应用迅速发展.
纤维复合材料的密度仅为钢的1/4~1/5,比强度为普通钢的20~50倍[5],是高强度合金的2~4倍.其工程性能具有下列优点:(1)对特种载荷可以进行优化设计;(2)减少结构的静载荷,增加结构的额定载荷;(3)减少维护成本,增加工作寿命;(4)现场不需要重型安装设备,减少安装成本;(5)施工速度快,减少交通中断时间;(6)增加结构的耐久性和抗断裂性能[5].FRP的主要缺点体现在其高聚物基体在火灾环境下容易被点燃,同时由于树脂基体的玻璃化温度较低(一般小于200 ℃),高温会导致树脂基体软化,FRP的力学性能下降,从而影响FRP桥梁的安全稳定性能.此外与传统结构材料不同,FRP制品通常为各向异性, 沿纤维方向的强度和弹性模量较高, 而垂直纤维方向的强度和弹性模量很低.由于FRP的各向异性, 在受力性能上还有许多不同于传统结构材料的现象, 如拉伸翘曲现象, 这些都会增加FRP结构的分析与设计难度[6-7].合理地将FRP应用于各类结构中已成为工程结构应用发展的重要方向.
TSCB (Twin Shape Composed Beam)是一座由一组空间对称模块组成的CFRP (Carbon Fiber Reinforced Polymer)三明治结构复合材料人行桥.TSCB项目是瑞士南方应用科技大学、广东工业大学、瑞士BLUE轻结构设计工作室、MIKI复合材料公司、AIRLIGHT公司以及瑞士提切诺州政府合作项目.瑞士提切诺州将是第一座TSCB人行桥的使用客户.本文是TSCB项目中前期有限元仿真工作的一部分,主要通过大型有限元软件ANSYS对TSCB人行桥梁进行强度分析以及在极限行人载荷下的跨中竖向挠度分析,并使用Tsai-Wu失效准则判定碳纤维复合材料的各层失效情况.
1 TSCB人行桥工程介绍FRP桥梁一般分为FRP结构桥梁和FRP组合结构桥梁两种[8].FRP结构是主要结构构件完全采用FRP材料组成的结构;FRP组合结构是指FRP材料与传统的结构材料,主要是混凝土和钢材,通过合理的组合共同工作来承受载荷的结构形式.TSCB人行桥是一座全FRP结构的人行桥.桥梁由6个完全相同的基本空间单元模块组成,每个空间单元模块又由上下对称的两个部分组成.TSCB人行桥全长18 m, 宽4.21 m,高2.408 m,整桥质量为602 kg.TSCB人行桥最突出的特点是创新的空间对称式模块化结构设计,使得TSCB人行桥相对传统的FRP桥梁具备更快的施工架设速度,桥梁可以完全以模块的形式在工厂里完成制造,整桥自重轻,结构稳定,承载能力强.图 1是TSCB人行桥的外形尺寸,图 2是TSCB人行桥组装示意图.
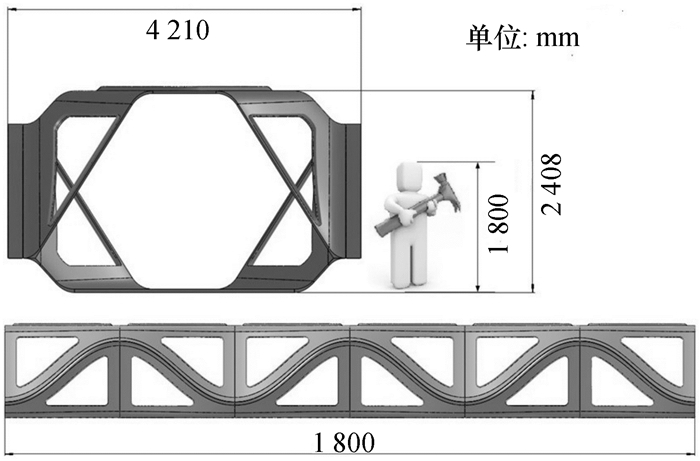
|
图 1 TSCB人行桥模型及尺寸 Figure 1 TSCB 3D-model and dimensions |
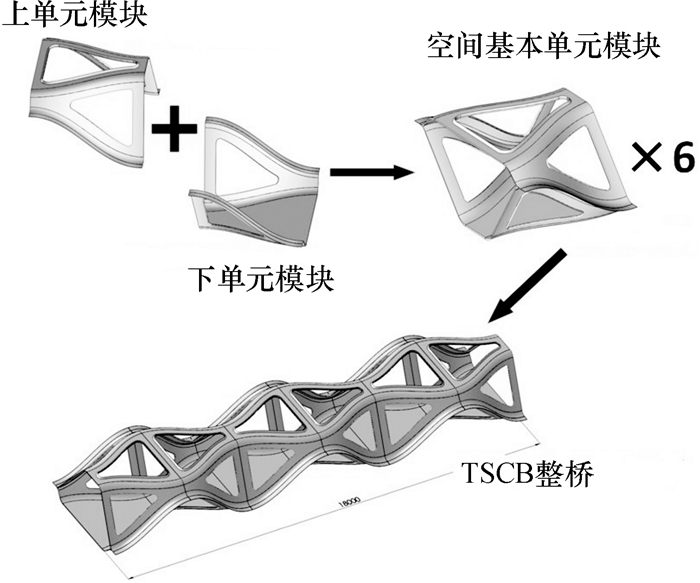
|
图 2 TSCB人行桥组装示意图 Figure 2 Assembly process of TSCB pedestrian bridge |
TSCB人行桥采用CFRP三明治夹层板结构.外层上下面为碳纤维层以及粘接层,中间是泡沫夹心层, 如图 3所示.上面层受压力,压缩变形,下面层受拉力,拉伸变形,而中间泡沫层主要承受剪切应力[9].该结构充分利用了面层CFRP材料强度,有很高的强度重量比和刚度重量比,是非常合理的构件形式[10].上下面的碳纤维层各为3层,上面铺层主方向角为0°、45°、90°,下面铺层主方向角为90°、-45°、0°.图 4为碳纤维各层铺层方向角示意图.外层碳纤维采用SAATI公司CC283-ET223碳纤维布, 胶接层采用3M公司9323B/A工业粘接剂, 夹心层为ARIEX公司C70.48通用结构泡沫.表 1和表 2分别是CC283-ET233和C70.48的材料力学性能参数:
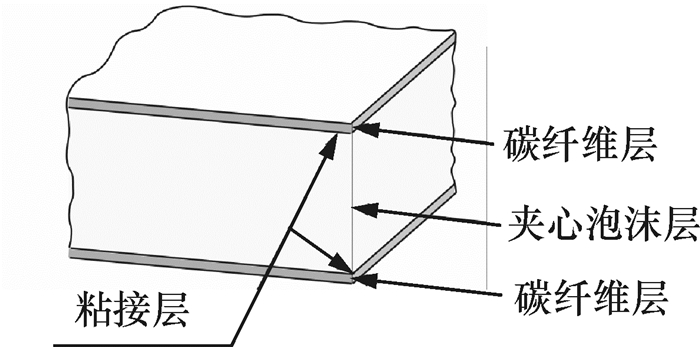
|
图 3 三明治夹层板结构 Figure 3 Sandwich structural boards |
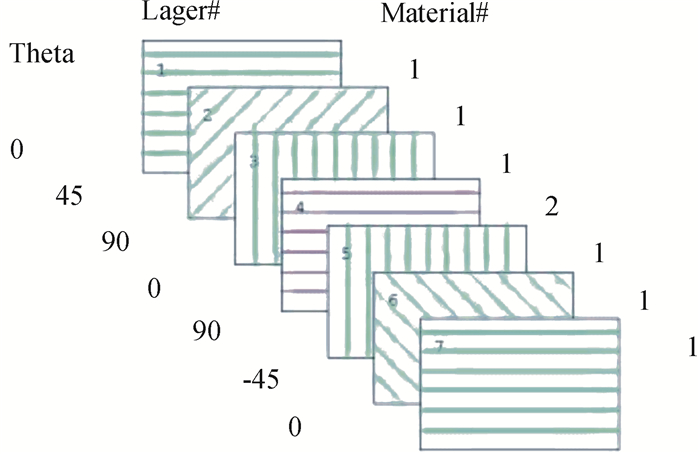
|
图 4 桥面板碳纤维铺层示意图 Figure 4 Carbon fiber layered configuration of bridge boards |
| 表 1 CC283-ET223碳纤维力学性能参数1) Table 1 Mechanical properties of CC283-ET223 |
| 表 2 C70.48通用结构泡沫力学性能参数 Table 2 Mechanical properties of C70.48 |
有限元分析方法作为一种成熟的技术广泛应用在土木工程中桥梁的静应力强度,共振稳定性以及疲劳失效等方面的仿真计算. ANSYS是一款大型可靠的有限元分析软件,提供了丰富的单元类型以及广泛的材料本构模型,可以模拟各种材料包括复合材料的力学特性.近些年来随着ANSYS功能的进一步完善,越来越多的设计研究人员在FRP复合材料桥梁设计过程中,使用ANSYS对桥梁进行有限元仿真分析,提高了效率和设计可靠性,是CAE领域的重要应用.
本文使用ANSYS APDL和Solidworks对TSCB人行桥梁进行有限元模型的建立,主要步骤包括:(1)在Solidworks软件中建立TSCB人行桥三维几何模型;(2)将TSCB人行桥三维模型导入ANSYS APDL中;(3)在ANSYS APDL中对模型进行前处理,包括模型修改、参数定义、材料设置和网格划分等.
在有限元单元类型的选择上,根据TSCB人行桥为多层复合材料以及薄壁的特点,主要采用非线性层合结构壳单元SHELL91和线性层合结构壳单元SHELL99单元[11].SHELL91支持塑性、大应变行为以及具有一个特殊的“三明治”选项[12],因此使用SHELL91单元模拟具有夹心结构的桥梁部分.在定义材料性能参数时,主要采用定义实常数的方式来模拟材料的性能,铺层角和铺层厚度.之后选择合适的单元尺寸进行网格划分,最终形成TSCB人行桥的有限元模型.需要特别注意的是TSCB人行桥外层是有铺层主方向角的碳纤维层, 在划分网格时必须控制好各单元坐标系主方向保持一致.TSCB人行桥桥底面板、桥顶和桥侧壁的泡沫夹心层厚度是不一样的,在设置铺层厚度时要注意区别设置.
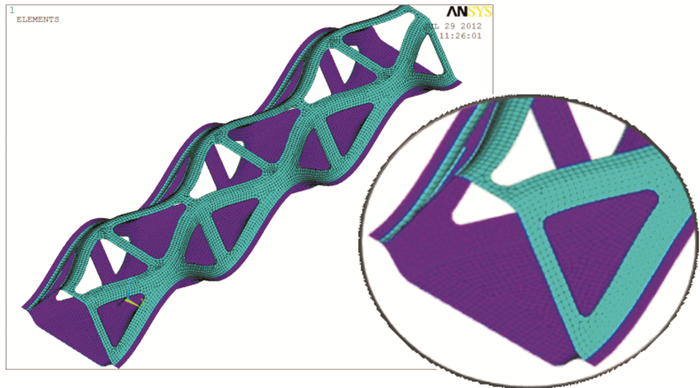
通过不同网格密度划分,对仿真结果数据进行对比,可知在网格尺寸达到0.05 m时仿真结果已经收敛.综合考虑仿真计算结果准确性和计算成本,本文中采用网格尺寸为0.05 m的有限元模型仿真结果数据作为参考.以下数据均是在此网格密度下的结果,有限元模型总单元数量为666 67个,总节点数为269 593个.图 5为TSCB人行桥有限元模型以及局部放大视图.
|
图 5 TSCB人行桥有限元模型 Figure 5 FEA model of TSCB pedestrian bridge |
FRP是正交各向异性材料.随着复合材料的广泛应用,众多学者将各向同性材料的强度准则以新的表现形式应用于复合材料,这些强度准则有最大应力(应变)准则、Tsai-Hill准则、Hoffman准则、Tsai-Wu失效准则和比应变能密度准则.Tsai-Wu失效准则是现有成熟准则中对复合材料的破坏描述最全面的准则,其他准则都可以根据特定的加载和受力条件将这一准则予以简化而得到[13].Tsai-Wu失效准则的理论依据是Tsai-Wu张量理论.
最大应力(应变)准则、Tsai-Hill准则、和Hoffman准则等强度理论与实验结果之间有不同程度的不一致,改善两者之间一致性的方法是增加理论方程中的项数.为此蔡和吴以张量形式提出新的强度理论(Tsai-Wu张量理论).他们假定在应力空间中的破坏表面存在形式为
| $ {F_i}{\sigma _i} + {F_{ij}}{\sigma _i}{\sigma _j} = 1, $ | (1) |
式中,Fi和Fij分别是二阶和四阶强度系数张量,除了σ4=τ23,σ5=τ31,σ6=τ12外,应用简写符号,此方程很复杂,Fi有6个系数,Fij有21个系数.对于平面应力下的正交各项异性单层材料,式(1)可化为
| $ \begin{array}{l} \;\;\;\;\;\;\;{F_1}{\sigma _1}{\rm{ + }}{F_2}{\sigma _2} + {F_6}{\sigma _6} + {F_{11}}\sigma _1^2{\rm{ + }}{F_{22}}\sigma _2^2{\rm{ + }}{F_{66}}\sigma _6^2{\rm{ + }}\\ 2{F_{12}}{\sigma _1}{\sigma _2} + 2{F_{16}}{\sigma _1}{\sigma _6} + 2{F_{26}}{\sigma _2}{\sigma _6} = 1. \end{array} $ | (2) |
如同Hoffman理论一样,上式中应力的一次项对拉压强度不同的材料是有用的,应力的二次项对描述应力空间中的椭球面时,是常见的项,F12,F16和F26项是新出现的项,它们用于描述1和2方向正应力之间及σ1σ6,σ2σ6之间的相互作用.
张量Fi,Fij的某些系数可用Xt,Xc,Yt,Yc,S确定,如1方向拉伸时,σ1>0,σ2=σ6=0,则有
| $ {F_1}{X_t} + {F_{11}}X_t^2 = 1. $ | (3) |
而压缩时有
| $ - {F_1}{X_c} + {F_{11}}X_c^2 = 1, $ | (4) |
其中Xt,Xc均取正值.联立式(3)和(4)求解得
| $ {F_1} = \frac{1}{{{X_t}}} - \frac{1}{{{X_c}}}, {F_{11}} = \frac{1}{{{X_t}{X_c}}}. $ | (5) |
同理
| $ {F_2} = \frac{1}{{{Y_t}}} - \frac{1}{{{Y_c}}}, {F_{22}} = \frac{1}{{{Y_t}{Y_c}}}. $ | (6) |
由于材料主方向的S与剪切应力σ6的正负号无关,因此可得
| $ {F_1} = {F_{16}} = {F_{26}} = 0, {F_{66}} = \frac{1}{{{S^2}}}, $ | (7) |
余下有待确定的张量系数F12是σ1σ2项的系数,它反映双向正应力的相互作用.此时式(2)变为
| $ \begin{array}{l} \;\;\;\;\;\;\;{F_1}{\sigma _1}{\rm{ + }}{F_2}{\sigma _2}{\rm{ + }}{F_{11}}\sigma _1^2{\rm{ + }}{F_{22}}\sigma _2^2{\rm{ + }}{F_{66}}\sigma _6^2{\rm{ + }}\\ 2{F_{12}}{\sigma _1}{\sigma _2}{\rm{ = }}1. \end{array} $ | (8) |
可利用一个σ2=σ6=σm而所有其余应力分量为零的双向拉伸试验,由此得出
| $ \left( {{F_1} + {F_2}} \right){\sigma _m} + \left( {{F_{11}} + {F_{22}} + 2{F_{12}}} \right)\sigma _m^2 = 1. $ | (9) |
将式(5)、式(6)代入式(9)解出F12:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{F_{12}} = \frac{1}{{2\sigma _m^2}}\left[ {1 - \left( {\frac{1}{{{X_t}}} - \frac{1}{{{X_c}}} + \frac{1}{{{Y_t}}} - \frac{1}{{{Y_c}}}} \right)} \right.{\sigma _m} - \\ \left. {\left( {\frac{1}{{{X_t}{X_c}}} + \frac{1}{{{Y_t}{Y_c}}}} \right)\sigma _m^2} \right]. \end{array} $ | (10) |
F12取决于Xt,Xc,Yt,Yc和双向拉伸破坏应力σm.
下面讨论F12.当应力增大到一定程度,单层材料将发生破坏,所以在应力空间中方程(8)应是一闭合曲面,它与σ6=0的坐标面的交线
| $ {F_1}{\sigma _1}{\rm{ + }}{F_2}{\sigma _2}{\rm{ + }}{F_{11}}\sigma _1^2{\rm{ + }}{F_{22}}\sigma _2^2{\rm{ + }}2{F_{12}}{\sigma _1}{\sigma _2}{\rm{ = }}1. $ | (11) |
应是闭合曲线,根据二次曲线的几何性质,它应当是椭圆,其必要条件为
| $ {F_{11}}{F_{12}} - F_{12}^2>0, 即 - 1<\frac{{{F_{12}}}}{{\sqrt {{F_{11}}{F_{22}}} }}<1. $ | (12) |
在实际应用Tsai-Wu张量理论时,有时取F12=0,但通过对玻璃/环氧等复合材料的计算表明,F12的影响不应忽略.如取
在ANSYS APDL中按GUI操作:Main Menu>Preprocessor>Material Props>Failure Criteria>Add/Edit可实现Tsai-Wu失效准则的设置.一共有12个系数需要填写,包括X,Y,Z 3个方向的拉应力强度和压应力强度;XY,YZ,XZ 3个平面内的剪应力强度以及应力耦合系数.因为取
依据客户设计需求初步设定极限行人载荷为4 000 Pa.载荷加载区域面积为30.36 m2,则载荷总大小为121 440 N,相当于152个质量为80 kg的行人同时在桥上行走,行人密度为5.06人/m2.挠度通常是控制FRP人行桥的主要参数,挠度控制过严,将造成结构中应力水平过低,从而造成较大的浪费.依据瑞士结构设计标准SIA260/261标准,考虑FRP桥梁和其他普通桥梁的区别以及客户要求,在保证TSCB行人桥不出现材料失效破坏的前提下,取极限行人载荷作用下跨中竖向最大挠度不超过L/200,即18 m/200=90 mm.
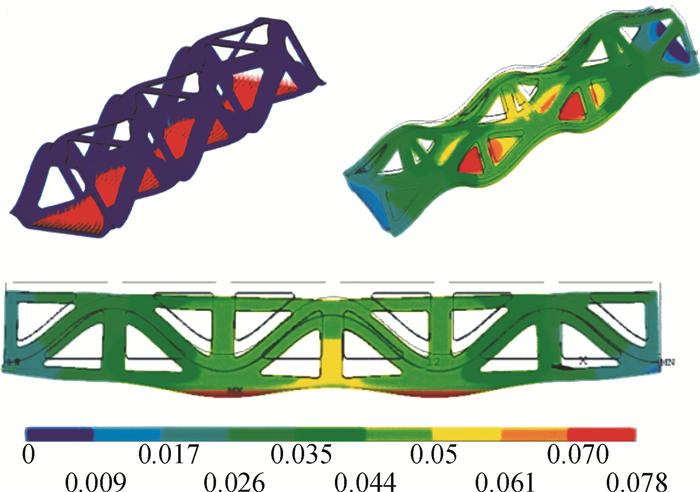
图 6中显示了TSCB人行桥极限行人载荷的加载区域(桥梁底部浅色区域)以及在极限行人载荷作用下TSCB人行桥的形变.可知在极限行人载荷作用下TSCB人行桥的跨中竖向挠度为78.465 mm.因为78.465 mm小于90 mm,所以TSCB人行桥满足低于最大跨中竖向挠度的要求.
|
图 6 TSCB人行桥在极限行人载荷下的变形 Figure 6 Deformation of TSCB under maximum pedestrian loads |
通过ANSYS APDL仿真计算后的彩色等值线反映的是
| 表 3 各层Tsai-Wu失效准则破坏因子范围 Table 3 Destroy factors range of Tsai-Wu failure criteria in each layers |
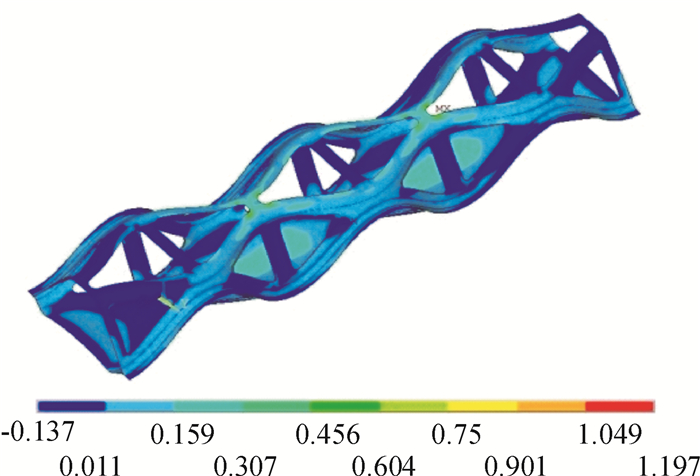
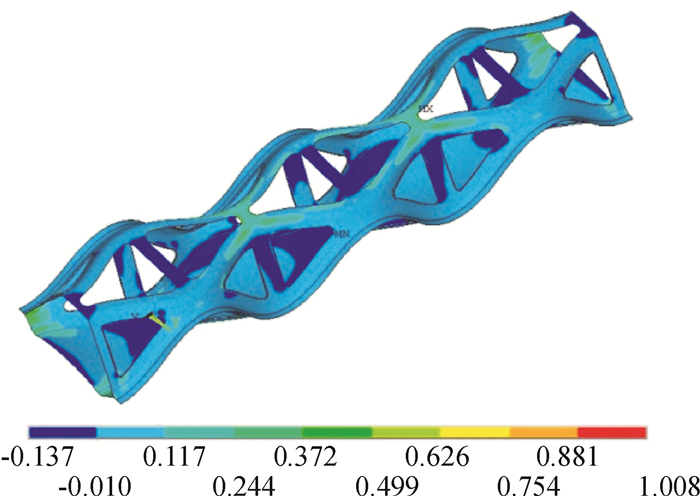
从表 3可以看出第1层、第2层、第3层和第6层的破坏因子最大值都大于1,碳纤维层材料发生了不同程度的失效破坏.从图 7至图 10中可以发现TSCB人行桥整体区域的碳纤维材料安全裕度较大,在极限行人载荷下不会发生失效破坏.对比各碳纤维层失效破坏区域可以发现,应力集中主要发生在TSCB人行桥梁顶部三角天窗孔的最小锐角区域,碳纤维复合材料的失效破坏都集中发生在该区域.因此可以在桥梁顶部三角形天窗边缘加强材料抗拉与抗压性能或者添加高强度的边框来防止应力集中造成的碳纤维材料的失效破坏.TSCB人行桥的第4层是夹心泡沫层,从表中数据来看泡沫层的强度满足要求,不会发生失效破坏.

|
图 7 TSCB人行桥第1层破坏因子云图 Figure 7 Destructive factor contour of TSCB in the first layer |
|
图 8 TSCB人行桥第2层破坏因子云图 Figure 8 Destructive factor contour of TSCB in the second layer |
|
图 9 TSCB人行桥第3层破坏因子云图 Figure 9 Destructive factor contour of TSCB in the third layer |

|
图 10 TSCB人行桥第6层破坏因子云 Figure 10 Destructive factor contour of TSCB in the sixth layer |
通过对TSCB人行桥在极限行人载荷下材料强度及挠度的有限元仿真分析得出以下结论:
(1) 在极限行人载荷的作用下,TSCB人行桥的跨中竖向最大挠度为78.465 mm, 符合低于L/200,即90 mm的设计要求.
(2) 在满足跨中竖向最大挠度要求的同时,以Tsai-Wu失效准则为桥梁复合材料失效判断依据,得出TSCB人行桥整体大部分材料强度满足要求,在极限行人载荷下不会发生材料的失效破坏.但是在桥梁顶部三角天窗最小锐角的局部区域应力集中,出现复合材料的破坏失效现象,因此建议加强该区域的复合材料强度,优化结构设计防止材料的失效破坏.
通过有限元仿真分析结果知道TSCB人行桥具备非常高的承载能力.桥梁全重602 kg,承重能力高达桥梁自重的20.3倍之多.
| [1] |
冯鹏, 金飞飞, 叶列平. FRP人行天桥的结构性能与设计指标研究[J].
建筑科学与工程学报, 2011, 28(3): 14-22.
Feng P, Jin F F, Ye L P. Research on structural performance and design indices of FRP footbridges[J]. Journal of Architecture and Civil Engineering, 2011, 28(3): 14-22. |
| [2] |
范海丰, 刘玉擎. FRP材料应用于桥面板的新技术[C]//第十八届玻璃钢/复合材料学术年会论文集. 北京: 中国硅酸盐学会, 2010: 123-129.
|
| [3] |
ACMA. Global FRP Use in Bridge Applicator[R]. New York: ACMA, 2004.
|
| [4] |
冯鹏, 李天虹, 李威, 等. FRP人行天桥结构设计与分析[J].
工业建筑, 2006(S1): 286-291.
Feng P, Li T H, Li W, et al. Structural design and analysis of an FRP pedestrian bridge[J]. Industrial Construction, 2006(S1): 286-291. |
| [5] |
杨勇, 可守峰, 徐博林, 等. FRP-混凝土组合桥面板疲劳性能研究综述[J].
西安建筑科技大学学报:自然科学版, 2010, 42(6): 781-789.
Yang Y, Ke S F, Xu B L, et al. Research status of the fatigue behavior of FRP-concrete composite decks[J]. Journal of Xi'an University of Architecture & Technology:Nature Science Edition, 2010, 42(6): 781-789. |
| [6] |
于锦生. 纤维复合材料在桥梁工程中的应用[J].
纤维复合材料, 2006(1): 49-52.
Yu J S. Application of Fiber composite materials in bridge project[J]. Fiber Composites, 2006(1): 49-52. |
| [7] |
咸贵军, 李惠. FRP复合材料土木工程应用与耐久性[J].
材料工程, 2010(z1): 121-125.
DOI: 10.3969/j.issn.1001-4381.2010.z1.025. |
| [8] |
冯鹏, 叶列平. FRP结构和FRP组合结构在结构工程中的应用与发展[C]//第二届全国土木工程用纤维增强复合材料(FRP)应用技术学术交流会论文集. 昆明: 中国土木工程学会混凝土与预应力混凝土分会纤维增强塑料(FRP)及工程应用专业委员会, 2002: 51-66.
|
| [9] |
张铟. FRP夹心桥面板桥梁静动态响应的数值分析[D]. 武汉: 华中科技大学, 2006.
http://cdmd.cnki.com.cn/article/cdmd-10487-2008024235.htm
|
| [10] |
Daniel Gay, Suong V Hoa, Stephen W Tsai. Composite materials design and applications[J].
CRC Press LLC, Paris, 2003.
|
| [11] |
Feldhusen J, Torsakul S. An approach to numerical modeling and simulation of cellular foam sandwich structures in commercial FE-softwares[C]. Proceedings of the 2008 IEEE IEEM Conference on Industrial Engineering and Engineering Management. IEEE, 2008: 836-841.
|
| [12] |
张朝晖.
ANSYS 12.0结构分析工程应用实例解析[M]. 3版. 北京: 机械工业出版社, 2010: 400-402.
|
| [13] |
左惟炜, 肖来元, 廖道训. Tsai-Wu准则用于三维编织复合材料矩形梁强度计算[J].
华中科技大学学报:自然科学版, 2006, 34(12): 74-76.
Zuo W W, Xiao L Y, Liao D X. Calculating the strength of 3D-braided composite rectangle beam by using Tsai-Wu criteria[J]. Journal of Huazhong University of Science and Techndogy:Nature Science Edition, 2006, 34(12): 74-76. |
| [14] |
沈观林, 胡更开.
复合材料力学[M]. 北京: 清华大学出版社, 2006: 62-63.
|
| [15] |
袁谱, 张攀, 冯鹏, 等. 变厚度FRP曲面夹芯板受力性能分析[J].
玻璃钢/复合材料, 2012(5): 9-18.
Yuan P, Zhang P, Feng P. A mechanical study for a FRP curve sandwich panel with varied thickness[J]. Fiber Reinforced Plastics/Composites, 2012(5): 9-18. |
 2014, Vol. 31
2014, Vol. 31

