随着我国城市化进程的加快和人居环境质量的提高,大量过街天桥及跨河人行桥得以不断建设,桥梁跨度亦不断增大,跨度的增加无疑导致桥梁结构越来越柔,使得在行人移动荷载作用下的振动往往超过限值要求,甚至产生共振现象.多重调频质量阻尼器(Multiple Tuned Mass Damper,MTMD)在建筑结构抗震与抗风领域的应用较为广泛,对于控制结构过大的振动响应具有很好的效果.Yun[1]采用MTMD有效控制了一42层超高层结构的风致振动响应;Hoang[2]针对一单自由度体系采用非线性数值求解器对MTMD系统的参数进行了优化分析;为保证在外界激励下TMD系统非线性运动方程能够得到精确数值解,Lee[3]和Chung[4-5]提出了TMD系统的参数优化设计理论和相应的TMD阻尼参数和频率参数的优化设计公式,并通过多个计算模型和台北101的实际工程分析对其进行了验证,取得了较好的效果;张旭升和王肇民[6]针对高耸钢结构电视塔采用MTMD进行了风振控制研究与设计,探讨了MTMD的基本动力特性及其主要参数变化对风振控制效果的影响;霍林生与李宏男[7]采用MTMD对人行过街天桥进行了振动控制分析,研究了MTMD系统对过街天桥竖向振动的作用;万信华[8]、余钱华等[9]对桥梁结构采用MTMD技术的地震动特性、车桥耦合振动特性等进行了研究,提出了相关理论计算公式,并对其基于实际工程进行了验证分析.文献[10-11]分别针对桥梁结构的可靠度优化和环境激励试验展开了相关研究.然而,MTMD技术对桥梁结构在人行荷载作用下的振动控制的研究文献还比较有限,且仍存在很多问题,如MTMD控制效果发挥的充分与否对频率比的依赖非常大,而实际工程在设计阶段很难准确预测桥梁结构的实际频率.为此,本文针对大跨悬索桥结构采用MTMD进行人行激励下的动力响应分析,探讨MTMD系统的动力特性及其参数变化对抑制结构动力响应的影响规律,并基于一实际桥梁结构验证MTMD系统对行人激励下的减振效果.
1 桥梁-MTMD体系运动方程假设桥梁上布置n个TMD装置,则桥梁-MTMD结构系统的运动方程可表示为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{M\ddot Y + C\dot Y + KY = P}}\left( {x, t} \right) + {\mathit{\boldsymbol{F}}_{{\rm{TMD}}}}\left( {x, t} \right), \\ {m_{di}}{{\ddot x}_{di}} + {c_{di}}\left[ {{{\dot x}_{di}} - \dot y\left( {{x_{0i}}} \right)} \right] + {k_{di}}\left[ {{x_{di}} - y\left( {{x_{0i}}} \right)} \right] = 0, \end{array} \right. $ | (1) |
式中, M、K、C分别为结构质量、刚度和阻尼矩阵;mdi、cdi、kdi分别为MTMD系统第i个TMD的质量、刚度和阻尼;Y为结构相对于地面的位移向量,即Y =[y1, y2, …, yn]T;xdi为MTMD中第i个TMD相对于地面的位移;P (t)和F TMD(t)分别为桥上人群动力荷载和TMD对结构施加的控制力.利用振型分解法,将桥梁的运动方程用广义坐标Xi(t)和振型函数φi(x)表示为
| $ Y\left( {x, t} \right) = \sum\limits_i {{X_i}\left( t \right)} {\varphi _i}\left( x \right), $ | (2) |
则当考虑第一振型时桥梁-MTMD体系的运动方程可简化为
| $ \left\{ \begin{array}{l} {{\ddot X}_1} + 2{\xi _1}{\omega _1}{{\dot X}_1}{\rm{ + }}\omega _1^2{X_1} = {P_1}\left( {x, t} \right) + {F_1}\left( {x, t} \right), \\ {{\ddot x}_{di}} + 2{\xi _{di}}{\omega _{di}}\left[ {{{\dot x}_{di}} - {{\dot X}_1}{\varphi _1}\left( {{x_{0i}}} \right)} \right] + \omega _{di}^2\left[ {{x_{di}} - } \right.\\ \left. {{X_1}{\varphi _1}\left( {{x_{0i}}} \right)} \right] = 0, \end{array} \right. $ | (3) |
式中, P1(x, t)=φ1(x)P(x, t)/M1,F1(x, t)=∑{2μdiζdiωdi[xdi-X1φ1(x0i)]+μdiωdi2[xdi-X1φ1(x0i)]}φ1(x0i),其中:M1为广义质量,ζ1、ω1分别为桥梁第一振型阻尼比和圆频率,ζdi、ωdi分别为第i个TMD的阻尼比和圆频率,μdi为第i个TMD的质量比(μdi=mdi/M1).
令P1(x, t)=e-jωt,联立式(3)的两个方程可得桥梁结构响应的传递函数:
| $ {H_{{X_1}\left( \omega \right)}} = \frac{1}{{ - {\omega ^2} + 2{\xi _1}{\omega _1}\left( {j\omega } \right) + \omega _1^2 - \sum\limits_{i = 1}^n {\frac{{{\mu _{di}}\varphi _1^2\left( {{x_{0i}}} \right){\omega ^2}\left[ {2{\xi _{di}}{\omega _{di}}\left( {{\rm{j}}\omega } \right) + \omega _{di}^2} \right]}}{{ - {\omega ^2} + 2{\xi _{di}}{\omega _{di}} + \omega _{di}^2}}} }}, $ | (4) |
则有结构位移放大系数为
| $ D = {H_{{X_1}\left( \omega \right)}}\omega _1^2 = \sqrt {\frac{1}{{{\rm{R}}{{\rm{e}}^2}\left( \lambda \right){\rm{ + l}}{{\rm{m}}^2}\left( \lambda \right)}}} , $ | (5) |
其中,
| $ \begin{array}{l} \;\;\;\;\;\;{\mathop{\rm Re}\nolimits} \left( \lambda \right) = 1 - {\lambda ^2} - \\ \sum\limits_{i = 1}^n {\frac{{{\mu _{di}}\varphi _1^2\left( {{x_{0i}}} \right){\lambda ^2}\left[ {\left( {\gamma _{di}^4 - \gamma _{di}^2{\lambda ^2}} \right) + 4\xi _{di}^2\gamma _{di}^2{\lambda ^2}} \right]}}{{{{\left( {\gamma _{di}^2 - {\lambda ^2}} \right)}^2} + 4\xi _{di}^2\gamma _{di}^2{\lambda ^2}}}, } \end{array} $ |
| $ {\rm{lm}}\left( \lambda \right){\rm{ = }}2{\xi _1}\lambda {\rm{ + }}\sum\limits_{i = 1}^n {\frac{{2{\mu _{di}}\varphi _1^2\left( {{x_{0i}}} \right){\xi _{di}}{\gamma _{di}}{\lambda ^5}}}{{{{\left( {\gamma _{di}^2 - {\lambda ^2}} \right)}^2} + 4\xi _{di}^2\gamma _{di}^2{\lambda ^2}}}} , $ |
| $ {\gamma _{di}} = \frac{{{\omega _{di}}}}{{{\omega _1}}}, \lambda = \frac{\omega }{{{\omega _1}}}. $ |
在人行桥设计规范中, 采用单人移动简谐共振荷载进行振动响应分析评估人致振动是最常用的方法.根据同济大学孙利民等[12]关于人行桥人行荷载振动激励的研究成果,单人竖向人行荷载Fv(t)的取值为
| $ {F_v}\left( t \right) = 0.36 \times 700\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right), $ | (6) |
式中:f0为桥梁结构的竖向自振频率(Hz),700为人的体重(N).
单人侧向人行荷载Fh(t)取值为
| $ {F_h}\left( t \right) = 0.009 \times 700\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right). $ | (7) |
桥上的行人经常是人群形式,人群中各人之间的相位、步频都不尽相同,精确的分析方式应该是基于概率分布的分析方法.考虑人行天桥上人群荷载存在以下几种工况:
1) 当桥上有一群人行走时,每个行人都具有相同的速度vs,步频fs.因此有vs=fsls,本文取行人的步行速度为1.5 m/s.假设桥上的行人能够自由地行走互不干扰,互不干扰的人群密度上限界定为0.5人/m2.根据Matsumoto等[13]对随机步行人群对人行桥激振的研究,假设行人上桥事件服从泊松分布,且步行相位互不相关,则人行桥上等效人数Np可采用式(8)计算.
| $ {N_p} = \sqrt n , $ | (8) |
式中, n为人行桥上按人群密度计算的行人总数.则人行桥总人群荷载为单人作用荷载乘以等效人数Np,竖向人群荷载为
| $ {F_{nv}}\left( t \right) = 0.36 \times 700{N_p}\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right). $ | (9) |
2) 当行人密度超过1.0人/m2时,因为行人前后间距变小,已不能自由地按本人意愿行走,高密度情况下,行人之间的步频已完全同步,只是相位不同,按照同样的随机概率分布模拟方法,采用式(10)所示高密度条件下等效人数计算公式计算.
| $ {N_p} = 1.85\sqrt n . $ | (10) |
3) 在人群极度拥密情况下,行人密度将超过1.5人/m2,会发生人群步频、相位“锁定”现象.锁定现象是在人群流动状态下,原先步频和相位均随机分布,同时也受到逐渐增大的振动的影响,进而导致越来越多的人进入步频、相位和楼盖振动完全同步的状态.此时,等效人数按式(11)计算[14].
| $ {N_p} = 0.2n. $ | (11) |
Matsumoto[13]通过研究指出室外人行天桥、走廊的振动加速度限值为5g%,超过该上述限值人体在结构上活动会产生不舒适的感觉,另根据英国BSI[15]规定,人体所能承受的竖向舒适度极限,用加速度表示为0.78 m/s2;因此,本文将一般人群移动荷载作用下产生的桥面振动加速度限值定为0.5 m/s2,将极端密集人群荷载作用引起的桥面振动加速度限值定为0.78m/s2.
3 桥梁-MTMD体系参数影响与减振效果分析 3.1 大跨悬索人行桥结构概况某人行桥工程采用主跨180 m的大跨悬索桥方案,跨径布置为36+180+36 m,主桥桥面总宽3.3 m,净宽2 m,立面图如图 1所示.该悬索人行桥采用纵横钢梁、主缆、吊杆、主塔和桥面板组合而成,横向钢梁采用工字钢Ⅰ4 000×250×20×20 mm,纵向钢梁采用工字钢Ⅰ300×150×15×15 mm,主缆直径40 mm,吊杆直径20 mm,主塔由4根1 200×1 200 mm钢筋混凝土柱组成.

|
图 1 大跨悬索桥立面图 Figure 1 Vertical view of the large-span suspension footbridge |
根据人行荷载模式及结构基本概况,可计算出该悬索人行桥在单人移动荷载和人群移动荷载作用下的竖向荷载计算工况:
| $\left\{ \begin{array}{l} {F_v}\left( t \right) = 252\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right)\;\;\;\;\;\;\;\;\;\;\left( 工况一 \right), \\ {F_{nv}}\left( t \right) = 4\;032\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right)\;\;\;\;\;\;\left( 工况二 \right), \\ {F_{nv}}\left( t \right) = 10\;836\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right)\;\;\;\;\left( 工况三 \right), \\ {F_{nv}}\left( t \right) = 38\;052\sin \left( {2{\rm{ \mathsf{ π} }}{\mathit{f}_0}t} \right)\;\;\;\;\left( 工况四 \right). \end{array} \right. $ | (12) |
当人在桥梁上行走时,桥梁按照人行走的频率进行受迫振动;当人通过桥梁后,桥梁按照自身振动频率进行自由振动.经计算,该人行桥在单人和较少行人荷载模式下(工况一、工况二)跨中峰值加速度响应小于人体舒适度限值要求,且峰值位移响应亦满足规范限值要求(人行桥跨中峰值位移限值取为l/1 000= 180 mm,l为人行桥主跨跨度);当桥上行人密度较大时(超过1.0人/m2),跨中竖向振动加速度和位移响应不满足规范要求:工况三跨中节点476的峰值加速度响应为0.68 m/s2,超过一般人群移动荷载作用下的桥面竖向振动舒适度限值0.5 m/s2的要求;工况四跨中节点476的峰值加速度响应为1.275 m/s2,超过极端密集人群荷载作用引起的桥面竖向振动加速度限值0.78 m/s2.此外,工况三、工况四跨中节点476的峰值位移分别为89.1 mm和167.1 mm,满足人行桥跨中峰值位移限值180 mm的要求.因此,拟采用调频质量阻尼器TMD对该人行桥实施竖向减振控制,以期达到符合行人振动舒适度和安全性的限值要求.
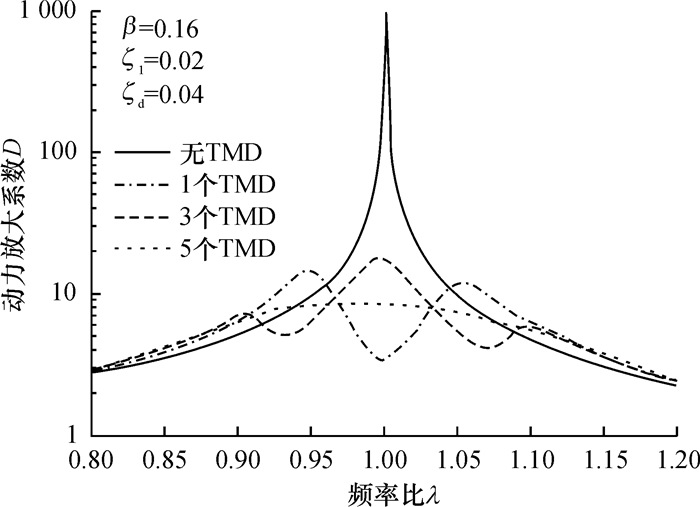
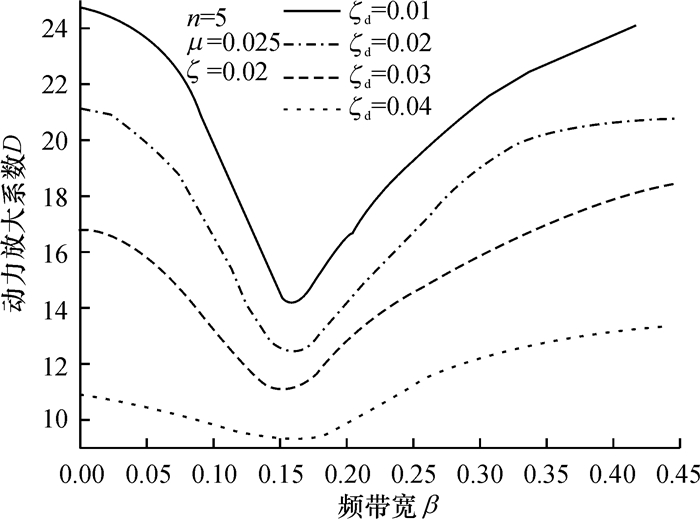
3.2 MTMD参数影响分析对于控制第一振型振动的结构而言,将TMD设置在振幅最大位置将能够达到最优的减振效果,由此本文将MTMD布置在悬索桥的跨中附近.为便于加工与设计,将各个TMD的质量系统和阻尼系统固定,通过调整刚度系统来控制MTMD的频带范围,并假定各个TMD系统的频率在频带范围内均匀分布,将桥梁结构基本自振频率定为MTMD系统的中心频率,定义频带宽β=γn-γ1.图 2、图 3显示了悬索桥动力放大系数与频率比和频带宽之间的关系.可见桥梁-MTMD体系的动力放大系数随TMD附加阻尼比的增大而逐渐减小,当采用5个TMD、频带宽取0.16时,桥梁-MTMD体系的动力放大系数最小,且能够保持在较宽的频率范围内(0.9≤λ≤1.1)具有良好稳定的动力放大系数.因此后文研究均取5个TMD组成MTMD开展桥梁减振控制研究.
|
图 2 动力放大系数D与频率比λ之间的关系 Figure 2 Relationship between D and λ |
|
图 3 动力放大系数D与频带宽β之间的关系 Figure 3 Relationship between D and β |
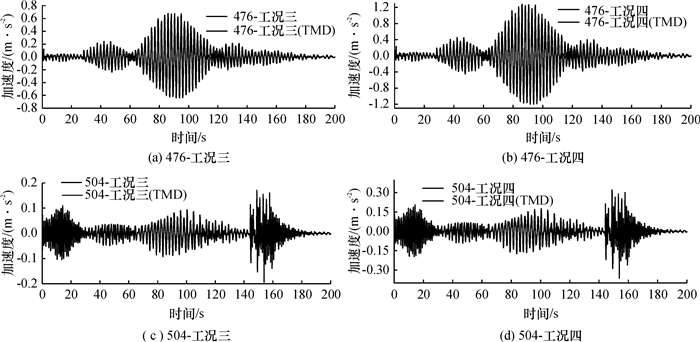
在不同行人移动荷载模式作用下,设置MTMD系统后悬索桥主跨和边跨不同节点竖向振动加速度和位移峰值响应及其减振效果见表 1,主跨和边跨跨中节点竖向振动加速度响应时程对比曲线如图 4所示.由图 4、表 1可知,行人移动荷载模式对桥梁结构的振动响应具有一定的影响,同步频人数越多,振动响应越大,越容易产生桥梁共振现象;设置MTMD系统后,悬索桥在行人移动荷载作用下(工况三和工况四),其主跨和边跨各节点的加速度响应大幅下降,平均减振效果达50%以上,且悬索桥主跨和边跨跨中峰值加速度值在一般行人移动荷载和极端密集行人作用下分别小于0.5 m/s2和0.78 m/s2,满足人体舒适度的设计要求;桥梁主跨在安装MTMD系统后,位移响应亦有较大幅度的衰减,大大提高了悬索桥的安全性.由此可见,通过在悬索桥主跨下部设置MTMD系统,有效抑制了悬索桥主跨和边跨在人群移动荷载下的振动响应,并使之在人群荷载作用下满足舒适性和安全性设计要求.
|
图 4 悬索桥加速度减振效果对比 Figure 4 Contrast of vibration control effect of the bridge acceleration responses |
| 表 1 不同工况下悬索桥峰值振动响应 Table 1 Peak responses of the suspension bridge in different cases |
本文针对大跨悬索桥结构采用MTMD系统对其进行了行人移动荷载作用下的振动控制分析,得到如下结论:
1) 行人移动荷载作用下MTMD系统对于抑制大跨悬索桥的振动响应具有良好的效果,有效提高了大跨悬索桥的舒适性和安全性;
2) 经合理设计,MTMD系统能够在较宽频率范围内有效、稳定地控制悬索桥的振动响应,可保证桥梁结构由于施工或使用不当引起实际频率与设计频率产生偏差时仍具有良好的减振效果,同时可实现多模态控制;
3) 行人移动荷载模式对桥梁结构的振动响应具有一定的影响,同步频人数越多,振动响应越大,越容易产生桥梁共振现象,宜控制桥梁振动响应控制频率在行人步频范围以外.
| [1] |
Yun C B, Lee J J, Koo K Y. Smart structure technologies for civil infrastructures in Korea: recent research and applications[J].
Structure and Infrastructure Engineering, 2011, 7(9): 673-688.
DOI: 10.1080/15732470902720109. |
| [2] |
Hoang N, Fujino Y, Warnitchai P. Optimal tuned mass damper for seismic applications and practical design formulas[J].
Engineering Structures, 2008, 30(3): 707-715.
DOI: 10.1016/j.engstruct.2007.05.007. |
| [3] |
Lee C L, Chen Y T, Chung L L, et al. Optimal design theories and applications of tuned mass dampers[J].
Engineering Structures, 2006, 28(1): 43-53.
DOI: 10.1016/j.engstruct.2005.06.023. |
| [4] |
Chung L L, Wu L Y, Huang H H, et al. Optimal design theories of tuned mass dampers with nonlinear viscous damping[J].
Earthquake Engineering and Engineering Vibration, 2009, 8(4): 547-560.
DOI: 10.1007/s11803-009-9115-3. |
| [5] |
Chung L L, Wu L Y, Yang C S W, et al. Optimal design formulas for viscous tuned mass dampers in wind-excited structures[J].
Structural Control and Health Monitoring, 2013, 20(3): 320-336.
DOI: 10.1002/stc.v20.3. |
| [6] |
张旭升, 王肇民. 钢结构电视塔的MTMD风振控制研究及设计[J].
计算力学学报, 1998, 15(1): 101-107.
Zhang X S, Wang Z M. Study and design of MTMD wind vibration control of TV tower structures[J]. Chinese Journal of Computational Mechanics, 1998, 15(1): 101-107. |
| [7] |
霍林生, 李宏男. 大跨人行过街天桥利用MTMD减振控制的理论分析[J].
防灾减灾工程学报, 2008, 28(3): 298-301.
Huo L S, Li H N. Theoretical analysis of vibration control of large-span pedestrian bridge by use of MTMD[J]. Journal of Disaster Prevent and Mitigation Engineering, 2008, 28(3): 298-301. |
| [8] |
万信华. 斜拉桥车桥耦合振动及其MTMD振动控制[D]. 武汉: 华中科技大学土木工程与力学学院, 2006.
http://cdmd.cnki.com.cn/Article/CDMD-10487-2008024169.htm
|
| [9] |
余钱华, 胡世德, 范立础. 桥梁结构MTMD被动控制的理论研究和实桥分析[J].
世界地震工程, 2001, 17(3): 105-108.
Yu Q H, Hu S D, Fan L C. Theoretical researches and real bridge analysis of Passive control of bridge structures with MTMD[J]. World Information on Earthquake Engineering, 2001, 17(3): 105-108. |
| [10] |
禹智涛, 韩大建. 基于可靠度的桥梁结构优化设计[J].
广东工业大学学报, 2002, 19(3): 50-55.
Yu Z T, Han D J. Optimal design of bridge structures based on reliability[J]. Journal of Guangdong University of Technology, 2002, 19(3): 50-55. |
| [11] |
胡利平, 韩大建, 禹智涛. 基于环境激励的大跨度桥梁模态试验[J].
广东工业大学学报, 2005, 22(1): 100-105.
Hu L P, Han D J, Yu Z T. Modal test of long span bridges based on ambient excitation[J]. Journal of Guangdong University of Technology, 2005, 22(1): 100-105. |
| [12] |
孙利民, 闫兴非. 人行桥人行激励振动及设计方法[J].
同济大学学报:自然科学版, 2004, 32(8): 996-999.
Sun L M, Yan X F. Human walking induced footbridge vibration and its serviceability design[J]. Journal of Tongji University:Natural Science, 2004, 32(8): 996-999. |
| [13] |
Mstsumoto Y, Nishioka T, Shiojiri H. Study on dynamic design of pedestrian over-bridges in consideration of characteristics of pedestrians[J].
Proc JSCE, 1972, 9(205): 63-70.
|
| [14] |
Fujino Y, Pacheo B M, Nakamura S, et al. Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge[J].
Earthquake Engineering and Structural Dynamics, 1993, 22(9): 741-758.
DOI: 10.1002/(ISSN)1096-9845. |
| [15] |
British Standard 5400. Steel, concrete and composite bridges: Specification for loads[S]. Britain: British Standards Institution, 1978.
|
 2014, Vol. 31
2014, Vol. 31

