目前国内外关于羽毛球研究的文献还比较少[1-14],这些文献研究主要是把羽毛球当作一个质点来讨论其飞行轨迹;有些学者还研究天然羽毛片组装的羽毛球与塑料羽毛片组装的羽毛球之间的空气阻力系数和雷诺系数的区别.然而关于羽毛球组成要素的研究还比较少.羽毛球主要由球托和羽毛片组成,球托是比较规则的物体,容易研究;羽毛片的杆端插在球托上,其叶顶端围成圆形,直径比球托直径大2倍.羽毛片不是直线型的, 而是具有一定的弯拱度,不同弯拱度的羽毛片插在球托上会影响整个羽毛球的动态稳定性.羽毛球的动态稳定性主要表现在羽毛球飞行旋转过程中有无摆动以及落点是否准确.选择什么类型的羽毛片插在球托上才能使得羽毛球具有最好的动态稳定性是组装羽毛球的关键问题,这里不仅涉及到羽毛片弯拱度级数的选取,还涉及到羽毛片攻角以及安装角的选取,这些不同因素的组合都会引起整个羽毛球在飞行旋转过程当中产生不同的动态不平衡,从而导致羽毛球在飞行旋转过程中产生不同的摆动、落点偏离, 影响羽毛球整个飞行过程的气动特性,甚至还影响羽毛球的质量品质.因此,研究有关羽毛片要素对羽毛球动态稳定的影响是非常必要的.
关于羽毛片要素引起羽毛球动态不平衡的原因还没有查到相关文献报道.国内某工厂在如何选取羽毛片型号方面都是根据自己长期积累的一些经验总结,并没有给出相关理论解释,然后利用羽毛球风洞实验装置反复调节羽毛球动态平衡,由于羽毛球的动态平衡调节不像一般的转子调节那样增加或减小某个位置的质量即可,而是通过调节安装角或者对换某个位置的羽毛片等方式,使得羽毛球动态平衡符合一定的要求.
同一个球托插入羽毛片数目不同,对整个羽毛球的动态稳定影响也是不一样.目前来说,一般球托是插16根羽毛片,然而对于给定插入数目的球托,用不同类型羽毛片组装或者给定同一类型的16片羽毛片用不同顺序方式插入,对羽毛球动态稳定性影响也各异.羽毛片对羽毛球动态不稳定的影响主要分为两种,一是球托或羽毛片的质量不平衡引起的羽毛球动态不稳定, 另外就是羽毛片气动力不平衡引起的羽毛球动态不稳定.本文主要考虑羽毛片对羽毛球气动力影响问题,通过建立羽毛片气动力模型,并对模型进行理论分析,寻找羽毛片的相关要素比如弯拱度、攻角以及安装角对羽毛球气动力的影响, 最后利用实验进行验证.
1 羽毛片要素对羽毛球飞行旋转的影响羽毛球组装是用16片羽毛片固定在球托上的,羽毛片排列情况是以球托的中心对称点为圆心,半径为R(R是大于零小于球托半径)的圆周边上,先定好攻角大小,并任取圆周上一点作为起始插入点,然后绕着圆心按顺时针(或逆时针)旋转,每旋转22.5°就插入一根羽毛片.由于羽毛球的特殊性,16片羽毛片可以看作是任意8片羽毛片绕着球托圆心旋转180°得到剩下的8片羽毛片位置.绕着球托圆心中心对称后得到的两片羽毛片,其叶面开口方向刚好是相反的.因此,研究空气作用在羽毛球上的气动力,暂时忽略空气对球托气动力影响,只需研究羽毛球上绕着球托圆心中心对称后得到的两片羽毛片的气动力即可,剩下的14片羽毛片可以类似分析.
空气作用在羽毛片上的气动力与空气作用在羽毛球上的压力中心位置有关.羽毛片的位置、攻角、安装角或者长度等的改变都会引起羽毛球的压力中心位置发生改变,从而导致其对应的气动力作用点也发生改变.设羽毛球以速度v打出,根据作用力与反作用力的关系,相当于风以风速v作用在羽毛球上,由于空气的黏性作用,风会对羽毛球产生气动力作用.羽毛片的顶端围成圆形,其圆形直径比球托直径大2倍,因此羽毛片所围成的表面积要比球托所围成的表面积大.当羽毛球向前飞行旋转前进时,羽毛片所围成的表面向外推开空气的量要比球托的多,根据伯努利原理可知,空气作用在羽毛球上的压力中心应该在羽毛片附近,相对来说比较靠后的地方.由此可得,羽毛片要素的改变会影响空气作用在羽毛球上的气动性能,从而影响羽毛球飞行旋转的动态稳定性.
2 羽毛片气动力模型对组装好的羽毛球,一般都要求其在飞行过程中受到空气作用时能够绕着其对称轴旋转,目的就是要克服因组装等过程中导致的气动力偏心或质量不平衡,以保证羽毛球飞行旋转稳定,落点准确.当羽毛球以一定攻角飞行旋转时,空气流对前进飞行的羽毛球产生阻力作用.空气阻力大小与羽毛球扫晾过的面积以及飞行速度等有关,而羽毛球扫晾过的面积大小与羽毛片的攻角以及长短等有关.此外,羽毛球飞行旋转过程中会与周围空气相互摩擦而形成环流,在空气流和环流的共同作用下,与气流同向的羽毛球一侧空气流速加快;反之,则越慢.根据伯努利原理,空气流速加快的羽毛球一侧压力下降,空气流速减小的羽毛球一侧压力变大,上下两侧的压力差对羽毛球产生一个压差阻力.即球托圆心中心对称的上下两片羽毛片除了受到空气阻力外还受到压差阻力作用,这些气动力的合力影响羽毛球动态稳定.为了便于研究,如图 1所示,设第i片羽毛片对应的攻角为αi,并以安装角度δi与球托固定.羽毛球以速度v飞行旋转,其绕着对称轴旋转的角速度设为ω,上下关于球托圆心中心对称的两片羽毛片在羽毛球飞行旋转过程中的实际迎角设为α11和α22,则有如下的关系式:

|
图 1 羽毛球实物图及羽毛片气动力分析图 Figure 1 Badminton physical figure and feather aerodynamic analysis diagram |
上方羽毛片的实际迎风角为
| ${\alpha _{11}} = {\alpha _1} - {\mathit{\delta }_{\rm{1}}} + \arcsin \frac{{\omega {r_1}}}{v}; $ |
下方羽毛片的实际迎风角为
| ${\alpha _{22}} = {\alpha _2} + {\mathit{\delta }_{\rm{2}}} - \arcsin \frac{{\omega {r_2}}}{v}. $ |
其中,α1, δ1, r1为上片羽毛片对应的攻角、安装角以及上羽毛片到旋转轴的距离;α2, δ2, r2为下片羽毛片对应的攻角、安装角以及下羽毛片到旋转轴的距离.
空气作用在羽毛球上所有气动力的合力可以分解为沿着羽毛杆方向上的力和垂直羽毛叶面上的法向力.沿着羽毛杆方向上的力只会对杆起作用,一般的羽毛杆都会用胶水等固定在球托上,所以不考虑作用在羽毛杆上的力的影响,只考虑作用在羽毛叶面上的法向力.设上下关于球托圆心中心对称的两片羽毛片受到空气作用产生气动合力的法向力为N1和N2,它们分别垂直各片羽毛叶面且方向相反.由于两片羽毛叶面在对称旋转轴一侧,把作用在羽毛叶面上的气动法向力N1和N2沿着旋转轴方向和垂直旋转轴方向上投影,则上片羽毛叶面的法向力N1在平行旋转轴方向上投影为N1sinδ1,在垂直旋转轴方向上投影为N1cosδ1;下片羽毛叶面的法向力N2在平行旋转轴方向上投影为-N2sinδ2,在垂直旋转轴方向上投影为-N2cosδ2.其中,负号表示方向相反.设投影力N1cosδ1对应的羽毛叶面压力中心到旋转轴的距离为r3,投影力N2cosδ2对应的羽毛叶面压力中心到旋转轴的距离为r4,则上下两片羽毛片在垂直旋转轴方向提供的气动合力的力矩为N1r3cosδ1-N2r4cosδ2.
2.1 气动力矩的计算羽毛叶面的参考平均叶面宽度设为l,羽毛片的直线型长度设为L,且羽毛叶面为规则图形,羽毛叶面对应的法向力系数设为c1,羽毛杆的长度设为p,羽毛叶面的压力中心位置为
| $\begin{array}{l} {N_1}{r_3} = \frac{1}{2}{r_3}\int_{p1}^{{L_1}} {\mathit{\rho }{\mathit{v}^{\rm{2}}}{c_1}\left( {{\mathit{\alpha }_{\rm{1}}} - {\mathit{\delta }_{\rm{1}}} + \arcsin \frac{{\omega {r_1}}}{v}} \right)} l\left( {{p_1} + \frac{3}{4}r} \right)r{\rm{d}}r;\\ {N_2}{r_4} = \frac{1}{2}{r_4}\int_{p2}^{{L_2}} {\rho {v^2}{c_1}\left( {{\mathit{\alpha }_{\rm{2}}} + {\mathit{\delta }_{\rm{2}}} - \arcsin \frac{{\omega {r_2}}}{v}} \right)} l\left( {{p_2} + \frac{3}{4}r} \right)r{\rm{d}}r. \end{array} $ | (1) |
若上下两片羽毛片要素是一样的,则它们对应的羽毛叶面压力中心点到旋转轴的距离r3=r4且α1=α2,δ1=δ2,p1=p2,L1=L2.由式(1)得,上下两片羽毛片在垂直旋转轴方向提供的气动合力的力矩为
| $M = - \frac{1}{2}{r_3}\mathit{\rho l}{\mathit{v}^2}{\mathit{c}_1}\left( { - {\delta _1} + \arcsin \frac{{\omega {L_1}\sin {\mathit{\alpha }_{\rm{1}}}}}{v}} \right) \times \left( {{p_1}L_1^2 + \frac{1}{2}L_1^3 - \frac{3}{{20}}p_1^3} \right)\cos {\mathit{\delta }_1}. $ | (2) |
若上下两片羽毛片要素是不一样的,则它们对应的羽毛叶面压力中心点到旋转轴的距离r3≠r4且α1≠α2,δ1≠δ2,p1≠p2,L1≠L2.由式(1)得,上下两片羽毛片在平行旋转轴方向提供的气动合力的力矩为
| $\begin{array}{*{20}{l}} {M' = \frac{1}{2}{r_3}\rho l{v^{\rm{2}}}{c_1}\left( {{\alpha _1} - {\delta _{\rm{1}}} + \arcsin \frac{{\omega {L_1}\sin {\alpha _{\rm{1}}}}}{v}} \right) \times }\\ {\left( {\frac{1}{2}{p_1}L_1^2 + \frac{1}{4}L_1^3 - \frac{3}{4}p_1^3} \right)\cos {\delta _{\rm{1}}} - \frac{1}{2}{r_4}\rho l{v^{\rm{2}}}{c_1}\left( {{\alpha _{\rm{2}}} - {\delta _{\rm{2}}} + \arcsin \frac{{\omega {L_2}\sin {\alpha _2}}}{v}} \right)}\\ {\left( {\frac{1}{2}{p_2}L_2^2 + \frac{1}{4}L_2^3 - \frac{3}{4}p_2^3} \right)\cos {\delta _{\rm{2}}}.} \end{array} $ | (3) |
其中,p1, L1为上片羽毛片对应的羽毛杆的长度以及上片羽毛片的直线型长度;p2, L2为下片羽毛片对应的羽毛杆的长度以及下片羽毛片的直线型长度.
另外,羽毛片是具有弯拱度的,弯拱度会缩短羽毛片的直线型长度,根据实验测量并归纳总结,得到具有弯拱度羽毛片的总长度与直线型长度的关系式
| ${L_i} = {h_i} = {d_i} - 0.01\left( {{n_i} + {m_i}} \right). $ | (4) |
其中,di为具有弯拱度第i羽毛片的总长度,ni为第i羽毛片对应的弯度级数,mi为第i羽毛片对应的拱度级数.
把式(4)代入式(2),得到上下两片羽毛片在垂直旋转轴方向的气动合力的力矩为
| $M = - \frac{1}{2}{r_3}\rho l{v^2}{c_1}\left( { - {\mathit{\delta }_{\rm{1}}} + \arcsin \frac{{\omega {h_1}\sin {\mathit{\alpha }_{\rm{1}}}}}{v}} \right)\left( {{p_1}h_1^2 + \frac{1}{2}h_1^3 - \frac{3}{2}p_1^3} \right)\cos {\mathit{\delta }_{\rm{1}}}. $ | (5) |
影响羽毛球动态稳定性的主要是空气作用在羽毛球上的气动力在垂直旋转轴方向上的分力矩.要使得羽毛球在飞行旋转过程中保持动态稳定,只有气动力在羽毛球旋转轴垂直方向上的分力矩为零,才能够保证羽毛球不产生摆动或晃动现象.即M=0.根据式(5)可知,需安装角δ1为90°,或
(1) 若安装角度为90°时,16片羽毛片变成4对十字型的形式插在球托上,羽毛叶面的开口方向与空气流方向平行,空气作用在羽毛叶面上的气动力为零.此种情形不符合羽毛球设计要求,也不利于羽毛球飞行旋转.
(2) 若
(3) 若
因此,当羽毛片的安装角与羽毛球的转速、飞行初始速度、羽毛片的攻角、羽毛片的弯拱度以及羽毛片的长度满足上述3个条件时,羽毛球飞行旋转的动态稳定性是最好的.
按照上述方法,也可以对式(3)所在情形进行分析,得到类似的结果.同样,剩下其它的羽毛片也可以类似上述方法进行分析讨论, 在此就不再赘述.
3 实验结果与仿真结果讨论羽毛球如图 1所示,利用某工厂提供的羽毛球风洞实验装置[15],对插好羽毛片的羽毛球,通过寻找羽毛片安装角与羽毛片的攻角、羽毛球飞行速度以及羽毛片长度等要素之间的关系式,使得羽毛球飞行旋转满足动态稳定,并把实验所得结果与仿真结果对比,结果表明实验所得结果略大于仿真值.定量分析羽毛片要素发现,实验所得结果与仿真结果误差不大.
3.1 速度与安装角的关系当16片羽毛片长度都为0.075 m,攻角为20°,其对应的弯拱度都为一样,旋转角速度为80 r/s时,利用羽毛球风洞实验装置,通过改变风洞风速度,寻找羽毛片安装角,使得羽毛球满足飞行旋转动态稳定.如图 2所示.
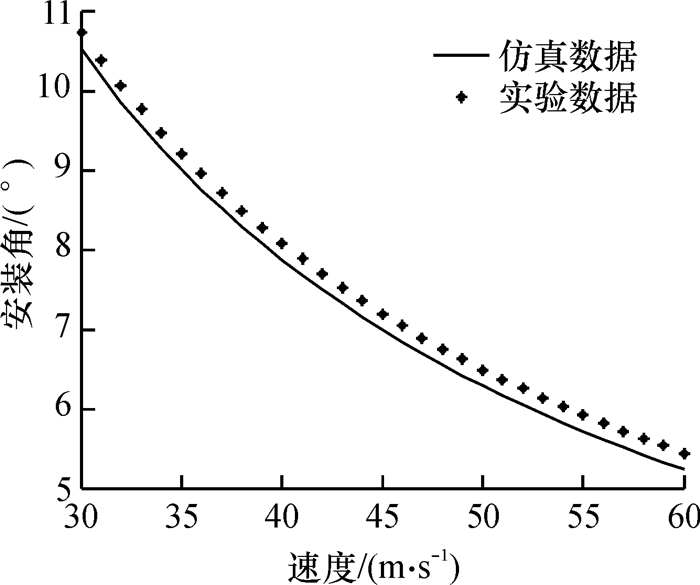
|
图 2 速度变化与安装角的关系 Figure 2 Speed change and the installation angle |
由图 2可知,随着风速不断增加,羽毛片安装角由大变小,主要是随着风速的不断加大,空气作用在羽毛片上的气动力也不断增大,在其他参数不变的情况下,只有调节安装角才可以保证空气作用在旋转轴垂直方向上的气动力的分力矩为零.实验所得结果略比仿真结果大,这是因为在实验中存在一定的人为因素误差,这些是可以接受的.
3.2 攻角与安装角的关系当羽毛球旋转角速度为80 r/s,16片羽毛片长度都为0.075 m,其对应的弯拱度都为一样,风速为50 m/s时,利用羽毛球风洞实验装置,通过改变羽毛片的攻角大小,寻找羽毛片安装角,使得羽毛球满足飞行旋转动态稳定.如图 3所示.
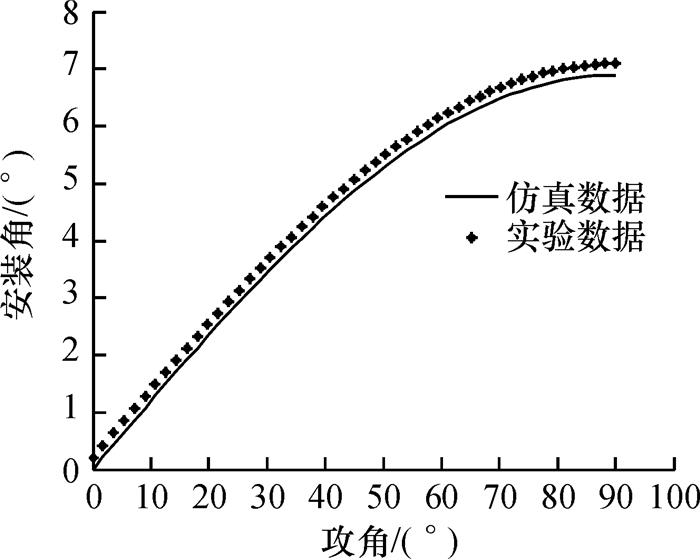
|
图 3 攻角变化与安装角的关系 Figure 3 Relationship between the change in attack angle and installation angle |
由图 3可知,随着羽毛片的攻角不断增大,羽毛片安装角也随之不断增大.这是因为在其他因素不变时,随着攻角从0°开始不断增大,羽毛球的旋转半径不断增加,因而导致作用在羽毛片上的气动力的合力矩增大,要想保证气动力在垂直旋转轴方向上的分力矩为零,安装角必须不断增大,实验所得数值略大于仿真结果.
3.3 长度与安装角的关系当16片羽毛片的攻角都为20°,其对应的弯拱度都为一样,羽毛球旋转角速度为80 r/s,风速为50 m/s时,用羽毛球风洞实验装置,通过改变羽毛片长度,寻找羽毛片安装角,使得羽毛球满足飞行旋转动态稳定.如图 4所示.
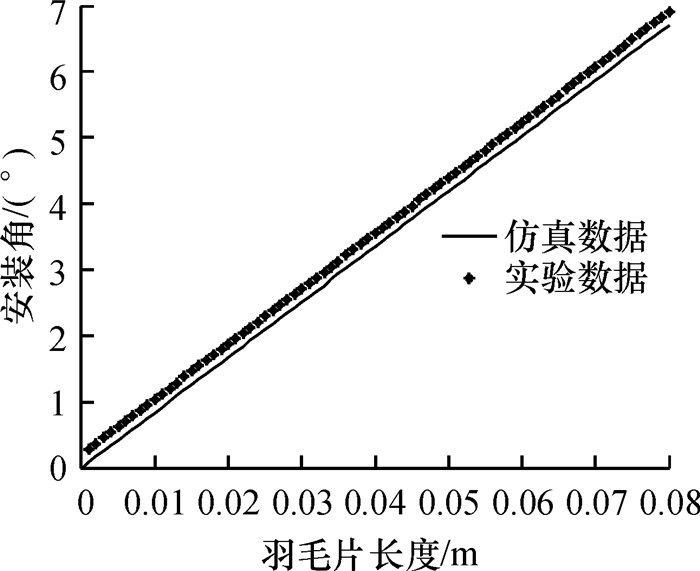
|
图 4 羽毛片长度与安装角的关系 Figure 4 Feather piece length and installation angle |
由图 4可知,随着羽毛片长度不断增大,羽毛片安装角也是跟着不断增大的.因为随着羽毛片长度不断增加,空气作用在羽毛片上的气动力也随之不断增加,因而要保证羽毛球飞行旋转稳定,必须增加羽毛片的安装角才能够保证在气动力在垂直旋转轴方向上的分力矩为零,实验所反映的结果与仿真结果是一致的.
3.4 角速度与安装角的关系当16片羽毛片的攻角都为20°,其对应长度都为0.075 m,对应的弯拱度都为一样,风速为50 m/s时,用羽毛球风洞实验装置,通过改变羽毛球旋转角速度,寻找羽毛片安装角,使得羽毛球满足飞行旋转动态稳定.如图 5所示.
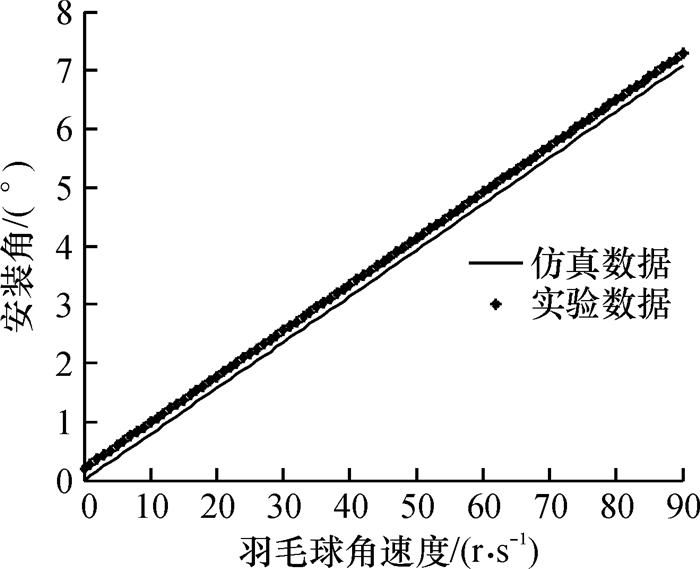
|
图 5 角速度与安装角的关系 Figure 5 Change in angular velocity and installation angle |
由图 5可知,随着羽毛球旋转角速度不断增加,羽毛片安装角也是不断增加的.因为随着羽毛球旋转角速度不断增加,空气作用在羽毛片上的气动力也不断增加,因而要保证羽毛球飞行旋转稳定,必须增加羽毛片的安装角才能够保证在气动力在垂直旋转轴方向上的分力矩为零,实验所反映的结果与仿真结果是一致的,实验所得结果比仿真结果稍大.
4 结论羽毛球主要由球托和羽毛片组成,球托是比较规则的物体,易于研究;羽毛片不是直线型的而是具有弯拱度的,弯拱度不仅影响空气作用在羽毛球上的压力中心位置,还影响空气作用在羽毛球上的气动力.此外,羽毛片的攻角、安装角以及长度等要素同样影响空气作用在羽毛球上的气动力,而且还影响羽毛球飞行旋转的动态稳定性以及落点准确性.据此,本文首先对空气作用在羽毛球上的压力中心位置进行分析,分析表明羽毛片要素的改变影响压力中心位置的变化,从而影响空气作用在羽毛球上的气动力.其次,通过建立羽毛片气动力模型,分析关于球托圆心中心对称的上下两片羽毛片,结合流体力学的气动力特性知识,并利用实验数据拟合得到的一些有关羽毛片要素的经验公式.如具有弯拱度羽毛片的直线型长度经验公式,得到羽毛片要素对羽毛球飞行旋转影响的公式.根据羽毛球动态稳定性的要求,讨论了羽毛片安装角与其攻角、长度以及羽毛球飞行速度等之间的关系,从而得到满足羽毛球动态稳定性要求的有关羽毛片要素的计算公式.实验结果与仿真结果对比表明,虽然实验所得到的结果略大于仿真结果,但实验所反映的结果与计算结果是一致的.
| [1] |
Alam F, Chowdhury H, Theppadungporn C, et al. Measurements of aerodynamic properties of badminton shuttlecocks[J].
Procedia Engineering, 2010, 2(2): 2487-2492.
DOI: 10.1016/j.proeng.2010.04.020. |
| [2] |
Kitta S, Hasegawa H, Murakami M, et al. Aerodynamic properties of a shuttlecock with spin at high Reynolds number[J].
Asia-Pacific Congress on Sports Technology, 2011(13): 271-277.
|
| [3] |
Personnic J L, Alam F, Gendre L L, et al. Flight trajectory simulation of badminton shuttlecocks[J].
Asia-Pacific Congress on Sports Technology, 2011(13): 344-349.
|
| [4] |
艾星芳, 汪仁煌, 李雪晨. 圆度误差测量在羽毛球外观检测中的应用[J].
广东工业大学学报, 2011, 12(4): 51-54.
Ai X F, Wang R H, Li X C. The application of roundness error measurement in the detection of badminton appearance[J]. Journal of Guangdong University of Technology, 2011, 12(4): 51-54. |
| [5] |
Nakagawa K, Hasegawa H, Murakami M, et al. Aerodynamic properties and flow behavior for a badminton shuttlecock with spin at high reynolds numbers[J].
Procedia Engineering, 2012(34): 104-109.
|
| [6] |
谷嘉锦, 陈玉清. 羽毛球风洞的设计与应用[J].
实验力学, 1980, 9(3): 227-231.
Gu J J, Chen Y Q. The design and application of badminton wind tunnel[J]. Journal of Experimental Mechanics, 1980, 9(3): 227-231. |
| [7] |
Chen B Q, Wang Z Q. A statistical method for analysis of technical data of a badminton match based on 2-D seriate images[J].
Tsinghua Science & Technology, 2007, 12(5): 594-601.
|
| [8] |
Chen L M, Pan Y H, Chen Y J. A study of shuttlecock's trajectory in badminton[J].
Journal of Sports Science and Medicine, 2009, 77(8): 657-662.
|
| [9] |
Paramesran R, Teng S L. Detection of service activity in a badminton game[J].
IEEE Region 10 Annual International Conference, Proceedings/TENCON, 2011: 312-315.
|
| [10] |
Fumito Y, Takumi K, Kenji W, et al. Automated service scene detection for badminton game analysis using CHLAC and MRA[J].
World Academy of Science, Engineering and Technology, 2010(62): 942-945.
|
| [11] |
张晶华, 汪仁煌, 岳洪伟. 具有弯拱度羽毛片的特性及其应用[J].
广东工业大学学报, 2013, 30(3): 58-64.
Zhang J H, Wang R H, Yue H W. On the characteristics of curved camber feathers and the application[J]. Journal of Guangdong University of Technology, 2013, 30(3): 58-64. |
| [12] |
Chan C M, Rossmann J S. Badminton shuttlecock aerodynamics: synthesizing experiment and theory[J].
Sports Engineering, 2012, 15(2): 61-71.
DOI: 10.1007/s12283-012-0086-7. |
| [13] |
张晶华, 汪仁煌, 岳洪伟. 毛片空气动力学几何参数分析与仿真[J].
科学技术与工程, 2013, 13(23): 101-107.
Zhang J H, Wang R H, Yue H W. Feather aerodynamics geometric parameter analysis and simulation[J]. Science Technology and Engineering, 2013, 13(23): 101-107. |
| [14] |
林传潮. 羽毛球空气力学分析[J].
中国体育科技, 1980(13): 27-33.
Lin C C. The analysis of badminton aerodynamics[J]. China Sport Science and Technology, 1980(13): 27-33. |
| [15] |
李逸岳. 形状图像检测技术研究与应用[D]. 广州: 广东工业大学自动化学院, 2013.
|
 2014, Vol. 31
2014, Vol. 31

