2. 广东工业大学 管理学院, 广东 广州 510520
2. School of Management, Guangdong University of Technology, Guangzhou 510520, China
社会网络是指一组已经或有可能(直接或间接)连接的“点”(个人或团体)以及“点”之间的关系构成的集合[1-2].而社会网络分析就是包括测量与调查社会系统中各部分(“点”)的特征与相互之间的关系(“连接”),将其用网络的形式表示出来,然后分析其关系的模式与特征这一全过程的一套理论、方法和技术[3].社会网络分析是在伟大的人类学家拉德克利夫-布朗(Radcliffe-Brown)对结构的关切之中,以一种相对非技术化的形式化出现的[4].
对社会网络的研究,已有很多成果[1-10].从这些文献可以看出,在理论研究方面,社会网络领域是以理论引入为特征的,主要是从包括数学和社会心理学在内的其他学科借鉴有关的理论,并作了更改和拓展;异质性理论和结构角色理论可以成为本源的社会网络理论;已有相当可观的网络思想被现有的组织理论所吸收[5].在方法研究方面,社会网络方法有可能帮助人们理解个体行动者是如何构建、维持和利用社会结构,并受到社会结构的约束的,因此有时也被称为“结构分析”.然而,导致社会网络研究者忽视微观—宏观链接和网络动态问题的原因,除了对技术问题的过度关注,还在于网络研究中存在的一个基本导向,即只研究静态社会结构,忽视具有能动性的个体行动者的作用[5].另外,研究网络结构的学者往往置行动者的属性于不顾,只注重对关系结构的分析和描述,这些都是导致研究结论与实际脱节的重要原因.
可拓学是中国人创立的新学科,经过多年的努力,可拓学研究工作经历了概念与思想的提出、基础理论框架的建立为主的两个阶段.目前,开始进入应用研究和理论研究相结合的阶段[11].它以基元为逻辑细胞,通过对事、物、关系的形式化研究,建立了物元、事元、关系元、复合元、可拓集等概念,进而建立了信息-知识-策略形式化体系、拓展分析方法、共轭分析方法、可拓变换方法和优度评价方法等,利用可拓集合和关联函数作为定量化工具,探讨了矛盾问题求解策略的生成等[12-15].目前,可拓学的理论框架和方法体系已初步形成,并成功应用于决策与策略生成、产品构思与设计、数据挖掘、知识工程与知识管理、控制与检测等[11, 16-21].
本文将可拓论与可拓创新方法应用于社会网络结构研究,首先把社会网络构造成基元网,再利用基元的拓展分析方法,分析社会个体成员及他们之间的关系,探讨他们的可拓变换,并利用优度评价方法评价社会网络.通过应用这种新的理论与方法,可以从定性与定量相结合的角度认识社会网络,以便消除社会网络研究中结构主义与个体主义方法论之间的隔阂,为利用计算机和网络技术进行社会结构研究提供一种新的可操作方法.
1 可拓学的基本知识可拓学研究了描述现实世界中的事物和关系、信息和知识以及问题的形式化方法,建立了基元的拓展分析理论与方法、物的共轭分析理论与方法、可拓变换理论与方法、可拓集合理论与方法、优度评价方法,提出了矛盾问题转化的基本方法.可拓学为人们认识和分析现实世界、解决现实世界中的矛盾问题, 提出了一种新的方法论.下面简要介绍本文用到的一些基本知识.
1.1 基元与复合元为了形式化描述物、事和关系,建立了物元、事元和关系元的概念,它们是可拓学的逻辑细胞,统称为基元.基元记作
| $ B\left( t \right) = \left( {O\left( t \right),C,V\left( t \right)} \right) = \left[ {\begin{array}{*{20}{c}} {{\rm{Object}}\left( t \right),}&{{c_1},}&{{v_1}}\\ {}&{{c_2},}&{{v_2}}\\ {}& \vdots&\vdots \\ {}&{{c_n},}&{{v_n}\left( t \right)} \end{array}} \right]. $ |
其中O(t)(Object)表示某对象(物、动作或关系词),c1, c2, …, cn表示对象O(t)的n个特征,v1(t), v2(t), …, vn(t)表示对象O(t)关于上述特征的相应量值,t为参变量,且
| $ C = \left[ {\begin{array}{*{20}{c}} {{c_1}}\\ {{c_2}}\\ \vdots \\ {{c_n}} \end{array}} \right],V\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{v_1}\left( t \right)}\\ {{v_2}\left( t \right)}\\ \vdots \\ {{v_n}\left( t \right)} \end{array}} \right]. $ |
当t为时间参数时,称B(t)为动态基元.当不需特别指明参变量时,通常简化记为B.
对于一类对象,规定了类基元的概念:
给定一类对象{O},若对任一O∈{O},关于特征ci(i=1, 2, …, n),有vi=ci(O)∈Vi,则称基元集
| $ \left\{ B \right\} = \left[ {\begin{array}{*{20}{c}} {\left\{ O \right\},}&{{c_1},}&{{V_1}}\\ {}&{{c_2},}&{{V_2}}\\ {}& \vdots&\vdots \\ {}&{{c_n},}&{{V_n}} \end{array}} \right] = \left( {\begin{array}{*{20}{c}} {\left\{ O \right\},}&{C,}&{V} \end{array}} \right) $ |
为类基元.为方便起见,在不致引起混淆的情况下,类基元也常用B表示.
显然,类基元包括类物元、类事元和类关系元.
基元概念体现了质与量的有机结合,利用全征基元又可从整体的角度分析事物.利用基元,可以形式化表示社会网络中的各个个体成员及其之间的关系,从而形成基元网,并随着对个体成员的观察层次的不同,形成不同的社会网络.
1) 当个体成员是个人时,每个基元中的对象代表的是其中的每个人.例如,人际关系基元网表示组织中所有组成人员形成的关系网络.
2) 当个体成员是业务单位时,每个基元中的对象代表的是其中的每个业务单位.例如,组织关系基元网表示组织中所有业务部门形成的关系网络.
3) 当个体成员是组织时,每个基元中的对象代表的是其中的每个组织.例如,企业关系基元网表示众多企业形成的企业群所构成的企业关系网络.
现实世界中的问题,往往是非常复杂的,是人、事、物组合或复合的结果.因此,描述这些对象,需要使用物元、事元和关系元复合的形式来表达,统称为复合元.研究复合元的构成、运算和变换就成为研究复杂问题的基础.
1.2 拓展分析与共轭分析基元的拓展分析包括:发散分析,相关分析,蕴含分析和可扩分析.利用基元的拓展分析对社会网络进行分析,可以对社会网络中的每一个个体成员的信息进行拓展,也可以通过对个体成员的拓展分析构建社会网络,为进一步细化和丰富社会网络结构提供工具.
共轭分析是用形式化模型从4个角度对事物的整体进行的全面分析,包括:虚实共轭分析,软硬共轭分析,潜显共轭分析和负正共轭分析.研究全面认识事物的共轭分析方法,既体现了中国古代的系统观和整体论的思想,也结合了还原论的分析方法.从共轭分析的角度看社会网络,是对一个组织进行的软硬共轭分析,该组织的各个体成员是其组成部分——硬部,他们之间的关系是其软部.利用共轭分析分析社会网络中的个体成员,也会获得更加丰富的个体信息,有利于对社会网络结构的分析.
1.3 可拓变换与优度评价变换是使问题的性质发生量变或质变的工具.从变换的对象考虑,可拓变换包括研究对象所形成的论域的变换、衡量对象的性质的关联准则的变换、论域中的对象的变换.从变换的形式考虑,可拓变换包括基本变换、变换的运算、变换的复合等[11].
对社会网络中的个体成员实施某个变换,可能会发生很多传导变换,需要研究变换对社会网络的影响、作用和效果等.另外,随着接受主动变换的个体成员在网络中的地位不同,所发生的传导变换也不相同,有些可能是量变,有些可能是质变.
优度评价法是评价研究对象优劣的一种有效方法,包括单特征评价、多特征评价、单级评价和多级评价等[13].优度评价法可以用于对社会网络中的个体成员具有某种性质的程度进行评价,也可用于综合衡量社会网络的优劣.
2 社会网络的基元网表示方法 2.1 个体成员形成的物元网设社会个体成员用Oi表示,物元Mi表示Oi关于特征c1, c2, …, cn的量值为v1, v2, …, vn:
| $ {M_i} = \left( {{O_i},C,V} \right) = \left[ {\begin{array}{*{20}{c}} {{O_i},}&{{c_1},}&{{v_{1i}}}\\ {}&{{c_2},}&{{v_{2i}}}\\ {}& \vdots&\vdots \\ {}&{{c_n},}&{{v_{ni}}} \end{array}} \right], $ |
则社会网络可表示为由物元Mi构成的物元网(注:当需要讨论社会网络的动态性时,要用动态物元Mi(t)构成的动态物元网表示).
例如,设O为某个学生张明,则用如下物元可以形式化表示出张明的信息:
| $ M = \left[ {\begin{array}{*{20}{c}} {张明,}&{性别,}&{男}\\ {}&{年龄,}&{20岁}\\ {}&{年级,}&{大二}\\ {}&{籍贯,}&{广东}\\ {}&{性格,}&{外向}\\ {}&{业余爱好,}&{打篮球} \end{array}} \right]. $ |
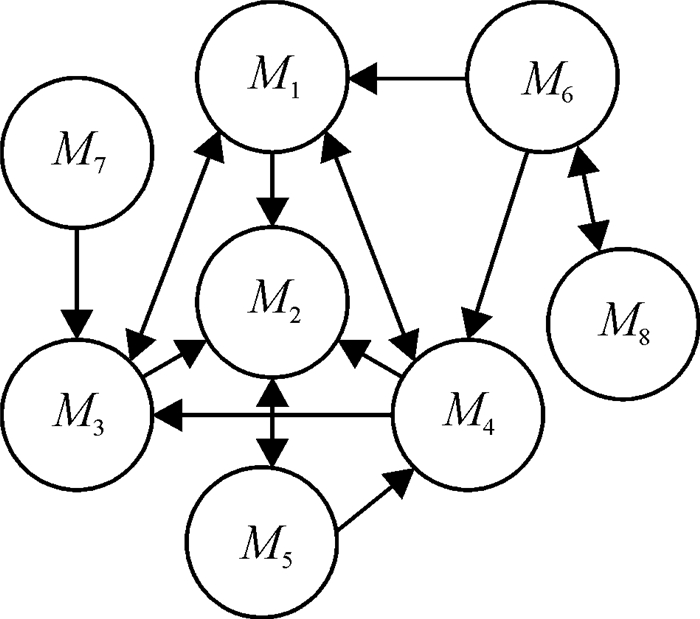
图 1为由8个物元构成的物元网.
|
图 1 物元网 Figure 1 Matter-elements network |
上述物元网类似于用图论中的图表示的社会网络,但有本质的不同.图论中用点代表个体成员,不考虑个体成员的属性及其量值,在分析社会网络时,就忽略了个体的作用.图论中用点之间的连线代表个体之间的关系,包括单向关系和双向关系.物元网中也有类似的表示,如图 1中就既有单向关系又有双向关系,还可以用关系元表示.
两个物元Mi与Mj之间的关系(图 1中的连接线)用关系元Rij表示,
| $ {M_1}\left[ \begin{array}{l} \left( {{{\vec R}_{12}}} \right){M_2}\left[ \begin{array}{l} \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over R} }_{23}}} \right){M_3}\\ \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over R} }_{24}}} \right){M_4}\\ \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over R} }_{25}}} \right){M_5} \end{array} \right.\\ \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over R} }_{13}}} \right){M_3}\left[ \begin{array}{l} \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over R} }_{34}}} \right){M_4}\\ \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over R} }_{37}}} \right){M_7} \end{array} \right.\\ \left. {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over R} }_{14}}} \right){M_4}\left[ \begin{array}{l} \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over R} }_{45}}} \right){M_5}\\ \left( {\overrightarrow R _{46}} \right){M_6} \end{array} \right.\\ \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}} \over R} }_{16}}} \right){M_6}\left[ {\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over R} }_{68}}} \right){M_8}} \right.. \end{array} \right. $ |
若只研究个体成员之间的某一种关系,则关系元可省略,表示为如下形式即可:
| $ {M_1}\left[ \begin{array}{l} \left( \to \right){M_2}\left[ \begin{array}{l} \left( \leftarrow \right){M_3}\\ \left( \leftarrow \right){M_4}\\ \left( \leftrightarrow \right){M_5} \end{array} \right.\\ \left( \leftrightarrow \right){M_3}\left[ \begin{array}{l} \left( \leftarrow \right){M_4}\\ \left( \leftarrow \right){M_7} \end{array} \right.\\ \left( \leftrightarrow \right){M_4}\left[ \begin{array}{l} \left( \leftarrow \right){M_5}\\ \left( \to \right){M_6} \end{array} \right.\\ \left( \leftarrow \right){M_6}\left[ {\left( \leftrightarrow \right){M_8}} \right.. \end{array} \right. $ |
例如,5个学生Msi(i=1, 2, 3, 4, 5)和3个教师Mtj(j=1, 2, 3)形成的“师生关系”物元网:
| $ {M_{t1}}\left[ \begin{array}{l} \left. \begin{array}{l} \left( \to \right){M_{s1}}\\ \left( \to \right){M_{s2}} \end{array} \right]\left( \leftarrow \right){M_{t3}}\left( \to \right){M_{s4}}\\ \left( \to \right){M_{s3}}\left( \leftarrow \right){M_{t2}}\left[ \begin{array}{l} \left( \to \right){M_{s4}}\\ \left( \to \right){M_{s5}}, \end{array} \right. \end{array} \right. $ |
表示Msi(i=1, 2, 3)是Mt1的学生,Msi(i=1, 2, 4)是Mt3的学生,Msi(i=3, 4, 5)是Mt2的学生.
2.2 个体成员和事件形成的物元—事元网设社会个体成员用OMi表示,物元Mi表示OMi关于特征cM1, cM2, …, cMn的量值为vM1i, vM2i, …, vMni:
| $ {M_i} = \left( {{O_{Mi}},{C_M},{V_M}} \right) = \left[ {\begin{array}{*{20}{c}} {{O_{Mi}},}&{{c_{M1}},}&{{v_{M1i}}}\\ {}&{{c_{M2}},}&{{v_{M2i}}}\\ {}& \vdots&\vdots \\ {}&{{c_{Mn}},}&{{v_{Mni}}} \end{array}} \right]. $ |
所参与的事件用事元Aj表示为
| $ {A_j} = \left( {{O_{Aj}},{C_A},{V_A}} \right) = \left[ {\begin{array}{*{20}{c}} {{O_{Aj}},}&{{c_{A1}},}&{{v_{A1j}}}\\ {}&{{c_{A2}},}&{{v_{A2j}}}\\ {}& \vdots&\vdots \\ {}&{{c_{Am}},}&{{v_{Amj}}} \end{array}} \right]. $ |
则可用物元—事元网表示Mi参与Aj所形成的社会网络.图 2为由6个成员对应的物元参与5个事件(用事元表示)所形成的物元-事元网.

|
图 2 物元—事元网 Figure 2 Matter-elements and affair-elements network |
物元Mi与事元Aj之间的关系(图 2中的连接线)可用关系元
| $ {M_1}\left[ \begin{array}{l} \left( {{{\vec R}_{{M_1}{A_1}}}} \right){A_1}\\ \left( {{{\vec R}_{{M_1}{A_2}}}} \right){A_2}\\ \left( {{{\vec R}_{{M_1}{A_5}}}} \right){A_5}, \end{array} \right.{M_2}\left[ \begin{array}{l} \left( {{{\vec R}_{{M_2}{A_1}}}} \right){A_1}\\ \left( {{{\vec R}_{{M_2}{A_2}}}} \right){A_2}\\ \left( {{{\vec R}_{{M_2}{A_3}}}} \right){A_3}\\ \left( {{{\vec R}_{{M_2}{A_4}}}} \right){A_4}, \end{array} \right. $ |
| $ {M_3}\left[ \begin{array}{l} \left( {{{\vec R}_{{M_3}{A_1}}}} \right){A_1}\\ \left( {{{\vec R}_{{M_3}{A_3}}}} \right){A_3}\\ \left( {{{\vec R}_{{M_3}{A_5}}}} \right){A_5}, \end{array} \right.{M_4}\left[ \begin{array}{l} \left( {{{\vec R}_{{M_4}{A_2}}}} \right){A_2}\\ \left( {{{\vec R}_{{M_4}{A_5}}}} \right){A_5}, \end{array} \right. $ |
| $ {M_5}\left[ \begin{array}{l} \left( {{{\vec R}_{{M_5}{A_1}}}} \right){A_1}\\ \left( {{{\vec R}_{{M_5}{A_3}}}} \right){A_3}\\ \left( {{{\vec R}_{{M_5}{A_4}}}} \right){A_4}, \end{array} \right.{M_6}\left[ \begin{array}{l} \left( {{{\vec R}_{{M_6}{A_3}}}} \right){A_3}\\ \left( {{{\vec R}_{{M_6}{A_5}}}} \right){A_5}. \end{array} \right. $ |
若只研究个体成员参与事件的某一种关系,则关系元可省略,表示为如下形式:
| $ {M_1}\left[ \begin{array}{l} \left( \to \right){A_1}\\ \left( \to \right){A_2}\\ \left( \to \right){A_5}, \end{array} \right.{M_2}\left[ \begin{array}{l} \left( \to \right){A_1}\\ \left( \to \right){A_2}\\ \left( \to \right){A_3}\\ \left( \to \right){A_4}, \end{array} \right. $ |
| $ {M_3}\left[ \begin{array}{l} \left( \to \right){A_1}\\ \left( \to \right){A_3}\\ \left( \to \right){A_5}, \end{array} \right.{M_4}\left[ \begin{array}{l} \left( \to \right){A_2}\\ \left( \to \right){A_5}, \end{array} \right. $ |
| $ {M_5}\left[ \begin{array}{l} \left( \to \right){A_1}\\ \left( \to \right){A_3}\\ \left( \to \right){A_4}, \end{array} \right.{M_6}\left[ \begin{array}{l} \left( \to \right){A_3}\\ \left( \to \right){A_5}. \end{array} \right. $ |
例如,设Mi(i=1, 2, …, 6)表示6个学生,Aj(j=1, 2, …, 5)是5个事件,则上述物元—事元网表示了6个学生参与5个事件的情况.
3 利用拓展分析研究社会网络由于社会网络是由个体成员构成的,因此可以利用对个体成员的拓展分析研究社会网络的构成.以物元网表示的社会网络为例,如利用物元的相关分析构成物元相关网,利用物元的发散分析构成物元发散网,利用物元的蕴含分析构成物元的蕴含网,利用物元的可扩分析构成物元可扩网.
例如,具有“同学关系”的个体成员,都具有同一个特征元(毕业学校,S),根据“一征多物”的发散分析,由物元M1=(O1,毕业学校,S)可以得到一个表达“同学关系”的物元网:
| $ \begin{array}{l} {M_1} = \left( {{O_1},毕业学校,S} \right) - \left| {{M_i} = \left( {{O_i},毕业学校,S} \right),} \right.\\ i = 2,3, \cdots ,n. \end{array} $ |
再如,考察某大学的教师之间的“科研合作关系”时,可以根据相关分析,分析科研成果的相关性,如从“研究领域”、“申报项目情况”、“发表论文论著情况”、“获奖情况”等方面构成物元相关网.考察科研人员的“学术地位”时,可以根据“论文论著被引用情况”、“获奖等级”、“H指数”等构成物元蕴含网.
另外,由于物元的可拓展性,导致物元网具有可拓展性,从而社会网络也具有可拓展性.因此还可以对社会网络进行拓展分析,以获得更多的信息.
4 可拓变换对社会网络的作用任何一个社会网络都会随时间的变化而变化,因而,社会网络是一个动态网络.现有的研究大都只关注静态社会网络,没有考虑社会网络随时间变化后的情况.利用动态基元网表示社会网络后,就便于对动态社会网络进行分析和研究.
此外,变换对社会网络的影响也不容小视,也必须研究实施变换后社会网络会如何变化.不同的变换,会导致社会网络发生不同的传导变换,其连接方式、网络密度、网络集中度、甚至相互性和传递性都会发生改变.因此,必须研究变换对社会网络的作用规律,才能更好地研究社会结构.
可拓变换理论与方法为研究变换对社会网络的作用提供了工具.可拓变换包括基本变换、变换的运算、传导变换、共轭变换、复合变换等等,此不详述,可参阅文献[11].
例如,对图 1所示的物元网,如果表达的是8个人的“朋友关系”,当对其中的一人实施某变换T1时,如M1升职,可表示为
| $ {T_1}{M_1} = {{M'}_1}, $ |
则该物元网中的朋友关系会发生传导变换,有些人会与M1的关系更紧密,有些人会与其疏远,有些人会与其断开关系,当然,M1也会增加新的朋友关系.图 1可能会变为如图 3所示的形式.

|
图 3 变换后的物元网 Figure 3 Matter-elements network after transformations |
对图 2所示的物元—事元网,如果表达的是6个学生参与5个公益活动的情况,当对这6个人实施某一变换时,如T=“亚运会停课一个月”,则该物元—事元网会发生变化,通过网络的变化,可以发现哪些类型的学生对“停课”敏感,哪些公益活动会受到变换的影响.
5 对社会网络的评价目前对社会网络的定量研究,大都以图论或社会计量学为工具,通过研究网络的密度来描述图中各点之间关联的紧密程度,利用中心度来研究个人或者组织在其社会网络中的地位,利用“子图”等对群体结构进行测量,以便发现网络的各个“派系”以及网络可以分成多少个凝聚子群.
在可拓学中,可以用关联度表示研究对象具有某种性质的程度,包括初等关联函数、简单关联函数、离散关联函数等形式.
例如,在可拓学中建立了实数域
| $ k\left( x \right) = \left\{ \begin{array}{l} \frac{{\rho \left( {x,X} \right)}}{{D\left( {x,{X_0},X} \right)}},\;\;\;\;\;D\left( {x,{X_0},X} \right) \ne 0,x \in X\\ - \rho \left( {x,X} \right) + 1,\;\;\;\;\;\;D\left( {x,{X_0},X} \right) = 0,x \in {X_0}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;D\left( {x,{X_0},X} \right) = 0,x \notin {X_0},x \in X\\ \frac{{\rho \left( {x,X} \right)}}{{D\left( {x,X,\hat X} \right)}},\;\;\;\;\;\;\left. {D\left( {x,X,\hat X} \right)} \right) \ne 0,x \in \Re - X\\ - \rho \left( {x,\hat X} \right) - 1,\;\;\;\;\;\left. {D\left( {x,X,\hat X} \right)} \right) = 0,x \in \Re - X \end{array} \right. $ |
可作为衡量一个对象符合某种要求的程度的函数.如果某科研机构要评价科研人员的“学术水平”,即评价特征是“学术水平”,则标准正域可作为满意区间,X-X0可作为可接受区间,
针对不同的评价特征,可以选择不同的关联函数.对于多评价特征的情况,还可建立综合关联度,用于综合评价研究对象的优劣.将其应用于社会网络研究,可以作为社会网络中的成员“聚类”或“分类”的衡量指标之一,与“密度”、“中心度”等指标相结合,可以对社会网络进行综合评价.限于篇幅,评价方法将另文详述.
6 结论与展望本文利用可拓学的理论和方法,研究了社会网络的基元表示方法,利用拓展分析研究社会网络的构成,并探讨可拓变换对社会网络的影响以及对社会网络的评价等.基于可拓学对于社会网络结构的更深入的研究,将弥补图论方法和社会计量学方法的某些不足,充分考虑社会网络中的个体成员的不同属性对网络的影响,为研究动态社会网络提供定性与定量相结合的方法.
该方法可以应用于对各领域社会网络结构的研究,如果再进一步应用可拓策略生成方法[11-12],将可应用于解决社会网络中的矛盾问题,并对上述社会网络模型进行动态管理,便于利用计算机帮助人们研究和管理社会网络.
| [1] |
Wasserman S, Faust K. Social Network Analysis: Methods and Applications[M]. New York: Cambridge University Press, 1994.
|
| [2] |
袁方, 王汉生.
社会研究方法教程[M]. 北京: 北京大学出版社, 2004.
|
| [3] |
汤汇道. 社会网络分析法述评[J].
学术界, 2009(136): 205-208.
Tang H D. Social network analysis review[J]. Academics in China, 2009(136): 205-208. |
| [4] |
斯科特. 社会网络分析法[M]. 刘军, 译. 重庆: 重庆大学出版社, 2007.
|
| [5] |
马汀·奇达夫, 蔡文彬. 社会网络与组织[M]. 王凤彬, 朱超威, 译. 北京: 中国人民大学出版社, 2007.
|
| [6] |
刘军.
社会网络分析导论[M]. 北京: 社会科学文献出版社, 2004.
|
| [7] |
伯特. 结构洞: 竞争的社会结构[M]. 任敏, 等, 译. 上海: 格致出版社, 2008.
|
| [8] |
林聚任.
社会网络分析:理论、方法与应用[M]. 北京: 北京师范大学出版社, 2009.
|
| [9] |
魏顺平. 社会网络分析及其应用案例[J].
现代教育技术, 2010, 20(3): 29-34.
Wei S P. The semantic model of AID and its realizing methods[J]. Modern Educational Technology, 2010, 20(3): 29-34. |
| [10] |
王陆. 虚拟学习社区的社会网络分析[J].
中国电化教育, 2009(2): 5-10.
Wang L. Social network analysis for virtual learning community[J]. China Educational Technology, 2009(2): 5-10. |
| [11] |
杨春燕, 蔡文.
可拓工程[M]. 北京: 科学出版社, 2007.
|
| [12] |
李立希, 杨春燕, 李铧汶.
可拓策略生成系统[M]. 北京: 科学出版社, 2006.
|
| [13] |
蔡文, 杨春燕, 何斌.
可拓逻辑初步[M]. 北京: 科学出版社, 2003.
|
| [14] |
杨春燕, 李卫华, 李小妹. 矛盾问题智能化处理的理论与方法研究进展[J].
广东工业大学学报, 2011, 28(1): 86-93.
Yang C Y, Li W H, Li X M. Recent research progress in theories and methods for theIntelligent disposal of contradictory problems[J]. Journal of Guangdong University of Technology, 2011, 28(1): 86-93. |
| [15] |
李志明, 杨春燕. 解决矛盾问题的逆向策略生成方法[J].
广东工业大学学报, 2013, 30(4): 1-5.
Li Z M, Yang C Y. Reversed strategy generating method of solving contradictory problems[J]. Journal of Guangdong University of Technology, 2013, 30(4): 1-5. |
| [16] |
杨春燕, 张拥军.
可拓策划[M]. 北京: 科学出版社, 2002.
|
| [17] |
蔡文, 杨春燕.
可拓营销[M]. 北京: 科学技术文献出版社, 2000.
|
| [18] |
蔡文, 杨春燕, 陈文伟, 等.
可拓集与可拓数据挖掘[M]. 北京: 科学出版社, 2008.
|
| [19] |
赵燕伟, 苏楠.
可拓设计[M]. 北京: 科学出版社, 2010.
|
| [20] |
杨春燕, 李小妹, 陈文伟, 等.
可拓数据挖掘方法及其计算机实现[M]. 广州: 广东高等教育出版社, 2010.
|
| [21] |
Yang C Y, Cai W. Extenics: theory, method and application[M]. Beijing:Science Press, 2013 & Columbus: The Educational Publisher, 2013.
|
 2014, Vol. 31
2014, Vol. 31