无人飞行器 (unmanned aerial vehicle,UAV),简称无人机,是指无人员在机体内部进行直接操作,仅依靠空气动力来抵消机身重量,并利用飞行控制系统自主飞行或遥控飞行来实现空中目标任务的飞行器。近年来,随着微机电系统、小型传感器技术、计算机技术和通信技术等的迅猛发展,无人机的研究成为当下一大热点。无人机可分为固定翼、旋翼和扑翼等类型,而其中四旋翼无人机以其结构简单,操作方便,可以垂直起降、空中悬停和快速航姿变换等优点,被广泛应用于军事和民用领域[1-2]。飞行姿态信息的精确测量非常重要,姿态信息的测量精度直接影响无人机的控制精度和飞行效果,是四旋翼无人机稳定飞行的基础。但是四旋翼无人机易受到磁场、紊流风场等外部环境的干扰[3-4],以及传感器工艺的限制,导致无人机姿态信息测量精度低,给无人机的实时精确控制带来较大影响。对此,国内外许多学者和研究机构都开展了对无人机飞行姿态测量的研究,并取得了一定的成果。斯坦福大学[5]研发的STARMAC系列四旋翼无人机主控制器采用单片机,姿态测量采用惯性测量单元模块,实现了四旋翼无人机姿态信息的粗略测量和基本飞行。日本千叶大学[6]研发的X-3D-BL四旋翼无人机主控制器采用Connex 400型号的微处理器,姿态测量采用集成了惯性测量单元、高度测量传感器和GPS的MNAV数字传感器,实现了无人机的定点悬停、轨迹规划和移动物体追踪等多项功能。但由于MNAV集成传感器的精度不够,难以实现无人机的自主起飞和降落等功能。宿敬亚等[7]在姿态测量过程中舍弃陀螺仪传感器,采用XR 100双轴倾角传感器来获得滚转角度信号,但由于没有直接测得角速度的测量器件,需要从其他测量信息中获取角速度数据。
以上大都采用单传感器模块和单处理器来测量和获取姿态信息,在外界干扰下,测量精度难以保证,系统稳定性不够。因此,本文在传统姿态测量硬件结构的基础上,采用双陀螺仪和双加速度计提高姿态测量精度,搭载2片基于ARM内核的嵌入式微处理器STM32组成双处理器结构以提高系统安全性和稳定性,并结合基于四元数的互补滤波算法和串级PID控制算法,实现四旋翼无人机姿态的稳定控制。
1 四旋翼无人机飞行原理 1.1 四旋翼无人机结构根据飞行器定义的机头方向不同,四旋翼无人机可分为十字型和X型两种模式[8]。十字型无人机的机头方向指向某个旋翼,而X型无人机的机头方向则指向2个旋翼正中间。相较于十字型无人机,X型无人机操作更为灵活,性能更加稳定,且便于后期扩展功能 (如搭载航拍云台和相机等) 的实现,因此,本文研究搭建X型四旋翼无人机平台。
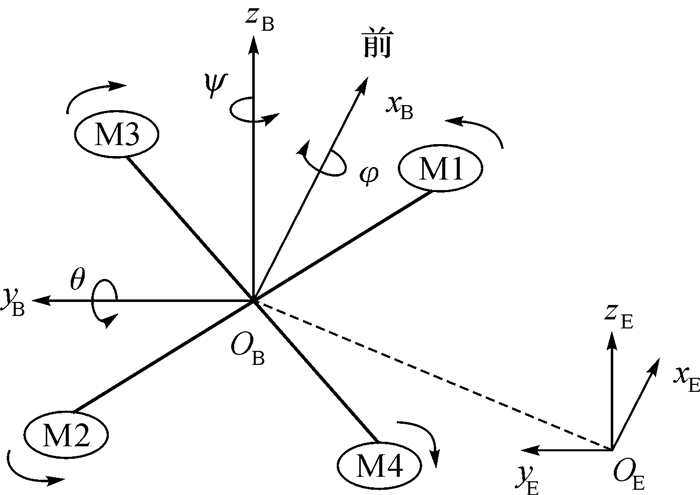
X型四旋翼无人机是一种由固联在刚性十字交叉结构上的4个独立电机驱动系统组成的飞行器[9]。安装在电机轴上的4个旋翼为飞行器提供升力,且4个旋翼的结构和半径都相同,并处于同一高度平面。4个旋翼有正反桨之分,可分为2组,处于同一对角线上的旋翼为同一组,且旋转方向一致。如图 1所示,电机M1,M2上的旋翼逆时针旋转,称为反桨;电机M3,M4上的旋翼顺时针旋转,称为正桨。
|
| 图 1 四旋翼无人机结构 Fig.1 Unmanned quadrotor mechanism |
四旋翼无人机通过改变4个电机的转速来控制4个旋翼的升力,从而控制无人机的动作变化。以图 1坐标系中OExE正方向作为机头方向,在此参考系下,四旋翼无人机可实现垂直升降、悬停、前后左右移动和偏航等基本动作。同时增大 (减小)4个电机的转速可以实现无人机的垂直升 (降) 动作,当4个旋翼提供的升力和等于整个无人机的重力且在无外界扰动时,无人机的陀螺效应和空气动力扭矩效应均被抵消,无人机达到悬停状态[10]。无人机的前后、左右移动靠其俯仰和滚转姿态下的分运动来完成,减小 (增大) 电机M1,M3转速的同时,增大 (减小) 电机M2,M4的转速,旋翼升力产生的转矩不平衡,无人机完成俯仰动作,进而实现前 (后) 移动。同理,减小 (增大) 电机M2,M3转速的同时,增大 (减小) 电机M1,M4的转速,无人机完成滚转动作,进而实现左 (右) 移动。减小 (增大) 电机M1,M2转速的同时,增大 (减小) 电机M3,M4的转速,在空气阻力下旋翼转动产生的反扭矩不平衡,无人机完成偏航动作。
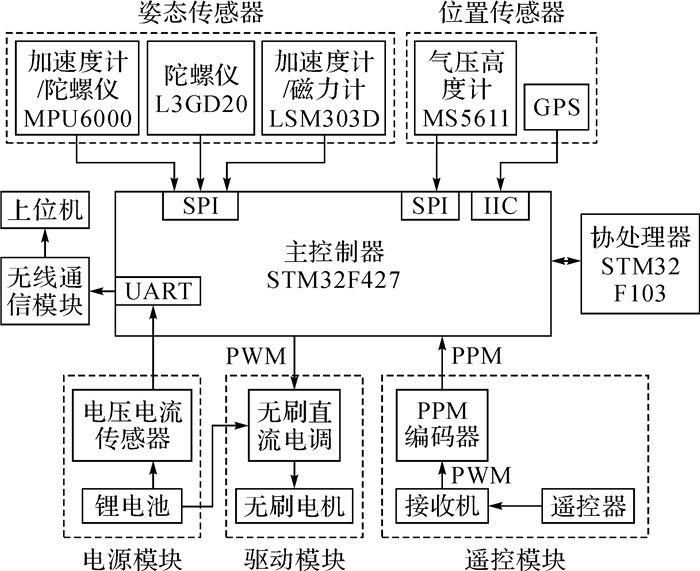
2 飞行控制系统硬件设计四旋翼无人机飞行控制系统采用模块化设计,主要由主控制器、传感器模块、驱动模块、电源模块、无线通信模块和遥控模块等组成。主控制器实时解算传感器模块采集的姿态信息和位置信息,并根据给定的飞行任务指令,结合相应的控制算法,输出适当占空比的PWM波信号来控制4个电机的转速,从而控制无人机的飞行姿态和位置。四旋翼无人机飞行控制系统的整体硬件设计结构如图 2所示。
|
| 图 2 飞行控制系统硬件设计结构框图 Fig.2 Block diagram of hardware design structure of flight control system |
图 2中无人机的硬件架构有别于传统的硬件架构,采用基于ARM内核的嵌入式主控制器和协处理器组成双处理器结构,提高整个飞行控制系统的安全性和稳定性;采用双陀螺仪和双加速度计结构,提高四旋翼无人机姿态的测量精度。
2.1 主控制器选用基于ARM Cortex M4内核的32位微处理器STM32F427作为主控制器,其工作主频高达168 MHz,满足快速解算四旋翼无人机姿态和位置信息的功能需求。STM32F427自带多个IIC,SPI和UART高速通信接口,方便与各模块进行通信,并集成多个时钟定时器,能输出多路PWM波信号便于电机控制。此外,在主控制器的基础上增加1片协处理器STM32F103来实现系统故障保护功能,当主处理器出现故障而失效时,协处理器能保证整个系统的安全和稳定。
2.2 传感器模块传感器模块包括姿态传感器和位置传感器,姿态传感器用于采集无人机姿态信息,位置传感器用于采集无人机位置信息。四旋翼无人机具有6个自由度,包括沿3个坐标轴方向的线运动和沿3个坐标轴方向的角运动[11],这些姿态信息可由传感器模块采集得到。姿态传感器包括陀螺仪、加速度计和磁力计。陀螺仪通过测量无人机的角速率,积分得到飞行姿态角来描述无人机的角运动。加速度计通过测量无人机轴向受力得到无人机3个轴向的加速度,积分得到飞行速度与距离来描述无人机的线运动。磁力计通过测量磁场强度和方向,定位无人机的飞行方向。基于误差修正和误差补偿需要,常将这3种传感器配合使用,为无人机提供准确的姿态信息[12]。位置传感器包括气压高度计和GPS,气压高度计用来测量无人机的飞行高度,GPS用来定位无人机的水平位置,两者结合使用可实现无人机室外飞行的定高需求[13]。
系统选用双陀螺仪和双加速度计的硬件结构,选用的传感器型号为六轴加速度计/陀螺仪MPU6000、三轴陀螺仪L3GD20和三轴加速度计/磁力计LSM303D。MPU6000整合了三轴陀螺仪和三轴加速度计,其中:陀螺仪对角速度的感测范围为±250、±500、±1 000与±2 000 °/s,可精确追踪飞行器的快速和慢速动作;加速度计对加速度的感测范围为±2g、±4g、±8g与±16g,可精确感知飞行器各方向加速度。为降低噪声,减少测量误差累积,增加三轴陀螺仪L3GD20与MPU6000组成双陀螺仪结构,主控制器在获取这2种陀螺仪数据信息后取两者数据的平均值进行解算。MPU6000的采样频率为1 kHz,飞行器在飞行过程中会受到振动,当其振动频率接近1 kHz时会发生共振,导致加速度计测量紊乱。为保证加速度测量精确,增加加速度传感器LSM303D与MPU6000组成双加速度计结构,LSM303D的采样频率为800 Hz,当共振发生时,可自动切换加速度计,从而避免了测量紊乱。此外,LSM303D还集成了三维数字磁力计,配合使用陀螺仪和加速度计可为飞行器提供准确姿态信息。在软硬件设计中,上述3种传感器均通过SPI接口与主控制器进行通信。
选用气压高度计MS5611来测量无人机的飞行高度,MS5611通过SPI接口与主控制器通信,其分辨率可达10 cm,满足无人机室外定高要求。选用NEO-7M GPS模块定位无人机的水平位置,NEO-7M GPS通过IIC接口与主控制器通信,其最大更新频率为10 Hz,定位精度为2.5 m,满足无人机室外飞行水平位置检测要求。
2.3 驱动模块四旋翼无人机对电机响应速度和转动速度要求较高,一般选用无刷直流电机。无刷直流电机无法单独使用,需经无刷直流电调驱动,无刷直流电调通过控制PWM波占空比来调节电机转速。选用朗宇X2216,880 kV无刷直流电机,其响应速度快、调速范围大及可靠性高。选用好盈天行者30 A无刷直流电调,其持续输出电流为30 A,最大瞬时输出电流为40 A,可对选用的电机进行快速调速。针对以上电机和电调的选型,选用直径为11英寸,螺距为47 mm的正反桨为四旋翼无人机提供升力。
2.4 电源模块选用5 300 mA、30 C,输出电压为11.1 V的锂电池作为整个飞行器的供电系统,其电池容量大,放电能力高,满足电调对大输出电流的要求,可为无人机提供更长的续航时间。锂电池输出电压太大,不能直接接入主控制器,需经电压电流传感器降压后为主控制器供电使之正常工作。
2.5 无线通信模块为了实现上位机实时显示无人机飞行数据,监测无人机的飞行状态,更好地操控无人机飞行,选用3DR无线数传模块,其发射和接收频率为433 MHz,功率为500 MW,地面通信有效距离约为1 000 m,并通过UART接口与主控制器进行通信。
2.6 遥控模块选用天地飞九通道遥控设备WFT09Ⅱ发送和接收动作指令,同时为了简化设备间的接线,增加PPM编码器,将多路PWM信号转化为1路PPM信号输入主控制器。遥控器通过2.4 G无线技术发射PPM动作指令信号,接收机接收信号后将其转化为多路PWM信号输出,并经由PPM编码器转化为1路PPM信号后输入主控制器,主控制器再将此PPM信号转化为多路PWM信号控制无刷直流电调,从而实现所需电机的速度。
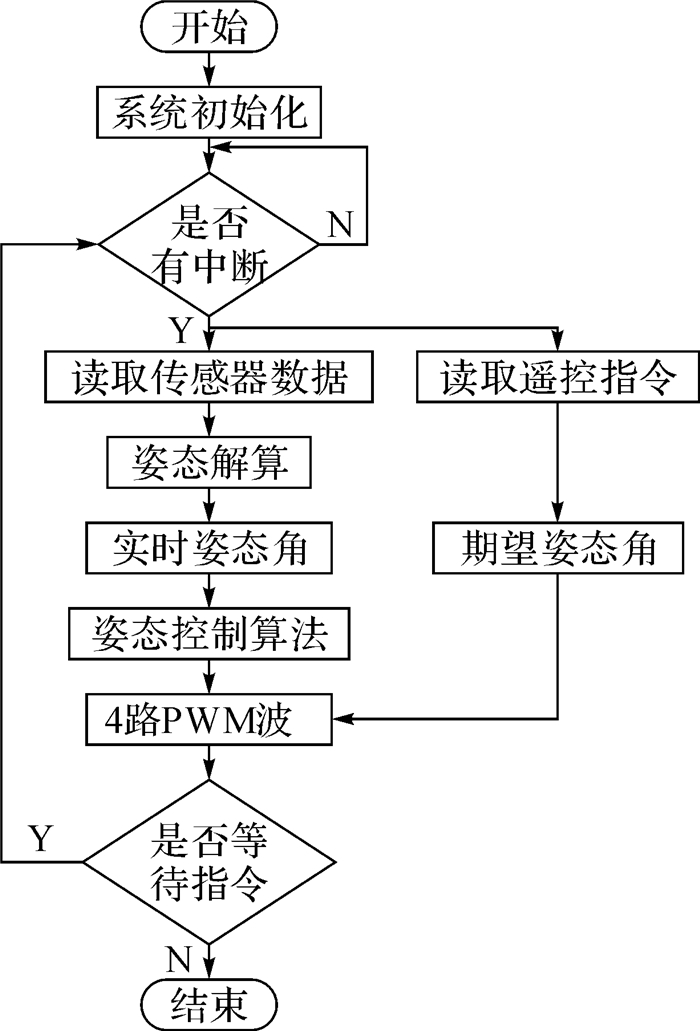
3 飞行控制系统软件设计系统软件设计的目的是在硬件设计的基础上启动四旋翼无人机飞行控制系统的各功能模块并使之正常工作,并根据飞行任务指令实现无人机的稳定飞行控制。系统上电后完成各功能模块的初始化,当有中断任务请求时,主控制器读取传感器姿态数据,然后经姿态解算得到无人机实时姿态角,并同时将主控制器通过读取遥控指令解算得到的期望姿态角输入姿态控制算法,输出4路PWM波信号控制电机转速,从而实现对四旋翼无人机的飞行控制。系统软件设计的整体结构如图 3所示。
|
| 图 3 飞行控制系统软件设计结构框图 Fig.3 Block diagram of software design structure of flight control system |
姿态解算的目的是将陀螺仪、加速度计和磁力计测量的姿态信息解算成无人机的实时姿态角,并作为系统的反馈量。陀螺仪直接测量无人机的角速率,对时间积分后得到飞行姿态角,短时间内其测量精度高,但由于噪声等影响,积分误差不断累积,长时间测量会导致其低频干扰和漂移[14]。加速度计对高频信号十分敏感,无人机在飞行过程中由于振动带来较大的高频干扰,采集到的瞬时倾角误差较大,不适合短时间内测量。磁力计通过测量磁场强度和方向,输出当前机体与地磁场的夹角,其低频特性较好,但易受周围环境磁场干扰[15],不适合短时间内测量。加速度计和磁力计短时间测量误差较大,但其测量误差均为静态误差,不随时间的累加而变化,适合长时间姿态角采集。姿态解算的实质就是结合陀螺仪、加速度计和磁力计各自的优缺点,将三者测得的姿态数据进行融合、修正后得到理想的机身姿态角。
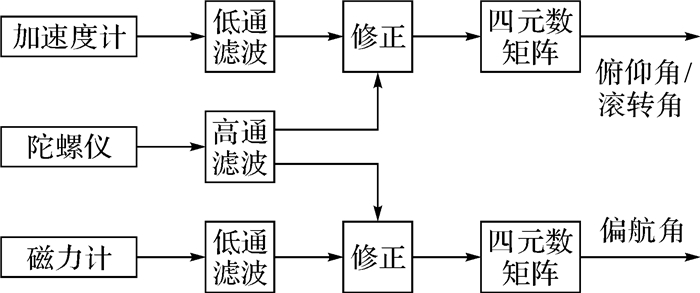
采用基于四元数的互补滤波算法[16]对无人机的姿态进行解算,其核心思想是:利用互补滤波器对陀螺仪进行高通滤波,对加速度计和磁力计进行低通滤波,然后将加速度计和磁力计滤波后的姿态角对陀螺仪滤波后的姿态角进行修正,得到修正后姿态角对应的四元数矩阵,并将其转换成具有实际物理意义的实时欧拉角。四元数互补滤波过程如图 4所示。
|
| 图 4 四元数互补滤波过程 Fig.4 Process of quaternion complementary filter |
在将姿态角四元数矩阵转换为实时欧拉角之前,先定义地理坐标系OE-xEyEzE和机体坐标系OB-xByBzB来描述无人机的相对运动。地理坐标系为地面某个参考点的静止坐标系,机体坐标系为固定在机体几何中心的动态坐标系,初始时这2个坐标系重合,如图 1所示。
四元数表示方式如下:
| $ \mathit{\boldsymbol{Q}} = {q_0} + {q_1}\mathit{\boldsymbol{i}} + {q_2}\mathit{\boldsymbol{j}} + {q_3}\mathit{\boldsymbol{k}} = {\rm{cos}}\frac{\alpha }{2} + \mathit{\boldsymbol{\mu }}{\rm{sin}}\frac{\alpha }{2} $ | (1) |
式中:μ为旋转轴单位矢量;α为旋转角度,即将机体坐标系OB-xByBzB绕μ转动1个角度就能与地理坐标系OE-xEyEzE重合。
机体坐标系OB-xByBzB到地理坐标系OE-xEyEzE的变换矩阵用四元数表示为[17]:
| $ \boldsymbol{C}_{\rm{B}}^{\rm{E}} = \left( {\begin{array}{*{20}{c}} {{q^2}_0 + {q^2}_1-{q^2}_2-{q^2}_3}&{2({q_1}{q_2}-{q_0}{q_3})}&{2({q_1}{q_3} + {q_0}{q_2})}\\ {2({q_1}{q_2} + {q_0}{q_3})}&{{q^2}_0 - {q^2}_1 + {q^2}_2 - {q^2}_3}&{2({q_2}{q_3} - {q_0}{q_1})}\\ {2({q_1}{q_3} - {q_0}{q_2})}&{2({q_2}{q_3} + {q_0}{q_1})}&{{q^2}_0 - {q^2}_1 - {q^2}_2 + {q^2}_3} \end{array}} \right) $ | (2) |
采用欧拉角描述无人机的姿态时,机体坐标系OB-xByBzB到地理坐标系OE-xEyEzE的变换矩阵RBE为[18]:
| $ \boldsymbol{R}_{\rm{B}}^{\rm{E}} = \left( {\begin{array}{*{20}{c}} {\rm{c}\theta \rm{c}\psi }&{-\rm{c}\varphi \rm{s}\psi + \rm{s}\theta \rm{s}\varphi \rm{c}\psi }&{\rm{s}\varphi \rm{s}\psi + \rm{s}\theta \rm{c}\varphi \rm{c}\psi }\\ {\rm{c}\theta \rm{s}\psi }&{\rm{c}\varphi \rm{c}\psi + \rm{s}\theta \rm{s}\varphi \rm{s}\psi }&{-\rm{s}\varphi \rm{c}\psi + \rm{s}\theta \rm{c}\varphi \rm{s}\psi }\\ {-\rm{s}\theta }&{\rm{c}\theta \rm{s}\varphi }&{\rm{c}\theta \rm{c}\varphi } \end{array}} \right) $ | (3) |
式中:s和c分别表示正弦和余弦符号;θ,φ和ψ表示机体欧拉角,θ为俯仰角,φ为滚转角,ψ为偏航角。
四元数和欧拉角是无人机姿态角的2种表达方式,因此机体坐标系OB-xByBzB到地理坐标系OE-xEyEzE的变换矩阵是一致的,即有:
| $ \boldsymbol{C}_{\rm{B}}^{\rm{E}} = \boldsymbol{R}_{\rm{B}}^{\rm{E}} $ | (4) |
由式 (4) 解得四元数矩阵转换为欧拉角方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {\varphi = {\rm{arctan}}[\frac{{2({q_2}{q_3} + {q_0}{q_1})}}{{q_0^2 - q_1^2 - q_2^2 + q_3^2}}]}\\ {\theta = {\rm{arcsin}}[ - 2({q_1}{q_3} - {q_0}{q_2})]}\\ {\psi = {\rm{arctan}}[\frac{{2({q_1}{q_2} + {q_0}{q_3})}}{{q_0^2 + q_1^2 - q_2^2 - q_3^2}}]} \end{array}} \right. $ | (5) |
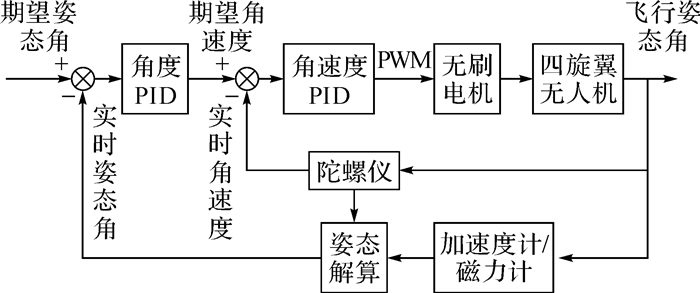
四旋翼无人机是一种欠驱动系统,具有非线性、强耦合和干扰敏感的特性[19],姿态控制是实现其稳定飞行的核心。PID算法不需要精确的物理模型[20],在工程实践中应用较为广泛,本文在传统单环PID控制的基础上,使用2个PID控制器组成串级PID控制策略,提高四旋翼无人机飞行控制系统的抗干扰性和适应性,增强系统鲁棒性。串级PID分为内外两环,外环为角度PID环,内环为角速度PID环。外环输入期望姿态角与实时姿态角的偏差,并将输出的期望角速度与实时角速度的偏差作为内环输入,最终转换为PWM波信号控制电机转速。串级PID控制原理框图如图 5所示。
|
| 图 5 串级PID控制框图 Fig.5 Block diagram of cascade PID control |
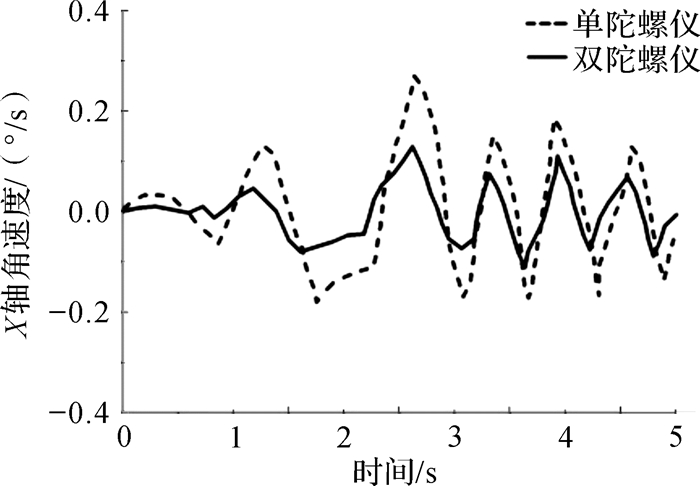
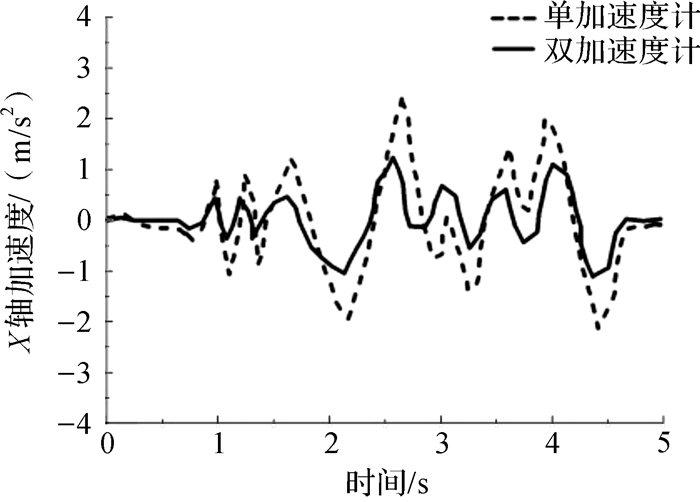
将X型四旋翼无人机上电初始化,在对无人机进行小角度扰动下通过陀螺仪和加速度计传感器测量无人机三轴加速度和三轴角速度。以无人机三轴中的X轴为测量对象,通过单、双陀螺仪测量得到的角速度对比如图 6所示,通过单、双加速度计测量得到的加速度对比如图 7所示。
|
| 图 6 X轴角速度对比 Fig.6 Comparison of angular velocity for X axis |
|
| 图 7 X轴加速度对比 Fig.7 Comparison of acceleration for X axis |
小角度扰动下,X轴角速度和加速度目标值约为0。图 6中,单陀螺仪测量的角速度最大误差约为±0.3°/s,双陀螺仪测量的角速度最大误差约为±0.1°/s。图 7中,单加速度计测量的加速度最大误差约为±3 m/s2,双加速度计测量的加速度最大误差约为±1 m/s2。对比结果表明,采用双陀螺仪和双加速度计的架构能够提高无人机角速度和加速度的测量精度。
4.2 PID调参实验姿态控制算法中双环PID参数的合理设置是四旋翼无人机能够稳定飞行的基础。以搭建的X型四旋翼无人机作为实验平台,对无人机的俯仰、滚转及偏航三种姿态分别进行PID参数调节。为保证PID参数调节过程中的机身安全,由安全绳固定X型四旋翼无人机,通过观察无人机对3种姿态的响应情况来确定PID参数的优劣。PID参数调节实验平台如图 8所示。

|
| 图 8 PID参数调节实验平台 Fig.8 Experiment platform of PID parameter adjustment |
双环PID调节顺序为:先调节外环参数,再调节内环参数。外环以P调节为主,内环角速度是核心,需将P,I和D三者结合调节。外环P调节用于将姿态偏差角度纠正回期望角度。内环P调节用于将姿态偏差角速度纠正回期望角速度,I调节用于消除角速度稳态误差,D调节用于增加系统阻尼力。通过实验平台对双环PID参数反复调节,取表 1中参数时X型四旋翼无人机姿态保持稳定。
| 调节策略 | 俯仰 | 滚转 | 偏航 |
| 外环P调节 | 3.500 | 3.200 | 3.400 |
| 内环P调节 | 0.163 | 0.173 | 0.155 |
| 内环I调节 | 0.200 | 0.150 | 0.258 |
| 内环D调节 | 0.006 | 0.007 | 0 |
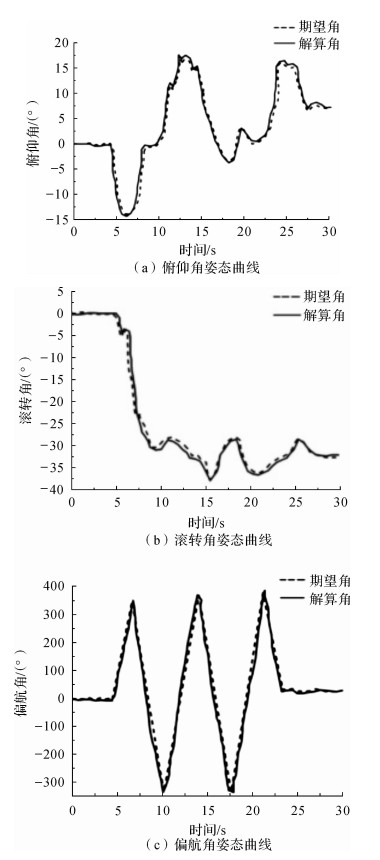
将表 1中PID参数通过上位机写入主控制器,将搭建的X型四旋翼无人机在风速不大且空旷的室外进行试飞,并将试飞数据进行分析整理,绘制出期望姿态角与实际解算姿态角对比曲线,如图 9所示。
|
| 图 9 姿态角输出曲线 Fig.9 Attitude angle output curves |
图中俯仰角最大误差约为±1.5°,滚转角最大误差约为±2°,偏航角最大误差约为±1°,表明PID参数设置较为合理,整体姿态动态误差小。
5 结论本文设计了一种基于STM32系列微处理器的X型四旋翼无人机,整个设计方案围绕系统软硬件架构展开,硬件部分搭建主控制器与各模块的运行环境,软件部分启动主控制器与各模块的正常功能,并采用四元数互补滤波算法和串级PID算法对飞行姿态进行解算和控制输出。通过实验验证获得如下结论:
1) 采用双陀螺仪和双加速度计的硬件架构在一定程度上提高了四旋翼无人机的飞行姿态测量精度;
2) 采用四元数互补滤波算法和串级PID算法有效实现了四旋翼无人机的姿态解算和姿态控制过程,飞行姿态误差波动小,满足设计要求;
3) 本设计提供了一个飞行试验平台,为后续四旋翼无人机飞行控制系统的深入研究奠定了基础。
| [1] | FLOREANO D, WOOD R J. Science, technology and the future of small autonomous drones[J]. Nature, 2015, 521: 460–466. DOI:10.1038/nature14542 |
| [2] |
鲜斌, 古训, 刘祥, 等.
小型无人直升机姿态非线性鲁棒控制设计[J]. 控制理论与应用, 2014, 31(4): 409–416.
XIAN Bin, GU Xun, LIU Xiang, et al. Nonlinear robust attitude control for a miniature unmanned helicopter[J]. Control Theory & Applications, 2014, 31(4): 409–416. |
| [3] |
何勇灵, 陈彦民, 周岷峰.
四旋翼飞行器在风场扰动下的建模与控制[J]. 中国惯性技术学报, 2013, 21(5): 624–630.
HE Yong-ling, CHEN Yan-min, ZHOU Min-feng. Modeling and control of a quadrotor helicopter under impact of wind disturbance[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 624–630. |
| [4] | KENDOUL F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems[J]. Journal of Field Robotics, 2012, 29(2): 315–378. DOI:10.1002/rob.20414 |
| [5] | HOFFMANNG, RAJNARAYAN D G, WASLANDER S L, et al. The Stanford testbed of autonomous rotorcraft for multi agent control (STARMAC)[C]//Digital Avionics Systems Conference, Salt Lake, Oct. 24-28, 2004. |
| [6] | KENDOUL F, YU Z, NONAMI K. Guidance and nonlinear control system for autonomous flight of minirotorcraft unmanned aerial vehicles[J]. Journal of Field Robotics, 2010, 27(3): 311–334. |
| [7] |
宿敬亚, 张瑞峰, 王新华, 等.
基于滤噪微分器的四旋翼飞行器控制[J]. 控制理论与应用, 2009, 26(8): 827–832.
SU Jing-ya, ZHANG Rui-feng, WANG Xin-hua, et al. Controlling a four-rotor aircraft based on noise-attenuation differentiator[J]. Control Theory & Applications, 2009, 26(8): 827–832. |
| [8] | KALANTARI A, SPENKO M. Modeling and performance assessment of the HyTAQ, a hybrid terrestrial/aerial quadrotor[J]. IEEE Transactions on Robotics, 2014, 30(5): 1278–1285. DOI:10.1109/TRO.2014.2337555 |
| [9] |
安宏雷, 李杰, 王剑, 等.
应用于四旋翼无人机角速度估计的几何滑模观测器设计[J]. 国防科技大学学报, 2013, 35(6): 165–170.
AN Hong-lei, LI Jie, WANG Jian, et al. Geometric sliding mode observer design with application to angular velocity estimation of quadrotor UAV[J]. Journal of National University of Defense Technology, 2013, 35(6): 165–170. |
| [10] |
宿敬亚, 樊鹏辉, 蔡开元.
四旋翼飞行器的非线性PID姿态控制[J]. 北京航空航天大学学报, 2011, 37(9): 1054–1058.
SU Jing-ya, FAN Peng-hui, CAI Kai-yuan. Attitude control of quadrotor aircraft via nonlinear PID[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9): 1054–1058. |
| [11] |
杨立本, 章卫国, 黄得刚.
基于ESO的欠驱动四旋翼飞行器轨迹鲁棒控制[J]. 系统工程与电子技术, 2015, 37(9): 2102–2108.
YANG Li-ben, ZHANG Wei-guo, HUANG De-gang. Robust trajectory tracking control for underatuated quadrotor UAV based on ESO[J]. Systems Engineering and Electronics, 2015, 37(9): 2102–2108. DOI:10.3969/j.issn.1001-506X.2015.09.22 |
| [12] |
刘建业, 贾文峰, 赖际舟, 等.
微小型四旋翼飞行器多信息非线性融合导航方法及实现[J]. 南京航空航天大学学报, 2013, 45(5): 575–582.
LIU Jian-ye, JIA Wen-feng, LAI Ji-zhou, et al. Multi-information nonlinear fusion technology of micro quadrotor aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(5): 575–582. |
| [13] | ZHANG X, XIAN B, ZHAO B, et al. Autonomous flight control of a nano quadrotor helicopter in a GPS-denied environment using on-board vision[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6392–6403. DOI:10.1109/TIE.2015.2420036 |
| [14] |
廖懿华, 张铁民, 廖贻泳.
基于模糊-比例积分偏差修正的多旋翼飞行器姿态测算系统[J]. 农业工程学报, 2014, 30(20): 19–27.
LIAO Yi-hua, ZHANG Tie-min, LIAO Yi-yong. Multi-rotor aircraft attitude detection system based on fuzzy-proportion integration deviation correction[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(20): 19–27. DOI:10.3969/j.issn.1002-6819.2014.20.003 |
| [15] |
李翔, 李智.
航姿参考系统三轴磁强计校正的点积不变法[J]. 仪器仪表学报, 2012, 33(8): 1813–1818.
LI Xiang, LI Zhi. Dot product invariance method for the calibration of three-axis magnetometer in attitude and heading reference system[J]. Chinese Journal of Scientific Instrument, 2012, 33(8): 1813–1818. |
| [16] | FOURATI H. Heterogeneous data fusion algorithm for pedestrian navigation via foot-mounted inertial measurement unit and complementary filter[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 221–229. DOI:10.1109/TIM.2014.2335912 |
| [17] | DEMARINA H G, PEREDA F J, GIRON-SIERRA J M, et al. UAV attitude estimation using unscented kalman filter and TRIAD[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4465–4474. DOI:10.1109/TIE.2011.2163913 |
| [18] | ISLAM S, LIU P X, EL SADDIK A. Robust control of four-rotor unmanned aerial vehicle with disturbance uncertainty[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1563–1571. DOI:10.1109/TIE.2014.2365441 |
| [19] |
杨荟憭, 姜斌, 张柯.
四旋翼直升机姿态系统的直接自修复控制[J]. 控制理论与应用, 2014, 31(8): 1053–1060.
YANG Hui-liao, JIANG Bin, ZHANG Ke. Direct self-repairing control for four-rotor helicopter attitude systems[J]. Control Theory & Applications, 2014, 31(8): 1053–1060. |
| [20] | ALAIMO A, ARTALE V, MILAZZO C L R, et al. PID controller applied to hexacopter flight[J]. Journal of Intelligent & Robotic Systems, 2014, 73(1/4): 261–270. |


