2. 重庆齿轮箱有限责任公司, 重庆 402263
2. CN GPower Gearbox Co., Ltd., Chongqing 402263, China
立磨减速机是立式磨机的核心部件,其传动系统通常由锥齿轮传动、平行轴齿轮传动、行星齿轮传动等组合而成.齿轮修形能够改善齿面的润滑状态及啮合平稳性,从而减小齿轮受载变形和制造、装配误差引起的啮合冲击,获得较为均匀的齿面荷载分布.许多学者对齿轮修形技术进行了研究,并发表了重要研究论文.Fuentes,Bergseth等探讨了齿廓和齿向修形方法[1, 2].Tesfahunegn,Sankar,Simon及Bahk等研究了修形对齿轮强度、接触状态、动力学性能等的影响[3, 4, 5, 6].孙建国等基于有限元软件LS-DYNA计算了齿轮修形对啮入冲击的影响[7].吴勇军等研究了基于接触有限元分析的斜齿轮精确齿廓修形设计,并进行了振动对比验证实验[8].林腾蛟等通过改变主动轮的修形量,计算对应的齿轮疲劳寿命,得出了合理选择修形量才能提高齿轮的疲劳寿命的结论[9].王丹等采用ANSYS的APDL参数化语言建立齿轮传动模型,求出了基于热变形的齿廓最大修形量,结合修形理论,得出了修形曲线[10].陈思雨等考虑了齿轮啮合刚度及静态传递误差,研究了不同修形量和修形长度对齿轮动态性能的影响[11].马辉等分析了不同修缘量对时变啮合刚度、静态传递误差以及系统振动响应的影响[12].
本文借助Romax软件,建立立磨减速机传动系统模型.通过分析平行级斜齿轮副及行星级直齿轮副的接触情况,选择偏载现象较为严重的齿轮副,采用遗传算法对其修形参数进行寻优,以建立优化后的模型,并对比分析修形前后齿轮副的传动误差、单位长度的法向载荷及最大接触应力.本优化方法简便快捷,且有较好的效果,可为立磨减速机的设计提供技术支撑.
本文所研究的立磨减速机由三级齿轮传动组成,分别为一级锥齿轮、一级平行轴斜齿轮和一级直齿行星传动.图 1为斜齿轮及直齿行星传动的接触应力分布.

|
| 图 1 斜齿轮及直齿行星传动的接触应力分布 Fig. 1 Contact stress distribution of helical gear and spur planetary gear transmission (PGT) |
通过对比,发现斜齿轮副的偏载更为严重,因此主要对斜齿轮副进行齿形优化分析.平行级斜齿轮副的参数如表 1所示.
借助Romax软件,建立立磨减速机传动系统的三维实体模型,并设置各部件材料、热处理、润滑状态等以最大程度模拟真实系统.建立的Romax模型如图 2所示.
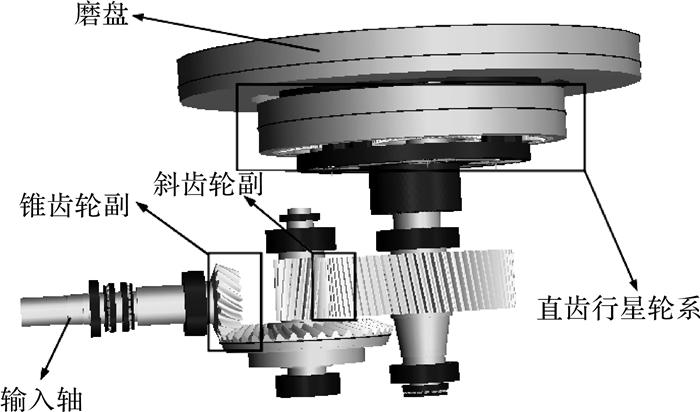
|
| 图 2 立磨减速机传动系统 Fig. 2 Transmission system of vertical mill gearbox |
| 参 数 | 主动轮 | 从动轮 | |
| 齿数z | 19 | 70 | |
| 模数m/mm | 20 | ||
| 压力角α/(°) | 20 | ||
| 螺旋角β/(°) | 9 | ||
| 变位系数x/mm | 0.341 | 0.391 9 | |
| 齿宽b/mm | 470 | 450 | |
| 中心距a/mm | 915 | ||
| 齿顶高系数h* | 1 | ||
| 顶隙系数c* | 0.25 |
模型包括各级齿轮、轴承、轴、行星架等,行星架通过导入有限元模型以考虑其柔性.动力由输入轴输入,经过锥齿轮副、平行级斜齿轮副、行星级传动,最终由行星架传递给磨盘输出.输入功率为1 500 kW,输入转速为990 r/min.
传动误差是用来描述齿轮传动平稳性的参数,它的波动会直接反映被动齿轮的转动不均匀,较大的传动误差波动对传动系统的振动、噪声有着重要而直接的影响[13, 14].因此,齿轮传动误差定义为被动齿轮实际转角滞后于理论转角之值Δθ,当其恒定时,齿轮就不会产生振动.图 3给出了平行级斜齿轮副的传动误差曲线,其中横坐标为主动轮滚动角,纵坐标为传动误差.
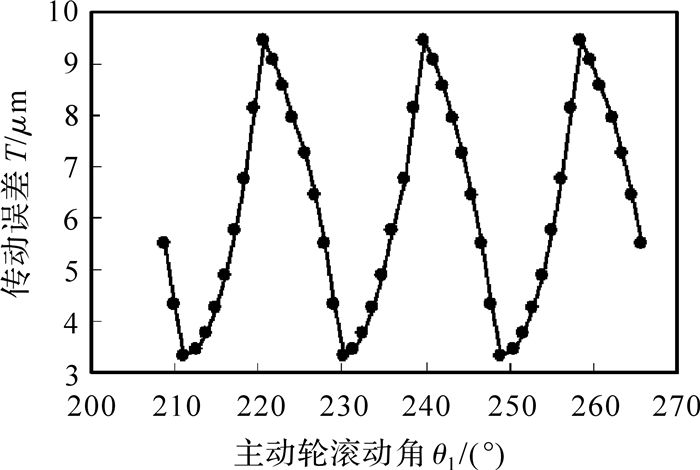
|
| 图 3 平行级斜齿轮副传动误差 Fig. 3 Transmission error of parallel helical gear pair |
由图 3可知,主动轮转动过程中,传动误差最大值为9.5 μm,最小值为3.3 μm,均值在6.5 μm左右,而波动范围达到了6.13 μm.由此可见,平行级斜齿轮副运转平稳性有待提高.
图 4给出了平行级斜齿轮副优化前主、从动轮单位长度法向载荷分布.
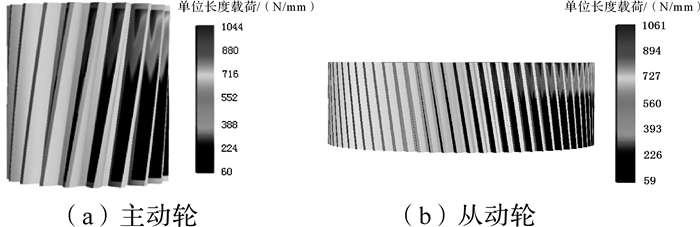
|
| 图 4 优化前主动轮和从动轮单位长度法向载荷 Fig. 4 Normal load per unit length of driving and driven gear before optimization |
由图 4可知,由于轴的变形、错位及温度等因素对轮齿啮合性能的影响,啮合齿面出现了较严重的偏载.主动轮和从动轮的最大单位长度载荷分别为1 044 N/mm和1 061 N/mm,而大部分齿面的最大单位长度载荷在200 N/mm左右,由此可见,齿面没有得到充分利用.
与单位长度法向载荷分布类似,从最大接触应力分布图也可以看出明显的偏载现象,图 5给出了主、从动轮的最大接触应力,主动轮和从动轮的最大接触应力值分别为838 MPa和847 MPa.而大部分齿面的最大接触应力值在300 MPa左右.
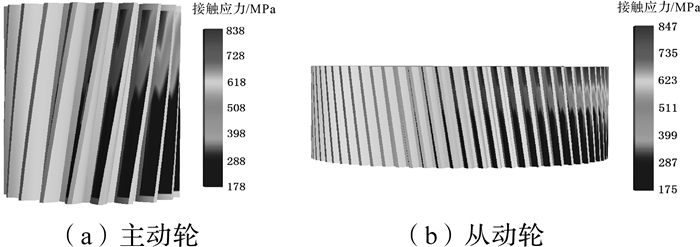
|
| 图 5 优化前主动轮和从动轮最大接触应力 Fig. 5 Maximum contact stress of driving and driven gear before optimization |
由平行级斜齿轮副主、从动轮单位长度法向载荷及最大接触应力的分布情况可以看出,齿轮存在较严重的偏载,因此有必要对轮齿进行修形,以优化齿面接触性能,改善齿轮传动的平稳性.
加工及安装误差、受载弹性变形及热变形的存在,使得啮合线上主、从动轮的基节不相等而产生啮入及啮出干涉现象.齿轮的齿廓修形就是将齿廓的齿顶或齿根处由变形误差、齿形误差等引起的干涉量修去,弥补由实际啮合引起的基节偏差,从而减小齿轮传动中的啮合冲击.图 6为齿廓修形示意图,Δmax为最大修形量,N1N2为理论啮合线,B1B2为实际啮合线.
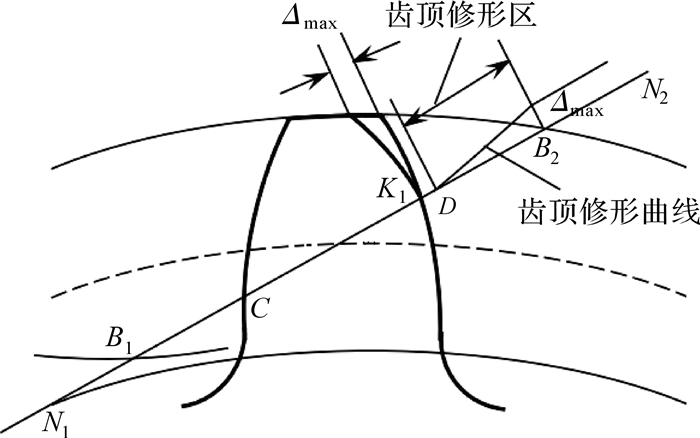
|
| 图 6 齿廓修形示意图 Fig. 6 Sketch of profile modification |
实际工作条件下,由于齿向误差,轴承安装孔的位置误差,轴、轴承以及箱体的变形等,轮齿会出现在齿宽方向上偏向一侧接触的情况,从而载荷沿齿宽分布不均.齿轮齿向修形就是沿齿长方向将由于齿轮制造误差、弹性变形及热变形而嵌入另一个轮齿的部分修去,抵消齿轮(轴)的弹性变形和螺旋角畸变,使啮合齿面不发生棱边接触,并尽量使载荷沿齿宽方向均布.图 7为齿向修形示意图,其中:Cc为鼓形量,b为齿宽,Rc为鼓形半径.
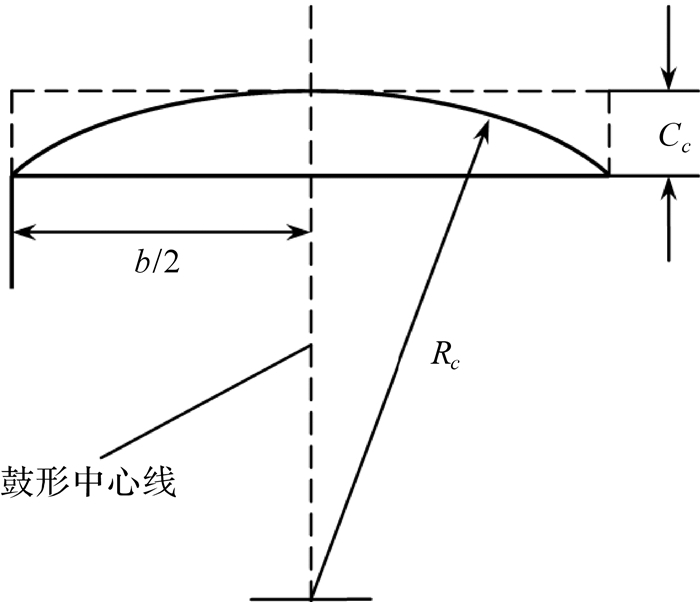
|
| 图 7 齿向修形示意图 Fig. 7 Sketch of lead modification |
遗传算法是模仿生物的遗传、进化原理,并引用了随机统计理论而形成的.在求解过程中,遗传算法从一个初始变量群体开始,一代代地寻找问题的最优解,直至满足收敛判据或预先设定的迭代次数为止.遗传算法已被证实在处理含连续、离散变量的优化问题中的有效性.它提供了求解非线性、多模型、多目标等复杂系统优化问题的通用框架,是一种实用、高效、强鲁棒性的优化技术,非常适用于轮齿齿形的优化设计[15, 16, 17, 18].标准遗传算法实施步骤包括编码、初始群体生成、适应度评估和检测、选择、交叉和变异.优化流程如图 8所示.
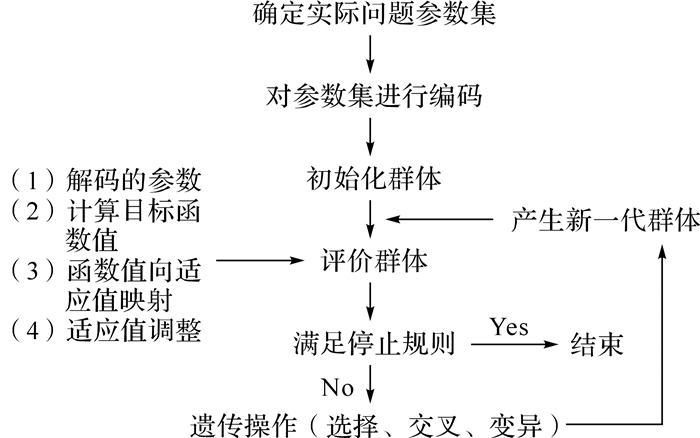
|
| 图 8 遗传算法流程图 Fig. 8 The flow chart of genetic algorithm |
本文选取立磨减速机平行级斜齿轮副为研究对象,对于设定的优化目标,即传动误差波动值最小,之前并不知道哪些修形参数对其影响较大,因此,先对选取的参数设定一个大致的取值范围,通过第1次优化的结果来调整参数取值范围,以进一步确定最优值.
本文选取主、从动齿轮齿廓的修缘量和起始角、齿向的偏斜和鼓形量为设计变量,其中齿顶采用线性修缘的方法.给定第1次优化范围:齿廓修缘量,0~30 μm;齿向鼓形量,0~30 μm;齿向偏斜,-30~30 μm;主动轮修缘起始角,29.981°~39.471°;从动轮修缘起始角,24.564°~27.14°,修缘起始角取值范围为单齿啮合最高点至有效齿廓最高点.
以从动轮齿向偏斜为例,给出修形参数的优化过程,如图 9所示.第1次优化后,从动轮的齿向偏斜趋近于-30 μm,而给定的齿向偏斜取值范围为-30~30 μm.第1次优化的结果较接近给定取值范围的边界值,因此有必要重新选定取值范围,进行第2次优化.选取第2次优化范围:-50~-10 μm,第2次优化后,齿向偏斜趋近于-37.5 μm,即为最终优化结果.
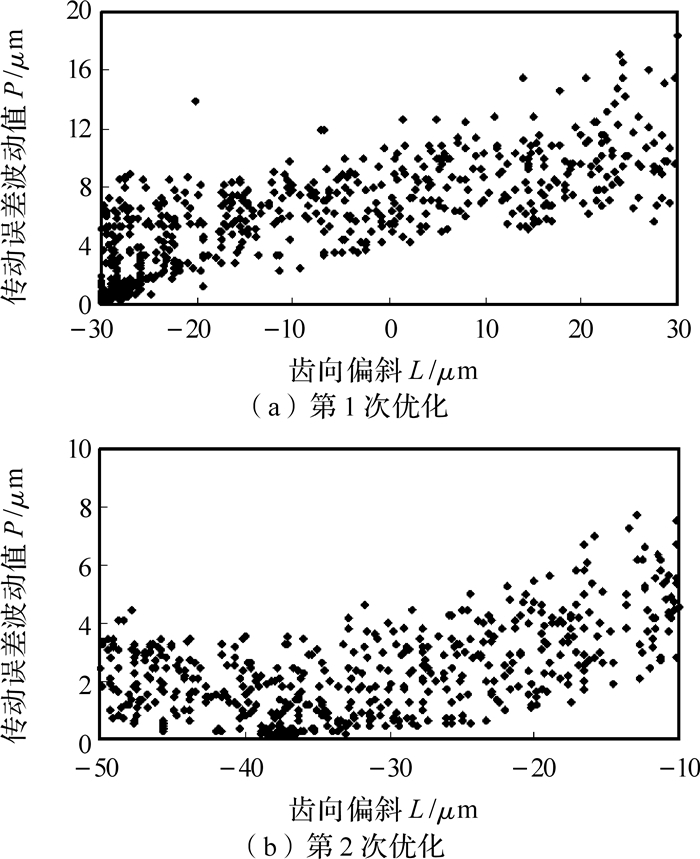
|
| 图 9 从动轮齿向偏斜优化过程 Fig. 9 Lead slope optimization procedure of driven gear |
表 2给出了第1次及第2次优化后各变量的最优值.
| 齿轮 | 优化次数 | 齿廓 | 齿向 | ||
| 修缘 /μm |
起始角 /(°) |
鼓形 /μm |
偏斜 /μm |
||
| 主动轮 | 第1次 | 8.13 | 30.725 | 6.16 | -22.48 |
| 第2次 | 13.24 | 32.277 | 9.67 | -16.34 | |
| 从动轮 | 第1次 | 13.03 | 25.154 | 7.46 | -29.93 |
| 第2次 | 11.65 | 24.951 | 3.99 | -37.52 | |
根据优化得到的修形参数最优值,可以确定齿轮在齿宽及齿廓方向的修形曲线.图 10、图 11分别为主、从动轮的修形曲线,负值代表去除材料.
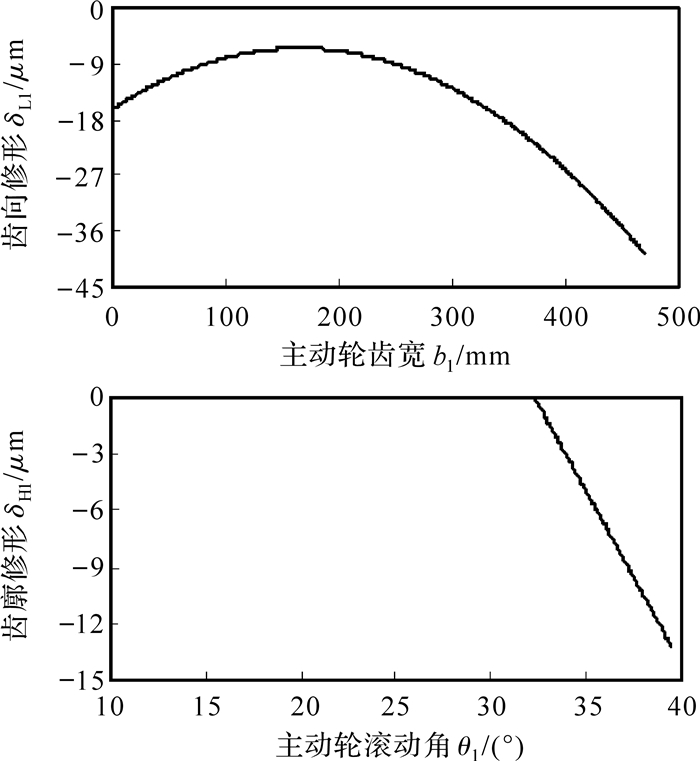
|
| 图 10 主动轮修形曲线 Fig. 10 Modification curve of driving gear |
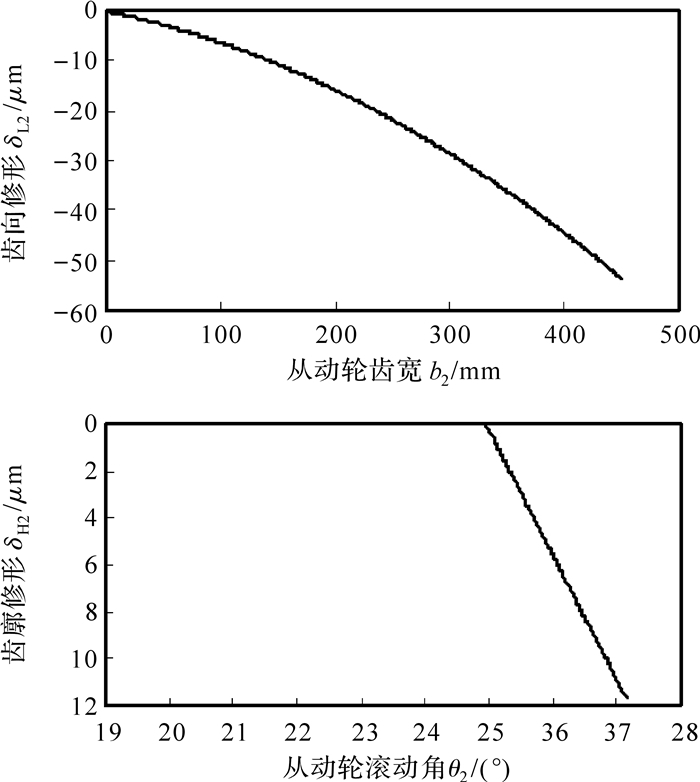
|
| 图 11 从动轮修形曲线 Fig. 11 Modification curve of driven gear |
将优化所得的修形量应用于平行级斜齿轮副,对修形后的齿轮副模型进行传动误差、齿面接触等方面的分析.
图 12给出了优化后斜齿轮副的传动误差曲线.由图可知,传动误差的均值较优化前有所增加,主要原因是修形之后,主、从动齿轮均去除了部分材料.但主要影响齿轮振动及噪声大小的是传动误差的波动值,所以一般更注重波动值的变化.优化后消除了传动误差的部分突变点,且传动误差波动值从优化前的6.13 μm减小到了0.59 μm,意味着优化后传动误差波动大幅减小,轮齿运行会更加平稳,振动更小.
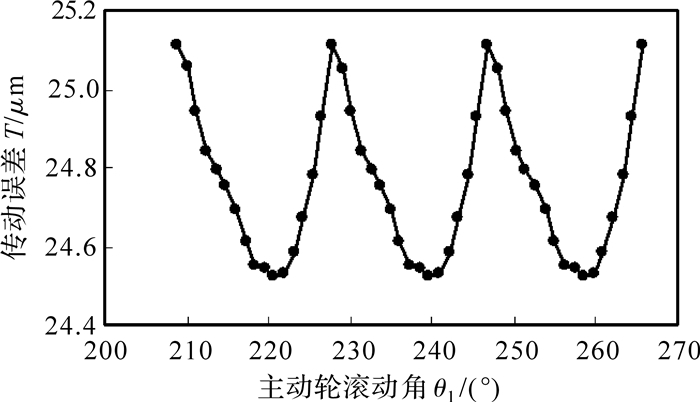
|
| 图 12 优化后斜齿轮副传动误差 Fig. 12 Transmission error of helical gear pair after optimization |
图 13为优化前后立磨减速机斜齿轮副传动误差前8阶次的谐波幅值,工程上一般关心前3阶.由图可知,优化后,前3阶谐波幅值均有不同程度的减小,特别是第1阶,幅值由2.81 μm降到了0.25 μm左右,优化效果较为明显.
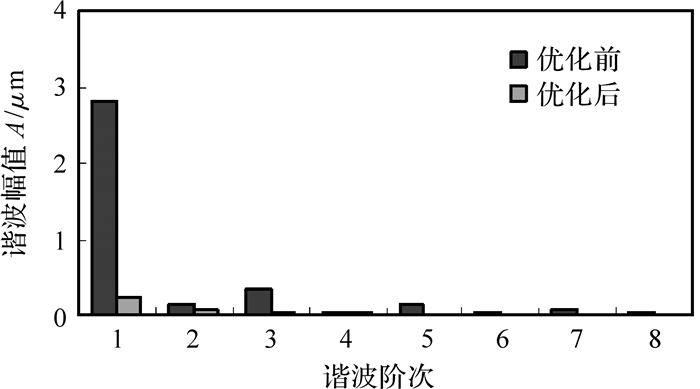
|
| 图 13 优化前后传递误差谐波 Fig. 13 Harmonic of transmission error before and after optimization |
图 14为优化前后轮齿转动过程中单齿所受载荷的变化曲线.在单个轮齿的啮入到啮出过程中,其所受的载荷先增大后减小.优化后,轮齿载荷的最大值稍有减小,曲线变化比较平稳,消除了突变尖点,减少了冲击.
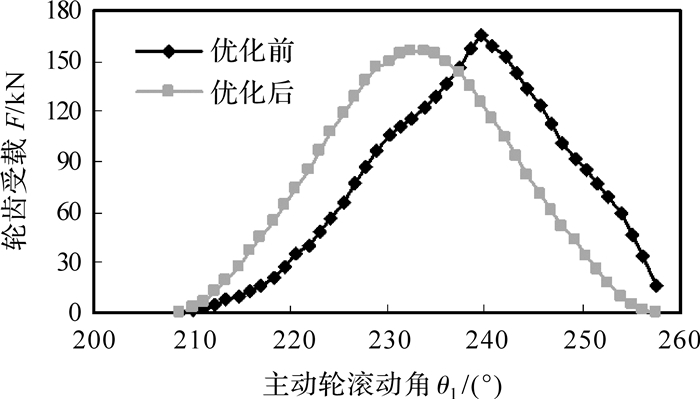
|
| 图 14 优化前后单齿所受载荷 Fig. 14 Load of a single tooth before and after optimization |
图 15给出了优化后单位长度法向载荷,主、从动轮单位长度载荷分别由1 044,1 061 N/mm减小到了480 N/mm.优化后,最大载荷分布在齿面中部,且比较均匀,可有效解决偏载问题.

|
| 图 15 优化后主动轮和从动轮单位长度法向载荷 Fig. 15 Normal load per unit length of driving and driven gear after optimization |
图 16为优化后主、从动轮的最大接触应力分布图.主、从动轮的最大接触应力分别由838,847 MPa降低至558 MPa,且分布较为均匀.

|
| 图 16 优化后主动轮和从动轮最大接触应力 Fig. 16 Maximum contact stress of driving and driven gear before optimization |
1)利用Romax软件建立了立磨减速机的传动系统模型,采用遗传算法对平行级斜齿轮副主动轮和从动轮的齿向、齿廓的修形量进行优化,得出主、从动轮的最佳修形量.
2)将优化所得的最佳修形量应用于斜齿轮传动,大幅度减小了传动误差的波动值.通过齿形优化,轮齿所受的载荷变化更加平滑,减少了冲击,提高了传动系统的平稳性.
3)优化后轮齿的单位长度法向载荷及最大接触应力分布都比较均匀,改善了轮齿的偏载问题;数值上也有大幅度的减小,优化了轮齿啮合性能.
| [1] | FUENTES A,NAGAMOTO H,LITVIN F L,et al.Computerized design of modified helical gears finished by plunge shaving[J].Computer Methods in Applied Mechanics and Engineering,2010,199(25/28):1677-1690. |
| Click to display the text | |
| [2] | BERGSETH E,BJORKLUND S.Logarithmical crowning for spur gears[J].Journal of Mechanical Engineering,2010,56(4):239-244. |
| Click to display the text | |
| [3] | TESFAHUNEGN Y A,ROSA F,GORLA C.The effects of the shape of tooth profile modifications on the transmission error,bending,and contact stress of spur gears[J].Proceedings of the Institution of Mechanical Engineers:part C:Journal of Mechanical Engineering Science,2010,224(8):1749-1758. |
| Click to display the text | |
| [4] | SANKAR S,NATARAJ M.Profile modification:a design approach for increasing the tooth strength in spur gear[J].International Journal of Advanced Manufacturing Technology,2011,55(1/4):1-10. |
| Click to display the text | |
| [5] | SIMON V V.Influence of tooth modifications on tooth contact in face-hobbed spiral bevel gears[J].Mechanism and Machine Theory,2011,46(12):1980-1998. |
| Click to display the text | |
| [6] | BAHK C J,PARKER R G.Analytical investigation of tooth profile modification effects on planetary gear dynamics[J].Mechanism and Machine Theory,2013,70:298-319. |
| Click to display the text | |
| [7] |
孙建国,林腾蛟,李润方,等.渐开线齿轮动力接触有限元分析及修形影响[J].机械传动,2008,32(2):57-59. SUN Jian-guo,LIN Teng-jiao,LI Run-fang,et al.Dynamic contact finite element analysis and modification effects of involute gears[J].Journal of Mechanical Transmission,2008,32(2):57-59. |
| Cited By in Cnki (48) | Click to display the text | |
| [8] |
吴勇军,王建军,韩勤锴,等.基于接触有限元分析的斜齿轮齿廓修形与实验[J].航空动力学报,2011,26(2):409-414. WU Yong-jun,WANG Jian-jun,HAN Qin-kai,et al.Tooth profile modification of helical gears and experimental study based on finite element contact analysis[J].Journal of Aerospace Power,2011,26(2):409-414. |
| Cited By in Cnki (28) | Click to display the text | |
| [9] |
林腾蛟,沈亮,赵俊渝.风电增速箱输出级齿轮副疲劳寿命有限元分析[J].重庆大学学报,2012,35(1):1-6. LIN Teng-jiao,SHEN Liang,ZHAO Jun-yu.Fatigue life finite element analysis of output gear pair of wind turbine speed-increase gearbox[J].Journal of Chongqing University,2012,35(1):1-6. |
| Cited By in Cnki (16) | Click to display the text | |
| [10] |
王丹,陆瑞成,闫玉涛,等.航空发动机齿轮接触分析与修形研究[J].东北大学学报(自然科学版),2013,34(8):1171-1174. WANG Dan,LU Rui-cheng,YAN Yu-tao,et al.Modification research and contact analysis of aero-engine gears[J].Journal of Northeastern University (Natural Science),2013,34(8):1171-1174. |
| Cited By in Cnki (3) | Click to display the text | |
| [11] |
陈思雨,唐进元,王志伟,等.修形对齿轮系统动力学特性的影响规律[J].机械工程学报,2014,50(13):59-65. CHEN Si-yu,TANG Jin-yuan,WANG Zhi-wei,et al.Effect of modification on dynamic characteristics of gear transmissions system[J].Journal of Mechanical Engineering,2014,50(13):59-65. |
| Cited By in Cnki (1) | Click to display the text | |
| [12] |
马辉,逄旭,宋溶泽,等.考虑齿顶修缘的齿轮-转子系统振动响应分析[J].机械工程学报,2014,50(7):39-45. MA Hui,PANG Xu,SONG Rong-ze,et al.Vibration response analysis of a geared rotor system considering the tip relief[J].Journal of Mechanical Engineering,2014,50(7):49-55. |
| Cited By in Cnki (2) | Click to display the text | |
| [13] |
唐进元.齿轮传递误差计算新模型[J].机械传动,2008,32(6):13-14. TANG Jin-yuan.Gear transmission error calculation new model[J].Mechanical Transmission,2008,32(6):13-14. |
| Cited By in Cnki (23) | |
| [14] |
汪中厚,王杰,王巧玲,等.基于有限元法的螺旋锥齿轮传动误差研究[J].振动与冲击,2014,33(14):165-170. WANG Zhong-hou,WANG Jie,WANG Qiao-ling,et al.Transmission error of spiral bevel gear based on finite element method[J].Journal of Vibration and Shock,2014,33(14):165-170. |
| Cited By in Cnki | Click to display the text | |
| [15] | BONORI G,BARBIERI M,PELLICANO M.Optimum profile modifications of spur gears by means of genetic algorithms[J].Journal of Sound and Vibration,2008,313(3):603-616. |
| Click to display the text | |
| [16] | 苏华礼,秦保军.基于遗传算法的散热器优化设计[J].工程设计学报,2007,14(1):31-34. |
| Cited By in Cnki (7) | |
| [17] | 吴晓君,郑超,路超,等.基于遗传算法和ADAMS的麦弗逊悬架优化研究[J].工程设计学报,2012,19(4):74-77. |
| Cited By in Cnki (8) | |
| [18] | 蒋进科,方宗德,卞翔.人字齿轮齿向修形优化设计[J].哈尔滨工业大学学报,2013,45(11):86-92. |
| Cited By in Cnki (1) |



