2. 奇瑞新能源汽车技术有限公司, 安徽 芜湖 241000
2. Chery New Energy Automotive Technology Co., Ltd., Wuhu 241000, China
载运工具的垂向振动频率为4~8 Hz时,乘员会感到不适[1],甚至会引发交通事故或致人受伤[2]。对载运工具乘员的动态舒适性[3]进行研究是提高载运工具乘坐和驾驶舒适性的重要途径。研究乘员动态舒适性多采用试验的方法,以乘员的主观感受为评价标准。然而,这种方法不仅耗时、费力及成本高,而且主观程度高、量化程度低。若能够通过合理的手段建立可信度高的乘员人体动力学模型,就可以用软件仿真的方法指导工程设计,缩短研发周期、降低成本,为载运工具乘员的动态舒适性的研究提供方便。
坐姿人体的动力学响应是评价载运工具乘员动态舒适性的一个重要的评价标准。由质量、刚度、阻尼等机械系统的参数所构成的常微分方程或常差分方程来描述人体系统的集中参数模型[4-19],其使用了简单的机械元件,具有建模简单、分析简便、成本低、参数辨识容易、实验验证容易等优点。
1995年,Wan等采用一种四自由度混联线性模型来描述振动激励情况下坐姿人体的动力学特性[10],Liu等[11]和Abbas等[12]分别对其进行了非线性化的优化和使用加权遗传算法的模型参数优化。Singh等将Liu等提出的结构中躯干和盆骨间不连续弹簧模型进行调整,并用于研究人在直升飞机着陆时人体受到的冲击响应[13]。1998年,Boileau等对坐姿人体动力学响应的实验数据进行了系统的总结[14],并提出了一种四自由度串联线性模型[15]。张鄂等[16]对Boileau等提出的四自由度串联线性模型进行了参数优化。Liang等对比并评价了不同自由度情况下的12种坐姿人体集中参数模型的效果[2],并推荐使用由Wan等提出的四自由度混联线性模型[10],四自由度模型参数数量适中,对数据的表征也相对完善,同时也方便研究者进行以四自由度模型为基础的提高自由度数量的扩展工作。
本文提出一种拟合精度更好的坐姿人体四自由度集中参数模型,进行了基于多目标函数协调优化原理的模型参数辨识,并与经典的四自由度集中参数模型进行了对比。基于提出的模型,建立了一种“人-椅-车”七自由度模型,量化评价了汽车在不同行驶路面情况下坐姿人体的动力学响应。
1 坐姿人体四自由度集中参数模型 1.1 模型的结构与数学建模图 1是本文提出的具有14个参数的坐姿人体四自由度集中参数模型。如图 1所示,坐姿人体可看作弹簧-阻尼-质量系统,即将人体等效为弹簧、阻尼、质量三种机械元件的混合连接。根据图 1和牛顿第二定律,模型的动力学方程可以表示为:
| $ {\mathit{\boldsymbol{M}}_1}\mathit{\boldsymbol{\ddot z}} + {\mathit{\boldsymbol{C}}_1}\mathit{\boldsymbol{\dot z}} + {\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{f}}_{z1}} $ | (1) |
| $ {\mathit{\boldsymbol{M}}_1} = \left[ {\begin{array}{*{20}{c}} {{m_1}}&0&0&0\\ 0&{{m_2}}&0&0\\ 0&0&{{m_3}}&0\\ 0&0&0&{{m_4}} \end{array}} \right] $ | (2a) |
| $ {\mathit{\boldsymbol{C}}_1} = \left[ {\begin{array}{*{20}{c}} {{c_{14}}}&0&0&{ - {c_{14}}}\\ 0&{{c_{23}} + {c_{34}}}&{ - {c_{23}}}&{ - {c_{24}}}\\ 0&{ - {c_{23}}}&{{c_{23}} + {c_{24}}}&{ - {c_{34}}}\\ { - {c_{14}}}&{ - {c_{24}}}&{ - {c_{34}}}&{{c_{34}} + {c_{40}} + {c_{14}} + {c_{24}}} \end{array}} \right] $ | (2b) |
| $ {\mathit{\boldsymbol{K}}_1} = \left[ {\begin{array}{*{20}{c}} {{k_{14}}}&0&0&{ - {k_{14}}}\\ 0&{{k_{23}} + {k_{34}}}&{ - {k_{23}}}&{ - {k_{24}}}\\ 0&{ - {k_{23}}}&{{k_{23}} + {k_{24}}}&{ - {k_{34}}}\\ { - {k_{14}}}&{ - {k_{24}}}&{ - {k_{34}}}&{{k_{34}} + {k_{40}} + {k_{14}} + {k_{24}}} \end{array}} \right] $ | (2c) |
| $ {\mathit{\boldsymbol{f}}_{z1}} = \left\{ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{c_{40}}{{\dot z}_0} + {k_{40}}{z_0}} \end{array}} \right\} $ | (2d) |
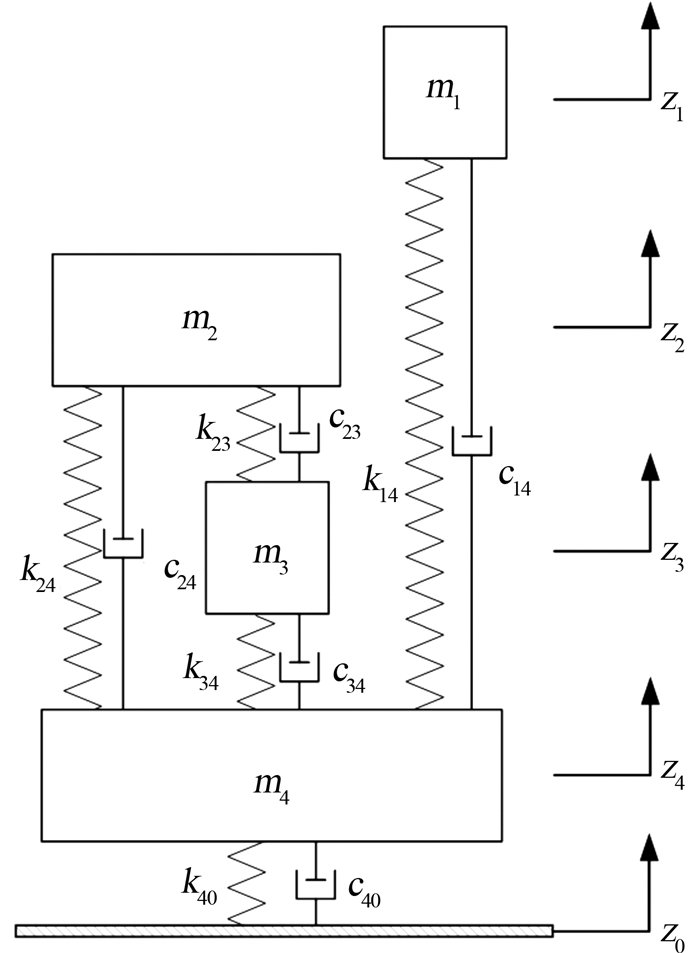
|
| 图 1 坐姿人体四自由度集中参数模型 Fig.1 The proposed 4DOF lumped-parameter model for seated human |
式中: M1表示四阶质量矩阵;C1表示四阶阻尼矩阵;K1表示四阶刚度矩阵;fz1表示激励的力向量;z =[z1, z2, z3, z4]T,
对式(1)进行傅里叶变换:
| $ \left[ {{\mathit{\boldsymbol{M}}_1}\left( { - {\omega ^2}} \right) + {\mathit{\boldsymbol{C}}_1}\left( {{\rm{j}}\omega } \right) + {\mathit{\boldsymbol{K}}_1}} \right]\mathit{\boldsymbol{Z}}\left( {{\rm{j}}\omega } \right) = {\mathit{\boldsymbol{F}}_{z1}}\left( {{\rm{j}}\omega } \right) $ | (3) |
式中:
Z(jω)和Fz1(jω)分别为:
| $ \mathit{\boldsymbol{Z}}\left( {{\rm{j}}\omega } \right) = {\left[ {{\mathit{\boldsymbol{Z}}_1}\left( {{\rm{j}}\omega } \right),{\mathit{\boldsymbol{Z}}_2}\left( {{\rm{j}}\omega } \right),{\mathit{\boldsymbol{Z}}_3}\left( {{\rm{j}}\omega } \right),{\mathit{\boldsymbol{Z}}_4}\left( {{\rm{j}}\omega } \right)} \right]^{\rm{T}}} $ | (4a) |
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_{z1}}\left( {{\rm{j}}\omega } \right) = {\left[ {0,0,0,\left( {{k_{40}} + {\rm{j}}\omega {c_{40}}} \right){\mathit{\boldsymbol{Z}}_0}\left( \omega \right)} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ 0&0\\ {{k_{40}}}&{{c_{40}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1\\ {{\rm{j}}\omega } \end{array}} \right]{\mathit{\boldsymbol{Z}}_0}\left( \omega \right) \end{array} $ | (4b) |
联立式(3)和式(4),Z(jω)可改写为:
| $ \mathit{\boldsymbol{Z}}\left( {{\rm{j}}\omega } \right) = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} 1\\ {{\rm{j}}\omega } \end{array}} \right]{\mathit{\boldsymbol{Z}}_0}\left( \omega \right) $ | (5) |
式(5)中矩阵A和B分别为:
| $ \mathit{\boldsymbol{A}} = \left[ { - {\omega ^2}{\mathit{\boldsymbol{M}}_1} + {\rm{j}}\omega {\mathit{\boldsymbol{C}}_1} + {\mathit{\boldsymbol{K}}_1}} \right] $ | (6a) |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ 0&0\\ {{k_{40}}}&{{c_{40}}} \end{array}} \right] $ | (6b) |
ISO5982—2001[20]提供了坐姿人体的3个评价指标:椅-头传递率(seat-to-head transmissibility, STHT)、驱动点机械阻抗(driving-point mechanical impedance, DPMI)和视在质量(apparent mass, AM)。
STHT为头部位移与座椅激励的位移之比,是一种无量纲的复数量,由式(5)可得:
| $ {\rm{STHT}}\left( {{\rm{j}}\omega } \right) = \frac{{{\mathit{\boldsymbol{Z}}_1}\left( {{\rm{j}}\omega } \right)}}{{{\mathit{\boldsymbol{Z}}_0}\left( \omega \right)}} = \left[ {1,0,0,0} \right]{\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} 1\\ {{\rm{j}}\omega } \end{array}} \right] $ | (7) |
DPMI为驱动点的激励力与驱动点的速度之比:
| $ \begin{array}{l} {\rm{DPMI}}\left( {{\rm{j}}\omega } \right) = \frac{{{\mathit{\boldsymbol{F}}_4}\left( \omega \right)}}{{{\mathit{\boldsymbol{v}}_4}\left( \omega \right)}} = \frac{{{k_{40}} + {\rm{j}}\omega {c_{40}}}}{{{\rm{j}}\omega }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {1 - \left[ {0,0,0,1} \right]{\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} 1\\ {{\rm{j}}\omega } \end{array}} \right]} \right] \end{array} $ | (8) |
式中: F4(jω)为驱动点激励力;v4(jω)为驱动点速度。
AM为驱动点的激励力与驱动点的加速度之比:
| $ \begin{array}{l} {\rm{AM}}\left( {{\rm{j}}\omega } \right) = \frac{{{\mathit{\boldsymbol{F}}_4}\left( {{\rm{j}}\omega } \right)}}{{{\mathit{\boldsymbol{a}}_4}\left( {{\rm{j}}\omega } \right)}} = \frac{{{k_{40}} + {\rm{j}}\omega {c_{40}}}}{{ - {\omega ^2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {1 - \left[ {0,0,0,1} \right]{\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} 1\\ {{\rm{j}}\omega } \end{array}} \right]} \right] \end{array} $ | (9) |
式中a4(jω)为驱动点加速度。
2 坐姿人体四自由度集中参数模型参数辨识 2.1 实验数据Boileau等根据测试得到0~20 Hz垂直振动激励下坐姿人体的STHT, DPMI和AM的实验数据[14],如表 1所列,被广泛用于坐姿人体多自由度模型研究。本文也将使用该数据进行坐姿人体四自由度集中参数模型的参数辨识。
| 频率/Hz | STHT | DPMI/(Ns/m) | AM/kg |
| 0.5 | 1.01 | 254 | 61.2 |
| 0.63 | 1.01 | 304 | 61.4 |
| 0.80 | 1.01 | 359 | 60.6 |
| 1.0 | 1.02 | 424 | 59.6 |
| 1.25 | 1.03 | 493 | 59.2 |
| 1.6 | 1.06 | 627 | 60.0 |
| 2.0 | 1.08 | 768 | 60.8 |
| 2.5 | 1.10 | 947 | 62.6 |
| 3.15 | 1.16 | 1 429 | 70.7 |
| 4.0 | 1.29 | 2 002 | 79.3 |
| 5.0 | 1.45 | 2 346 | 74.5 |
| 6.3 | 1.23 | 2 065 | 53.2 |
| 8.0 | 1.01 | 1 939 | 38.5 |
| 10.0 | 0.96 | 1 981 | 31.5 |
| 12.5 | 0.86 | 2 023 | 25.9 |
| 16.0 | 0.71 | 1 750 | 17.4 |
| 20.0 | 0.63 | 1 755 | 14.1 |
坐姿人体四自由度集中参数模型的参数辨识需要同时考虑模型参数对STHT,DPMI和AM三个目标函数的影响,属于一种多目标优化问题。在这类问题中,多个目标通常会相互影响和相互冲突,所以要对目标进行权衡和折中[21]。多目标优化问题并不存在唯一的最优解,而是存在一组最优解集,称为Pareto前沿面。基于Pareto优化原理的遗传算法在处理多目标优化时可以获得Pareto前沿面。基于非支配排序的带有精英策略的多目标优化算法(NSGA-Ⅱ算法)是一种基于Pareto优化原理的遗传算法[22],该算法具有搜索非劣解迅速、收敛速度快、非劣解分布范围广的特点。
2.3 多目标函数及边界条件如表 1所列,STHT,DPMI和AM的实验值是随着激励频率的变化而变化的。结合式(7)至式(9)可以计算出相应四自由度集中参数模型的STHT,DPMI和AM的仿真值。优化目标函数是一个三维行向量,分别代表STHT,DPMI和AM仿真值与实验值的方差。基于坐姿人体的基本参数[23]:人体头颈部质量占总质量(75.4 kg)的8.4%,将边界条件的上限与下限扩展到实际质量的10%;座椅承载人体的质量占人体总质量的73.6%,即55.5 kg。根据对人体解剖所得的数据[24],人体各个结构的刚度值在100~300 000 N/m之间,而根据实验建议人体各个结构的阻尼值在500~4 000 Ns/m之间[25]。
多目标函数可以表示为:
| $ \min {F_{{\rm{cn}}}} = {\left[ \begin{array}{l} \sum\limits_{i = 1}^{{\rm{Num}}} {{{\left( {{\rm{STHT}}\left( {{f_i}} \right) - {\rm{STH}}{{\rm{T}}_0}\left( {{f_i}} \right)} \right)}^2}} \\ \sum\limits_{i = 1}^{{\rm{Num}}} {{{\left( {{\rm{DPMI}}\left( {{f_i}} \right) - {\rm{DPM}}{{\rm{I}}_0}\left( {{f_i}} \right)} \right)}^2}} \\ \sum\limits_{i = 1}^{{\rm{Num}}} {{{\left( {{\rm{AM}}\left( {{f_i}} \right) - {\rm{A}}{{\rm{M}}_0}\left( {{f_i}} \right)} \right)}^2}} \end{array} \right]^{\rm{T}}} $ | (10a) |
边界条件为:
| $ \left\{ \begin{array}{l} 5.31 \le {m_1} \le 6.49{\rm{kg}}\\ {m_1} + {m_2} + {m_3} + {m_4} = 55.5{\rm{kg}}\\ 100 \le {k_n} \le 300\ 000{\rm{N/m}}\\ 500 \le {c_n} \le 4\ 000{\rm{Ns/m}} \end{array} \right. $ | (10b) |
式中:Num表示实验数据点的总数;f表示激励频率;STHT(fi),DPMI(fi)和AM(fi)分别表示STHT, DPMI和AM在第i个激励频率时的仿真值;STHT0(fi),DPMI0(fi)和AM0(fi)分别表示STHT, DPMI和AM在第i个激励频率时的实验值。
2.4 参数辨识的结果与评价为量化分析单个目标函数和综合目标函数的辨识结果的优劣,使用拟合优度ε[26]和综合拟合优度ε来评价参数辨识的结果。
| $ \varepsilon = 1 - \frac{{\sqrt {\sum {{{\left( {{\tau _{\rm{m}}}/{\tau _{\rm{c}}}} \right)}^2}/\left( {N - 2} \right)} } }}{{\sum {\left( {{\tau _{\rm{m}}}/N} \right)} }} $ | (11a) |
| $ \bar \varepsilon = \frac{1}{3}\left( {{\varepsilon _{{\rm{STHT}}}} + {\varepsilon _{{\rm{DPMI}}}} + {\varepsilon _{{\rm{AM}}}}} \right) $ | (11b) |
式中:τm是实验值, τc是仿真值;εSTHT, εDPMI和εAM分别表示STHT, DPMI和AM的拟合优度。
ε和ε的值可以表示模型的仿真值与实验值的一致程度,取值范围为[0, 1],越接近于1,拟合效果越好。基于NSGA-Ⅱ算法实现的多目标函数优化的结果可得Pareto最优前沿面上最大综合拟合优度εmax=0.918 6。此时,εSTHT, εDPMI和εAM分别为0.929,0.908和0.919,对应的坐姿人体四自由度模型的各个参数值如表 2所示。
| 模型 | 质量/kg | 刚度/(103 N/m) | 阻尼/(102 Ns/m) | |||||||||||||||||
| m1 | m2 | m3 | m4 | k1 | k2 | k3 | k4 | k13 | k14 | k24 | c1 | c2 | c3 | c4 | c13 | c14 | c24 | |||
| 本文模型 | 6.142 | 8.578 | 20.59 | 17.79 | 22.74 | 20.41 | 92.75 | 59.19 | 22.28 | 18.51 | 8.456 | 23.58 | 9.497 | 8.619 | ||||||
| Wan等的模型 | 4.170 | 15.00 | 5.500 | 36.00 | 134.4 | 10.00 | 20.00 | 49.34 | 192.0 | 2.500 | 2.000 | 3.300 | 24.75 | 9.091 | ||||||
| Abbas等的模型 | 4.170 | 15.00 | 5.500 | 36.00 | 167.0 | 10.00 | 20.00 | 49.34 | 144.0 | 3.100 | 2.000 | 3.300 | 24.75 | 9.091 | ||||||
| Boileau等的模型 | 5.310 | 8.620 | 28.49 | 12.78 | 183.0 | 90.00 | 310.0 | 162.8 | 47.50 | 20.64 | 4.000 | 45.85 | ||||||||
| 张鄂等的模型 | 5.310 | 10.45 | 24.14 | 15.60 | 150.1 | 70.04 | 310.0 | 111.5 | 40.00 | 26.98 | 40.00 | 40.00 | ||||||||
近年来,对坐姿人体四自由度模型的研究十分广泛,但是这些模型多为基于Wan等提出的四自由度混联线性模型(以下简称“ Wan等的模型”,如图 2(a))和Boileau等提出的四自由度串联模型(以下简称“ Boileau等的模型”,如图 2(b))的结构或参数上的优化[10, 27]。本文将2种经典模型及其参数优化后的模型作为提出的模型的对比对象。表 2列出了本文提出的模型与经典模型及其参数优化后模型的参数值[15, 10, 12, 27]。
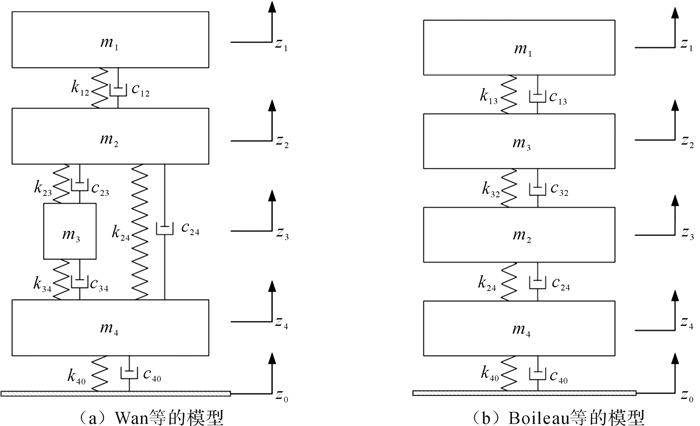
|
| 图 2 模型对比 Fig.2 Comparison of models |
如图 3所示,对比的5种坐姿人体四自由度模型的STHT,DPMI和AM曲线均与实验测试结果保持一定的一致性,表明这些模型均能大致描述坐姿人体的动力学响应。为量化比较各种模型的性能,结合图 3和式(11),图 4给出了5种模型的STHT, DPMI和AM的拟合优度ε和最大综合拟合优度εmax的对比。
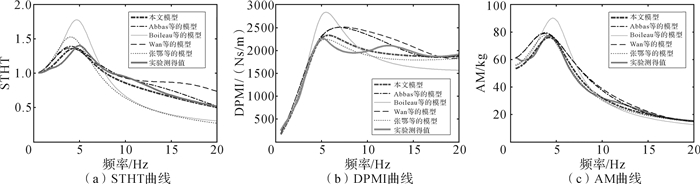
|
| 图 3 各模型的STHT,DPMI,AM曲线比较 Fig.3 Comparison of STHT, DPMI, AM curves of the models |
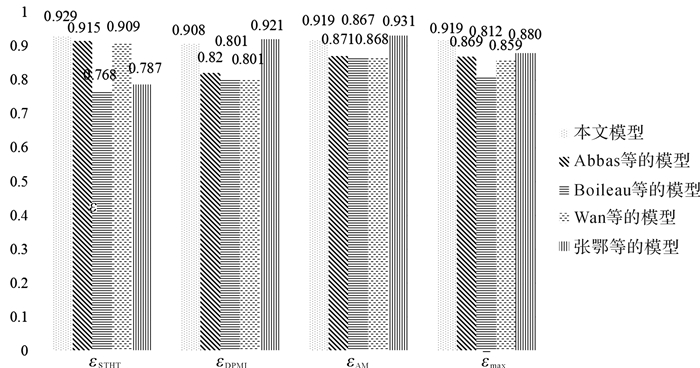
|
| 图 4 本文提出的模型与典型模型的拟合优度及综合拟合优度的比较 Fig.4 The goodnesses of fit in profiles of STHT, DPMI, and AM and maximal comprehensive goodnesses of fit of the proposed model and the classic models |
Wan等的模型和Boileau等的模型相比较而言,也各有一些不足。Wan等的模型在拟合DPMI时的效果比较差(εDPMI=0.801),Boileau等的模型在拟合STHT时效果非常差(εSTHT=0.768),在拟合DPMI时的效果也比较差(εDPMI=0.801)。这表明Wan等的模型和Boileau等的模型均有很大的改进空间。
总的来说,本文提出的模型比经典的4种四自由度模型对实验测试结果的拟合程度更高(其最大综合拟合优度最大,εmax=0.919)。在STHT,DPMI和AM的拟合优度方面,提出的模型相对Abbas等、Boileau等以及Wan等的模型有所提高;相对张鄂等的模型,本文提出的模型在STHT上的拟合优度也有非常显著的提高(εSTHT提高了0.142),而在DPMI和AM上的拟合优度略有降低(εDPMI降低了0.013,εAM降低了0.012)。
综合以上:1)相对于经典的坐姿人体四自由度模型,本文提出的集中参数模型能够更好地拟合实验测试结果;2)针对多目标优化问题,基于Pareto优化原理并使用NSGA-Ⅱ算法进行坐姿人体四自由度集中参数辨识方法是有效的。
4 “人-椅-车”七自由度集中参数模型 4.1 “人-椅-车”模型的结构与数学建模为了进一步验证和评价所提出的坐姿人体四自由度集中参数模型在整车上的应用,建立的“人-椅-车”七自由度集中参数模型,如图 5所示。根据图 5,结合牛顿第二定律,“人-椅-车”七自由度模型的动力学方程可表示为:
| $ {\mathit{\boldsymbol{M}}_2}{{\mathit{\boldsymbol{\ddot z}}}_{\rm{a}}} + {\mathit{\boldsymbol{C}}_2}{{\mathit{\boldsymbol{\dot z}}}_{\rm{a}}} + {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{z}}_{\rm{a}}} = {\mathit{\boldsymbol{f}}_{z2}} $ | (12) |
| $ {\mathit{\boldsymbol{M}}_2} = \left[ {\begin{array}{*{20}{c}} {{m_1}}&0&0&0&0&0&0\\ 0&{{m_2}}&0&0&0&0&0\\ 0&0&{{m_3}}&0&0&0&0\\ 0&0&0&{{m_4}}&0&0&0\\ 0&0&0&0&{{m_{\rm{s}}}}&0&0\\ 0&0&0&0&0&{{m_{\rm{c}}}}&0\\ 0&0&0&0&0&0&{{m_{\rm{w}}}} \end{array}} \right] $ | (13a) |
| $ {\mathit{\boldsymbol{C}}_2} = \left[ {\begin{array}{*{20}{c}} {{c_{14}}}&0&0&{ - {c_{14}}}&0&0&0\\ 0&{{c_{23}} + {c_{24}}}&{ - {c_{23}}}&{ - {c_{24}}}&0&0&0\\ 0&{ - {c_{23}}}&{{c_{23}} + {c_{34}}}&{ - {c_{34}}}&0&0&0\\ { - {c_{14}}}&{ - {c_{24}}}&{ - {c_{34}}}&{{c_{34}} + {c_{4{\rm{s}}}} + {c_{14}} + {c_{24}}}&{ - {c_{4{\rm{s}}}}}&0&0\\ 0&0&0&{ - {c_{4{\rm{s}}}}}&{{c_{4{\rm{s}}}} + {c_{\rm{s}}}}&{ - {c_{\rm{s}}}}&0\\ 0&0&0&0&{ - {c_{\rm{s}}}}&{{c_{\rm{s}}} + {c_{\rm{c}}}}&{ - {c_{\rm{c}}}}\\ 0&0&0&0&0&{ - {c_{\rm{c}}}}&{{c_{\rm{c}}} + {c_{\rm{w}}}} \end{array}} \right] $ | (13b) |
| $ {\mathit{\boldsymbol{K}}_2} = \left[ {\begin{array}{*{20}{c}} {{k_{14}}}&0&0&{ - {k_{14}}}&0&0&0\\ 0&{{k_{23}} + {k_{24}}}&{ - {k_{23}}}&{ - {k_{24}}}&0&0&0\\ 0&{ - {k_{23}}}&{{k_{23}} + {k_{34}}}&{ - {k_{34}}}&0&0&0\\ { - {k_{14}}}&{ - {k_{24}}}&{ - {k_{34}}}&{{k_{34}} + {k_{4{\rm{s}}}} + {k_{14}} + {k_{24}}}&{ - {k_{4{\rm{s}}}}}&0&0\\ 0&0&0&{ - {k_{4{\rm{s}}}}}&{{k_{4{\rm{s}}}} + {k_{\rm{s}}}}&{ - {k_{\rm{s}}}}&0\\ 0&0&0&0&{ - {k_{\rm{s}}}}&{{k_{\rm{s}}} + {k_{\rm{c}}}}&{ - {k_{\rm{c}}}}\\ 0&0&0&0&0&{ - {k_{\rm{c}}}}&{{k_{\rm{c}}} + {k_{\rm{w}}}} \end{array}} \right] $ | (13c) |
| $ {\mathit{\boldsymbol{f}}_{z2}} = \left\{ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ {{k_w}{z_0}} \end{array}} \right\} $ | (13d) |
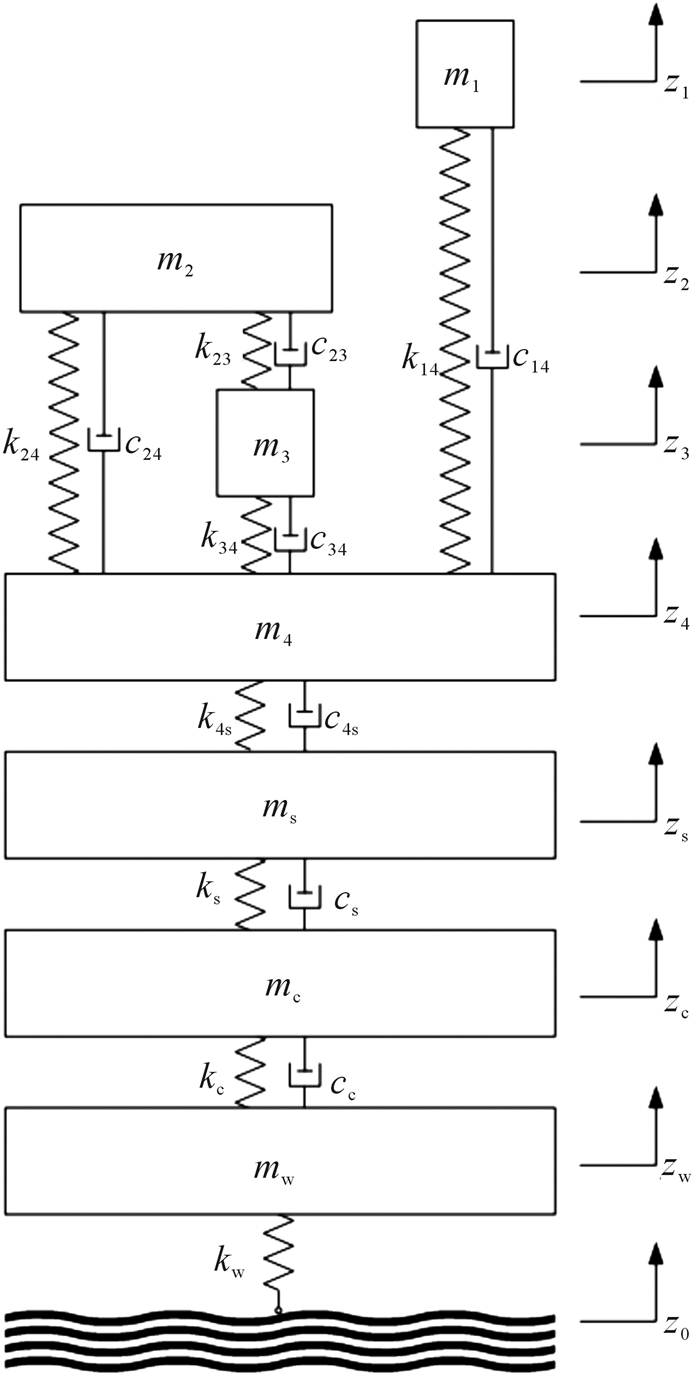
|
| 图 5 “人-椅-车”七自由度集中参数模型 Fig.5 A "human-seat-automobile" 7DOF lumped-parameter model |
式中: za,
基于功率谱的滤波白噪声生成方法实现不确定的路面工况:
| $ {G_{\rm{q}}}\left( n \right) = {G_{\rm{q}}}\left( {{n_0}} \right){\left( {\frac{{{n_{\rm{a}}}}}{{{n_0}}}} \right)^{ - {\omega _1}}} $ | (14) |
式中:Gq(n)为功率谱密度;na为每米的水平距离所有的振幅波的数量,即水平距离频率;n0为水平距离频率的基准;Gq(n0)为路面不平度系数;ω1为频率指数, 为双对数坐标上斜线的斜率,它决定路面功率谱密度的频率结构。
“人-椅-车”七自由度模型中的人体参数使用第3节提出的模型的辨识结果,座椅和车的参数取自某款普通轿车,如表 3所示。
| 参数 | 数值 |
| m1/kg | 6.142 |
| m2/kg | 8.578 |
| m3/kg | 20.59 |
| m4/kg | 17.79 |
| ms/kg | 35 |
| mc/kg | 250 |
| mw/kg | 35 |
| k23/(N/m) | 22 740 |
| k34/(N/m) | 204 100 |
| k4s/(N/m) | 92 750 |
| k14/(N/m) | 59 190 |
| k24/(N/m) | 22 280 |
| ks/(N/m) | 15 000 |
| kc/(N/m) | 16 000 |
| kw/(N/m) | 160 000 |
| c23/(Ns/m) | 1 851 |
| c34/(Ns/m) | 845.6 |
| c4s/(Ns/m) | 2 358 |
| c14/(Ns/m) | 949.7 |
| c24/(Ns/m) | 861.9 |
| cs/(Ns/m) | 150 |
| cc/(Ns/m) | 980 |
| cw/(Ns/m) | 0 |
基于MATLAB/Simulink建立的“人-椅-车”七自由度模型,取行驶速度为30, 50和70 km/h, 仿真路面等级为B级、C级和D级,组合成9种工况进行仿真分析,得到了坐姿人体头部和臀部的动力学响应。图 6、图 7和图 8分别给出了行驶速度为30 km/h时不同路面等级情况下坐姿人体加速度响应,B级路面时不同行驶速度情况下坐姿人体加速度响应和B级路面、行驶速度为30 km/h情况下坐姿人体头部与臀部加速度。
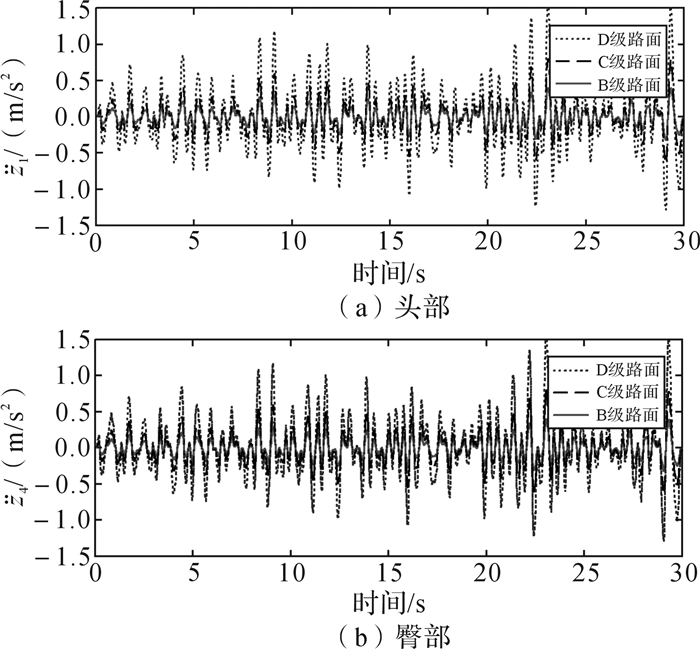
|
| 图 6 行驶速度为30 km/h时不同路面等级情况下坐姿人体加速度响应 Fig.6 Acceleration responses of seated human under different types of road with automotive speed of 30 km/h |
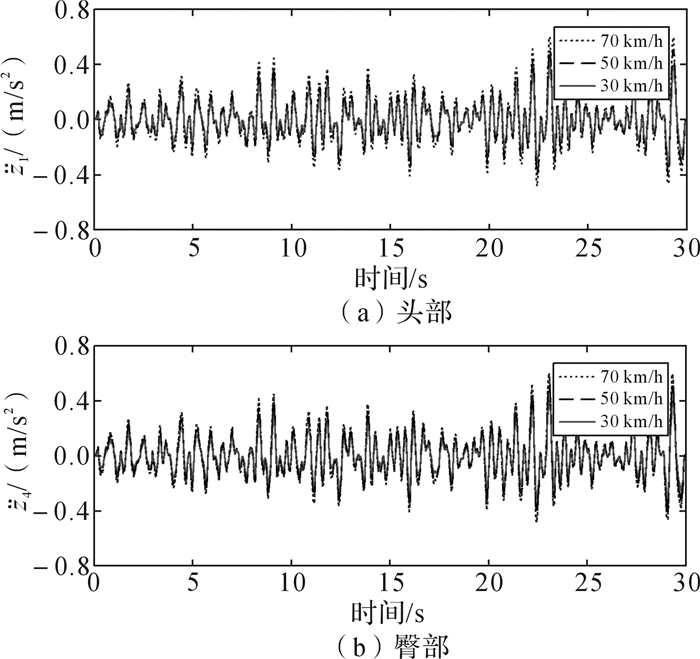
|
| 图 7 B级路面时不同行驶速度情况下坐姿人体加速度响应 Fig.7 Acceleration responses of seated human under different automotive speeds with B type of road |

|
| 图 8 B级路面、30 km/h行驶速度情况下坐姿人体头部与臀部加速度响应 Fig.8 Acceleration responses of head and bottom of seated human when on B-level road and at 30 km/h automotive speed |
如图 6(a)和6(b)所示,路面等级的变化会对坐姿人体的动力学响应造成影响。路面条件越差,人体头部和臀部的加速度越高,这表明了粗糙不平的路面会加重人体的动力学响应,造成人体的不适。如图 7(a)和7(b)所示,汽车的行驶速度也会对坐姿人体的动力学响应造成影响。汽车的行驶速度越高,人体头部和臀部的加速度越高,这表明了行驶速度的提高也会加重人体的动力学响应,造成人体的不适。此外,路面等级和汽车行驶速度会同时影响人体的动力学响应。路面等级从B降低到C时比行驶速度从30 km/h提升到70 km/h时人体头部和臀部的加速度的变化率更高,说明路面等级对人体的动力学响应的影响程度更高。
根据图 6和图 7,人体头部和臀部的加速度值在各种行驶工况下相差并不明显。如图 8所示,人体头部和臀部的加速度值相比,头部的值略微高一些。
4.4 人体垂向均方根加速度为量化坐姿人体的动力学响应,采用ISO2631-1—1997来评价汽车平顺性和乘员的乘坐舒适性。垂向方向的均方根加速度az是由加速度的功率谱密度计算而得:
| $ {a_{\rm{z}}} = {\left[ {\int_{0.5}^{80} {\omega _2^2\left( f \right){G_a}\left( f \right){\rm{d}}f} } \right]^{\frac{1}{2}}} $ | (15) |
式中:ω22(f)为频率加权函数;Ga(f)为加速度的功率谱密度函数。
对于ω22(f)为频率加权函数,有:
| $ {\omega _2}\left( f \right) = \left\{ \begin{array}{l} 0.5,\;\;\;\;0.5 < f < 2{\rm{Hz}}\\ f/4,\;\;2 < f < 4{\rm{Hz}}\\ 1,\;\;\;\;\;\;\;4 < f < 12.5{\rm{Hz}}\\ 12.5,\;\;12.5 < f < 80{\rm{Hz}} \end{array} \right. $ | (16) |
根据式(15)和式(16)可以求得人体的垂向加速度功率谱密度,如图 9所示,人体承受振动时的主观感受与加权均方根加速度如表 4所列。从图 9可知,人体头部和臀部的垂向加速度功率谱密度受到路面等级和行驶速度两种因素的影响,影响的趋势与这种因素对人体头部和臀部的加速度响应的影响相同。根据图 9和表 4可知,路面情况越差,人体头部与臀部的垂向均方根加速度越大,乘员的不适程度越高。随着汽车行驶速度提高,人体头部与臀部的垂向均方根加速度增加,乘员的不适程度越高。此外,路面情况对人体头部与臀部的垂向均方根加速度的影响程度比汽车行驶速度更大,差的路面状况会使得乘员感到不舒适。乘员头部与臀部的垂向均方根加速度在相同行驶工况下的差距很小,并且头部的垂向均方根加速度的值略高。
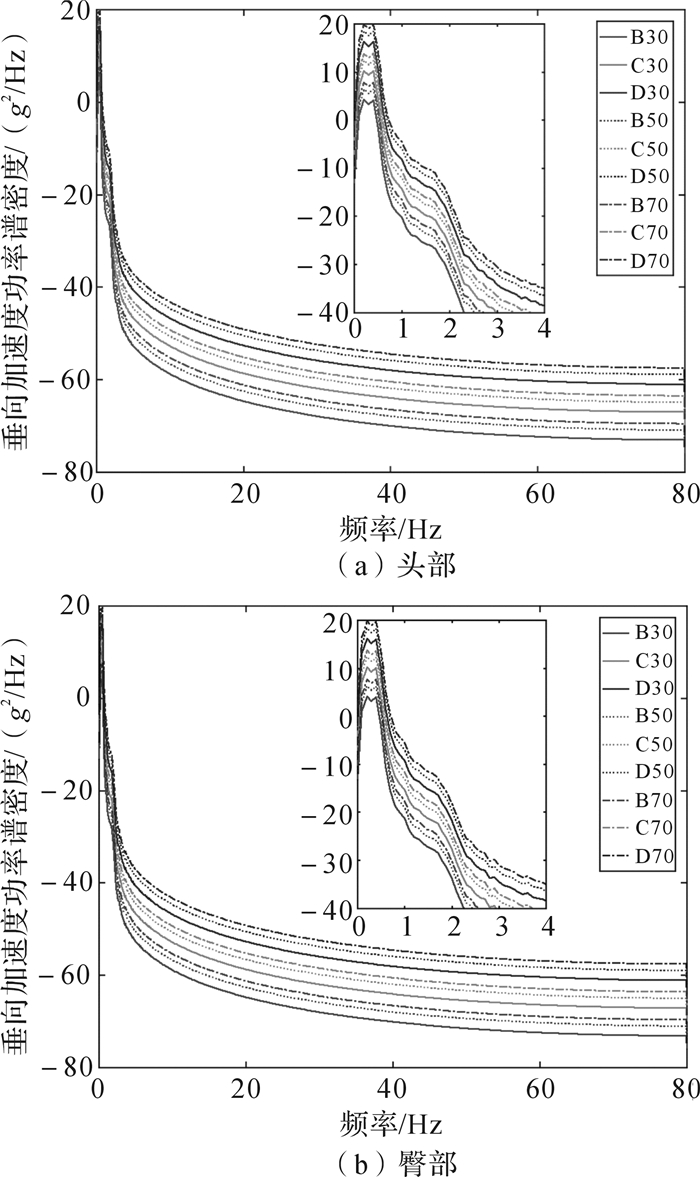
|
| 图 9 人体垂向加速度功率谱密度曲线 Fig.9 Power spectrum density of human vertical acceleration responses |
| 路面等级 | 行驶速度/(km/h) | 垂向均方根加速度/(g2/Hz) | 主观感受 | |
| 头部 | 臀部 | |||
| B级 | 30 | 0.117 0 | 0.111 8 | 无不舒适 |
| 50 | 0.150 9 | 0.144 3 | 无不舒适 | |
| 70 | 0.178 2 | 0.170 4 | 无不舒适 | |
| C级 | 30 | 0.233 9 | 0.223 7 | 有点不舒适 |
| 50 | 0.301 7 | 0.288 5 | 有点不舒适 | |
| 70 | 0.356 5 | 0.340 9 | 有些不舒适 | |
| D级 | 30 | 0.467 9 | 0.447 4 | 有些不舒适 |
| 50 | 0.603 4 | 0.577 0 | 不舒适 | |
| 70 | 0.713 0 | 0.681 8 | 不舒适 | |
本文提出一种坐姿人体四自由度集中参数模型,基于多目标函数协调优化原理进行了模型参数辨识,并与经典的四自由度集中参数模型进行了对比和分析。同时建立了一种“人-椅-车”七自由度模型,并完成了汽车在不同行驶路面情况下坐姿人体的动力学响应的仿真实验。研究结果表明:
1) 相较于经典模型及参数优化的经典模型,提出的坐姿人体四自由度集中参数模型能够更好地拟合实验测试结果。
2) 基于Pareto优化原理,使用NSGA-Ⅱ算法进行多函数相互协调优化的坐姿人体四自由度集中参数辨识是有效的。
3) 汽车的乘坐舒适性和行驶平顺性(坐姿人体动力学响应)可以用垂向均方根加速度来进行量化评价。路面条件的恶化与汽车行驶速度的提高均会造成人体头部和臀部的加速度的提高,即加深乘员的不适程度,分析结果符合实际情况。
| [1] | International Organization for Standardization. Mechanical vibration and shock:evaluation of human exposure to whole-body vibration, Part 1:general requirements:ISO 2631-1[S]. Geneva:The Organization, 1997. |
| [2] | LIANG C C, CHIANG C F. A study on biodynamic models of seated human subjects exposed to verticalvibration[J]. International Journal of Industrial Ergonomics, 2006, 36(10): 869–890. DOI:10.1016/j.ergon.2006.06.008 |
| [3] | SIEFERT A, PANKOKE S, WÖLFEL H P, et al. Virtual optimization of car passenger seats:simulation of static and dynamic effects on drivers' seating comfort[J]. International Journal of Industrial Ergonomics, 2008, 38(5/6): 410–424. |
| [4] | COERMANN R R. The mechanical impedance of the human body in sitting and standing position at low frequencies[J]. Human Factors, 1962, 4(5): 227–253. DOI:10.1177/001872086200400502 |
| [5] | MUKSIAN R, NASH C D. On frequency-dependent damping coefficients in lumped-parameter models of human beings[J]. Journal of Biomechanics, 1976, 9(5): 339–342. DOI:10.1016/0021-9290(76)90055-5 |
| [6] | SUGGS C W, ABRAMS C F, STIKELEATHER L F, et al. Application of a damped spring-mass human vibration simulator in vibration testing of vehicle seats[J]. Ergonomics, 1969, 12(1): 79–90. DOI:10.1080/00140136908931030 |
| [7] |
冯焕玉.
两自由度人体振动模型及其在汽车平顺性试验中的应用[J]. 汽车技术, 1986, 17(5): 19–26.
FENG Huan-yu. 2DOF vibration model for human body and its application to automobile ride comfort tests[J]. Automobile Technology, 1986, 17(5): 19–26. |
| [8] |
高江华, 侯之超, 何乐, 等.
坐姿人体垂向振动特性及其两自由度模型[J]. 中国科学(技术科学), 2011, 41(12): 1640–1648.
GAO Jiang-hua, HOU Zhi-chao, HE Le, et al. Vertical vibration characteristics of seated human bodies and a biodynamic model with two degrees of freedom[J]. Scientia Sinica (Technologica), 2011, 41(12): 1640–1648. |
| [9] |
侯之超, 高江华, 何乐, 等.
坐姿人体垂向振动特性及其三自由度模型参数[J]. 哈尔滨工程大学学报, 2011, 32(9): 1223–1227.
HOU Zhi-chao, GAO Jiang-hua, HE Le, et al. Vertical vibration characteristics of seated human bodies and the parameters of a biodynamic model with three degrees of freedom[J]. Journal of Harbin Engineering University, 2011, 32(9): 1223–1227. |
| [10] | WAN Y, SCHIMMELS J M. A simple model that captures the essential dynamics of a seated human exposed to whole body vibration[J]. Advances in Bioengineering, 1995, 31: 333–334. |
| [11] | LIU X X, SHI J, LI G H, et al. Biodynamic response and injury estimation of ship personnel to ship shock motion induced by underwater explosion[C]//Proceeding of 69th Shock and Vibration Symposium. Alabama:NASA Conference Publication, 1998, 18:1-18. |
| [12] | ABBAS W, ABOUELATTA O B, EL-AZAB M, et al. Optimization of biodynamic seated human models using genetic algorithms[J]. Engineering, 2010, 2(9): 710. DOI:10.4236/eng.2010.29092 |
| [13] | SINGH H J, WERELEY N M. Biodynamic model of a seated occupant exposed to intense impacts[J]. AIAA Journal, 2014, 53(2): 426–435. |
| [14] | BOILEAU P É, WU X, RAKHEJA S, et al. Definition of a range of idealized values to characterize seated body biodynamic response under vertical vibration[J]. Journal of Sound and Vibration, 1998, 215(4): 841–862. DOI:10.1006/jsvi.1998.1674 |
| [15] | BOILEAU P É, RAKHEJA S. Whole-body vertical biodynamic response characteristics of the seated vehicle driver:measurement and model development[J]. International Journal of Industrial Ergonomics, 1998, 22(6): 449–472. DOI:10.1016/S0169-8141(97)00030-9 |
| [16] |
张鄂, 许林安, 刘中华, 等.
多自由度坐姿人体上体系统动力学建模与振动特性研究[J]. 工程设计学报, 2008, 15(4): 244–249.
ZHANG E, XU Lin-an, LIU Zhong-hua, et al. Dynamic modeling and vibration characteristics of multi-DOF upper part system of seated human body[J]. Chinese Journal of Engineering Design, 2008, 15(4): 244–249. |
| [17] | ARSLAN Y Z. Experimental assessment of lumped-parameter human body models exposed to whole body vibration[J]. Journal of Mechanics in Medicine and Biology, 2015, 15(3): 1550023. DOI:10.1142/S0219519415500232 |
| [18] | RVTZEL S, HINZ B, WÖLFEL H P, et al. Modal description:a better way of characterizing human vibration behavior[J]. Journal of Sound and Vibration, 2006, 298(3): 810–823. DOI:10.1016/j.jsv.2006.06.019 |
| [19] | International Organization for Standardization. Mechanical vibration and shock:range of idealized values to characterize seated-body biodynamic response under vertical vibration:ISO 5982-2001[S]. Geneva:The Organization, 2001. |
| [20] |
张志飞, 胡正权, 徐中明, 等.
面向振动响应特性的坐姿人体动力学模型[J]. 振动与冲击, 2016, 35(4): 104–109.
ZHANG Zhi-fei, HU Zheng-quan, XU Zhong-ming, et al. A dynamic model of a seated human body based on dynamic response[J]. Journal of Sound and Vibration, 2016, 35(4): 104–109. |
| [21] | WANG D H, BAI X X. Pareto optimization-based tradeoff between the damping force and the sensed relative displacement of a self-sensing magnetorheological damper[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(13): 1452–1467. |
| [22] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. DOI:10.1109/4235.996017 |
| [23] | PHEASANT S, HASLEGRAVE C M. Bodyspace:anthropometry, ergonomics and the design of work[M]. Boca Raton: CRC Press, 2005: 44. |
| [24] | KAZARIAN L. Dynamic response characteristics of the human vertebral column:an experimental study on human autopsy specimens[J]. Acta Orthopaedica Scandinavica, 1972, 43(Supp 146): 1–188. |
| [25] | MERTENS H. Nonlinear behavior of sitting humans under increasing gravity[J]. Aviation, Space, and Environmental Medicine, 1978, 49(1 Pt. 2): 287–298. |
| [26] | WONG J Y. Terramechanics and off-road vehicle engineering:terrain behaviour, off-road vehicle performance and design[M]. Oxford: Butterworth-heinemann, 2009: 83. |
| [27] |
张鄂, 刘中华, 邵晓春.
九自由度乘坐动力学模型的人体振动特性仿真[J]. 交通运输工程学报, 2010, 10(4): 58–64.
ZHANG E, LIU Zhong-hua, SHAO Xiao-chun. Simulation of human vibration characteristics based on 9-DOF riding dynamics model[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 58–64. |


