2. 中国石油集团 东方地球物理勘探有限责任公司, 河北 涿州 072750
2. Bureau of Geophysical Prospecting Inc., China National Petroleum Corporation, Zhuozhou 072750, China
作为一种可以激发受控地震波信号的先进勘探装备,可控震源具有高效环保等优点,越来越受到用户青睐[1-2]。作为整个装备的核心部件之一,振动器的振动特性及振动器-大地耦合情况直接影响输出信号品质,是决定油气勘探质量的关键[3-4]。徐爱军等对可控震源平板-大地振动模型及参数进行了研究,认为在扫描频带范围内可能会出现谐振[5]。Wei在Sallas模型的基础上对振动器-大地耦合模型进行研究,发现振动器平板与大地之间的接触刚度以及平板本身刚度对耦合条件有很大影响[6]。马磊等将矩阵束方法应用于可控震源振动平板模态分析,指出现有工字钢焊接而成的平板长短轴方向上的刚度存在差异[7]。Hendrix在多个加速度下分析了振动器的响应,表明振动器的变形并非与激励一致,而是复杂多向的,Dean和Wei等的研究也得到同样的结果[8-11]。振动器非激励性的变形和振动会对输出信号产生干扰,降低信号品质,必须引起重视。
国产KZ-28型可控震源作为具有我国自主知识产权的震源装备,在国内外有着广泛的使用[12-13],而目前尚未有针对其振动器系统模态特性的研究,尤其是针对非激励振动产生原因的研究,因此对其开展模态分析具有重要意义。根据KZ-28可控震源振动器的实际尺寸,建立振动器-大地模型,利用计算模态分析的相关理论,通过ANSYS Workbench有限元分析软件对其进行预应力模态分析,得到振动器的振动特性,并通过试验对仿真结果进行验证,为振动器结构的设计提供可靠的理论和试验依据。
1 有限元模态分析理论有限元模态分析[14]是以模态矩阵作为变换矩阵,将原物理坐标变换为自然坐标,使系统在原坐标下的耦合方程组变成一组互相独立的二阶常微分方程,用单自由度系统的振动方程求解,得到系统的各阶模态,再通过模态叠加,转换到原来的物理坐标。
对于具有n个自由度的多自由度振动系统,它的无阻尼自由振动方程为[15]:
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{KX}} = {\bf{0}} $ | (1) |
式中:M为结构质量矩阵;
因为固有频率和振型是系统的固有属性,与外部激励无关,所以式(1) 右端的载荷项可以忽略。对于线性多自由度系统,自由振动为简谐振动,其方程为:
| $ \mathit{\boldsymbol{X}} = {\mathit{\Phi }_i}{\rm{cos}}({\omega _i}t) $ | (2) |
式中:Φi为第i(i=1,2,3,…,n)阶固有频率对应的特征向量,即振型;ωi为第i阶固有频率;t为时间。
将式(2) 代入式(1),可得:
| $ \mathit{\boldsymbol{K}} - \omega _i^2\mathit{\boldsymbol{M}}{\mathit{\Phi }_i} = {\bf{0}} $ | (3) |
由于式(3) 是齐次线性方程组,有非零解的充要条件是:
| $ \left| {\mathit{\boldsymbol{K}} - \omega _i^2\mathit{\boldsymbol{M}}} \right| = 0 $ | (4) |
式(4) 称为特征方程,由该方程可解得特征值ωi2,将ωi2代入式(3),可求得对应的特征向量Φi。
可控震源工作时,首先将28 t自重和4 t重锤压在振动器及平板上,这将会对振动器的刚度产生影响,此时的模态分析应为有预应力的模态分析,其振动方程为:
| $ \mathit{\boldsymbol{M\ddot X}} + \left( {\mathit{\boldsymbol{K}} + \mathit{\boldsymbol{\bar Y}}} \right)\mathit{\boldsymbol{X}} = {\bf{0}} $ | (5) |
1) 实体模型的建立。
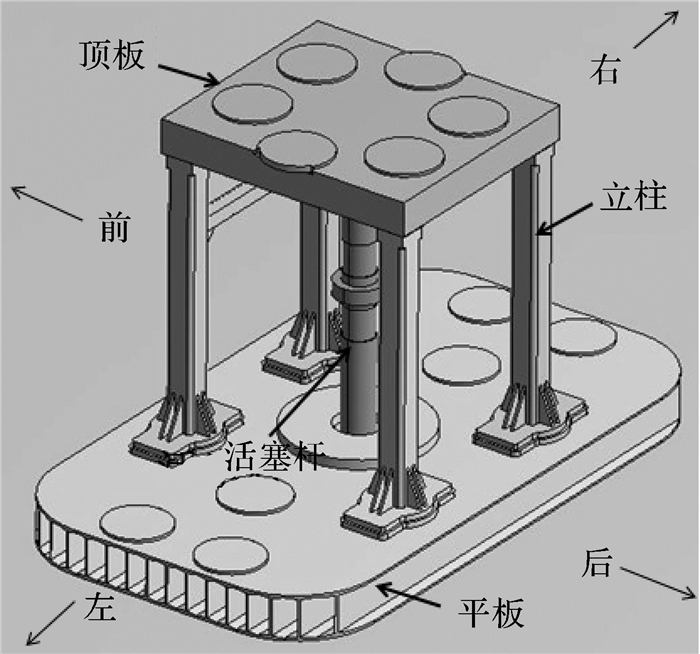
在Pro/E中,根据国产KZ-28型可控震源,忽略工艺倒角等对分析结果影响不大的特征,以1:1的比例建立振动器模型,如图 1。
|
| 图 1 振动器模型 Fig.1 Vibrator model |
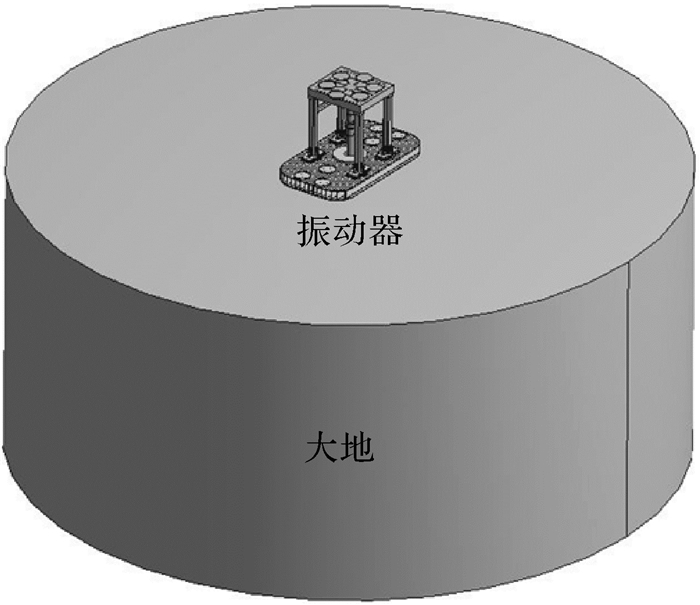
重锤在工作过程中仅提供反作用力且质量由空气弹簧补偿,因此建立的模型中对其进行了简化,其重力将在有限元分析中以压力的形式施加在空气弹簧底座上。建立的大地模型必须足够大,以包含振动器所能捕获的大地[18],这里选取直径为10 m、高度为4.5 m的圆柱体作为大地模型,建立的振动器-大地模型如图 2所示。
|
| 图 2 振动器-大地模型 Fig.2 Vibrator-ground model |
2) 材料选择与网格划分。
将建立的振动器-大地模型导入ANSYS Workbench中,定义振动器的材料为结构钢,大地的材料为混泥土。对模型进行网格划分,共得到33 846个单元、67 895个节点。
3) 边界条件设置。
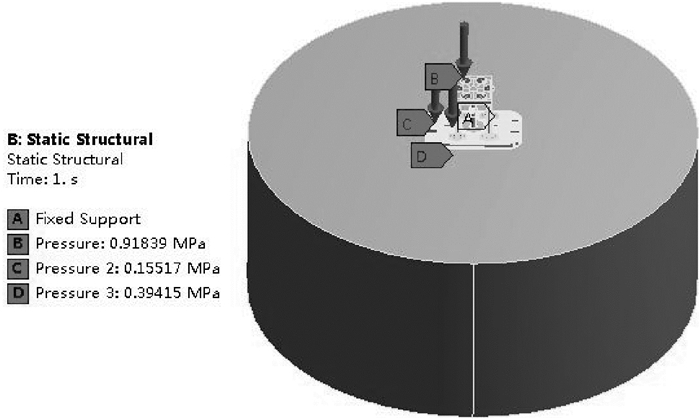
可控震源所能捕获的大地是有限的,在大地模型的边缘几乎没有位移,因此将大地模型的底面和圆柱面做6个自由度的约束(图 3中A)。可控震源工作时,首先将28 t自重的90%压在振动器顶板上、10%压在振动器平板上,重锤的重力也通过空气弹簧作用在平板上,然后振动器工作,因此载荷的设置为:90%的压重压在顶板的6个圆面上,每个圆面上的压力为0.918 39 MPa(图 3中A);10%的压重的分布在靠近平板左边缘的2个圆面和右边缘的2个圆面上,每个圆面上的压力为0.155 17 MPa(图 3中B);重锤的重力分布在靠近活塞杆的空气弹簧座上,每个空气弹簧座上的压力为0.394 15 MPa(图 3中C)。
|
| 图 3 振动器-大地有限元模型 Fig.3 Finite element model of vibrator-ground |
为了准确模拟可控震源的实际工作情况,利用ANSYS Workbench提供的集成平台,进行多模块联合仿真分析[19]。在ANSYS Workbench中首先调用Static Structural模块对振动器作静力学分析,然后将分析的结果作为初始条件转入Modal模块作预应力模态分析。
静力学分析中模型的变形结果如图 4所示。从图 4中可以看出,由于预应力的施加,振动器的顶板和立柱发生了细微的变形,其中顶板左右两侧中心处变形最大。在静力学分析的基础上,对模型进行预应力模态分析。根据线性系统机械振动理论,各阶固有振型的线性叠加即为结构表现出来的振动,其中低阶振型比高阶振型对结构的振动贡献大,基本决定了机械结构的振动特性[20],可控震源的额定工作频率为6~250 Hz,因此提取前6阶模态特性,分析结果如表 1所示。

|
| 图 4 施加预应力后的振动器变形情况 Fig.4 Deformation of vibrator with pre-stress |
| 阶次 | 频率/Hz | 振型描述 |
| 1 | 41.025 | 前后摆动 |
| 2 | 43.147 | 左右摆动 |
| 3 | 61.653 | 立柱及顶板以活塞杆为中心扭转 |
| 4 | 245.81 | 上下振动 |
| 5 | 266.22 | 平板与地表前后振动 |
| 6 | 266.29 | 平板与地表左右振动 |
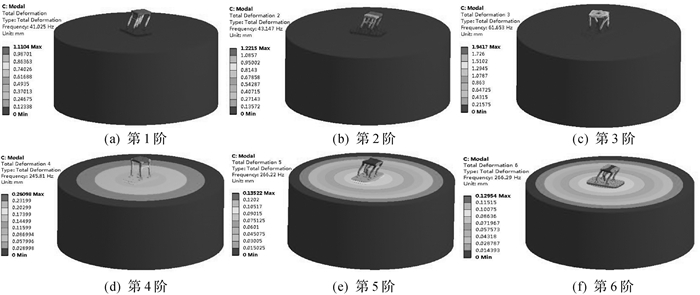
提取模型的前6阶振型,如图 5所示。从图 5中可以看出:振动器第1阶振型是振动器平板以上结构沿平板短轴方向(前后)摆动;第2阶振型是振动器平板以上结构沿平板长轴方向(左右)摆动;第3阶振型以扭转为主,即立柱及顶板以活塞杆为中心扭转;第4阶振型是以振动器及地表上下振动为主;第5阶振型是平板与地表前后振动;第6阶振型是振动器及地表左右摆动。实际工况下,为了保护伺服阀,可控震源的实际工作频率为6~125 Hz,振动器可能发生前3阶的共振。摆动和扭转是振动器的主要振动形式,这将引起振动器结构变形,导致可控震源输出信号畸变。
|
| 图 5 振动器的前6阶振型 Fig.5 The first six vibration modes of vibrator |
为了验证有限元模态计算结果的可靠性与准确性,在KZ-28型可控震源上通过现场试验对其进行验证。
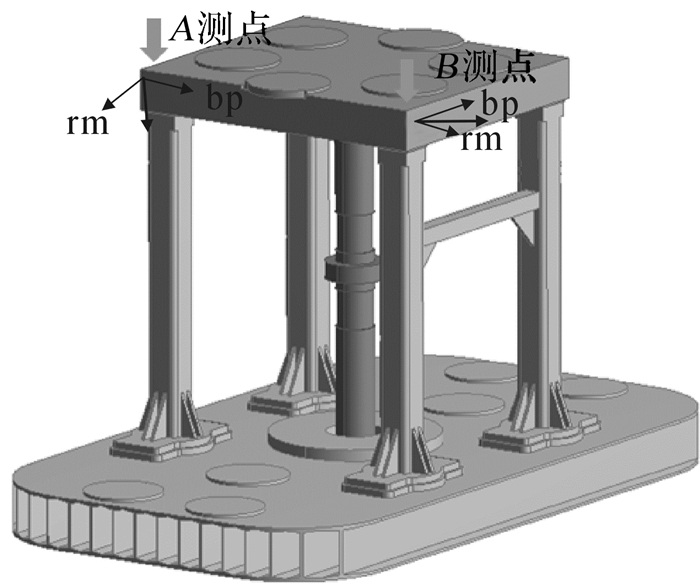
首先在振动器顶板上选择A, B两个测点,每个测点按正交方向(bp方向和rm方向)布置2个加速度传感器,如图 6所示;然后启动振动器作驱动幅度为80%的额定出力、扫描频宽为7~118 Hz的线性扫描,扫描时长为20 s,并利用NI PXI-4498型16通道采集卡采集振动器上的加速度信号。
|
| 图 6 振动器测点及加速度传感器布置情况 Fig.6 The arrangement of measuring points and acceleration sensors on vibrator |
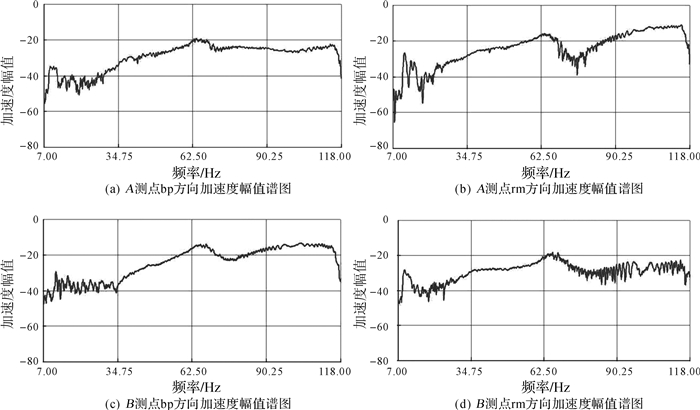
利用VCA自带的软件将采集的信号进行分析,得到A,B两个测点正交方向的加速度幅值谱图,如图 7所示。从图 7中可以看出4条曲线的起始段都出现了不规律的波动,这是由于振动器启动阶段的不稳定造成的。在图 7(a)和(d)中,A测点bp方向和B测点rm方向的加速度值在39 Hz左右都出现了稳定后的第1个峰值,可知振动器在39 Hz附近发生了共振,结合所测加速度的方向,判断其振型为前后摆动;同理,图 7(b)和(c)也表明,振动器在40 Hz附近发生了振型为左右摆动的共振。由图 7(a)、(b)、(c)、(d)可知,A,B两测点的加速度信号幅值曲线在65 Hz附近都存在凸起,表明该时间段振动器在bp和rm方向的加速度都出现了突变,说明振动器在频率为65 Hz附近发生了共振,再结合A,B两点在该时刻的合成加速度方向(图 8)可知,A测点和B测点的合成加速度方向呈扭转趋势,通过以上分析可以得知振动器在频率65 Hz左右发生了共振,振型为振动器扭转振动。
|
| 图 7 A测点与B测点加速度幅值谱图 Fig.7 Amplitude spectra of acceleration at measuring point A and B |

|
| 图 8 频率为65 Hz时A, B测点的合成加速度 Fig.8 The resultant accelerations of measuring point A and B with the frequency of 60 Hz |
试验的结果与有限元分析结论较为一致,表明振动器在39 Hz附近存在振型为前后摆动的共振,在40 Hz附近发生了振型为左右摆动的共振,并且在65 Hz时也发生了共振,相应的振型为扭转。但试验与有限元分析存在一定的误差,最大误差约为6.8%,推测主要的原因如下:首先,有限元模型中大地与振动器平板是理想接触,而试验中由于客观因素,二者之间的接触不可能为理想接触;其次,有限元模型进行了某些结构特征的简化,忽略了局部细节因素;最后,加速度传感器自身性能以及安装误差对试验结果的准确性也有影响。虽然试验并没有完全印证有限元分析的所有结果,但是从已测结果的相符程度来看,该有限元分析中的模型和方法是可靠的。共振引起振动器结构变形,导致可控震源输出信号畸变,降低油气勘探的准确度。因此,一方面,在设计振动器结构时应充分考虑振动器的这些变形,可以在相邻的2根立柱之间增加加强筋,从而加强立柱的刚度;另一方面,如果不是特殊要求,在作勘探设计时应尽量避免扫描频率与固有频率重叠,防止振动器共振,从而有效降低共振变形产生的源致干扰。
5 结论1) 建立了振动器-大地有限元模型,利用ANSYS Workbench软件对模型进行预应力模态分析,得到模型的前6阶固有频率和振型,分析了振动器的振动特性,表明振动器在实际工作频率范围内的共振为沿平板长轴和短轴的摆动以及以活塞杆为中心的扭转。
2) 试验表明振动器存在摆动和扭转,在设计振动器结构时需要考虑该振动及其产生的变形,提高振动器的刚度,特别是振动器立柱结构的刚度。
3) 模态分析的有限元仿真结果和试验结果基本一致,确认了振动器的振动特性,表明振动器共振会导致结构非激励性振动,这是导致振动器输出信号产生畸变的一个重要原因。在勘探时应尽量避免扫描频率与固有频率重叠, 防止振动器共振,从而有效降低共振变形产生的源致干扰。
| [1] |
佟训乾, 林君, 姜弢, 等.
陆地可控震源发展综述[J]. 地球物理学进展, 2012, 27(5): 1912–1921.
TONG Xun-qian, LIN Jun, JIANG Tao, et al. Summary of development of land vibrator[J]. Progress in Geophysics, 2012, 27(5): 1912–1921. DOI:10.6038/j.issn.1004-2903.2012.05.011 |
| [2] |
刘金中, 马铁荣.
可控震源的发展状况[J]. 石油科技论坛, 2008, 27(5): 38–42.
LIU Jin-zhong, MA Tie-rong. Development of the vibroseis[J]. Oil Forum, 2008, 27(5): 38–42. |
| [3] |
陶知非, 赵永林, 马磊.
低频地震勘探与低频可控震源[J]. 物探装备, 2011, 21(2): 71–76.
TAO Zhi-fei, ZHAO Yong-lin, MA Lei. Low frequency seismic and low frequency vibroseis[J]. Equipment for Geophysical Prospecting, 2011, 21(2): 71–76. |
| [4] |
刘洪斌, 陈如恒.
地震勘探震源的历史与发展[J]. 石油机械, 1997, 25(8): 43–45.
LIU Hong-bin, CHEN Ru-heng. Development of seismic source for geophysical exploration[J]. China Petroleum Machinery, 1997, 25(8): 43–45. |
| [5] |
徐爱军, 康丽生.
可控震源平板-大地振动模型及参数研究[J]. 中国煤田地质, 2001, 13(3): 62–64.
XU Ai-jun, KANG Li-sheng. Controllable seismic source plane-telluric vibration model and parameters[J]. Coal Geology of China, 2001, 13(3): 62–64. |
| [6] | WEI Zhou-hong. How good is the weighted-sum estimate of the vibrator ground force?[J]. The Leading Edge, 2009, 28(8): 960–965. DOI:10.1190/1.3192844 |
| [7] |
马磊, 赵永林, 王洪涛.
矩阵束方法在可控震源振动平板模态分析中的应用[J]. 物探装备, 2011, 21(5): 285–288.
MA Lei, ZHAO Yong-lin, WANG Hong-tao. Application of matrix pencil method for modal analysis on seismic vibrator[J]. Equipment for Geophysical Prospecting, 2011, 21(5): 285–288. |
| [8] | HENDRIX C M. Evaluation of high freuqency vibrator response[D]. Lawrence:University of Kansas, Department of Geology 2012:41-47. https://kuscholarworks.ku.edu/handle/1808/10663 |
| [9] | DEAN T, VEREER P L, LAYCOCK M, et al. The complexity of vibrator baseplate-ground interaction measured with a thin-film pressure pad and a downhole tool[C]//Eage Conference and Exhibition, Madrid, Jun.1-7, 2015. |
| [10] | WEI Z, PHILLIPS T F. Integrated analysis of the vibrator-ground system at high frequencies[J]. First Break, 2013, 31(1): 89–96. |
| [11] |
郝磊. 可控震源平板性能研究及改进[D]. 成都: 西南石油大学机电工程学院, 2014: 31-35.
HAO Lei. Research and improvement for vibroseis baseplate[D]. Chengdu:Southwest Petroleum University, School of Mechatronic Engineering, 2014:31-35. http://cdmd.cnki.com.cn/Article/CDMD-10615-1014415922.htm |
| [12] |
刘振武, 撒利明, 董世泰, 等.
中国石油物探技术现状及发展方向[J]. 石油勘探与开发, 2010, 37(1): 1–10.
LIU Zhen-wu, SA Li-ming, DONG Shi-tai, et al. Current situation and trend of geophysical technology in CNPC[J]. Petroleum Exploration & Development, 2010, 37(1): 1–10. |
| [13] |
王铁军, 郝会民, 李国旗, 等.
物探装备技术进展与发展方向[J]. 中国工程科学, 2010, 12(5): 78–83.
WANG Tie-jun, HAO Hui-min, LI Guo-qi, et al. Technical advance and development of China geophysical equipment[J]. Engineering Sciences, 2010, 12(5): 78–83. |
| [14] |
聂勇军, 廖启征.
桁架结构有限元及试验模态分析[J]. 机械设计与研究, 2011, 27(2): 61–64.
NIU Yong-jun, LIAO Qi-zheng. Finite element and experimental modal analysis of the truss[J]. Machine Design and Research, 2011, 27(2): 61–64. |
| [15] |
傅志方, 华宏星.
模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2002: 33-40.
FU Zhi-fang, HUA Hong-xing. Modal analysis theory and application[M]. Shanghai: Shanghai Jiaotong University Press, 2002: 33-40. |
| [16] |
袁启龙, 马娜, 周新涛, 等.
风力发电机叶片振动特性有限元分析[J]. 机械科学与技术, 2014, 33(5): 730–734.
YUAN Qi-long, MA Na, ZHOU Xin-tao, et al. Finite element analysis for vibration characteristics of wind turbine blade[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(5): 730–734. |
| [17] |
李云松, 任艳君, 程德蓉.
考虑预应力时风扇叶片模态特征分析[J]. 机械传动, 2010, 34(5): 49–51.
LI Yun-song, REN Yan-jun, CHENG De-rong. Modal analysis of fan blade of considering pre-stress[J]. Journal of Mechanical Transmission, 2010, 34(5): 49–51. |
| [18] | WEI Z, PHILLIP T F. Characterizing the vibrator captured ground mass system using finite element analyses[C]//SEG Technical Program Expanded Abstracts. Houston, Sep. 22-27, 2013. |
| [19] |
浦广益.
ANSYS Workbench 12基础教程与实例详解[M]. 北京: 中国水利水电出版社, 2010: 117-119.
PU Guang-yi. ANSYS Workbench 12 basic tutorials and example explanation[M]. Beijing: China Water-Power Press, 2010: 117-119. |
| [20] |
廖冰, 罗永峰.
基于振型贡献系数的空间结构振动反应研究[J]. 空间结构, 2014, 20(1): 9–16.
LIAO Bing, LUO Yong-feng. Vibration response computation of spatial structures based on mode contribution factors[J]. Spatial Structures, 2014, 20(1): 9–16. |



