对滑坡空间分布的研究, 目前尚处于定性研究阶段.近年来, 分形理论在各个领域的应用得到了飞速发展, 在滑坡空间分布的研究中也取得了一定的进展.分形理论在滑坡地质灾害研究领域中的应用研究主要集中于滑坡边界轨迹的几何分形结构[1]、滑坡边界轨迹的分形特征、滑坡多重分形特征[2-3]、滑坡分维预测研究[4]、滑坡预测分析[5]等方面.虽然滑坡的空间分布比较复杂, 但在一定尺度下具有一定的自相似性规律[6], 为此本文以江西省宁都县1: 5万地质灾害调查数据为基础, 基于变维分形理论, 用不同标尺下滑坡发育的程度来研究滑坡空间分布的分形特征.通过ArcGIS对宁都县1: 5万地质灾害调查的滑坡数据进行空间分布的分形研究, 定量地反映滑坡空间分布与地貌、岩土体、高程、坡度之间的敏感性关系.
1 变维分形1973年, 法国数学家B. B. Mandelbrot创建分形理论[7].其作为有序自然界的工具应用到社会中的各个方面, 它是介于一般数学和欧几里得几何秩序的混沌之间, 揭示和定量地刻画隐藏于复杂混乱现象背后的精细结构[1].在一般情况下, 若D为常数, 这种分形称为常维分形, 若D与特征线度r呈现函数关系, 则称之为变维分形, 表达式: D=F(r).
自然界中严格满足常维分形形式的现象是不存在的, 大量的复杂现象需要变维分形来描述[8].为了解决分维数D在双对数坐标下分形的非直线问题, 付昱华经过多年的研究提出变维分形的概念[9], 它将数据序列经过一系列1阶、2阶或者更多的阶数累计和变换, 建立各阶累计和的分段分维模型, 通过数据拟合, 选择拟合最好的作为其常维分形参数.经过变换它可以把任意函数关系式N=f(R)都转换为常分维形式N=Cr-D形式[10-11].
一般分形统计模型为: Y∝XF(D).式中X和Y是变量, F(D)表示分维数函数.可改写为: Y=CXF (D), 式中C为常数; F(D)表示分维数函数.
实际应用中, 分形统计数据在双对数坐标上拟合直线不理想情况下, 可以借助于变维分形的结果将数据进行一系列变换, 最后选出一种理想的变换, 使变换后的数据拟合成理想的直线, 变换后的数据能用常维分形理论来处理.将原始数据点(Ni, ri)(其中i取1到n的整数)经过变换, 绘制成双对数曲线.如果得到的曲线拟合为直线不理想, 就进行1阶、2阶……n阶累加变换, 直到得到的曲线拟合成很好的直线为止.具体如下.
将得出的序列{Ni}={N1, N2, …, Nn}进行依次累加, 可以得出一阶、二阶以至于n阶的累加和序列: {S1i}={N1, N1+N2, …, N1+N2+…+Nn}, {S2i}={S11, S11+S12, …, S11+S12+…+S1n}, …… …… …… ……, {Sni}={Sn-11, Sn-11+Sn-12, …, Sn-11+Sn-12+…+Sn-1n}
将各阶累积和的数据点标识在双对数坐标系上, 进行数据拟合, 找出拟合度最高的那组序列的数据点.于是就可以确定累积和阶次与常分维数.
M=N1/N2, N1=C1rF1(D), N2=C2rF2(D), M=CrF(D)
式中, M表示滑坡在某尺度下出现的比例; N1表示滑坡在某尺度下的面积; N2表示研究区中某尺度下的总面积.
2 宁都县滑坡空间分布的分形特征下面以宁都县滑坡空间分布与地形地貌、岩土体类型、高程、地形坡度的关系来说明这种分维关系.
2.1 滑坡空间分布与地形地貌之间分维分形特征通过ArcGIS的叠加功能, 对1: 5万调查得到的滑坡分布图与宁都县地貌图进行叠加处理, 得到各地貌滑坡分布面积.通过计算各坡度分布的比例, 按照比例从大到小排序, 用r表示, 依次取r=1, 2, 3, 4, 5, 代表不同的地貌类型(表 1).
|
|
表 1 滑坡分布面积与地貌分类之间的分段变维特征 Table 1 Sectioned variable dimension features of landslide distribution by landform types |
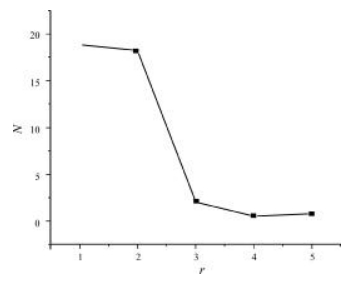
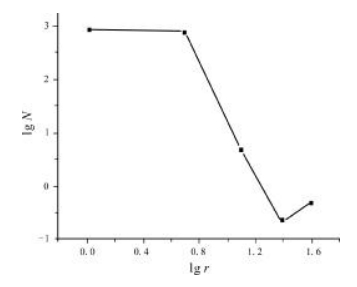
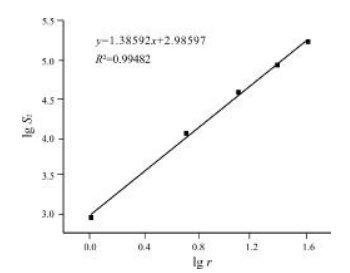
从图 1可以得出滑坡分布面积与地貌的关系没有相关性.从图 2可以看出, 在双对数坐标下, 滑坡分布面积与地貌关系呈散点状, 相关性差.对其进行一阶累计和分维变换后, 线性不明显(图 3).在进行二阶累积和分形变换后, 数据点呈理想的线性分布, 得出滑坡空间分布与地貌呈二阶累计和变维分形关系(图 4), 分维值1.38592, 相关系数0.99482.
|
图 1 滑坡分布面积与地貌关系图 Fig.1 Relation between landslide distribution and landform |
|
图 2 滑坡分布面积与地貌原始分维序列图 Fig.2 Original fractal dimension sequence diagram of landslide distribution and landform |

|
图 3 滑坡分布面积与地貌一阶累计和分段分维序列图 Fig.3 First-order cumulative total fractal distribution of landslide distribution and landform |
|
图 4 滑坡分布面积与地貌二阶累计和分段分维序列图 Fig.4 Second-order cumulative total fractal distribution of landslide distribution and landform |
通过ArcGIS的叠加功能, 对1: 5万调查得到的滑坡分布图与宁都县岩土体分类图进行叠加处理, 得到各岩土体滑坡分布面积(表 2).
|
|
表 2 滑坡分布面积与岩土体类型之间的分段变维特征 Table 2 Sectioned variable dimension features of landslide distribution by rock-soil mass types |
对数据进行一阶累积和变维分形变换, 所得数据点呈折线(图 5).对数据进行二阶累积和变维分形变换, 数据呈理想线性分布关系(图 6), 说明滑坡空间分布与岩土体类型呈二阶累计和变维分形关系, 分维值1.38592, 相关系数0.99428.

|
图 5 滑坡分布面积与岩土体一阶累计和分段分维序列图 Fig.5 First-order cumulative total fractal distribution of landslide distribution and rock-soil mass |

|
图 6 滑坡分布面积与岩土体二阶累计和分段分维序列图 Fig.6 Second-order cumulative total fractal distribution of landslide distribution and rock-soil mass |
利用DEM数据, 通过ArcGIS对其高程进行分段, 每50 m一段.通过ArcGIS的统计功能, 对1: 5万调查得到的滑坡数据与宁都县高程图进行统计分析, 得到各高程段滑坡分布面积, 见表 3.
|
|
表 3 滑坡分布面积与高程之间的分段变维特征 Table 3 Sectioned variable dimension features of landslide distribution by elevation |
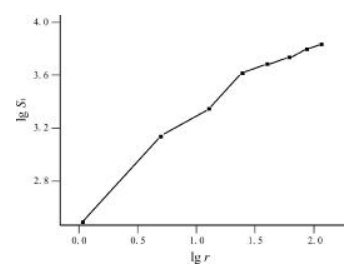
对数据进行一阶累计和分形变换, 结果呈折线(图 7).对数据进行二阶累计和分维变换, 可以看出二阶累积和与r在双对数坐标系中呈理想线性分布(图 8), 说明滑坡分布与高程呈二阶累计和变维分形.分维值1.51576, 相关系数0.99966.
|
图 7 滑坡分布面积与高程一阶累计和分段分维序列图 Fig.7 First-order cumulative total fractal distribution of landslide distribution and elevation |

|
图 8 滑坡分布面积与高程二阶累计和分段分维序列图 Fig.8 Second-order cumulative total fractal distribution of landslide distribution and elevation |
利用DEM数据得到宁都县坡度图.应用ArcGIS的空间分析功能, 对滑坡坡度进行分级; 应用ArcGIS的空间叠加功能, 对1: 5万地质灾害调查得到的滑坡数据与宁都县坡度图进行空间叠加统计分析处理, 得到各坡度区间滑坡分布面积(表 4).
|
|
表 4 滑坡分布面积与坡度之间的分段变维特征 Table 4 Sectioned variable dimension features of landslide distribution by slope |
通过对其进行一阶、二阶累积和变维分形变换(图 9、10), 可以看出滑坡空间分布与坡度呈二阶累积和变维分形关系, 分维值1.79319, 相关系数0.99769.

|
图 9 滑坡分布面积与坡度一阶累计和分段分维序列图 Fig.9 First-order cumulative total fractal distribution of landslide distribution and slope |

|
图 10 滑坡分布面积与坡度二阶累计和分段分维序列图 Fig.10 Second-order cumulative total fractal distribution of landslide distribution and slope |
通过宁都县滑坡空间分布研究, 揭示出滑坡与地形地貌、岩土体类型、高程、坡度成二阶累计和分形分布, 说明滑坡空间分布具有变维分形特征.
1) 分维值为常数, 可以从常维分形进一步研究滑坡特征.
2) 初步找到了滑坡空间分布与各影响因子之间的定量关系.可以通过变维分形之后得到的常分维数来定量地反映各影响因子与滑坡空间分布之间的关系.
3) 利用此次研究得出的定量的各影响因子与滑坡空间分布之间的敏感性关系, 可以在滑坡空间分布预测的时候, 更好地确定各影响因子的权重.从受人为较大影响的专家打分法过渡到量化的变化, 在以后的滑坡预测中可以从局部的滑坡资料, 得到量化的滑坡空间分布, 从而预测整个区域的滑坡分布.
4) 滑坡与地貌、岩土体类型、高程、坡度均呈二阶累计和分形分布, 在这4个分维值中, 地貌和岩土体类型分维值相同, 说明二者对滑坡分布的敏感度一致; 地貌、岩土体的分维值最小, 说明滑坡分布对地貌、岩土体的变化不敏感; 分维值最大的是坡度, 说明坡度的变化对滑坡发育影响最大, 滑坡对坡度敏感性大于地貌、岩土体、高程.
5) 在这4个分维值中, 地貌和岩土体类型分维值一致, 二者对滑坡分布敏感一致, 从另一个侧面说明, 我们研究滑坡的发育特征时切入点应该从微地貌单元、地层或工程地质岩组方面对滑坡空间分布方面研究.
6) 通过研究滑坡空间分布的变维分形特点, 使得滑坡空间分布研究从定向过渡到定量阶段.
| [1] |
邱海军.区域滑坡崩塌地质灾害特征分析及其易发性和危险性评价研究——以宁强县为例[D].西安: 西北大学, 2012.
|
| [2] |
张恋, 侯兴利. 基于分形理论的地质灾害空间分布特征研究[J]. 科技创新与应用, 2017(33): 189-190. |
| [3] |
张晨, 陈剑平, 王清, 等. 基于分形理论和流域水系分布特征的泥石流研究[J]. 水利学报, 2011, 42(3): 351-356. |
| [4] |
文洪, 杨梅忠, 杜江丽. 基于分形理论的滑坡空间分布分维值意义探讨[J]. 中国科技信息, 2013(1): 47-48. DOI:10.3969/j.issn.1001-8972.2013.01.010 |
| [5] |
郑新民, 王兰生. 分形理论在区域地质灾害预测中的应用[J]. 地质灾害与环境保护, 1998, 9(3): 1-4. |
| [6] |
王忠志.基于GIS的重庆市地质灾害空间分布的分形分维研究[D].重庆: 西南大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10635-1014259168.htm
|
| [7] |
张彦, 林德宏. 系统自组织概论[M]. 南京: 南京大学出版社, 1990: 76-87.
|
| [8] |
薛天放, 杨庆, 栾茂田. 基于GIS技术的滑坡空间分布的分形特征研究[J]. 岩土力学, 2007, 28(2): 347-351, 354. DOI:10.3969/j.issn.1000-7598.2007.02.027 |
| [9] |
付昱华. 风浪流参数的分形分析[J]. 港工技术, 1996(3): 6-9. |
| [10] |
付昱华. 变换形成的分形与海洋环境数据分析预测[J]. 海洋通报, 2000, 19(1): 79-88. DOI:10.3969/j.issn.1001-6392.2000.01.011 |
| [11] |
侯威, 张茜, 楼蓉蓉, 等. 基于变维分形理论的滑坡空间分布特征研究[J]. 安全与环境工程, 2012, 19(4): 17-21. DOI:10.3969/j.issn.1671-1556.2012.04.004 |
 2019, Vol. 28
2019, Vol. 28

