2 浙江金华山亚热带森林生态系统野外科学观测研究站, 浙江 金华 321004)
森林在维持全球碳平衡和缓解气候变化中发挥着重要作用[1~2],准确估算森林生态系统碳储量和固存率越来越引起人们的广泛关注[3~4],尤其是在应对全球气候变化的大背景下[5~6]。森林碳储量变化受森林生物量及其动态的影响[7],而森林生物量的估算方法在某种程度上决定着其估算精度[3, 8~9]。因此,建立更加精确的森林生物量模型对估算森林碳储量、监测森林资源动态及提高森林管理至关重要。
森林生物量研究方法主要包括实测法、模型法和遥感法[10]。实测法虽准确但费时费力,实施困难,且对森林具有破坏性,因此仅适用于小尺度局域研究[11];遥感法基于遥感技术估算获得森林生物量,可用于大尺度区域的估算,但仍需结合野外样地调查和生物量方程进行验证[12]。基于生物量相对生长方程的模型法不仅可用于局地和单树种的生物量估算,也可拓展到大尺度和多树种,是准确估算植被生物量的主要方法之一[13];经过长期努力,该方法获得很大进展[14~16],但目前仍存在较多问题,尤其是通用型、普适性生物量相对生长方程的缺乏,限制了我们快速、精确估算区域和全球森林生物量的能力。
近年来,研究人员在积极探索适用于区域、国家乃至全球尺度的立木生物量估算模型[13~14, 17~23]。由于起源、生境差异等因素的影响,即使同一物种在不同地区的生物量也表现出一定差异[24~27]。因此,大尺度生物量建模需要在方法上进行改进,比如,将气候、环境指标等影响因素纳入到生物量建模中[7, 28~32],或引入机器学习的方法,以提高大尺度生物量模型估算精度[15, 33~35]。然而,现有建模方法大多基于研究者认为的某一种最适用方法开展研究,缺乏多方法的横向比较。
根据文献统计,我国已建立5900多个生物量方程(包括各器官分量和总量),涉及200多个树种[16]。但这些已建立的方程多数是针对独立研究地点或特定小区域的植被进行研究,受限于研究对象及研究尺度,难以推广到大尺度森林生物量估算中[14]。因此,部分学者尝试建立适用于我国的大尺度立木生物量模型[3, 7, 15, 28~29, 36~41]。但大多以针叶树种为主,缺乏适用于常见阔叶树种以及全国不同森林类型优势种的大尺度立木生物量模型[29];而且,大多基于单一树种构建方程,缺乏适用于多树种的普适性生物量模型。
因此,本研究通过广泛搜集已正式发表的文献数据,基于植物系统发育关系和植物木材密度相似性[14, 42],针对我国一些常见树种及其树种类型组合,结合基本模型、LSSVM模型和哑变量模型3种生物量建模方法,建立适用于我国不同树种类型的大尺度生物量方程组,讨论所选树种在其分布范围内建立普适性方程(组)的可行性。对研建的生物量模型进行综合评价,判断不同方法在大尺度生物量建模上的优缺点,为建立大尺度生物量模型提供参考,为提高我国森林生物量评估精度提供科学支撑。
1 材料和方法 1.1 文献搜集利用中国国家数字图书馆、中国林业数字图书馆、中国知网(CNKI)、维普网、万方数据知识服务平台、Web of Science等国内外重要数据库,以关键词“森林生物量”、“碳储量”、“生物量方程”和“生物量模型”等检索,搜集我国(未包括中国香港、澳门和台湾地区)生物量相关文献,并结合已发表的我国生物量数据库文献[16, 36, 43~45]进行数据补充和筛选。共计获得1536篇论文/书籍内的6136条标准木数据和5090条生物量方程数据,涉及研究对象和研究目的各不相同,为保证数据的可靠性和准确性,以如下标准筛选文献: 1)研究对象为人为干扰较少、植被生长状况稳定的林分。不包括荒漠、农林复合系统、萌生林及湿地等林分;2)收集文献仅限于使用或符合我国林业行业标准[46~47]得到的生物量相关数据;3)对文献内数据或生物量方程估算数据偏差较大的,即不符合林木生长规律或显著偏离树种生物量均值的数据,根据林学及植物学相关知识来决定其取舍。部分文献中少量植物组织的生物量数据缺测,文献中有生物量方程的则利用该方程计算补充缺失数据,无生物量方程者则利用就近的相同或相似生境中同一树种的其他文献数据进行补全。
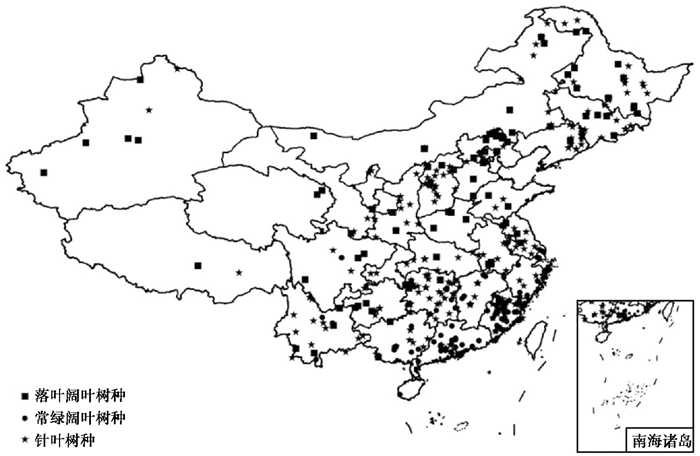
筛选了1982~2019年间发表的287篇文献,包括864条生物量实测数据以及2024条生物量方程数据。涉及31个落叶阔叶树种、27个常绿阔叶树种以及5个针叶树种,共7个科63个树种(表 1);共涉及到461个研究点,其地理分布如图 1。收集到的信息包括研究区域(省、市、研究地点)、经纬度(°)、海拔(m)、年均温(℃)和年降水(mm)等地理与生境因子,林分起源、林龄(a)、胸径(cm)、树高(m)等测树因子,以及干、枝、叶、根生物量(kg)和对应的生物量方程(各分量方程及总量方程)及其决定系数(R2)等数据指标。
| 表 1 我国生物量研究的主要树种 Table 1 Major tree species for biomass research in China |
|
图 1 我国主要树种生物量方程的研究点分布 Fig. 1 Distribution of study sites for biomass equations of major tree species in China |
众多研究表明,数据、方法等的差异会导致大尺度森林生物量估算的潜在误差[48],但不同方法间的差异却无法准确量化。为此,我们选择了落叶阔叶、常绿阔叶和针叶这3种不同树种类型(表 1),并结合叶型、叶候和木材比重相似性等筛选相近或相似树种,对这3种树种类型分别建立3种不同方法的大尺度生物量估算模型,并评估其优劣。
1.2.1 基本模型生物量方程通常以异速生长理论为基础[13, 49],建立生物量与易于测量的测树因子之间的相对生长关系方程[50],通常表述为[29, 51]:
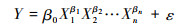
|
(1) |
公式(1)中,Y为立木生物量,Xn为反映立木大小的指标,βn为模型参数,ε为模型误差。而实际运用中,通常简化为以胸径(D)、树高(H)、D2 H等测树因子为自变量的幂函数形式[52~53],即:
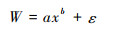
|
公式(2)中,W为立木生物量,x为测树因子,a、b为模型参数。
1.2.2 LSSVM模型最小二乘支持向量机(Least Square Support Vector Machine,简称LSSVM)是一种遵循结构风险最小化原则的机器学习方法[54~55]。以最小二乘法线性方程组代替了支持向量机(Support Vector Machine,简称SVM)的二次规划问题,降低SVM的计算复杂性,提高求解速度[54~55]。使用等式约束替换不等式约束,通过解决等式约束以及最小二乘问题,使得计算得到进一步简化[54]。
基于LSSVM的生物量建模主要是在SVM框架下,将原有数据集结合不同核函数,对生物量基本模型参数进行优化,通过引入拉格朗日函数,借助微分求导,得到生物量模型的优化函数[56]。LSSVM模型的目标函数可表述为:
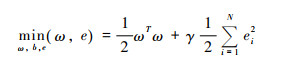
|
(3) |
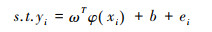
|
(4) |
其中,ei为误差变量,γ为正则项参数,控制对误差项的惩罚程度,ω和b为待定参数,ω为ωT的权向量,T表示矩阵转置,N为样本数量,xi和yi分别为样本自变量和因变量,s.t.表示约束条件,φ(xi)为投影到高维空间的样本。
LSSVM的预测函数可表述为:
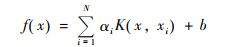
|
(5) |
本文选定的核函数为径向基核函数:
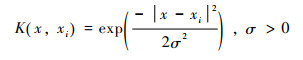
|
(6) |
其中,K(x,xi)为选定的核函数,xi为支持向量,α为拉格朗日乘子,σ为自由参数。
由于LSSVM模型的参数设定和优化是影响模型结果的重要因素,因此本文具体计算过程、方法介绍以及代码参考了相关专业文献[15, 54~55],并根据本文数据情况进行了一定修改。
1.2.3 哑变量模型立木生物量除受胸径、树高等测树因子影响外,起源、生境、气候等其他因素也对大尺度生物量建模具有影响[28, 57~59]。由此,我们选择森林起源和生长区域这两个易于获取的指标进行哑变量生物量建模。
森林起源分为天然和人工2个类型。生长区域因涉及范围较广,且样本单元数差异较大,综合考虑立木生境条件差异和建模数据的平衡,分为3个区域: 南部地区r1(苏、浙、沪、皖、闽、赣、鄂、湘、川、渝、滇、黔、粤、桂、琼)、中部地区r2(京、津、晋、冀、鲁、豫、甘、陕、新、青)和北部地区r3(黑、吉、辽、宁、蒙以及冀、新、甘的部分区域)。由于我国常绿阔叶树种多分布于南方地区,再对常绿阔叶树种分布区划分为东部地区sr1(苏、浙、沪、赣、皖)、华南地区sr2(粤、桂、闽、琼)和西南地区sr3(川、渝、滇、黔、湘、鄂、藏)这3个亚区域。
因此,公式(2)对应的哑变量立木生物量模型基本形式为:
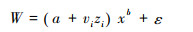
|
(7) |
公式(7)中,zi为哑变量,vi为相对应的随机效应参数,其他符号同公式(2)。由于各个树种组涉及了2种不同起源和3个生长区域,哑变量应包括以下4种情况:
(1) 只考虑森林起源影响,则仅包含1个哑变量z1:
即天然林z1=1,人工林z1=-1。
(2) 考虑分布区域的影响时(常绿阔叶树种的3个亚区域同理),则包括2个哑变量z2和z3:
区域r1或sr1时,取z2=1,z3=0;区域r2或sr2时,取z2=0,z3=1;区域r3或sr3时,取z2=-1,z3=-1。
(3) 考虑区域和起源独立影响时,则包含z1、z2、z3共3个哑变量,取值方式同上。
(4) 考虑区域和起源的交互影响时,则包括z1、z2、z3、z4、z5这5个哑变量:
区域r1或sr1、天然林,取z1=1,z2=0,z3=0,z4=0,z5=0;
区域r1或sr1、人工林,取z1=0,z2=1,z3=0,z4=0,z5=0;
区域r2或sr2、天然林,取z1=0,z2=0,z3=1,z4=0,z5=0;
区域r2或sr2、人工林,取z1=0,z2=0,z3=0,z4=1,z5=0;
区域r3或sr3、天然林,取z1=0,z2=0,z3=0,z4=0,z5=1;
区域r3或sr3、人工林,取z1=-1,z2=-1,z3=-1,z4=-1,z5=-1。
因此,需对以上不同林分起源、生长区域及其之间的独立影响、交互影响这4种情况分别进行模拟,探究2种因素对大尺度生物量建模的影响[26, 29, 60]。
以上述3种不同方法分别建立生物量模型并进行比较,可探究不同方法在大尺度生物量建模上的异同点。同时,3种方法均在基本模型的基础上结合不同算法构建生物量方程,由此可在不加大模型复杂程度的前提下提升模型的评估效果。
1.3 模型评价为综合评价模型的预估效果,本文选用决定系数(R2)、标准差(SEE)、总相对误差(TRE)和预估精度(P)等指标作为检验标准[60~61],
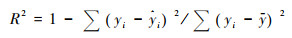
|
(8) |
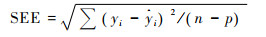
|
(9) |
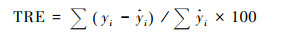
|
(10) |
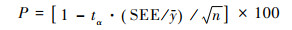
|
(11) |
公式(8)~(11)中,yi为生物量实测值,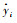
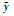
从模型的参数估计值及模型评价指标(表 2)可以看出,对于地上生物量来说,使用D2 H变量优于D变量模型,增加树高变量可以提升模型模拟效果;而地下生物量则相反,主要取决于胸径,与树高关系相对不显著。
| 表 2 基本模型参数估计值及模型评价指标* Table 2 Basic model parameter estimates and model evaluation indicators |
从检验结果(表 2)来看,不同树种类型的地上生物量模型决定系数(R2)大多在0.85以上(落叶阔叶树种0.80),针叶树种甚至在0.90以上,预估精度(P)在95 % 以上,但是模拟的总相对误差(TRE)相对较高,超出了±5 % 的范围,对于地上生物量可能存在一定误差;地下生物量的R2大多在0.75以上,P在90 % 以上,TRE同样超出了±5 % 的范围。因此,我们认为基本模型在大尺度生物量建模上受限于自变量,忽略了非测树因子对植物生物量的影响,可能导致模型评估的误差较大。
2.2 LSSVM模型从LSSVM方法建模的参数估计值及模型评价指标(表 3)来看,相对于基本模型,除落叶阔叶树种单变量模型外,LSSVM模型在R2、TRE、P上均有所提升。LSSVM模型TRE大多在±5 % 以内,误差相对较小,能很好地估算生物量。说明LSSVM虽同样未考虑到非测树因子对生物量的影响,其通过机器学习的方式,将原有求解过程转换为求解线性方程组,得到基于基本模型的优化变量,降低了模型模拟的相对误差。因此,使用LSSVM方法进行大尺度生物量建模总体是可行的,在基本模型的基础上,很好地降低模型相对误差,提升模型模拟精度。
| 表 3 LSSVM模型及模型评价指标 Table 3 LSSVM model parameter estimates and model evaluation indicators |
针对哑变量模型构建的不同森林起源、分布区域及其之间的独立影响、交互影响这4种情况所选用的模型参数(表 4)及全部的检验结果(表 5),可分别获得针对不同来源(模型参数v1)和不同区域(模型参数v2、v3)的完整模型的回归曲线(图 2和3)。
| 表 4 哑变量模型参数值 Table 4 Parameters of dummy variable model |
| 表 5 哑变量模型评估结果 Table 5 Evalution of dummy variable model |
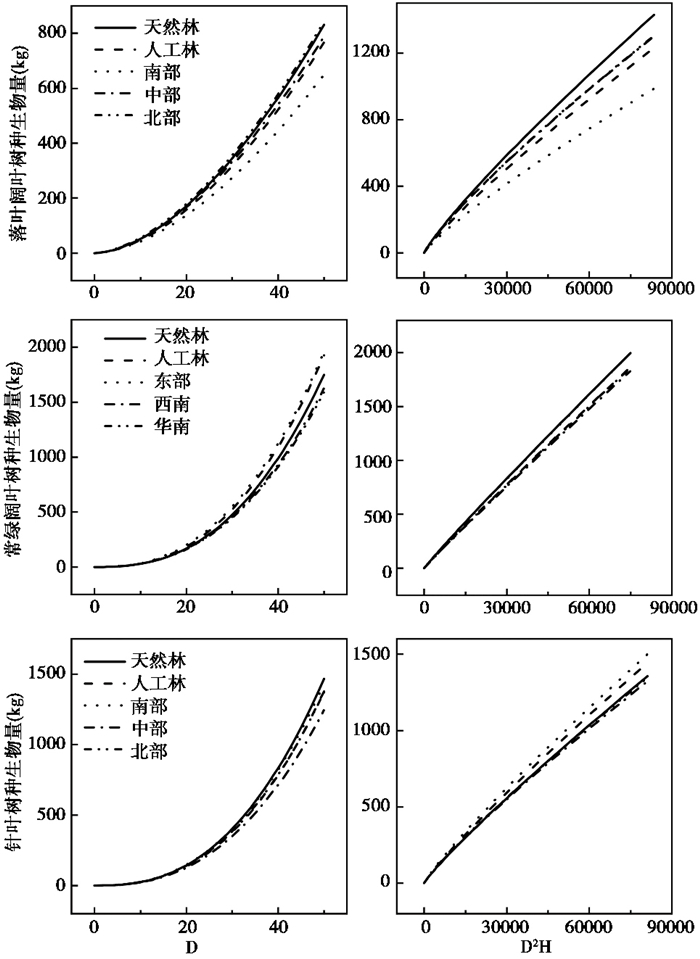
|
图 2 不同起源与区域的哑变量模型地上生物量回归曲线 Fig. 2 Above-ground biomass regression curves for dummy variable models on the basis of different forest sources and regions |
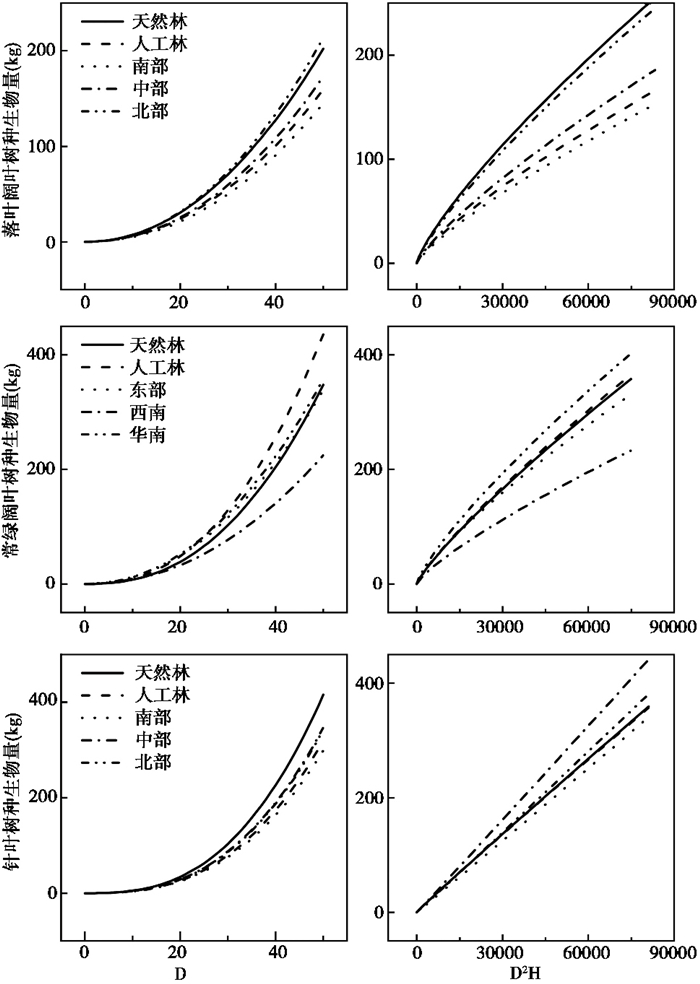
|
图 3 不同起源和区域的哑变量模型地下生物量回归曲线 Fig. 3 Below-ground biomass regression curves for dummy variable models on the basis of different forest sources and regions |
由模型参数值可以看出,同一树种类型地上/地下哑变量模型通用参数a、b相差不大,但随机参数vi则存在一定差异,表明森林起源和生长区域对树种的模拟结果存在一定影响。从图 2和3来看,森林起源不同时,落叶阔叶树种和针叶树种天然林生物量大于人工林,常绿阔叶树种则相反。对于不同区域的模拟,落叶阔叶树种生物量由南向北表现出递增的趋势,针叶树种地上生物量南方较高,地下生物量则相反;常绿阔叶树种生物量为沿海区域(华南、东部)大于内陆地区(西南)。
从哑变量模型评估结果(表 5)来看,单变量地上生物量模型R2在0.8以上,双变量模型R2在0.9以上,模型TRE在大多在±5 % 以内,P均在93 % 以上,针叶树种甚至在95 % 以上,模拟效果相对较好。从模拟结果来看,落叶阔叶树的森林起源、分布区域及其之间的独立影响和交互影响这4种哑变量模型的模拟结果差异不显著,分布区域和森林起源的差异对落叶阔叶树影响较低,可能更多的受树种差异的影响;而常绿树种则明显受分布的亚区域影响较大;而分布区域和森林起源对针叶树生物量均有较大影响。
3 讨论建立普适性或区域性的森林生物量相对生长方程,一直是林学界和生态学界努力的方向[3, 14~15, 63~65]。多种模型联合及新统计模型的应用,为该工作增添了活力。本研究结合基本模型、LSSVM模型和哑变量模型3种不同的生物量建模方法,构建了适用于我国落叶阔叶树种、常绿阔叶树种和针叶树种3种主要树种类型的大尺度生物量相对生长方程模型。通过对比发现,哑变量模型和LSSVM模型的R2、SEE、TRE和P优于基本模型,并且多数情况下以哑变量模型最优。因此,我们认为在构建大尺度生物量方程时,基本模型具有一定局限性。由于生境、起源等因素的影响,即使同一树种的生物量在同一或不同区域也存在差异[14, 24~25, 29],而基本模型受变量限制,忽略了大尺度上不同地区、不同树种的生物量差异,仅考虑到数据的回归关系,导致方程存在一定不确定性,进行生物量评估时可能产生较大误差[66]。LSSVM建模方法则在基本模型的基础上,基于机器学习原理[67]将求解问题转换为求解线性矩阵方程,避免了建模参数的局部寻优[15],一定程度上降低基本模型的不确定性。哑变量模型同样以基本模型为基础,引入了森林起源、分布区域等分类哑变量,建立哑变量方程组,对不同森林起源和分布区域的树种进行分类模拟、建模,即哑变量模型通过引入环境变量,更加全面的反映出影响生物量差异的因素,降低了非测树因子等因素对生物量的影响,通过降低各模型组内误差的方式,提升模型模拟效果。但通过验证发现,3种不同模型在局部适用性上都存在一定差异,在整体模拟上却差异不显著。因此,在评估大尺度森林生物量时,基本模型可以达到快速估算要求,但存在较大不确定性;LSSVM建模方法和哑变量模型能够通过机器学习或分类的方式得到优化模型,减少大尺度生物量评估的不确定性,提升大尺度生物量模拟精度。
过去研究多集中在单一模型和单一或少数树种的生物量方程建模[15~16],本文聚焦于多模型联合应用以及对主要树种类型的建模,在多模型比较和普适性方面有所提高。本文虽然以生物量方程数据为主进行研究,在一定程度上损失了数据的原始特征值[14],但所构建的生物量模型估算各个主要树种类型的地上生物量和地下生物量的模拟精度均分别在95 % 和90 % 以上,模拟效果仍然较好。相较于先前单一树种的大尺度生物量模型[7, 29, 36, 68],我们研建的主要树种类型模型在不降低模型效果前提下可适用于更多树种;并且不局限于单一方法建模[15, 29, 36],明确了不同建模方法在我国大尺度生物量评估中的优缺点。
从落叶阔叶树种、常绿阔叶树种和针叶树种3种主要树种类型的模拟结果来看,落叶阔叶树种受林分起源和分布区域的影响影响较大,不同森林起源和分布区域将生物量差异较大,表现出由南向北递增的趋势,增加变量能显著提升其模拟效果,这也验证了前人的结论[39, 62, 69~71]。针叶树种则相反,受森林起源和分布区域影响较小,增加变量并未提升其模拟效果。但不同针叶树种(本研究仅以松科植物为代表)大多集中分布于相似的区域,故不同松科植物的种间生物量差异较大,通过不同区位哑变量模型的模拟结果进一步证实这一差异,并且可能由于种间差异的影响,导致不同森林起源的哑变量模型表现出前人结论相反的结果[7, 26],但具体影响因素有待进一步验证。而可能是由于沿海区域水热条件较好所致[29],常绿阔叶树种受分布区域影响较大,表现出沿海区域植物的生物量大于内陆的现象。因此,根据树种类型等宽幅植物分类方法,对相同或相似树种建立适用于大尺度的多树种普适性生物量模型,可以达到准确、快速评估森林生物量的要求[14, 52, 72],对植被组成复杂区域的森林生物量快速评估具有重要意义。
4 结论通过基本模型、LSSVM模型和哑变量模型3种方程,结合D、D2H两个生物量估算最常用的自变量[15],研建了落叶阔叶树种、常绿阔叶树种和针叶树种3种树种类型的不同生物量方程发现,本文构建的大尺度通用生物量模型检验结果较好,可应用于我国大尺度生物量估算之中,并且我们认为构建相同或相似树种的通用型生物量方程可达到较高的估算精度。3种建模方法对比发现,在大尺度生物量估算时,对于精度相对较低且要求快速估算的可以选择以基本模型进行方程研究,并且可根据生物量的差异选择是否需要增加树高变量;对于生物量、生境等指标影响较大时可选择增加自变量、引入分类因子的哑变量模型,而树种生物量差异较小、数据获取困难时可采用LSSVM模型等,不同方法在模型整体上并不存在显著性差异,仅在单株模拟精度上可能存在较大不确定性。不同自变量对比发现,地上生物量D2H变量模型优于D变量模型,而地下生物量则相反,在缺少树高数据或不能准确测定树高时,仅使用胸径作为自变量构建方程也能达到相对较高的预估精度。综上所述,大尺度生物量建模引用LSSVM或哑变量模型等方法,对提升生物量评估精度具有重要意义,将不同学科建模方法融合到生物量评估中,也是未来大尺度生物量评估的发展方向。
致谢: 感谢审稿专家和编辑部老师建设性的修改意见!
| [1] |
Pan Y D, Birdsey R A, Fang J Y, et al. A large and persistent carbon sink in the world's forests[J]. Science, 2011, 333(6045): 988-993. DOI:10.1126/science.1201609 |
| [2] |
Tomppo E, Gschwantner T, Lawrence M, et al. National Forest Inventories: Pathways for Common Reporting[M]. Netherlands: Springer, 2010: 3-7.
|
| [3] |
Fang J Y, Chen A P, Peng C H, et al. Changes in forest biomass carbon storage in China between 1949 and 1998[J]. Science, 2001, 292(5525): 2320-2322. DOI:10.1126/science.1058629 |
| [4] |
Woodbury P B, Smith J E, Heath L S. Carbon sequestration in the U. S.forest sector from 1990 to 2010[J]. Forest Ecology and Management, 2007, 241(1-3): 14-27. DOI:10.1016/j.foreco.2006.12.008 |
| [5] |
郑景云, 刘洋, 郝志新, 等. 过去2000年气候变化的全球集成研究进展与展望[J]. 第四纪研究, 2021, 41(2): 309-322. Zheng Jingyun, Liu Yang, Hao Zhixin, et al. State-of-art and perspective on global synthesis studies of climate change for the past 2000 years[J]. Quaternary Sciences, 2021, 41(2): 309-322. |
| [6] |
徐建, 刘珺, 陈漪馨, 等. 浅述低纬过程在全球气候变化中的重要性[J]. 第四纪研究, 2020, 40(3): 595-604. Xu Jian, Liu Jun, Chen Yixin, et al. Brief notes on significance of low-latitude processes in global climate change[J]. Quaternary Sciences, 2020, 40(3): 595-604. |
| [7] |
Zeng W S, Fu L Y, Xu M, et al. Developing individual tree-based models for estimating aboveground biomass of five key coniferous species in China[J]. Journal of Forestry Research, 2018, 29(5): 1251-1261. DOI:10.1007/s11676-017-0538-9 |
| [8] |
于贵瑞, 方华军, 伏玉玲, 等. 区域尺度陆地生态系统碳收支及其循环过程研究进展[J]. 生态学报, 2011, 31(19): 5449-5459. Yu Guirui, Fang Huajun, Fu Yuling, et al. Research on carbon budget and carbon cycle of terrestrial ecosystems in regional scale: A review[J]. Acta Ecologica Sinica, 2011, 31(19): 5449-5459. |
| [9] |
雷相东, 张会儒, 牟惠生. 东北过伐林区蒙古栎林分相容性生物量模型研究[J]. 第四纪研究, 2010, 30(3): 559-565. Lei Xiangdong, Zhang Huiru, Mu Huisheng. Compatible stand biomass models of Mongolia oak forests in over logged forest regions Northeast China[J]. Quaternary Sciences, 2010, 30(3): 559-565. DOI:10.3969/j.issn.1001-7410.2010.03.14 |
| [10] |
张鹏, 冯兆东, 王俊人. 森林生物量研究方法综述[J]. 能源与节能, 2014(6): 102-104. Zhang Peng, Feng Zhaodong, Wang Junren. On the research methods of forest biomass[J]. Energy and Energy Conservation, 2014(6): 102-104. DOI:10.3969/j.issn.2095-0802.2014.06.044 |
| [11] |
Satoo T, Madgwick H A. Forest Biomass[M]. Netherlands: Springer, 1982: 2-4.
|
| [12] |
Clark D B, Kellner J R. Tropical forest biomass estimation and the fallacy of misplaced concreteness[J]. Journal of Vegetation Science, 2012, 23(6): 1191-1196. DOI:10.1111/j.1654-1103.2012.01471.x |
| [13] |
Návar J. Allometric equations for tree species and carbon stocks for forests of Northwestern Mexico[J]. Forest Ecology and Management, 2009, 257(2): 427-434. DOI:10.1016/j.foreco.2008.09.028 |
| [14] |
Jenkins J C, Chojnacky D C, Heath L S, et al. National-scale biomass estimators for United States tree species[J]. Forest Science, 2003, 49(1): 12-35. |
| [15] |
周国逸, 尹光彩, 唐旭利, 等. 中国森林生态系统碳储量: 生物量方程[M]. 北京: 科学出版社, 2018: 2-80. Zhou Guoyi, Yin Guangcai, Tang Xuli, et al. Carbon Stocks in Chinese Forest Ecosystems: The Biomass Equation[M]. Beijing: Science Press, 2018: 2-80. |
| [16] |
Luo Y J, Wang X K, Ouyang Z Y, et al. A review of biomass equations for China's tree species[J]. Earth System Science Data, 2020, 12(1): 21-40. DOI:10.5194/essd-12-21-2020 |
| [17] |
Bi H Q, Turner J, Lambert M J. Additive biomass equations for native eucalypt forest trees of temperate Australia[J]. Trees, 2004, 18(4): 467-479. |
| [18] |
Zianis D, Muukkonen P, Mäkipää R, et al. Biomass and Stem Volume Equations for Tree Species in Europe[M]. Finland: Silva Fennica, 2005: 7-63.
|
| [19] |
Snorrason A, Einarsson S F. Single-tree biomass and stem volume functions for eleven tree species used in Icelandic forestry[J]. Icelandic Agricultural Sciences, 2006, 19: 15-24. |
| [20] |
Muukkonen P. Generalized allometric volume and biomass equations for some tree species in Europe[J]. European Journal of Forest Research, 2007, 126(2): 157-166. DOI:10.1007/s10342-007-0168-4 |
| [21] |
Blujdea V, Pilli R, Dutca I, et al. Allometric biomass equations for young broadleaved trees in plantations in Romania[J]. Forest Ecology and Management, 2012, 264: 172-184. DOI:10.1016/j.foreco.2011.09.042 |
| [22] |
Fayolle A, Doucet J-L, Gillet J-F, et al. Tree allometry in Central Africa: Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks[J]. Forest Ecology and Management, 2013, 305: 29-37. DOI:10.1016/j.foreco.2013.05.036 |
| [23] |
Bi H Q, Murphy S, Volkova L, et al. Additive biomass equations based on complete weighing of sample trees for open eucalypt forest species in south-eastern Australia[J]. Forest Ecology and Management, 2015, 349: 106-121. DOI:10.1016/j.foreco.2015.03.007 |
| [24] |
Forrester D I, Tachauer I H H, Annighoefer P, et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate[J]. Forest Ecology and Management, 2017, 396: 160-175. DOI:10.1016/j.foreco.2017.04.011 |
| [25] |
Stegen J C, Swenson N G, Enquist B J, et al. Variation in above-ground forest biomass across broad climatic gradients[J]. Global Ecology and Biogeography, 2011, 20(5): 744-754. DOI:10.1111/j.1466-8238.2010.00645.x |
| [26] |
Zeng W S. Using nonlinear mixed model and dummy variable model approaches to develop origin-based individual tree biomass equations[J]. Trees, 2015, 29(1): 275-283. DOI:10.1007/s00468-014-1112-0 |
| [27] |
Zeng W S, Zhang L J, Chen X Y, et al. Construction of compatible and additive individual-tree biomass models for Pinus tabulaeformis in China[J]. Canadian Journal of Forest Research, 2017, 47(4): 467-475. DOI:10.1139/cjfr-2016-0342 |
| [28] |
Fu L Y, Zeng W S, Zhang H R, et al. Generic linear mixed-effects individual-tree biomass models for Pinus massoniana in Southern China[J]. Southern Forests, 2014, 76(1): 47-56. DOI:10.2989/20702620.2013.870389 |
| [29] |
Zeng W S, Zhang H R, Tang S Z. Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales—A case study for masson pine(Pinus massoniana)in Southern China[J]. Canadian Journal of Forest Research, 2011, 41(7): 1547-1554. DOI:10.1139/x11-068 |
| [30] |
Zang H, Lei X D, Zeng W S. Height-diameter equations for larch plantations in northern and northeastern China: A comparison of the mixed-effects, quantile regression and generalized additive models[J]. Forestry, 2016, 89(4): 434-445. DOI:10.1093/forestry/cpw022 |
| [31] |
Zou W T, Zeng W S, Zhang L J, et al. Modeling crown biomass for four pine species in China[J]. Forests, 2015, 6(2): 433-449. |
| [32] |
傅煜, 雷渊才, 曾伟生. 单木生物量模型估计区域尺度生物量的不确定性[J]. 生态学报, 2015, 35(23): 7738-7747. Fu Yu, Lei Yuancai, Zeng Weisheng. Uncertainty analysis for regional-level above-ground biomass estimates based on individual tree biomass model[J]. Acta Ecologica Sinica, 2015, 35(23): 7738-7747. |
| [33] |
雷相东. 机器学习算法在森林生长收获预估中的应用[J]. 北京林业大学学报, 2019, 41(12): 23-36. Lei Xiangdong. Applications of machine learning algorithms in forest growth and yield prediction[J]. Journal of Beijing Forestry University, 2019, 41(12): 23-36. DOI:10.12171/j.1000-1522.20190356 |
| [34] |
李威. 基于机器学习的森林多源遥感数据分析方法研究[D]. 哈尔滨: 哈尔滨工程大学博士学位论文, 2018: 15-95. Li Wei. Research on Forest Remote Sensing Data Analysis Methodology Based on Machine Learning[D]. Harbin: The Doctoral Dissertation of Harbin Engineering University, 2018: 15-95. |
| [35] |
王文倩. 基于机器学习和零膨胀模型估算大兴安岭树种生物量[D]. 长春: 东北师范大学硕士学位论文, 2019: 16-35. Wang Wenqian. Predicting Species-level Biomass Using Machine Learning and Zero-inflated Models in the Great Xing'an Mountains[D]. Changchun: The Master's Dissertation of Northeast Normal University, 2019: 16-35. |
| [36] |
Xiang W H, Liu S H, Deng X W, et al. General allometric equations and biomass allocation of Pinus massoniana trees on a regional scale in Southern China[J]. Ecological Research, 2011, 26(4): 697-711. DOI:10.1007/s11284-011-0829-0 |
| [37] |
Fu L Y, Zeng W S, Tang S Z. Individual tree biomass models to estimate forest biomass for large spatial regions developed using four pine species in China[J]. Forest Science, 2017, 63(3): 241-249. DOI:10.5849/FS-2016-055 |
| [38] |
Fu Y, Lei Y C, Zeng W S, et al. Uncertainty assessment in aboveground biomass estimation at the regional scale using a new method considering both sampling error and model error[J]. Canadian Journal of Forest Research, 2017, 47(8): 1095-1103. DOI:10.1139/cjfr-2016-0436 |
| [39] |
Dong L H, Zhang L J, Li F R. Additive biomass equations based on different dendrometric variables for two dominant species(Larix gmelinii Rupr. and Betula platyphylla Suk.)in natural forests in the Eastern Daxing'an Mountains, Northeast China[J]. Forests, 2018, 9(5): 24. |
| [40] |
蔡会德, 农胜奇, 张伟, 等. 广西主要树种立木生物量模型的研建[J]. 林业资源管理, 2014(4): 58-61+66. Cai Huide, Nong Shengqi, Zhang Wei, et al. Modeling of standing tree biomass for main species of trees in Guangxi Province[J]. Forest Resources Management, 2014(4): 58-61+66. DOI:10.13466/j.cnki.lyzygl.2014.04.012 |
| [41] |
曾伟生. 我国杉木通用性立木生物量模型研究[J]. 中南林业调查规划, 2013, 32(4): 4-11+15. Zeng Weisheng. Generalized tree biomass equations of Chinese fir in China[J]. Central South Forest Inventory and Planning, 2013, 32(4): 4-11+15. DOI:10.3969/j.issn.1003-6075.2013.04.002 |
| [42] |
曾伟生. 基于木材密度的34个树种组一元立木生物量模型建立[J]. 林业资源管理, 2017(6): 41-46. Zeng Weisheng. Developing one-variable individual tree biomass models based on wood density for 34 tree species in China[J]. Forest Resources Management, 2017(6): 41-46. DOI:10.13466/j.cnki.lyzygl.2017.06.008 |
| [43] |
Liang W J, Hu H Q, Liu F J, et al. Research advance of biomass and carbon storage of poplar in China[J]. Journal of Forestry Research, 2006, 17(1): 75-79. DOI:10.1007/s11676-006-0018-0 |
| [44] |
Luo Y J, Wang X K, Ouyang Z Y. A China's normalized tree biomass equation dataset[DB/OL]. PANGAEA, 2018. doi: 10.1594/PANGAEA.895244.
|
| [45] |
罗云建, 王效科, 张小金, 等. 中国森林生态系统生物量及其分配研究[M]. 北京: 中国林业出版社, 2013: 115-191. Luo Yunjian, Wang Xiaoke, Zhang Xiaojin, et al. Biomass and Its Allocation of Forest Ecosystems in China[M]. Beijing: China Forestry Publishing, 2013: 115-191. |
| [46] |
国家林业局. LY/T 2259-2014, 立木生物量建模样本采集技术规程[S]. 北京: 中国标准出版社, 2015. The State Forestry Administration of the People's Republic of China. LY/T 2259-2014, Technical Regulation on Sample Collections for Tree Biomass Modeling[S]. Beijing: Standards Press of China, 2015. |
| [47] |
国家林业局. LY/T 2258-2014, 立木生物量建模方法技术规程[S]. 北京: 中国标准出版社, 2015. The State Forestry Administration of the People's Republic of China. LY/T 2258-2014, Technical Regulation on Methodology for Tree Biomass Modeling[S]. Beijing: Standards Press of China, 2015. |
| [48] |
Phillips D L, Brown S L, Schroeder P E, et al. Toward error analysis of large-scale forest carbon budgets[J]. Global Ecology and Biogeography, 2000, 9(4): 305-313. DOI:10.1046/j.1365-2699.2000.00197.x |
| [49] |
Enquist B J, West G B, Brown J H. Quarter-power allometric scaling in vascular plants: Functional basis and ecological consequences[M]//Brown J H, West G B. Scaling in Biology. Oxford: Oxford University Press, 2000: 167-170.
|
| [50] |
Kittredge J. Estimation of the amount of foliage of trees and stands[J]. Journal of Forestry, 1944, 42(12): 905-912. |
| [51] |
Parresol B R. Assessing tree and stand biomass: A review with examples and critical comparisons[J]. Forest Science, 1999, 45(4): 573-593. |
| [52] |
Ketterings Q M, Coe R, Noordwijk M V, et al. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests[J]. Forest Ecology and Management, 2001, 146(1): 199-209. |
| [53] |
Enquist B J, Niklas K J. Global allocation rules for patterns of biomass partitioning in seed plants[J]. Science, 2002, 295(5559): 1517-1520. DOI:10.1126/science.1066360 |
| [54] |
Suykens J A K, Gestel T V, Brabanter J D, et al. Least Squares Support Vector Machines[M]. Singapore: World Scientific, 2002: 71-116.
|
| [55] |
Suykens J A, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300. DOI:10.1023/A:1018628609742 |
| [56] |
孙宗海, 孙优贤. 用于回归估计的最小二乘广义支持向量机[J]. 系统工程理论与实践, 2004(7): 94-97. Sun Zonghai, Sun Youxian. Least square generalized support vector machines for regression[J]. System Engineering Theory and Practice, 2004(7): 94-97. DOI:10.3321/j.issn:1000-6788.2004.07.013 |
| [57] |
Brown S L, Schroeder P E. Spatial patterns of aboveground production and mortality of woody biomass for eastern U. S.forests[J]. Ecological Applications, 1999, 9(3): 968-980. |
| [58] |
Albaugh T J, Bergh J, Lundmark T, et al. Do biological expansion factors adequately estimate stand-scale aboveground component biomass for Norway spruce?[J]. Forest Ecology and Management, 2009, 258(12): 2628-2637. DOI:10.1016/j.foreco.2009.09.021 |
| [59] |
罗云建, 张小全, 王效科, 等. 森林生物量的估算方法及其研究进展[J]. 林业科学, 2009, 45(8): 129-134. Luo Yunjian, Zhang Xiaoquan, Wang Xiaoke, et al. Forest biomass estimation methods and their prospects[J]. Scientia Silvae Sinicae, 2009, 45(8): 129-134. DOI:10.3321/j.issn:1001-7488.2009.08.023 |
| [60] |
曾伟生. 全国立木生物量方程建模方法研究[D]. 北京: 中国林业科学研究院博士学位论文, 2011: 97-105. Zeng Weisheng. Methodology on Modeling of Single-tree Biomass Equations for National Biomass Estimation in China[D]. Beijing: The Doctoral Dissertation of Chinese Academy of Forestry, 2011: 97-105. |
| [61] |
曾伟生, 唐守正. 立木生物量方程的优度评价和精度分析[J]. 林业科学, 2011, 47(11): 106-113. Zeng Weisheng, Tang Shouzheng. Goodness evaluation and precision analysis of tree biomass equations[J]. Scientia Silvae Sinicae, 2011, 47(11): 106-113. DOI:10.11707/j.1001-7488.20111117 |
| [62] |
曾伟生, 陈新云, 杨学云. 我国人工杨树生物量建模和生产力分析[J]. 林业科学, 2019, 55(11): 1-8. Zeng Weisheng, Chen Xinyun, Yang Xueyun. Biomass modeling and productivity analysis of planted Populus spp. in China[J]. Scientia Silvae Sinicae, 2019, 55(11): 1-8. DOI:10.11707/j.1001-7488.20191101 |
| [63] |
Bi H Q, Birk E, Turner J, et al. Converting stem volume to biomass with additivity, bias correction, and confidence bands for two Australian tree species[J]. New Zealand Journal of Forestry Science, 2001, 31(3): 298-319. |
| [64] |
Brown S, Lugo A E. Biomass of tropical forests: A new estimate based on forest volumes[J]. Science, 1984, 223(4642): 1290-1293. DOI:10.1126/science.223.4642.1290 |
| [65] |
Lehtonen A, Mäkipää R, Heikkinen J, et al. Biomass expansion factors(BEFs)for Scots pine, Norway spruce and birch according to stand age for boreal forests[J]. Forest Ecology and Management, 2004, 188(1-3): 211-224. DOI:10.1016/j.foreco.2003.07.008 |
| [66] |
Zhou X P, Hemstrom M A. Estimating Aboveground Tree Biomass on Forest Land in the Pacific Northwest: A Comparison of Approaches[R]. Portland: U. S. Department of Agriculture, Forest Service, Pacific Northwest Research Station, 2009: 2-11. doi: 10.2737/PNW-RP-584.
|
| [67] |
华萌萌, 尹君, 胡召玲, 等. 基于机器学习的历史气候重建论文智能识别与数据挖掘初探[J]. 第四纪研究, 2021, 41(2): 550-561. Hua Mengmeng, Yin Jun, Hu Zhaoling, et al. Preliminary study on machine learning-based intelligent recognition of historical climate reconstruction papers and data mining[J]. Quaternary Sciences, 2021, 41(2): 550-561. |
| [68] |
Dong L H, Liu Y S, Zhang L J, et al. Variation in carbon concentration and allometric equations for estimating tree carbon contents of 10 broadleaf species in natural forests in Northeast China[J]. Forests, 2019, 10(928): 10. |
| [69] |
冯慧想. 杨树人工林生长特性及生物量研究[D]. 北京: 中国林业科学研究院硕士学位论文, 2007: 39-55. Feng Huixiang. A Study on Growth Characteristic and Biomass of Poplar Plantation[D]. Beijing: The Master's Dissertation of Chinese Academy of Forestry, 2007: 39-55. |
| [70] |
董利虎, 李凤日, 贾炜玮. 东北林区天然白桦相容性生物量模型[J]. 林业科学, 2013, 49(7): 75-85. Dong Lihu, Li Fengri, Jia Weiwei. Compatible tree biomass models for natural white birch(Betula platyphylla)in Northeast China forest area[J]. Scientia Silvae Sinicae, 2013, 49(7): 75-85. |
| [71] |
Zhang C, Peng D L, Huang G S, et al. Developing aboveground biomass equations both compatible with tree volume equations and additive systems for single-trees in poplar plantations in Jiangsu Province, China[J]. Forests, 2016, 7(32): 2. |
| [72] |
Lambert M C, Ung C, Raulier F. Canadian national tree aboveground biomass equations[J]. Canadian Journal of Forest Research, 2005, 35(8): 1996-2018. DOI:10.1139/x05-112 |
2 Zhejiang Jinhua Mountain Observation and Research Station for Subtropical Forest Ecosystems, Jinhua 321004, Zhejiang)
Abstract
Forest ecosystems play important roles in global vegetation and carbon cycles. Rapid and accurate estimation of large-scale forest biomass is important in estimating global forest carbon storage and mitigating anthropogenic global climate change.In this study, we collected biomass data(including biomass and biomass equations for trunk, leaves, branches, roots and other parts of the tree) of the dominant tree species of 461 research sites in China(excluding Hong Kong, Macao, and Taiwan) from 287 articles published from 1982 to 2019. Three methods, namely, basic biomass model, least square support vector machine(LSSVM) model, and dummy variable model, were adopted to establish general biomass allometric equations for deciduous broadleaf species, evergreen broadleaf species, and coniferous species. The goodness evaluation and precision analysis of these different methods were conducted.Biomass estimation using the general allometric equations established by the three methods achieved high prediction accuracy. Thus, these general allometric equations could be used to estimate forest biomass in China. The basic biomass model ignored the influence of non-tree measurement factors other than tree diameter at breast height (D) and height (H), whereas the simulated results presented the greatest uncertainty. The LSSVM model optimized the parameters, thereby improving the precision of model simulation. The dummy variable model affected various categorical factors, such as environmental indicators, reduced the influence of environmental factors, and improved the applicability of the model. Aboveground biomass allometric equations, which considered both the D and H variables(D2 H), presented a higher prediction accuracy than the equations that considered the D variable only. Similarly, belowground biomass allometric equations, which considered the D variable only, achieved a high prediction accuracy. This study demonstrated that integrating different modeling methods into biomass estimation is necessary to improve the accuracy of large-scale biomass estimates. This endeavor is the future direction of biomass evaluation. 2021, Vol.41
2021, Vol.41

