似大地水准面作为正常高系统的参考面,是由地面沿垂线向下量取正常高所得点形成的连续曲面,无明显物理意义。而大地水准面是与平均海水面密合的重力等位面,反映地球重力场的几何表象,作为正高系统的参考面。多数国家的法定高程基准属于区域性高程基准,不同高程基准之间不仅存在基准位差,也存在正常高和正高系统差异,导致不同国家地理信息成果难以满足跨境工程建设需求[1]。
正常高与正高的转换等价于似大地水准面与大地水准面的转换,而似大地水准面与大地水准面转换的关键是求取地形内部沿铅垂线方向的平均重力值,但这涉及地球内部密度问题,难以严密求解。赫尔默特法计算平均重力值是基于珀雷归算求取地球内部重力值,采用布格片近似代替地形质量,进而求得由布格异常近似计算的似大地水准面与大地水准面的转换关系[2]。但近似方法现在已经难以满足精度要求,其在山区存在较大误差[3]。将地球内部重力值在对应地面点进行泰勒级数展开,则可由实际重力梯度表达,但需要在近似转换的基础上增加扰动重力梯度改正项[4-5]。上述思路都是先表达地球内部重力,然后积分求解平均重力值,但内部重力值存在复杂的非线性变化,在地形复杂地区难以精确求解。将内部重力值分解为正常重力、地形引力、布格扰动重力,将地形引力用地形引力位表示,则积分求取平均重力时,地形引力项积分结果直接变成地形引力位之差,可使计算更加严密[6-9]。
为研究复杂地形条件下似大地水准面与大地水准面的转换改正,本文选择珠峰地区为实验区,利用严密转换公式进行计算,分析各项改正的数值影响大小及其与地形起伏变化的相关性。顾及不同改正项的影响,计算不同近似程度下转换改正的数值区间,分析其空间变化特征。
1 转换方法根据正高和正常高的定义,可得出似大地水准面与大地水准面的关系为[4]:
| $ N-\zeta=\frac{\bar{g}-\bar{\gamma}}{\bar{\gamma}} h $ | (1) |
式中,N为大地水准面差距,ζ为高程异常,γ为椭球面至似地形表面间的平均正常重力,g为大地水准面至地面的平均重力,h为正高。
由于平均重力g难以严密求出,在一定的近似条件下,可利用布格重力异常简化计算[2]:
| $ N-\zeta \approx \frac{\Delta g_{\mathrm{B}}}{\bar{\gamma}} h $ | (2) |
式中,ΔgB为布格重力异常。
在山区利用式(2)进行计算将引起较大误差。顾及地形质量影响和重力改正后,可采用更加严密的似大地水准面与大地水准面转换方法[8-10]:
| $ N-\zeta \approx \frac{\Delta g_{\mathrm{B}}}{\bar{\gamma}} h+\frac{V_0^{\mathrm{t}}-V^{\mathrm{t}}}{\bar{\gamma}}-\frac{h^2}{2 \bar{\gamma}} \frac{\partial \Delta g_{\mathrm{B}}}{\partial h} $ | (3) |
式中,Vt为地面点的地形引力位,Vt0为大地水准面上投影点的地形引力位。式(3)转换可分为3部分,分别为由布格重力异常计算的重力改正、由地形引力位差计算的地形位差改正和由布格重力异常梯度计算的重力梯度改正。
布格重力异常ΔgB计算公式为:
| $ \Delta {g_{\rm{B}}} = \Delta g - 2{\rm{\pi }}G{\rho _0}h + {\rm{d}}{g_{tc}} $ | (4) |
式中,Δg为地面重力异常,G为引力常数,ρ0为平均地壳密度,dgtc为局部地形改正。布格重力异常梯度计算公式为:
| $ \left(\frac{\Delta g_{\mathrm{B}}}{\partial h}\right)_P \approx \frac{R^2}{2 \pi} \iint \frac{\Delta g_{\mathrm{B}}-\left(\Delta g_{\mathrm{B}}\right)_P}{l_0^3} \mathrm{~d} \sigma-\frac{2}{R}\left(\Delta g_{\mathrm{B}}\right)_P $ | (5) |
式中,l0为计算点P到流动面元R2dσ的距离,(ΔgB)P为P点布格重力异常。
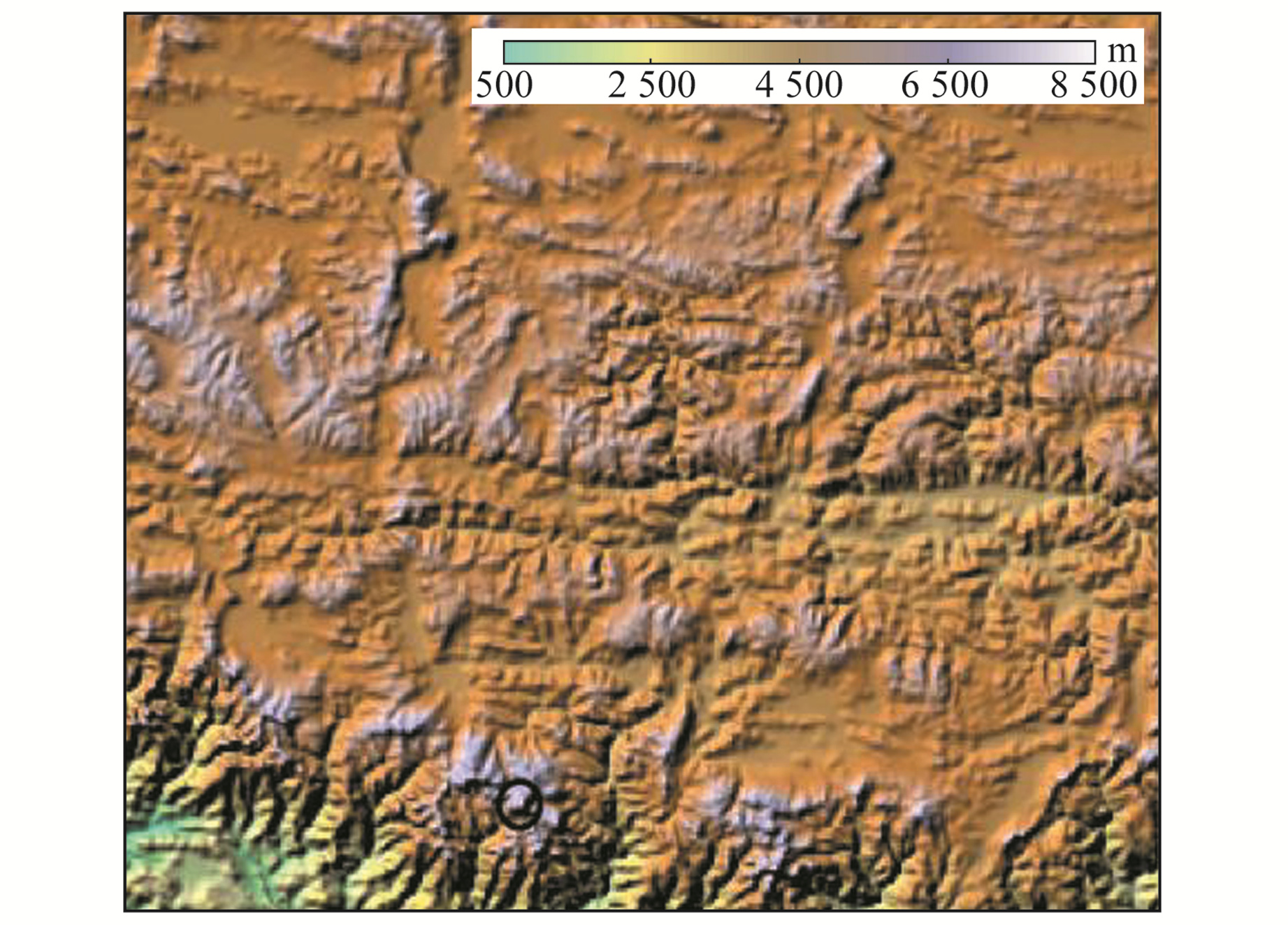
2 数值实验与分析为验证和分析似大地水准面与大地水准面转换方法各改正项的数值影响大小,选择地形起伏大的珠峰地区4°×5°范围为实验区,利用收集的地面重力点数据,采用地形均衡归算进行内插格网化后,恢复1′×1′格网空间重力异常,用于计算布格重力异常和布格重力异常梯度。地形数据使用国际农业研究磋商组织下属的空间信息协会发布的3″分辨率高程数据集SRTM v4.1,该版本数据经过插值与补洞处理后,高程质量有显著改善。所选区域最高点为珠峰峰顶(图 1圆圈所示位置),整个区域平均高程4 794 m,最低点与最高点相差7 699 m。
|
图 1 实验区地形高程 Fig. 1 Topographic height of the experimental area |
将地形数据平均为1′×1′分辨率,结合同等分辨率实测重力异常格网数据,利用式(3)计算似大地水准面与大地水准面转换的3项改正值,其中布格重力异常利用式(4)计算,根据棱柱积分法分别计算地形质量在地面点和大地水准面上投影点产生的引力位,布格重力异常梯度按照式(5)计算,统计结果见表 1(单位m)。分3种情况统计转换改正:(N-ζ)1表示仅考虑第1项重力改正计算;(N-ζ)2表示同时考虑重力改正和地形位差改正;(N-ζ)3表示考虑全部3项改正。图 2~4分别对应3种情况计算的转换改正值。
|
|
表 1 计算结果统计 Tab. 1 Statistics of calculation results |

|
图 2 仅考虑重力改正的计算结果 Fig. 2 Calculation results only considering gravity correction |
|
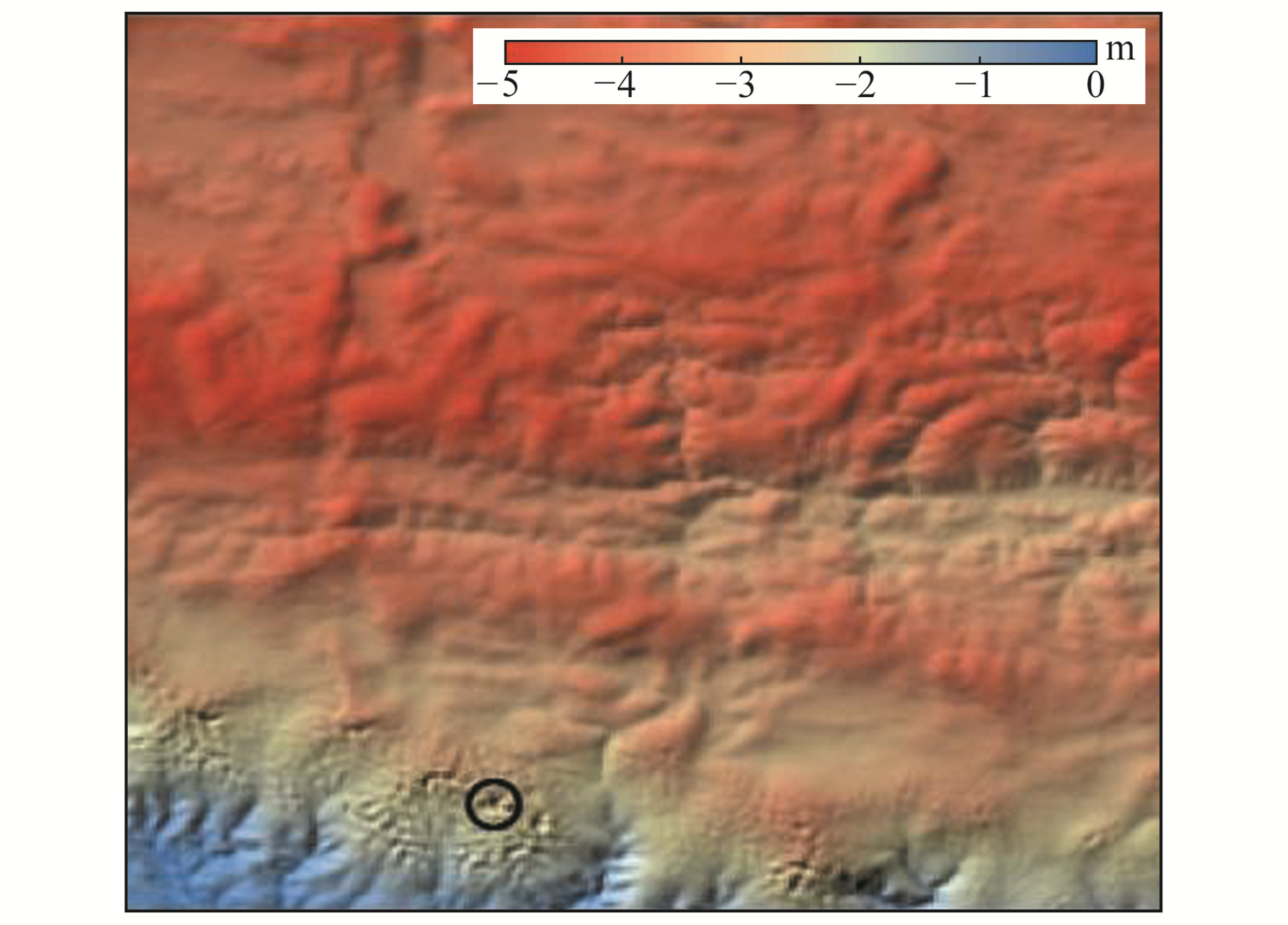
图 3 顾及重力改正和地形位差改正的计算结果 Fig. 3 Calculation results considering gravity correction and terrain correction |
|
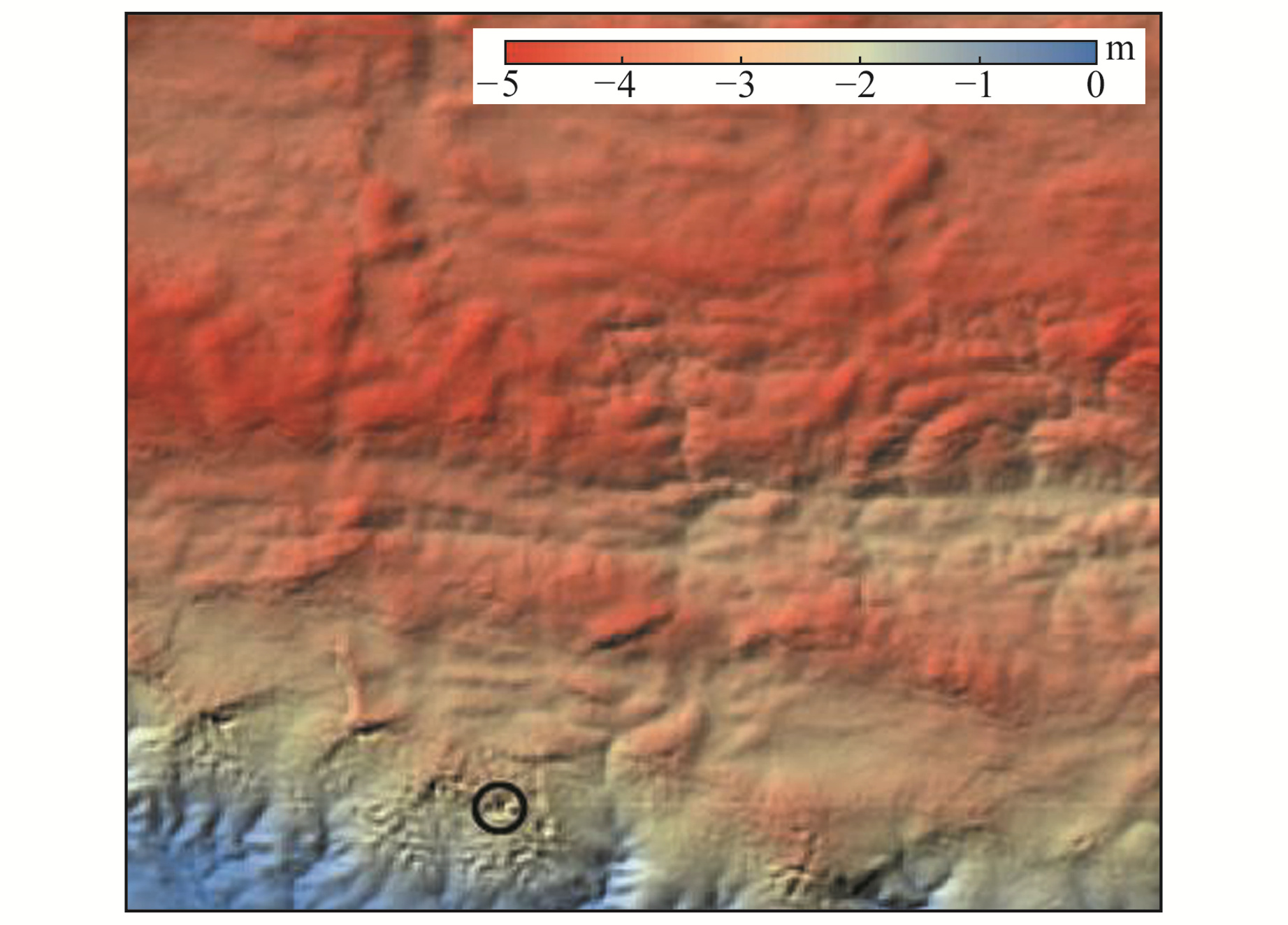
图 4 顾及3种改正的计算结果 Fig. 4 Calculation results considering three corrections |
从表 1可以看出,地形位差改正项量级较大,实验区极值达到1.272 m,而重力梯度改正项相对较小,实验区范围极值为-0.138 m。由图 1、2可知,仅考虑布格异常近似计算转换改正结果与地形具有较强的相关性。在顾及地形改正项时,图 3相较于图 2更为平滑,表 1也显示标准差有所下降,基本变化趋势与地形相符,但局部特征发生较大变化,如圆圈所示峰顶位置。当增加重力改正项时,图 4与图 3表现基本一致,表 1也显示二者统计结果变化较小。
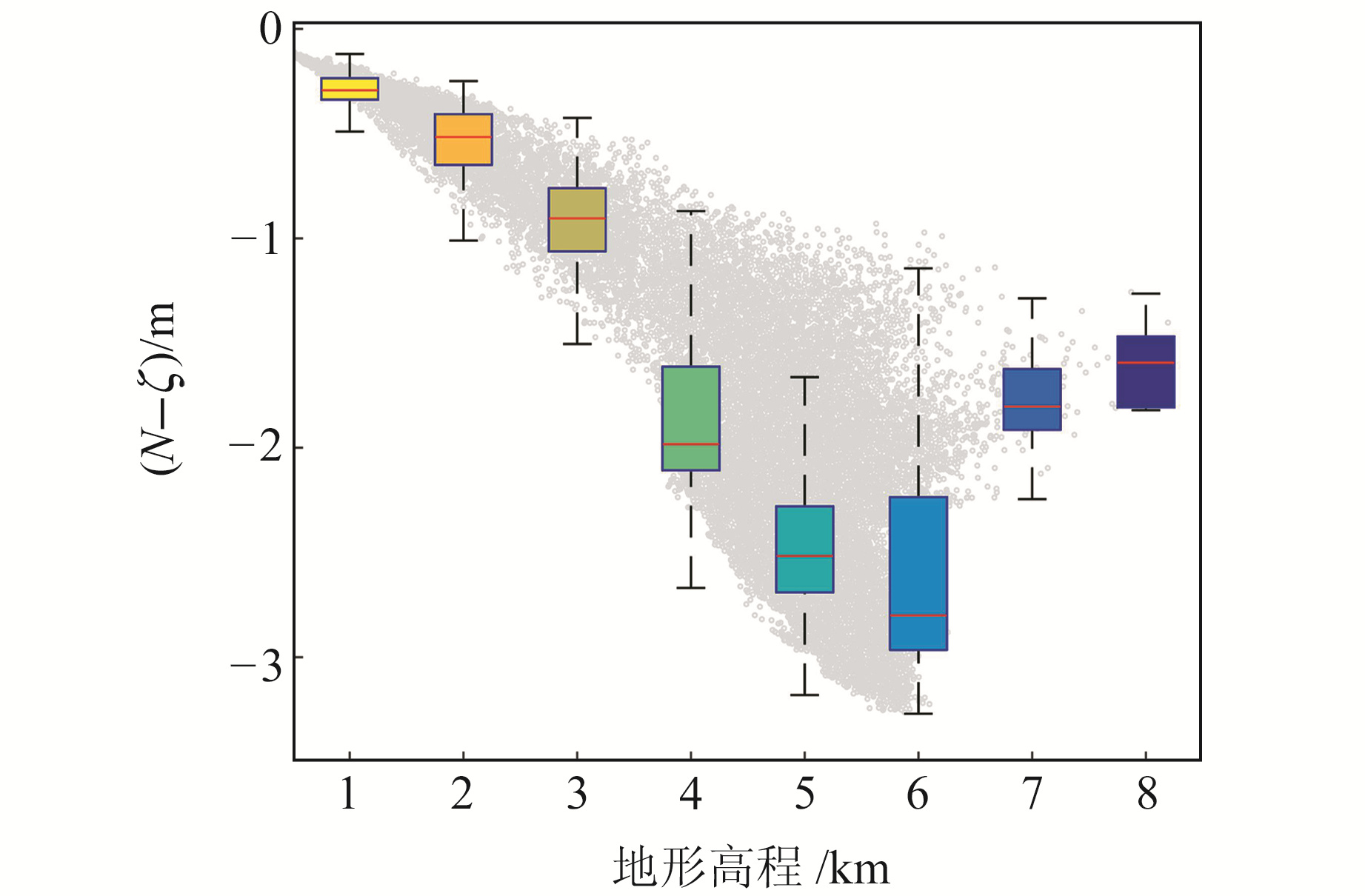
对顾及地形改正和重力改正的严密计算结果,按照地形从500~8 500 m范围,以1 000 m为间隔分为8组,统计并绘制箱线图(图 5)。由图可知,转换改正值并不完全与地形成正比,第6组(高程5 500~6 500 m)改正值中位数最大,数值变化范围也最大。
|
图 5 高程分区严密计算转换统计 Fig. 5 Height zoning statistics according to strict formula |
为进一步分析3项改正值与地形的局部变化特征,在峰顶沿东西方向和南北方向绘制剖面,结果见图 6、7。为直观显示转换改正与地形的变化趋势,本文使用高程异常与大地水准面高之差,与前文符号相反。

|
图 6 地形与转换改正东西方向剖面 Fig. 6 Terrain and correction profile in the east-west direction |
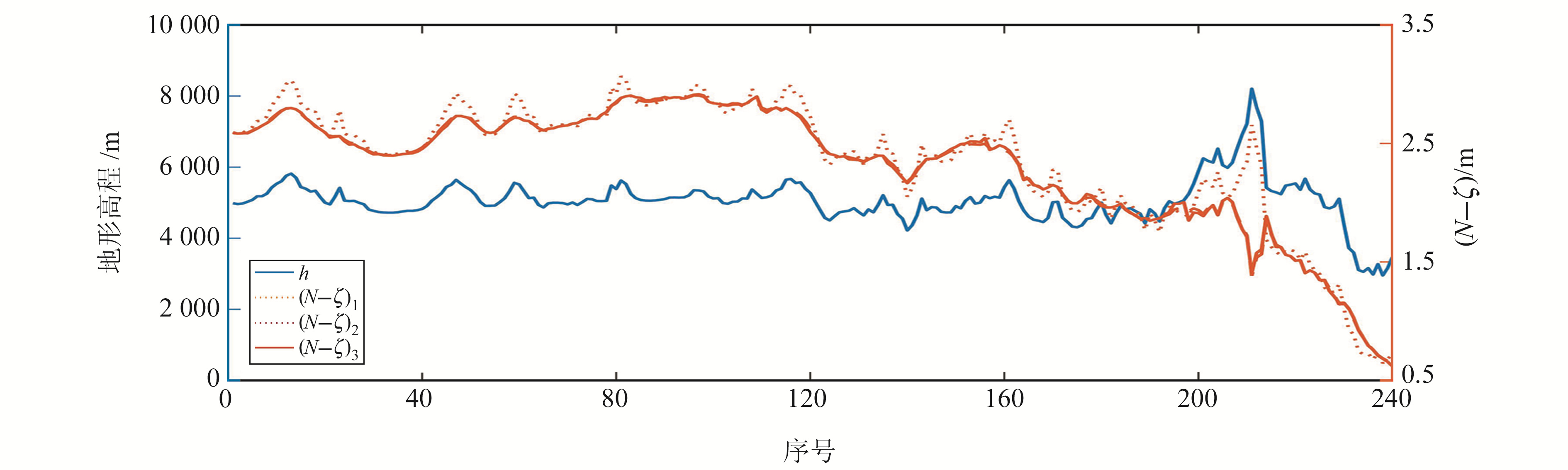
|
图 7 地形与转换改正南北方向剖面 Fig. 7 Terrain and correction profile in the north-south direction |
图 6、7同样表明,仅考虑布格异常近似计算结果与地形变化具有相近性,顾及地形改正项与同时顾及地形、重力改正项基本重叠,仅存在细微变化,但与仅考虑布格异常近似计算结果相比,局部范围趋势相反。该结果与Flury等[7]的结果一致,主要是由于地形引力位差改正项在山顶和山谷趋势不同,导致似大地水准面与大地水准面转换改正的极值可能出现在山顶或山谷附近。
3 结语采用实测重力数据和高分辨率地形数据计算珠峰地区似大地水准面和大地水准面转换,分析顾及不同改正项时转换的数值大小及其与地形的相关性。结果表明,重力改正项是转换的主项,地形位差改正和重力梯度改正项影响显著,在复杂山区不可忽略。仅考虑布格重力异常近似计算结果与地形具有较强相关性,顾及地形位差改正后相关性降低,局部区域与地形反相关,再顾及重力梯度改正时,变化不显著。
| [1] |
党亚民, 蒋涛, 陈俊勇. 全球高程基准研究进展[J]. 武汉大学学报: 信息科学版, 2022, 47(10): 1 576-1 586 (Dang Yamin, Jiang Tao, Chen Junyong. Review on Research Progress of the Global Height Datum[J]. Geomatics and Information Science of Wuhan University, 2022, 47(10): 1 576-1 586)
(  0) 0) |
| [2] |
Heiskanen W A, Moritz H. Physical Geodesy[M]. San Francisco: Freeman and Company, 1967
(  0) 0) |
| [3] |
张赤军. 论(N-ζ)公式的内涵及推求N的精度[J]. 武汉大学学报: 信息科学版, 2005, 30(6): 471-473 (Zhang Chijun. Content and Precision Determining of Difference between Geoid and Quasigeoid[J]. Geomatics and Information Science of Wuhan University, 2005, 30(6): 471-473)
(  0) 0) |
| [4] |
李建成, 陈俊勇, 宁津生, 等. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003 (Li Jiancheng, Chen Junyong, Ning Jinsheng, et al. Earth Gravity Field Approximation Theory and Determination of the Chinese 2000 Qusigeoid[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [5] |
徐新强, 赵德军, 楼楠. 顾及高程二次项的大地水准面与似大地水准面之差距[J]. 大地测量与地球动力学, 2013, 33(5): 75-78 (Xu Xinqiang, Zhao Dejun, Lou Nan. A Geoid to Quasigeoid Separation Considering Second Order Height Terms[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 75-78)
(  0) 0) |
| [6] |
Tenzer R, Vaní Ač ek P, Santos M, et al. The Rigorous Determination of Orthometric Heights[J]. Journal of Geodesy, 2005, 79(1): 82-92
(  0) 0) |
| [7] |
Flury J, Rummel R. On the Geoid-Quasigeoid Separation in Mountain Areas[J]. Journal of Geodesy, 2009, 83(9): 829-847 DOI:10.1007/s00190-009-0302-9
(  0) 0) |
| [8] |
Sjöberg L E. A Strict Formula for Geoid-to-Quasigeoid Separation[J]. Journal of Geodesy, 2010, 84(11): 699-702 DOI:10.1007/s00190-010-0407-1
(  0) 0) |
| [9] |
Wang Y M, Veronneau M, Huang J L, et al. Accurate Computation of Geoid-Quasigeoid Separation in Mountainous Region——A Case Study in Colorado with Full Extension to the Experimental Geoid Region[J]. Journal of Geodetic Science, 2023, 13(1)
(  0) 0) |
| [10] |
Sjöberg L E. The Geoid-to-Quasigeoid Difference Using an Arbitrary Gravity Reduction Model[J]. Studia Geophysica et Geodaetica, 2012, 56(4): 929-933 DOI:10.1007/s11200-011-9037-1
(  0) 0) |
 2024, Vol. 44
2024, Vol. 44


