2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 西安测绘研究所,西安市雁塔路中段1号,710054;
4. 西南石油大学土木工程与测绘学院,成都市新都大道8号,610500;
5. 陆军勤务学院,重庆市北一路20号,401311
大气、海洋、陆地水等地表质量变化会产生明显的负荷响应,引起地表垂直形变和地球重力场变化[1]。研究地表负荷形变可了解大气、海洋和陆地水等地表质量变化及其相互作用信息,对全球气候变化和地球动力学研究具有重要意义。GNSS技术的发展,特别是GPS技术的发展,可为实时连续监测地表形变提供有效的技术手段,可通过其连续观测的站点坐标时间序列反映地表垂直形变。已有研究表明,扣除构造运动等引起的长期变化后,GPS垂直位移时间序列的周年变化主要由地表物质迁移所引起[2-4]。
重力场恢复与气候实验卫星(GRACE)于2002-03成功发射,在陆地水储量等地表物质迁移研究中得到广泛应用,其时变重力数据不仅可用于反演得到地表物质迁移,也可计算相应变化引起的地表垂直负荷形变。因此,联合GPS和GRACE两种观测手段,可定量对比分析垂直形变特征。国内外学者对GPS垂直位移和GRACE垂直形变进行过大量研究,相关结果表明,对于负荷形变明显的区域,GPS垂直位移与GRACE垂直形变时间序列总体上具有较好的一致性[3-8],其差异主要是由GPS观测误差和数据处理方法等因素造成[8-10]。
本文对陕甘宁地区地表垂直形变特征进行研究,采用研究区内甘肃省CORS网和中国大陆构造环境监测网络中共48个台站的观测数据,解算得到观测台站的垂直位移,并与GRACE时变重力场Mascon模型解CSR RL05M数据计算得到的垂直形变进行对比分析,研究环境负荷对GPS垂直位移时间序列的影响,总结分析研究区域的垂直形变特征,为合理分析该地区地表质量迁移提供重要依据。
1 数据及其处理 1.1 GPS数据及其处理选用原甘肃省测绘地理信息局CORS网和中国大陆构造环境监测网络中共48个观测台站的GPS连续观测数据,时间跨度为2013-09~2016-12。观测台站坐标解算采用分布式并行化GNSS数据处理软件GNSSer[11],数据处理具体策略为:采用精密单点定位(PPP)模式和双频消电离层组合观测值的观测模型;卫星截止高度角取10°;卫星轨道与钟差采用IGS 15 min精密星历和5min精密钟差;天线相位中心改正采用IGS14.atx改正;固体潮、极潮改正采用IERS2010模型,海潮改正采用FES2014模型;相对论效应考虑周期性相对论钟差、Sagnac效应和广义相对论引力延迟;电离层改正采用双频消电离层组合消除;对流层延迟改正采用VMF1映射函数及全球气压和温度模型GPT2。具体参数与模型设置见表 1。
|
|
表 1 解算所用模型和参数设置 Tab. 1 Parameters and models of data processing |
采用上述解算策略和模型,解算得到测站的单日解,再将单日解转换得到ITRF2014框架下的垂直分量时间序列。
1.2 GRACE数据及其处理地表质量变化引起的负荷响应与其位的变化密切相关。可将质量源看作一个整体,利用球谐函数展开计算位的变化,再通过位的变化求解质量变化引起的负荷响应[12]。基于地球负荷形变和地球重力场理论,可推导出地表负荷引起的垂直形变球谐函数计算公式为[13]:
| $ \begin{array}{l} u{\rm{ = }}\sum\limits_{n = 0}^{{N_{{\rm{max}}}}} {\frac{{3{\rho _w}}}{{{\rho _e}}} \cdot \frac{{{h^\prime}_n}}{{2n + 1}}\sum\limits_{m = 0}^n {(\Delta C_{nm}^h{\rm{cos}}m\lambda + } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta S_{nm}^h{\rm{sin}}m\lambda ){\overline P _{nm}}({\rm{cos}}\theta ) \end{array} $ | (1) |
式中,ρw为水密度,ρe为地球平均密度,h′n为负荷勒夫数,Nmax为球谐函数截断最大阶数,ΔCnmh、ΔSnmh为表面负荷Δhw的球谐函数展开的斯托克斯系数。
将式(1)进行变换,可得到利用时变重力场模型计算的由地表质量变化引起的垂直形变为:
| $ \begin{array}{l} u{\rm{ = }}R\sum\limits_{n = 0}^{{N_{{\rm{max}}}}} {\frac{{{h^\prime}_n}}{{{k^\prime}_n + 1}}\sum\limits_{m = 0}^n {(\Delta C_{nm}^{}{\rm{cos}}m\lambda + } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta S_{nm}^{}{\rm{sin}}m\lambda {\overline P _{nm}}({\rm{cos}}\theta ) \end{array} $ | (2) |
采用美国CSR发布的Mascon模型解CSR RL05M数据[14],时间跨度为2002-04~2017-06。CSR RL05M数据解算时C20项采用SLR数据替换,地心1阶项采用GRACE卫星和海洋模型联合估计得到,冰后回弹改正采用三维压缩地表负荷滞弹响应模型,CSR RL05M数据采用NetCDF格式以0.5°分辨率格网形式发布。由于Mascon模型解在解算时已通过约束消除条带噪声影响,因此不需要再用滤波方法对CSR RL05M数据进行处理,本文直接将CSR RL05M数据转换为100阶球谐系数模型数据。为了与GPS垂直位移包含的地球物理信号一致,计算时采用非潮汐大气海洋去混频模型(AOD1B)数据[15]GAC加回至GRACE时变重力场模型数据。
2 讨论分析 2.1 评价指标 2.1.1 相关系数两种不同空间技术获取的时间序列,其周期项若相关,则存在以下可能:1)2个周期实为同一周期,即由同一个物理因素所引起,由于所采用的分析方法不同或分辨率等限制而显现出2个周期;2)引起2个周期项的物理因素之间具有相关性。因此,可采用GPS垂直位移和GRACE垂直形变间的相关性来判断两者是否为同一周期项,或为同一物理因素引起的周期变化[16]。
相关系数计算公式为:
| $ r = \frac{{\sum\limits_{i = 1}^n {(u_i^{{\rm{GPS}}} - \bar u_i^{{\rm{GPS}}})(u_i^{{\rm{GRACE}}} - \bar u_i^{{\rm{GRACE}}})} }}{{\sqrt {\sum\limits_{i = 1}^n {{{(u_i^{{\rm{GPS}}} - \bar u_i^{{\rm{GPS}}})}^2}\sum\limits_{i = 1}^n {{{(u_i^{{\rm{GRACE}}} - \bar u_i^{{\rm{GRACE}}})}^2}} } } }} $ | (3) |
式中,ui为垂直位移观测值,n为观测值个数,为观测值均值。相关系数可定量刻画2个信号的相似程度,相关系数对信号相位较为敏感,取值区间为[-1, 1],系数越接近1表明2个信号的时间序列相关性越强。
2.1.2 加权均方根减少量加权均方根(weight root mean squares,WRMS)减少量为移除GRACE垂直形变后的GPS垂直位移时间序列的加权均方根误差减少量与原GPS时间序列加权均方根误差的比值,可反映GRACE垂直形变对GPS垂直位移的贡献:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{WRMS}}\left( r \right) = \\ \frac{{{\rm{WRMS}}({u^{{\rm{GPS}}}}) - {\rm{WRMS}}({u^{{\rm{GPS}}}} - {u^{{\rm{GRACE}}}})}}{{{\rm{WRMS}}({u^{{\rm{GPS}}}})}} \end{array} $ | (4) |
当认为所有观测值等权时,加权均方根减少量则为均方根减少量。由于GRACE垂直形变的中误差难以估算,同时考虑到WRMS和RMS在表达信号的一致性上基本相同,本文将采用RMS减少量作为评价GPS垂直位移和GRACE垂直形变相关性的指标。
2.1.3 周年信号减少量GPS坐标时间序列不仅可以反映出台站的趋势变化,还可以反映出台站存在的非线性变化。趋势变化主要反映台站受同一区域构造应力场控制下的继承性构造运动,而非线性变化主要反映台站受到的非潮汐海洋负载、大气负载、水文负载等地壳物理效应作用。已有研究表明,包括非潮汐海洋负载、大气负载、水文负载在内的环境负载是造成台站非线性变化的主要因素[2]。而环境负载形变序列中如非潮汐海洋负载及陆地水负载也存在线性趋势,由于无法确定其是真实信号还是未知的系统误差,一般不予考虑,需要去除其中的趋势项[17]。因此,对GPS垂直位移和GRACE垂直形变进行对比时,需要扣除GPS垂直位移中的长期趋势信号。GPS单站、单分量时间序列一般采用下列周期项数学模型进行表示[16]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y({t_i}) = a + b{t_i} + c{\rm{sin}}(2\pi {t_i}) + d{\rm{cos}}(2\pi {t_i}) + \\ e{\rm{sin}}(4\pi {t_i}) + f{\rm{cos}}(4\pi {t_i}) + \sum\limits_{j = 1}^{{n_g}} {{g_j}H({t_i} - {T_{{g_j}}})} + {\upsilon _i} \end{array} $ | (5) |
式中,ng表示有ng个阶跃发生,ti为观测时间,a为常数项,b为线性趋势项,c、d、e、f可分别描述周年和半周年振幅,gj为地震等造成的偏移,gjH(ti-Tgj)为阶跃函数,υi为残差值。
通过下式拟合去除长期趋势项后的垂直位移:
| $ \begin{array}{l} u = {A_1}{\rm{sin}}(2\pi (t - {t_0}) + {\varphi _1}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_1}{\rm{sin}}(4\pi (t - {t_0}) + {\varphi _2}) \end{array} $ | (6) |
式中,A1和A2分别为去除趋势项的周年和半周年振幅,φ1和φ2分别为周年和半周年信号的初始相位,t0为初始相位。周年信号减少量(annual amplitude reduction,AAr)可用来评价季节性信号的一致性,定义为:
| $ {\rm{AAr}} = \frac{{{\rm{AA}}({u^{{\rm{GPS}}}}) - {\rm{AA}}({u^{{\rm{GPS}}}} - {u^{{\rm{GRACE}}}})}}{{{\rm{AA}}({u^{{\rm{GPS}}}})}} $ | (7) |
相比于均方根误差减少量,周年信号减少量不易受随机误差影响。
相关系数对相位敏感,但无法评价时间序列变化振幅是否一致;均方根误差减少量和周年信号减少量虽然能够同时顾及振幅和相位,但均方根误差减少量受随机噪声影响较大,而周年信号减少量则无法兼顾非谐波季节性信号[18]。因此,单一指标均具有一定的局限性,需要利用3个指标来综合评价GPS垂直位移和GRACE垂直形变的一致性。
2.2 结果与分析图 1为研究区内部分台站去除趋势项后垂直位移的时间序列结果,红色为GPS单日解,绿色为GPS垂直位移单月值,蓝色为GRACE垂直形变。从图中可以看出,PLCX、PLHT、QYTQ等台站GPS垂直位移和GRACE垂直形变时间序列具有较好的一致性,呈现显著的季节性周期变化。

|
图 1 部分台站GPS垂直位移和GRACE垂直形变时间序列 Fig. 1 GPS vertical displacement and GRACE vertical deformations time series of some stations |
图 2为研究区内台站垂直位移周年变化矢量图,红色为GPS垂直位移,蓝色为GRACE垂直形变,箭头代表周年振幅,箭头方向代表初始相位(从正东方向逆时针,相位起点为1月份)。从图中结果可以看出,GSGL(102.89°E,37.45°N)、LNMY(105.80°E,34.09°N)和LNLH(105.32°E,33.13°N)等台站周年信号与研究区内其他台站结果存在较大差异,其他台站GPS垂直位移和GRACE垂直形变一致性较好。
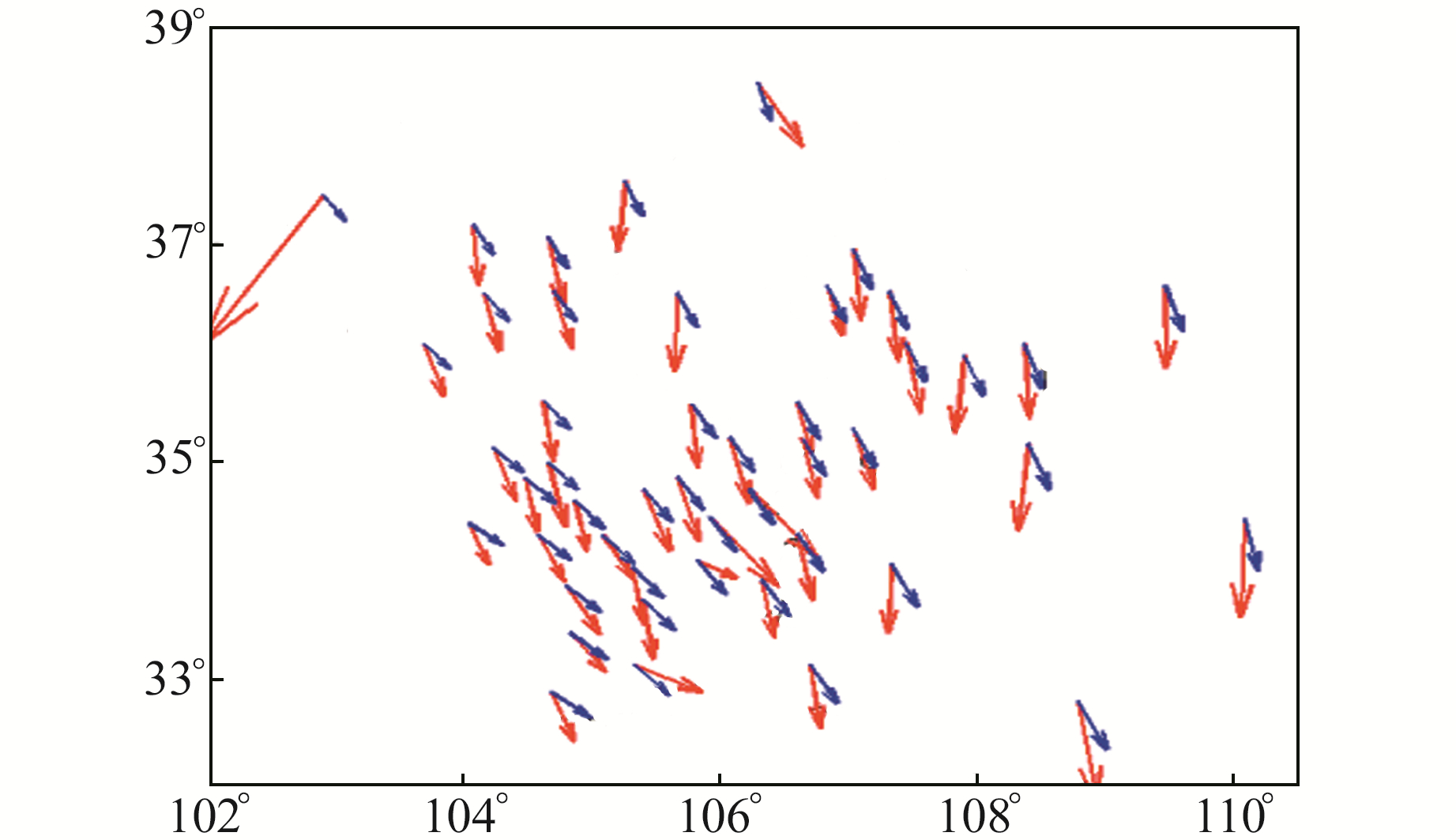
|
图 2 观测台站垂直位移周年变化矢量 Fig. 2 Annual variation vector of vertical displacement of observation stations |
图 3为研究区内各台站GPS垂直位移与GRACE垂直形变时间序列的相关系数。从图中结果可以看出,除个别台站外,大多数台站GPS垂直位移与GRACE垂直形变时间序列的相关系数均大于0.6,表明两者存在一定的相关性,但相关性在整个研究区域存在一定差异,在甘肃庆阳、平凉地区(35°~37°N,106.5°~108.5°E)相关系数比其他地区大。

|
图 3 观测台站GPS垂直位移和GRACE垂直形变相关系数 Fig. 3 Correlation coefficient between GPS vertical displacement and GRACE vertical deformation of observation stations |
图 4为研究区内各台站GPS垂直位移时间序列均方根误差减小值。从图中结果可见,除个别台站外,大多数台站垂直位移时间序列加权均方根误差减小量为0.2~0.5,表明在研究区内GPS垂直位移时间序列包含的非构造形变干扰中,约20%~50%是由于环境负载引起的负荷形变。均方根减少量在整个研究区内表现出与图 3相同的局部特征,即在甘肃庆阳、平凉地区(35°~37°N,106.5°~108.5°E)均方根减少量明显比其他地区大。

|
图 4 观测台站均方根减少量 Fig. 4 RMS reduction of observation stations |
图 5为研究区内各台站周年信号减少量,从图中可以看出,除个别台站外,研究区内大多数台站的垂直位移时间序列的周年信号减少量约为0.4~0.6,周年信号减少量较为明显。在甘肃庆阳、平凉地区(35°~37°N,106.5°~108.5°E)周年信号减少量也明显比其他地区大。
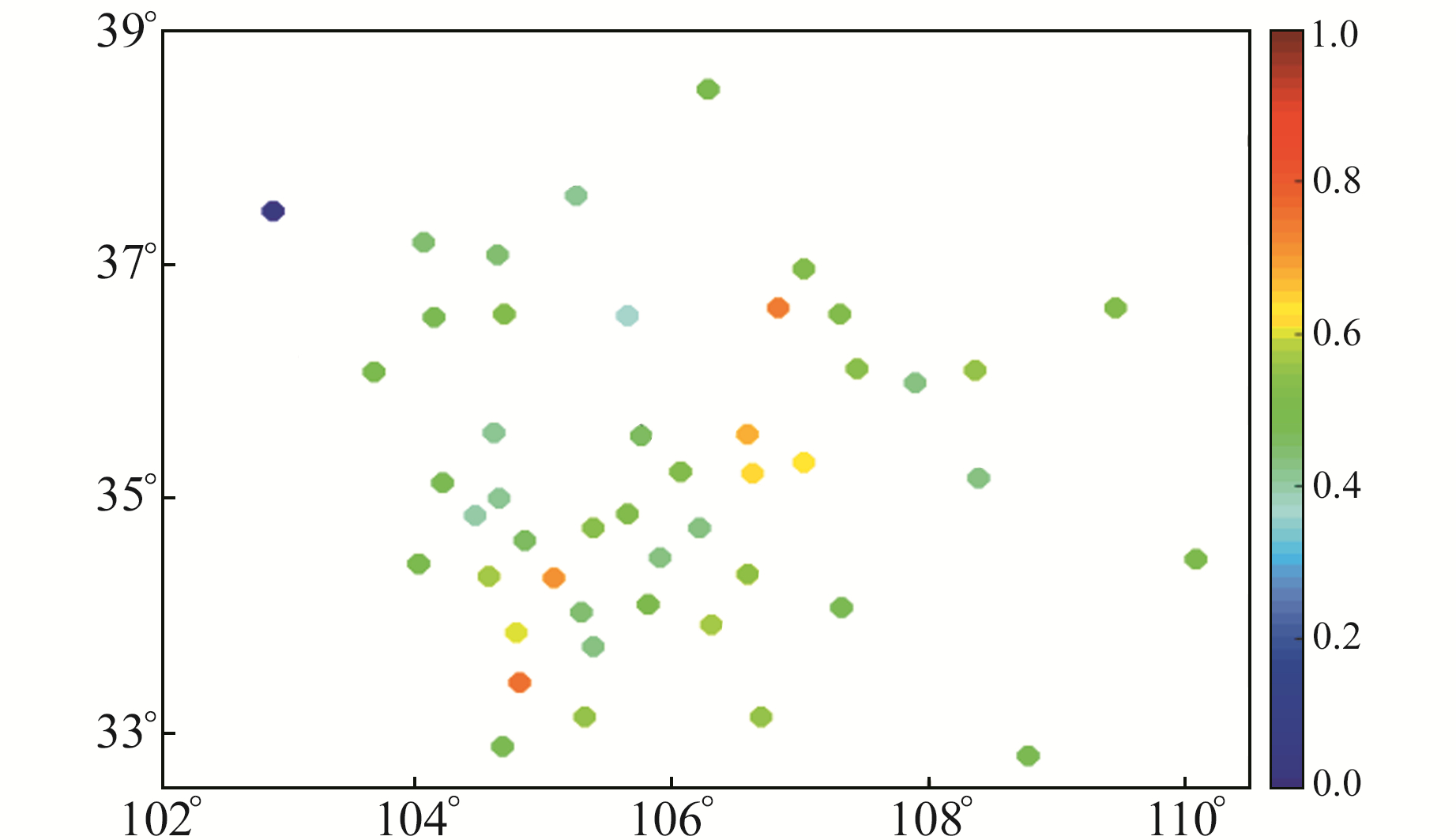
|
图 5 观测台站周年信号减少量 Fig. 5 Annual amplitude reduction of observation stations |
对GPS垂直位移和GRACE垂直形变时间序列的各项评价指标进行统计分析,部分台站观测数据存在以下问题:1)GSMQ站数据缺失较为严重,且存在多处明显阶跃;2)GSQS站存在多处明显阶跃,GSGL站GPS垂直位移季节信号异常,与研究区整体差异较大;3)LNMY和LNLH站GPS周年信号相位与研究区其他台站存在显著差异。在统计过程中对观测数据存在明显异常的台站进行简单剔除,其他43个台站的观测数据时间序列统计结果见表 2。
|
|
表 2 观测台站垂直位移时间序列统计结果 Tab. 2 Statistics of vertical displacement time series of observation stations |
以PLCX和QYXN站为例,根据表 2统计结果可知,2个台站GPS垂直位移和GRACE垂直形变时间序列的相关系数分别为0.80和0.85,结合图 1结果可知,2个台站GPS垂直位移和GRACE垂直形变时间序列变化的一致性较强。由表 2可知,PLCX和QYXN站GPS垂直位移的周年信号振幅值分别为5.8 mm和4.7 mm,GRACE垂直形变的周年信号振幅值分别为3.9 mm和3.6 mm,均方根误差减少量分别为0.37和0.46,周年信号减少量分别为0.64和0.74,经过GRACE负荷形变改正后,GPS垂直位移时间序列的周年信号明显减小。
由表 2可知,研究区内观测台站GPS垂直位移的周年信号振幅最大值为9.24 mm、最小值为4.05 mm、均值为6.00 mm;GRACE垂直形变的周年信号振幅最大值为4.98 mm、最小值为3.08 mm、均值为3.70 mm;GPS垂直位移和GRACE垂直形变时间序列相关系数的最大值为0.85、最小值为0.44、均值为0.72。扣除GRACE垂直形变后,GPS垂直位移均方根误差减少量的最大值为0.46、最小值为0.08、均值为0.29;GPS垂直位移周年信号减少量的最大值为0.75、最小值为0.37、均值为0.51。GRACE垂直形变能有效解释50%以上的GPS垂直位移周年信号,GPS垂直位移时间序列包含的非构造形变中约29%来源于由环境负载变化所引起的负荷形变。由于研究区处于中国内陆区域,非潮汐海洋变化对垂直形变影响极小,可忽略不计,且相关研究表明,该区域陆地水储量变化较小[19]。因此,研究区内GPS垂直位移可能主要由大气变化所引起,除环境负荷外,热膨胀效应及GPS数据处理造成的虚假信号等因素也是引起GPS垂直位移时间序列非线性变化的重要因素[18]。
结合图 3~5及表 2结果可知,研究区内台站垂直位移存在局部特征,在甘肃庆阳和平凉地区垂直位移与其他地区存在明显差异,相关系数、均方根减少量和周年信号减少量均高于其他地区,具体原因还需进一步研究分析。
3 结语本文基于中国大陆构造环境监测网络和CORS网在陕甘宁地区共48个连续观测台站数据,解算得到GPS垂直位移时间序列,并结合GRACE时变重力场Mascon模型解CSR RL05M数据计算得到垂直形变时间序列,从相关系数、均方根减少量和周年信号减少量等方面对陕甘宁地区地表垂直形变特征进行定量分析。结果表明:
1) 研究区内台站垂直形变存在局部特征,甘肃庆阳和平凉地区(35°~37°N,106.5°~108.5°E)垂直形变与其他地区存在明显差异,相关系数、均方根减少量和周年信号减少量均大于其他地区。
2) 观测台站GPS垂直位移和GRACE垂直形变时间序列相关系数最大值为0.85、最小值为0.44、均值为0.72;GPS垂直位移的周年信号振幅最大值为9.24 mm、最小值为4.05 mm、均值为6.00 mm;GRACE垂直形变的周年信号振幅最大值为4.98 mm、最小值为3.08 mm、均值为3.70 mm;GPS垂直位移周年信号减少量最大值为0.75、最小值为0.37、均值为0.51,均方根误差减少量最大值为0.46、最小值为0.08、均值为0.29。
3) 研究区内GPS垂直位移和GRACE垂直形变时间序列的一致性较强,GRACE垂直形变能有效解释50%以上的GPS垂直位移周年信号,GPS垂直位移时间序列包含的非构造形变中约29%来源于由环境负载变化引起的负荷形变。
致谢: 感谢原甘肃省测绘地理信息局提供甘肃省CORS网观测数据。
| [1] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Review of Geophysic and Space Physics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [2] |
姜卫平, 夏传义, 李昭, 等. 环境负载对区域GPS基准站时间序列的影响分析[J]. 测绘学报, 2014, 43(12): 1 217-1 223 (Jiang Weiping, Xia Chuanyi, Li Zhao, et al. Analysis of Environmental Loading Effects on Regional GPS Coordinate Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1 217-1 223)
(  0) 0) |
| [3] |
王林松, 陈超, 邹蓉, 等. 利用GPS与GRACE监测陆地水负荷导致的季节性水平形变:以喜马拉雅山地区为例[J]. 地球物理学报, 2014, 57(6): 1 792-1 804 (Wang Linsong, Chen Chao, Zou Rong, et al. Using GPS and GRACE to Detect Seasonal Horizontal Deformation Caused by Loading of Terrestrial Water:A Case Study in the Himalayas[J]. Chinese Journal of Geophysics, 2014, 57(6): 1 792-1 804)
(  0) 0) |
| [4] |
贾路路, 王阅兵, 连尉平, 等. "陆态网"GPS与GRACE的中国大陆地表垂直形变对比分析[J]. 测绘学报, 2018, 47(7): 899-906 (Jia Lulu, Wang Yuebing, Lian Weiping, et al. Comparison and Analysis of Crustal Vertical Deformation in Mainland China Observed by GPS from CMONOC and GRACE[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 899-906)
(  0) 0) |
| [5] |
Davis J L, Elósegui P, Mitrovica J X, et al. Climate-Driven Deformation of the Solid Earth from GRACE and GPS[J]. Geophysical Research Letters, 2004, 31(24)
(  0) 0) |
| [6] |
Fu Y N, Freymueller J T. Seasonal and Long-Term Vertical Deformation in the Nepal Himalaya Constrained by GPS and GRACE Measurement[J]. Journal of Geophysical Research, 2012, 117(B3)
(  0) 0) |
| [7] |
丁一航, 黄丁发, 师悦龄, 等. 利用GPS和GRACE分析四川地表垂向位移变化[J]. 地球物理学报, 2018, 61(12): 4 777-4 788 (Ding Yihang, Huang Dingfa, Shi Yueling, et al. Determination of Vertical Surface Displacements in Sichuan Using GPS and GRACE Measurements[J]. Chinese Journal of Geophysics, 2018, 61(12): 4 777-4 788)
(  0) 0) |
| [8] |
魏娜, 施闯, 刘经南. 基于GPS和GRACE数据的三维地表形变的比较及地球物理解释[J]. 地球物理学报, 2015, 58(9): 3 080-3 088 (Wei Na, Shi Chuang, Liu Jingnan. Annual Variations of 3-D Surface Displacements Observed by GPS and GRACE Data: A Comparison and Explanation[J]. Chinese Journal of Geophysics, 2015, 58(9): 3 080-3 088)
(  0) 0) |
| [9] |
van Dam T, Wahr J, Lavallee D. A Comparison of Annual Vertical Crustal Displacements from GPS and GRACE over Europe[J]. Journal of Geophysical Research, 2007, 112(B3)
(  0) 0) |
| [10] |
Tregoing P, Watson C, Ranmillien G, et al. Detecting Hydrologic Deformation Using GRACE and GPS[J]. Geophysics Research Letters, 2009, 36(15)
(  0) 0) |
| [11] |
崔阳, 吕志平, 李林阳, 等. GNSS大网双差模型并行快速解算方法[J]. 测绘学报, 2017, 46(7): 848-856 (Cui Yang, Lü Zhiping, Li Linyang, et al. A Fast Parallel Processing Strategy of Double Difference Model for GNSS Huge Networks[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 848-856)
(  0) 0) |
| [12] |
沈迎春, 闫昊明, 彭鹏, 等. 质量负荷引起地表形变的格林函数和球谐函数方法对比研究[J]. 武汉大学学报:信息科学版, 2017, 42(7): 1 008-1 014 (Shen Yingchun, Yan Haoming, Peng Peng, et al. Comparative Study of Green's Function and Spherical Harmonic Function Methods on Surface Deformation Caused by Mass Loading[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 1 008-1 014)
(  0) 0) |
| [13] |
李英冰.固体地球的环境变化响应[D].武汉: 武汉大学, 2003 (Li Yingbing.Solid Earth Response to Environmental Variation[D].Wuhan: Wuhan University, 2003) http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031873.htm
(  0) 0) |
| [14] |
CSR GRACE Mascons Solutions[EB/OL]. http://www2.csr.utexas.edu/grace/RL05_mascons.html, 2019
(  0) 0) |
| [15] |
Flechtner F, Dobslaw H, Fagiolini E.AOD1B Product Description Document for Product Release05(Rev.4.2)[R].GFZ German Research Centre for Geosciences, 2014
(  0) 0) |
| [16] |
陈超, 邹蓉, 刘任莉. 联合GPS和GRACE研究青藏高原南部地区垂直形变的季节性波动[J]. 武汉大学学报:信息科学版, 2018, 43(5): 669-675 (Chen Chao, Zou Rong, Liu Renli. Vertical Deformation of Seasonal Hydrological Loading in Southern Tibet Detected by Joint Analysis of GPS and GRACE[J]. Geomatics and Information Science of Wuhan University, 2018, 43(5): 669-675)
(  0) 0) |
| [17] |
李伟伟.全球与区域地壳形变的多源数据序列处理与信号分析[D].上海: 同济大学, 2017 (Li Weiwei.Data Processing and Signal Analysis for Multi-Data Series of Crustal Deformation on Global and Regional Scales[D].Shanghai: Tongji University, 2017) http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201712015.htm
(  0) 0) |
| [18] |
谷延超.顾及先验信息的时变重力场模型信号提取及其负荷形变应用[D].成都: 西南交通大学, 2018 (Gu Yanchao.Extracting Mass Variations from GRACE Time-Varied Gravity Models with Priori Information Constraints and Its Application on Loading Deformation[D].Chengdu: Southwest Jiaotong University, 2018)
(  0) 0) |
| [19] |
谢小伟, 许才军, 龚正, 等. 利用GRACE反演陕甘晋高原地下水储量变化[J]. 测绘通报, 2018(1): 133-137 (Xie Xiaowei, Xu Caijun, Gong Zheng, et al. Groundwater Storage Changes in Shan-Gan-Jin Plateau Derived from GRACE[J]. Bulletin of Surveying and Mapping, 2018(1): 133-137)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Middle-Yanta Road, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, 1 Middle-Yanta Road, Xi'an 710054, China;
4. School of Civil Engineering and Geomatics, Southwest Petroleum University, 8 Xindu Road, Chengdu 610500, China;
5. Army Logistics University of PLA, 20 Beiyi Road, Chongqing 401311, China
 2020, Vol. 40
2020, Vol. 40

