文章信息
- 王志远, 邢志国, 王海斗, 单德彬
- WANG Zhi-yuan, XING Zhi-guo, WANG Hai-dou, SHAN De-bin
- 非金属夹杂物特性对钢铁材料疲劳性能影响的研究进展
- Research progress in influence of non-metallic inclusion characteristics on fatigue properties of iron and steel materials
- 材料工程, 2020, 48(5): 1-12
- Journal of Materials Engineering, 2020, 48(5): 1-12.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000266
-
文章历史
- 收稿日期: 2019-03-25
- 修订日期: 2019-12-06
2. 陆军装甲兵学院 装备再制造技术国防科技重点实验室, 北京 100072
2. National Key Laboratory for Remanufacturing, Academy of Army Armored Forces, Beijing 100072, China
随着国民经济的蓬勃发展,应用于大型冶金机械、矿山机械、装甲车辆、船舶、交通运输等行业中的重载机械装置也得到了长足稳定的发展[1]。为满足重点工程项目的顺利进行,研究人员对大型重载零件使用寿命提出更高的要求,高承载能力、高可靠性、高抗疲劳性成为零件的主要评估指标。在实际工况下重载零件失效的原因多为疲劳损伤, 而零件中对疲劳性能影响最大的因素就是钢材中含有的非金属夹杂物,几乎所有的疲劳裂纹源都是在钢材中的非金属夹杂物周围开始萌生的[2]。如何有效地抑制钢材中非金属夹杂物对疲劳性能的影响一直是一项技术难题。国内外研究学者针对这一难题进行了大量的研究[3-5],这些研究多集中于如何减少钢材夹杂物的含量、缩小夹杂物尺寸、降低钢材夹杂物与基体间的不良作用等方面,总结出许多半定量乃至全定量相关数学模型去测试非金属夹杂物对钢材疲劳寿命的影响,精准而高效的数学预测模型可以指导钢材冶炼,进而提供更加科学的方法去合理控制夹杂物含量。
基于此,本文总结了目前国内外重载零件钢材中非金属夹杂物对疲劳性能影响的主要数学模型,以期从科学的角度为工程机械中的重载零件制造提供参考依据,提高重载零件的服役安全性。
1 夹杂物特征提取重载零件钢材的检测分析技术是研究钢中非金属夹杂物对钢材疲劳性能影响的第一个环节,也是最重要的环节,只有精准全面地对钢材中非金属夹杂物的存在形式以及夹杂物的各项性能参数进行评估,才能清楚地了解非金属夹杂物的来源和生成机制,从而根据非金属夹杂物对疲劳性能的影响有针对性地提出数学模型进行验证。
1.1 钢材中非金属夹杂物的实验检测分析方法非金属夹杂物的特征信息提取的方法多种多样,随着实验手段越来越先进,非金属夹杂物的检测从二维平面分析到三维取样分析,其检测分析方法也越来越多,而在试样测试体积、获得的信息类型、分析时间长短各有优缺点,本节通过介绍钢材中非金属夹杂物的实验分析方法,准确获取夹杂物信息,并为后续的疲劳模型建立创造有利条件。
在以往的研究中有许多可以检测钢材中夹杂物的方法,如二维平面分析中的金相图谱评级[6]、ASPEX Explorer[7]大面积自动扫描电镜检测、硫印法[8]等;无损检测方法中的超声波检测[9]、电磁法、Micro-CT法[10]等;夹杂物浓缩及萃取方法中的大样电解[11]、电子束重熔、冷坩埚重熔法等[12]。上述方法中,光学金相分析可以分析微小尺寸夹杂物,并根据配备的能谱分析有效给出夹杂物的含量,但是很难用于大体积钢材的检测;无损检测法可以用于检测大体积钢材,但小于100 μm的夹杂物很难发现;夹杂物集中萃取的方法可以无偏差地分析大体积钢材中夹杂物的状态,其中大样电解法是最常规的检测手段,其原理如图 1(a)所示,测试结果如图 1(b), (c)所示,该方法可以完整保留夹杂物形态信息,并能准确地判定其尺寸及成分,但是耗时且价格昂贵[13]。

|
图 1 电解萃取法检测夹杂物[10-11] (a)夹杂物电解装置示意图;(b)电解法获取的夹杂物典型形貌示意图;(c)球状夹杂物3D重现图 Fig. 1 Detection of inclusion size by electrolytic extraction method[10-11] a)schematic diagram of inclusion electrolysis device; (b)schematic diagram of typical morphology of inclusions obtained by electrolysis; (c)3D reproduction diagram of spherical inclusion |
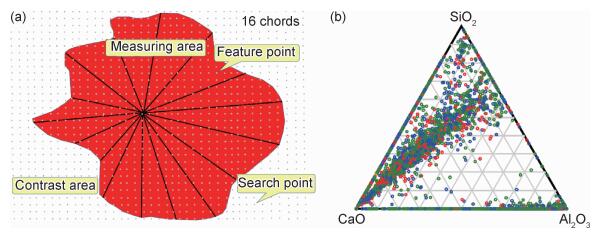
目前最高效的测试方法就是利用ASPEX Explorer[7]夹杂物自动分析电镜系统,如图 2(a)所示,采用16旋转弦算法对大面积范围内的平面和粒子进行形状参数分析与元素含量判定,其结果如图 2(b)所示,可以测量一定范围内夹杂物的数量、含量、尺寸信息等关键因素。
夹杂物检测的方法纷繁复杂,但归根结底都是为了更好地统计钢材中夹杂物的存在状态及夹杂物的尺寸信息。在夹杂物尺寸统计研究中,Murakami和Endo[14]于1994年提出一个夹杂物面积的计算模型,该模型利用统计极值法估测出钢中最大夹杂物尺寸。
首先定义参量S0为钢材镜面中的一个标准测试面积,通过金相显微镜统计标准测试面积中的夹杂物尺寸,可以观察到在标准测试面积中夹杂物的最大粒度呈极值分布,Murakami认为钢中夹杂物服从的函数分布为Gumbel函数中的第1类近似函数,其表达式如式(1)所示:
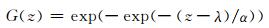
|
(1) |
式中:G(z)为最大值累计概率密度;α为尺寸参数,表示分布的分散程度;λ为位置参数,表示概率密度最大处的夹杂物粒度。设N为统计的样本量,利用线性回归方程拟合N个样本量中夹杂物最大尺寸与样本量之间的关系,设i为总体样本中最大粒径度由小到大排列后对应的顺序号,则试样总表面中最大的粒径即为第i个S0面积中的夹杂物尺寸Xi。
Shi等[15]于1999年提出广义Pareto分布法测量钢中的最大夹杂物尺寸,广义Pareto分布法通过预设3个参数,门槛值u、形状参数ζ、比例参数σ,则大于门槛值u的夹杂物尺寸的概率函数F(x)符合广义Pareto分布,其表达式如式(2)所示:
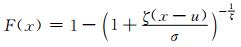
|
(2) |
该方法最重要的步骤就是选取门槛值以及相关的形状参数ζ、比例参数σ以及实验中所需的钢材数量N。英国谢菲尔德大学的Atkinson课题组[16]设计程序利用广义Pareto分布法计算钢材的体积效应与夹杂物最大尺寸的关系。程序采用Monte Carlo法对样本进行随机扩增,通过最大似然估计迭代出夹杂物尺寸参数,似然函数的取值区间即为最大夹杂物的特征尺寸的取值范围。
应用上述两种方法可以有效地统计出夹杂物的尺寸参数信息,随后需要进行大量的疲劳实验来探究钢材疲劳强度与非金属夹杂物尺寸的关系,并给出相关的数学模型[17]。通过文献总结[18-20],夹杂物与钢材疲劳性能的数学模型发展可以分为3个阶段:(1)根据大量实验数据总结经验公式,形成最基本的数学模型。(2)将夹杂物的各项性能指标作为基本参数进行模型的修正。(3)利用断裂力学及验证性实验对修正后的数学模型进行有效的验证。
2 夹杂物与钢材疲劳性能经典模型的建立本节主要介绍5种定量分析非金属夹杂物与疲劳性能的数学模型,这5种模型分别从不同的疲劳损伤原理进行探究。
2.1 Frost模型Frost模型[21]从夹杂物对疲劳裂纹的影响进行分析,认为夹杂物的尺寸效应直接导致钢材中的疲劳裂纹萌生,并以裂纹扩展公式作为研究的理论基础,进行公式的优化和扩展。Frost模型及其相似的数学模型的经验公式为
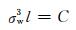
|
(3) |
式中:σw3为疲劳极限;l为裂纹长度;C为材料性能参数。该模型主要是预测夹杂物引起小裂纹之后的疲劳性能变化,模型的创建思路受到断裂力学以及实验的修正,可以精准预测出材料的疲劳性能。在后续的研究工作中,Kobayashi和Nakazawa等[22]对模型进行了研究并根据缺陷长度参数修正了系数,该参数在3~4之间,主要是根据夹杂物造成的裂纹大小作为出发点,即设置小裂纹长度适用范围,如式(4)所示。
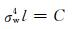
|
(4) |
Li等[23]根据缺陷的尺寸作为参考因素设置缺陷中的最小圆直径D作为系数去修正疲劳极限σw的经验公式,并引入常数K来平衡夹杂物形状引起的变化,σw0为材料的无缺口光滑试样的疲劳极限, 如式(5)所示:
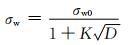
|
(5) |
该等式借鉴断裂力学中压应力与疲劳强度之间的关系,进一步将受力大小这一参数引入夹杂物对疲劳性能影响的数学模型。但是由于条件限制,夹杂物无法有效设置大小而没有考虑应力场强度因子对最终性能的影响,Peterson[24]在后续的研究过程中引入应力集中系数K′、夹杂物几何尖端半径P和材料常数C′作为外加参数修正了Frost模型,如式(6)所示:
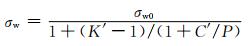
|
(6) |
该模型针对非金属夹杂物具有各种不规则的形状这一因素,进行了参数修正,但是夹杂物的形状参数K′只能应用于计算球体或者椭球形夹杂物等形状简单的夹杂物。
2.2 Kitagawa和Takahashi模型Kitagawa和Takahashi模型[25]创新性地将夹杂物影响裂纹扩展的数值进行定量化分析,并提出疲劳裂纹扩展门槛值作为研究的重点,同时进行修正研究,这一概念的提出使得钢材冶炼过程中不再盲目地追求细化夹杂物尺寸,为实际生产带来了诸多益处。Kitagawa和Takahashi模型及其相似的数学模型的经验公式为:
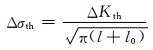
|
(7) |
该模型定性又定量地在夹杂物与疲劳数据模型中引入了疲劳阈值Δσth的概念,其中l为材料中小裂纹长度,l0为计算得出的临界裂纹长度增加量,即在小于l+l0参数下,金属将不会产生疲劳失效行为。在模型中的解释为断裂因子ΔKth与小裂纹尺寸成正比,但会存在一个极限值,使得钢材即使具有小于该尺寸的夹杂物也不会产生疲劳失效行为。但是该等式没有明确地给出计算ΔKth的相关函数。
Smith[26]在随后的研究中根据Kitagawa和Takahashi模型精确地给出了临界裂纹长度增加量l0的计算方法,研究中近似认为ΔKth和Δσw0可以拟合出两条直线,如式(8)所示,这两条直线包含了疲劳实验点数据,并认为实际试样中的裂纹长度高于预测出的l0即失效。虽然这一预测的误差很大,但是却定义出了夹杂物的临界尺寸,该参数为传统的夹杂物研究提供了新的方向,即钢中的夹杂物尺寸越小,它对疲劳性能的影响就越小,但是无限地追求夹杂物的细化,就会大幅度地提高钢材的生产成本,因此只要把夹杂物控制在某一临界尺寸以下,疲劳裂纹就不会从夹杂物处萌生。
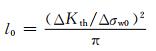
|
(8) |
Haddad等[27]根据Smith测试的方法,将l0进一步代入疲劳极限拟合公式中,准确测试出试样中存在的缺陷阈值与试样疲劳极限的关系,其表达式为:
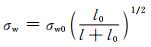
|
(9) |
这种参数的设置有利于从材料参数σw0与断裂因子ΔKth的角度采用常规的断裂力学去评估夹杂物对钢材疲劳性能的影响。
Tanaka等[28]根据式(9)的思路,通过设置与材料晶体结构相关的阈值参数对疲劳极限进行预测,其模型假设在设置阈值以上疲劳过程首先由夹杂物及裂纹尖端位错滑移带引起的,并在扩展到晶界的时候出现阻碍作用,从而影响周围的晶粒状态产生失效,表达式如式(10)所示。
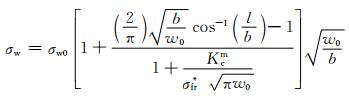
|
(10) |
式中:σfr*为位错运动中的摩擦力;Kcm为微观应力场强度因子的阈值;b为裂纹长度参数;w0为试样的晶粒尺寸。该模型从二维角度出发对Kitagawa和Takahashi模型进行参数修正,但是其原理可以应用到三维结构中来分析三维夹杂物对钢材疲劳性能的影响。
2.3 Murakami和Endo模型Murakami和Endo模型[14]将夹杂物面积和基体硬度值作为研究的重点,并且量化夹杂物面积尺寸,使得夹杂物在钢材中形成面积尺寸的评判标准,并进行大量的实验验证。Murakami和Endo模型及其相似的数学模型的经验公式为
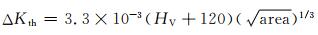
|
(11) |
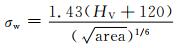
|
(12) |
式中:ΔKth为应力场强度因子;HV为基体的维氏硬度;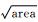
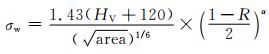
|
(13) |
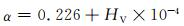
|
(14) |
Murakami和Endo提出的模型不需要采用疲劳测试验证就可以达到较高的预测精度,该模型是以Frost模型为计算依据,加入基体的维氏硬度HV、夹杂物或者缺陷面积的平方根 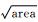
Usami和Shida模型[30]针对钢材中夹杂物的分布,设定弹性区域与塑性区域,并根据不同的塑性与弹性形变作为疲劳破坏的出发点,从另一个角度解释钢材在疲劳过程中发生断裂的本质。Usami和Shida模型及其相似的数学模型的经验公式为
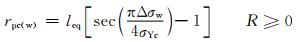
|
(15) |
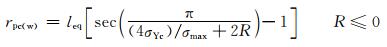
|
(16) |
式中:Δσw为疲劳实验所设置的应力级;σmax为疲劳极限下对应的最大应力;leq为二维平面下裂纹的等效长度的1/2。该模型设置了塑性区应力场强度因子rpc(w)和循环应力σYc,以夹杂物的尖端塑性区大小及钢材所受应力大小为出发点,总结出经验公式。该模型可以较好地应用在不同受力环境下工作的钢材,并为钢材的性能检测提供了数学依据。
2.5 Abdel-Raouf模型Abdel-Raouf模型[31]从晶体结构角度出发,认为夹杂物是存在于钢材晶体中的不确定因素,并根据夹杂物的特征信息设定夹杂物的损害值,从微观的角度揭示钢材的疲劳失效问题。Abdel-Raouf模型及其相似的数学模型的经验公式为
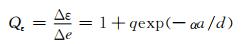
|
(17) |
式中:Δε为夹杂物局部应变范围;Δe为标准应变;d为裂纹扩展方向的平均晶粒尺寸;α为位错滑移修正参数;q为典型的晶体常数。该模型以夹杂物等缺陷引起的裂纹闭合效应作为公式推导依据,拟合疲劳裂纹的发展过程,随后通过有效的数学手段可以计算出疲劳极限的数值,并与大量的实验验证结果相吻合。
3 根据夹杂物特性对疲劳数学模型的修正疲劳损伤是钢铁材料在循环载荷作用下的破坏现象,该现象起因主要为钢铁材料中夹杂物自身的性能参数与基体材料不符合,成为异质相,在受到循环应力作用时成为破坏源,最终导致整个材料失效[32]。因此,若想定量地给出夹杂物与疲劳的关系式,还要考虑夹杂物与基体间的多种性能参数匹配的问题。本章将着重以夹杂物的外在形貌参数、力学参数以及与基体的协同作用为出发点,进行综合分析。
3.1 夹杂物形貌参数对疲劳性能的影响钢中的非金属夹杂物对疲劳性能的影响早已引起科研人员的广泛关注[33]。在重载零件钢材中,非金属夹杂物最直观的影响,就是由于形貌特征所带来的有害影响。其中,以夹杂物的尺寸效应影响最大,研究人员根据夹杂物尺寸特征已经开展了一系列的研究工作,发展至今,已通过量化夹杂物尺寸的门槛值来判断钢材失效是否由夹杂物引起[34]。其次就是夹杂物的曲率半径对钢材失效的影响,曲率半径越小,夹杂物的形状越偏向于角形,而角形结构引起的应力集中十分严重,疲劳性能也随之下降。本节主要从钢材中夹杂物的大小、形状以及夹杂物的表面粗糙度为出发点,分析夹杂物形貌参数对钢材疲劳性能的影响,并根据相关文献总结出定量分析的数学模型。
Murakami等[35]结合疲劳强度因子、维氏硬度将夹杂物尺寸作为参数,构建了预测高强度钢的疲劳强度的数学模型,定量化分析夹杂物尺寸对钢材疲劳性能的影响。Wang等[36]按照Murakami模型的思路,将疲劳寿命这一参数引入公式中,对42CrMo4, 54SC6, 55SC7, 60CV2等多种高强钢进行有效的拟合,其数学模型为:
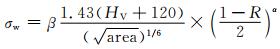
|
(18) |
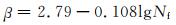
|
(19) |
Akiniwa等[37]将断裂力学中相关的裂纹扩展计算引入Murakami模型中,以Paris公式作为计算依据,对夹杂物尺寸因素影响钢材疲劳性能的数学模型进行修正,其表达式为:
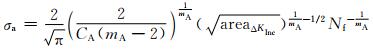
|
(20) |
式中:CA和mA为材料参数;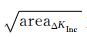
Liu等[38]从Basquin方程拟合S-N曲线的角度出发,对Murakami模型进行扩展,其模型表达式为:
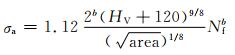
|
(21) |
该模型将Basquin方程引入模型中,可以有效地预测出在不同循环周次下,夹杂物与疲劳寿命之间的关系,经过实验验证,发现疲劳寿命在106~109循环周次下测试效果最准,可以根据夹杂物尺寸精确地给出钢材的疲劳极限。
对于非金属夹杂物的形状而言,在钢材基体中多以不变形球状夹杂物、大尺寸细长条状夹杂物、簇群状、不规则多边形形状夹杂物居多,这些形状夹杂物都可能成为疲劳裂纹源。因此,夹杂物形状对疲劳性能的影响亟待完善。在以往的研究中,Murakami等[14]根据实验定性地给出夹杂物形状对疲劳性能的影响。其统计结果如表 1所示[39-42]。
| Inclusionsize/μm2 | Shape ofinclusion | Nominal stressat inclusion/MPa | Fatiguelimit/MPa |
| 577 |  |
954 | 806 |
| 254 |  |
995 | 863 |
| 234 |  |
973 | 870 |
| 99 |  |
963 | 934 |
| 156 | 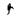 |
978 | 899 |
| 346 | 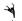 |
1001 | 841 |
| 491 | 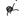 |
1023 | 817 |
| 804 | 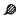 |
1003 | 784 |
| 836 | 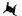 |
960 | 782 |
由表 1可知,引起上述材料疲劳失效的夹杂物形状没有统一的标准,但从定性角度分析,可以看出夹杂物的形状越不规则,其曲率半径值越小,钢材的疲劳性能越差。但是由于夹杂物在基体中的存在形式过于复杂,很难对其他影响因素进行控制,进而给出半定量的数学模型去进一步揭示夹杂物形状参数对其疲劳性能的影响。
因此,Gillner等[43]借助模拟的手段探究夹杂物形状因素对疲劳性能的影响,提出一种新的数学模型用来计算夹杂物对疲劳性能的影响。该模型由统计学组成,预设多个代表性体积单元计算出的晶体塑性本构模型。其表达式为:
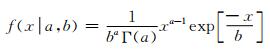
|
(22) |
式中:a为形状参数;b为速率参数;Γ(a)为利用Gamma函数分布将晶粒的尺寸及纵横比进行拟合的方程表达式[44]。一个模拟单元代表一个晶粒,其中包括尺寸、形状、表面粗糙度等相关参数,随后设置异质相也就是夹杂物的参数。每一个夹杂物与晶粒做比较,可以表征100多种夹杂物,它们在统计学上具有相同的微观结构特性,但是细节上还是有差异的。随后对模拟单元进行相同的应力振幅及加载速率的循环载荷疲劳测试,研究预设的夹杂物单元在基体中的损伤形式,通过对比分析可得:夹杂物形状参数中尺寸参数对基体疲劳性能影响程度最大,第二为夹杂物的表面粗糙度,第三为夹杂物的曲率半径。
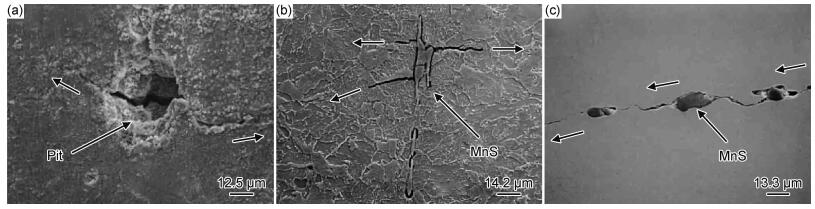
3.2 夹杂物的化学元素组成 3.2.1 硫化物对基体的影响硫在钢中通常以硫化锰(MnS)的形式存在[45]。其硬度较低,弹性模量、热膨胀系数、塑性、热物性等物理性能与基体匹配较好。硫化物容易随着钢材基体而产生形变,沿着钢材加工方向变长,导致夹杂物所在的区域存在显著差异,如图 3(a), (b)所示[46],图 3(a)中随着硫化物脱落形成了圆形脱落坑,图 3(b), (c)为团簇状硫化物引起疲劳失效及其裂纹扩展方向。硫化物同时也改变了夹杂物在基体中的受应力方向,从而影响每个方向上的夹杂物结构特征;硫化物通常以团簇形式存在于钢材基体中,团簇状夹杂物之间,由于位置协调作用容易出现应力集中点,从而形成裂纹源, 如图 3(c)所示,大幅度降低了钢材基体的韧性和延展性;硫的存在也改善了材料的切削性能[47-48]。
Cyril等[49]在研究中采用不同的冶炼技术炼制多种不同硫含量的SAE4140钢材(高硫:0.077%,低硫:0.012%,超低硫:0.004%,质量分数),并根据Roessle和Fatemi[50]提出的数学模型,引入硫含量这一参数,从定量的角度分析了硫化物在钢材中的含量对钢材疲劳性能的影响,其表达式如式(23)所示:
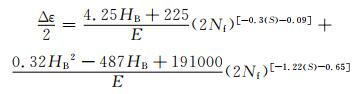
|
(23) |
式中:HB为基体硬度;E为基体的弹性模量;S为钢材的含硫量;Δε为应力幅值;Nf为疲劳循环载荷。根据模型拟合出疲劳寿命曲线,对不同硫含量的材料和两种硬度水平的试样进行寿命预测,寿命预测曲线在102~106循环周次之间。
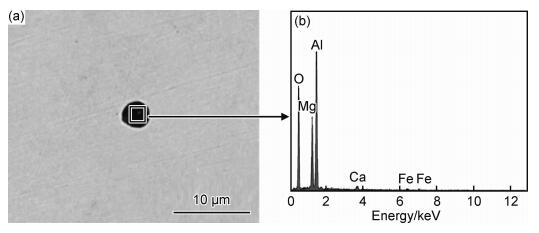
3.2.2 含Al夹杂物含Al夹杂物是钢材中最常见的夹杂物,在钢材中有多种存在形式,图 4(a)所示为钢材中含Al元素夹杂物显微形貌,图 4(b)为能谱分析结果,这类夹杂物主要为钙铝酸盐和Al2O3,钙铝酸盐在钢材基体中属于不变形且具有坚硬结构的夹杂物,多为零部件服役过程中的重要疲劳裂纹源[51]。因此,在钢材制造中,必须控制夹杂物为CaO-SiO2-Al2O3系中的钙斜长石、磷石英以及假硅灰石相邻的低熔点区塑性夹杂物[52]。Al2O3夹杂物多来自钢材冶炼中,加入铝脱氧后,钢液中分离出来的Al2O3颗粒没有来得及释放而残留于基体中。由于铝具备较强的亲氧能力,是一种高效的脱氧剂,而残留的Al2O3夹杂物,很难形成低熔点的塑性夹杂物,在后续的轧制过程中,流动趋势相对迟缓,造成组织不均匀,对钢材性能影响较大,在后续的疲劳过程中会成为主要的裂纹源[53]。
Al2O3夹杂物又会与冶炼过程中加入MgO基的耐火材料形成尖晶石结构的MgO·Al2O3。尖晶石结构的夹杂物对于钢材更是非常有害的杂质,在目前的研究中,尖晶石结构的MgO·Al2O3大多以改性的液态钙铝酸盐形式存在[54]。
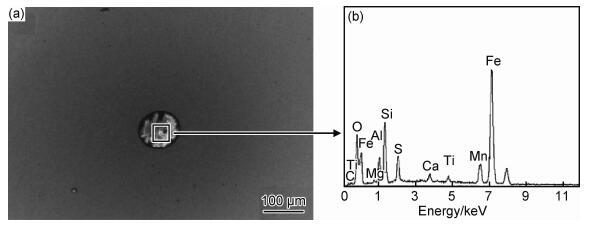
3.2.3 硅化物对疲劳性能的影响Si元素形成的夹杂物在钢材基体中多以铁硅酸盐(2Fe·SiO2)以及锰硅酸盐(2MnO·SiO2)的形式存在,图 5(a)所示为钢材中含Si元素夹杂物显微形貌,图 5(b)为能谱分析结果。该类型夹杂物主要为球状玻璃质,任意分布在钢材基体中,硅酸盐夹杂物主要以SiO2为主,熔点低,塑性强,会在钢材后续轧制过程中延展或破碎变小,且容易随着基体的变化而产生形变,并向两边延伸出裂纹,在钢材疲劳过程中容易形成裂纹源,最终造成疲劳失效[55]。
Si夹杂物因其优异的延展性、韧性以及与基体协同变形的能力在多种复合材料中充当强化相,如利用SiC增强的铝合金、改性铸造合金等,都是将Si元素作为强化相后使得基体性能提高。但是含Si增强相复合材料的疲劳裂纹扩展行为很大程度上取决于增强相的体积分数、尺寸以及与基体的微观结构等,由于增强相在基体中数量较多,周围基体环境过于复杂,其性能与疲劳之间关系的数学模型到目前为止研究得还不够充分,大多借助于有限元模拟进行疲劳行为探究[56]。
3.3 夹杂物与基体的协同作用夹杂物对于高性能钢材来说,除了夹杂物自身的特征参数对疲劳性能具有较大的影响以外,夹杂物与基体之间的相互作用,夹杂物所处的周围基体环境等都会对疲劳性能产生很大的影响[57]。例如:夹杂物在基体中的位置、夹杂物与基体黏滞力,夹杂物在基体中受力方向以及夹杂物与基体的塑性差等。
高强钢疲劳失效过程中,夹杂物与钢材基体相互作用,裂纹会优先在夹杂物附近应力集中处萌生,并根据夹杂物与基体间相互作用的趋势,形成3个特征性区域,分别为光学暗区(optically dark area, ODA)、颗粒状亮光区(granular bright facet, GBF)、细颗粒区(fine granular area, FGA)[58]。
光学暗区(ODA)因处于夹杂物周围形成的粗糙区域上,在光学扫描镜下看起来颜色较浅而得名,ODA区域主要有3个明显的特征[59]:
(1) ODA区域由凹凸不平的团组成,凹凸的特征与马氏体结构相类似,但是比马氏体更小且亮度更低。
(2) 钢材的断裂区域上凹凸点配合较为精确,在连续循环载荷盈利下,凹凸结构会更加清晰,不同的应力比也会影响凹凸形貌配合的程度。
(3) 疲劳寿命越久,ODA区域就越清晰可见,一般在106循环周次之后就可以发现ODA区域,经过107循环周次后,ODA的凹凸形貌十分清晰。
目前有些研究认为光学暗区的形成主要是由于夹杂物中包含氢元素,氢元素在承受循坏载荷之后,会引起氢脆断裂,最终导致疲劳失效,影响传统的疲劳极限预测[60]。详细的机理还须进一步验证。目前最新的研究机制[54]认为疲劳断口中的ODA区域不是在裂纹扩展过程中形成的,而是由于循环载荷长期作用反复挤压产生的,夹杂物只是提供了ODA区域的位置,ODA区域大小更多与疲劳加载过程相关。
ODA区域与钢材疲劳性能之间关系紧密,与之相关的数学模型也层出不穷,本节主要介绍应用较为广泛的两类模型,其他模型多为在这两类模型基础上根据自身使用的钢材推导出来的优化模型。Murakami[61]依据钢材硬度与S-N曲线计算模型提出了ODA区域大小与钢材疲劳极限函数关系,如式(24)所示:
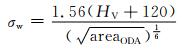
|
(24) |
Furuya等[62]根据Paris公式中断裂因子的计算,提出一套基于断裂因子疲劳寿命与ODA区域面积的计算模型,其函数关系式为:
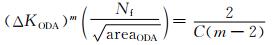
|
(25) |
颗粒状亮光区(GBF)区域出现在裂纹萌生的早期,是钢材由于内部裂纹萌生形成的固有特征,该区域比例对钢材疲劳寿命有着重要的影响[63]。GBF区远离试样边缘,在材料内部产生,周围会形成标准的“鱼眼”形貌,GBF区位于“鱼眼”中间,多数为非金属夹杂物诱导产生,其形成机制主要有以下3种原因:(1)氢元素导致裂纹萌生后产生的GBF区域;(2)球形碳化物脱落后产生;(3)基体细颗粒组织的失效[64-65]。
经过多年的理论探索与实验验证,GBF区域面积与钢材疲劳寿命的数学模型也发展得较为成熟,在众多模型中基于Murakami[61]建立的硬度与疲劳寿命的公式最为经典,Liu等[66]根据裂纹影响因子,建立了含有GBF区域参数的数学模型,该模型以Murakami模型为基础,并经过实验验证,拟合效果良好,其关系式为:
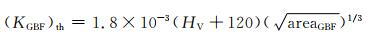
|
(26) |
Zhao等[67]设置GBF区域的尺寸与外加应力幅值σa为数学模型的初始参量,对下贝氏体和板条马氏体组成的高强度钢进行了疲劳寿命拟合,其表达式为:
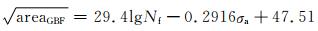
|
(27) |
Yang等[68]根据GBF区域大小与疲劳加载应力比rGBF探索出新型数学模型来估计钢材的疲劳强度,值得一提的是,该模型将氢气浓度CH也设置为主要变量,并用数学公式拟合,其表达式为:
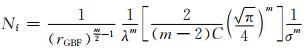
|
(28) |
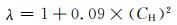
|
(29) |
细颗粒区(FGA)在扫描电子显微镜下属于灰度相对较小的亮区,部分也被称作颗粒状亮区。FGA区域的形成对应于钢材疲劳裂纹萌生期,其形成机理也是众说纷纭,Murakami等[69]提出由夹杂物对周围氢元素的捕获机制导致FGA的发生。Shiozawa等[70]则认为FGA是由分离的球形碳化物和基体之间界面处的裂纹聚结产生的。Sakai等[71]认为FGA的形成是细颗粒层剥离的结果;Grad等[72]认为钢材中晶粒细化是造成FGA产生的原因,并给出了预测寿命的计算模型;Nakamura等[73]在研究中通过在钢材上施加循环压应力并在预制小裂纹处得到与FGA类似的区域形貌;Li等[74]认为这只是局部产生FGA区域的方法,可能与晶体受疲劳载荷后二次结晶相关;Abdesselam等[75]认为FGA区域的尖端塑性区与板条状马氏体相似,其形成机理可能与钢材中马氏体含量相关。Spriestersbach等[76]认为FGA区域的形成多发生在真空环境服役下的表面有人工激光缺陷的样品上。因此,真空条件可能是FGA形成和产生的关键因素。
上述的FGA形成机制都认为FGA区域的形成是由于原始裂纹表面之间存在大量的循环压力,与裂纹闭合以及残余应力释放有关,由于钢材局部的强塑性变形,导致微观结构破碎并形成部分由纳米颗粒组成的FGA结构。针对这一机理进行相应的疲劳寿命预测数学模型探究,FGA与GBF的模型基础大致相同,都是在Murakami等建立的疲劳断裂阈值设计模型与Tanaka和Akiniwa等根据Paris公式设计的疲劳强度模型基础上发展的。最新的数学模型为Nehila等[77]根据FGA区域的长和宽作为参数,通过金属基体的堆垛层错能和位错滑移机制提出的疲劳寿命预测公式为:
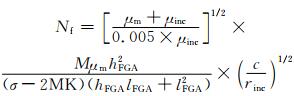
|
(30) |
式中:μm为基体的弹性模量;μinc为夹杂物的弹性模量;M为泰勒系数;σ为屈服强度;MK和c分别为堆垛层错能和位错滑移机制修正系数;rinc为疲劳加载应力比;hFGA为FGA区域高度;lFGA为FGA区域长度。该公式从金属微观结构组成的角度揭示了FGA区域形成的机理,具有一定的创新性。
4 结束语非金属夹杂物对重载零件钢材的疲劳性能有着较大的影响,本文从非金属夹杂物的形貌特征、化学元素组成以及与基体之间的相互作用的角度出发,以实验测试为基础,综合前人研究的数学模型进行半定量乃至全定量的经验公式推导,以求量化非金属夹杂物的各项参数对钢材疲劳性能的影响程度。通过总结公式发现,非金属夹杂物的形貌特征对钢材疲劳性能影响最大,夹杂物与基体间相互作用影响次之,夹杂物的化学元素组成与力学性能对疲劳性能影响较小。而随着钢材冶炼技术的发展,研究人员已经将夹杂物尺寸控制到微米级别,这就极大地改善了非金属夹杂物对钢材疲劳性能的影响。但是,如何针对非金属夹杂物与基体间的作用效果进行疲劳性能的改善,仍是钢铁材料疲劳性能探究的技术难题。解析非金属夹杂物与基体间的相互作用机理,从而有针对性地提高非金属夹杂物的强化作用,可以使得我国重大工程项目使用的钢材产生质的飞跃,满足国家在重大工程上日益广泛的应用需求。
| [1] |
王驰, 冉广, 雷鹏辉, 等. SA508 Gr.3 Cl.1钢的疲劳和高温拉伸性能[J]. 材料工程, 2018, 46(5): 151-158. WANG C, RAN G, LEI P H, et al. Fatigue and high-temperature tensile properties of SA508 Gr[J]. Journal of Materials Engineering, 2018, 46(5): 151-158. |
| [2] |
KREWERTH D, LIPPMANN T, WEIDNER A, et al. Influence of non-metallic inclusions on fatigue life in the very high cycle fatigue regime[J]. International Journal of Fatigue, 2016, 84: 40-52. DOI:10.1016/j.ijfatigue.2015.11.001 |
| [3] |
MOGHADDAM S M, SADEGHI F. A review of microstructural alterations around nonmetallic inclusions in bearing steel during rolling contact fatigue[J]. Tribology Transactions, 2016, 59(6): 1142-1156. DOI:10.1080/10402004.2016.1141447 |
| [4] |
STINVILLE J C, MARTIN E, KARADGE M, et al. Competing modes for crack initiation from non-metallic inclusions and intrinsic microstructural features during fatigue in a polycrystalline nickel-based superalloy[J]. Metallurgical and Materials Transactions A, 2018, 49(9): 3865-3873. DOI:10.1007/s11661-018-4780-3 |
| [5] |
SHIMOJI I, NATORI M, HIDAKA H, et al. Effect of neighboring-microstructure on the rolling contact fatigue around non-metallic inclusion[J]. MATEC Web of Conferences, 2018, 165: 4-15. |
| [6] |
何群雄, 孙时秋. GB/T 10561-2005钢中非金属夹杂物含量的测定——标准评级图显微检验法介绍[J]. 理化检验-物理分册, 2007, 43(1): 43-47. HE Q X, SUN S Q. Introduction to steel-determination of content of nonmetallic inclusions-micrographic method using standards diagrams GB/T 10561-2005[J]. Physical Testing and Chemical Analysis (Part A:Physical Testing), 2007, 43(1): 43-47. DOI:10.3969/j.issn.1001-4012.2007.01.013 |
| [7] |
孟耀青, 王昆鹏, 郑永瑞. 1950 MPa级弹簧钢55SiCrA疲劳断口夹杂物来源分析[J]. 钢铁研究学报, 2017, 29(10): 859-864. MENG Y Q, WANG K P, ZHENG Y R. Analysis of sources of inclusions induced fatigue fracture in 1950 MPa grade spring steel 55SiCrA[J]. Journal of Iron and Steel Research, 2017, 29(10): 859-864. |
| [8] |
YANG Y D, PAUL W, ZHANG G F, et al. Inclusion characterization in high strength low alloy steel for pipeline application[J]. Journal of Iron and Steel Research, International, 2011, 18(Suppl 1/2): 762-768. |
| [9] |
ZHANG G X, HUA Y S, SHEN Y W, et al. The sensitivity of the focused ultrasonic method used in inclusion testing of the thick steel specimen[J]. Applied Mechanics and Materials, 2013, 455: 253-260. DOI:10.4028/www.scientific.net/AMM.455.253 |
| [10] |
张立峰, 杨文, 张学伟, 等. 钢中夹杂物的系统分析技术[J]. 钢铁, 2014, 49(2): 1-8. ZHANG L F, YANG W, ZHANG X W, et al. Systematic analysis of non-metallic inclusions in steel[J]. Iron and Steel, 2014, 49(2): 1-8. |
| [11] |
LIU H, LIU J, MICHELIC S K, et al. Characterization and analysis of non-metallic inclusions in low-carbon Fe-Mn-Si-Al TWIP steels[J]. Steel Research International, 2016, 87(12): 1723-1732. DOI:10.1002/srin.201600131 |
| [12] |
SHIM J H, OH Y J, SUH J Y, et al. Ferrite nucleation potency of non-metallic inclusions in medium carbon steels[J]. Acta Materialia, 2001, 49(12): 2115-2122. DOI:10.1016/S1359-6454(01)00134-3 |
| [13] |
李阳, 孙海波, 兰鹏, 等. 不同电解方法萃取SPHC钢中非金属夹杂物的研究[J]. 武汉科技大学学报, 2015, 38(6): 408-412. LI Y, SUN H B, LAN P, et al. Extraction of non-metallic inclusions in SPHC steel by different electrolysis methods[J]. Journal of Wuhan University of Science and Technology, 2015, 38(6): 408-412. DOI:10.3969/j.issn.1674-3644.2015.06.002 |
| [14] |
MURAKAMI Y, ENDO M. Effects of defects, inclusions and inhomogeneities on fatigue strength[J]. International Journal of Fatigue, 1994, 16(3): 163-182. DOI:10.1016/0142-1123(94)90001-9 |
| [15] |
SHI G, ATKINSON H V, SELLARS C M, et al. Application of the generalized Pareto distribution to the estimation of the size of the maximum inclusion in clean steels[J]. Acta Materialia, 1999, 47(5): 1455-1468. DOI:10.1016/S1359-6454(99)00034-8 |
| [16] |
SHI G, ATKINSON H V, SELLARS C M, et al. Computer simulation of the estimation of the maximum inclusion size in clean steels by the generalized Pareto distribution method[J]. Acta Materialia, 2001, 49(10): 1813-1820. DOI:10.1016/S1359-6454(01)00079-9 |
| [17] |
DEY A K, DAS K P. Modeling extreme hurricane damage using the generalized Pareto distribution[J]. American Journal of Mathematical and Management Sciences, 2016, 35(1): 55-66. DOI:10.1080/01966324.2015.1075926 |
| [18] |
PARK M H, KIM J H T. Estimating extreme tail risk measures with generalized Pareto distribution[J]. Computational Statistics ´ Data Analysis, 2016, 98: 91-104. DOI:10.1016/j.csda.2015.12.008 |
| [19] |
CHEN H, CHENG W, RONG Y, et al. Fitting the generalized Pareto distribution to data based on transformations of order statistics[J]. Journal of Applied Statistics, 2019, 46(3): 432-448. DOI:10.1080/02664763.2018.1495700 |
| [20] |
SUN Z, WEI L, DENG H, et al. Fisheye failure analysis and life design approach for case-carburized gear steel based on statistical evaluation of defect size[J]. Engineering Failure Analysis, 2016, 59: 28-40. DOI:10.1016/j.engfailanal.2015.11.017 |
| [21] |
FROST N E, POOK L P, DENTON K. A fracture mechanics analysis of fatigue crack growth data for various materials[J]. Engineering Fracture Mechanics, 1971, 3(2): 109-126. DOI:10.1016/0013-7944(71)90003-8 |
| [22] |
TODA H, OOGO H, HORIKAWA K, et al. The true origin of ductile fracture in aluminum alloys[J]. Metallurgical and Materials Transactions A, 2014, 45(2): 765-776. DOI:10.1007/s11661-013-2013-3 |
| [23] |
LI W, PARKER S, ROSE A, et al. Effects of solute Nb atoms and Nb precipitates on isothermal transformation kinetics from austenite to ferrite[J]. Metallurgical and Materials Transactions A, 2016, 47(7): 3387-3396. DOI:10.1007/s11661-016-3548-x |
| [24] |
PETERSON R E. The role of stress distribution in fatigue[J]. Experimental Mechanics, 1961, 1(4): 105-115. DOI:10.1007/BF02323115 |
| [25] |
RODOPOULOS C A. Fatigue damage map as a virtual tool for fatigue damage tolerance[M]. New York: Virtual Testing and Predictive Modeling, Springer US Press, 2009: 15-18.
|
| [26] |
SMITH R A. On the short crack limitations of fracture mechanics[J]. International Journal of Fracture, 1977, 13(13): 717-720. |
| [27] |
HADDAD M H E, TOPPER T H, SMITH K N. Prediction of non-propagating cracks[J]. Engineering Fracture Mechanics, 1979, 11(3): 573-584. DOI:10.1016/0013-7944(79)90081-X |
| [28] |
TANAKA M, NAKAMURA F, MIZOKAWA S, et al. Establishment and assessment of a rat model of fatigue[J]. Neuroscience Letters, 2003, 352(3): 159-162. DOI:10.1016/j.neulet.2003.08.051 |
| [29] |
McEVILY A J, ENDO M, MURAKAMI Y. On the relationship and the short fatigue crack threshold[J]. Fatigue ´ Fracture of Engineering Materials ´ Structures, 2010, 26(3): 269-278. |
| [30] |
USAMI S, SHIDA S. Elastic-plastic analysis of the fatigue limit for a material with small flaws[J]. Fatigue ´ Fracture of Engineering Materials ´ Structures, 1979, 1(4): 471-481. DOI:10.1111/j.1460-2695.1979.tb01334.x |
| [31] |
ABDEL R H, TOPPER T H, PLUMTREE A. A short fatigue crack model based on the nature of the free surface and its microstructure[J]. Scripta Metallurgica et Materialia, 1991, 25(3): 597-602. DOI:10.1016/0956-716X(91)90098-L |
| [32] |
REGE K, PAVLOU D G. A one-parameter nonlinear fatigue damage accumulation model[J]. International Journal of Fatigue, 2017, 98: 234-246. DOI:10.1016/j.ijfatigue.2017.01.039 |
| [33] |
AYAR P, MORENO-NAVARRO F, SOL-S´#193;NCHEZ M, et al. Exploring the recovery of fatigue damage in bituminous mixtures:the role of rest periods[J]. Materials and Structures, 2018, 51(1): 25. |
| [34] |
AERAN A, SIRIWARDANE S C, MIKKELSEN O, et al. A new nonlinear fatigue damage model based only on S-N curve parameters[J]. International Journal of Fatigue, 2017, 103: 327-341. DOI:10.1016/j.ijfatigue.2017.06.017 |
| [35] |
MURAKAMI Y, NOMOTO T, UEDA T, et al. On the mechanism of fatigue failure in the superlong life regime (N>107 cycles)[J]. Fatigue ´ Fracture of Engineering Materials ´ Structures. |
| [36] |
WANG Q Y, BERARD J Y, DUBARRE A, et al. Gigacycle fatigue of ferrous alloys[J]. Fatigue ´ Fracture of Engineering Materials ´ Structures, 1999, 22: 667-672. DOI:10.1046/j.1460-2695.1999.t01-1-00185.x |
| [37] |
AKINIWA Y, MIYAMOTO N, TSURU H, et al. Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime[J]. International Journal of Fatigue, 2006, 28(11): 1555-1565. DOI:10.1016/j.ijfatigue.2005.04.017 |
| [38] |
LIU Y B, LI Y D, LI S X, et al. Prediction of the S-N curves of high strength steels in the very high cycle fatigue regime[J]. International Journal of Fatigue, 2010, 32: 1351-1357. DOI:10.1016/j.ijfatigue.2010.02.006 |
| [39] |
DESMORAT R, KANE A, SEYEDI M, et al. Two scale damage model and related numerical issues for thermo-mechanical high cycle fatigue[J]. European Journal of Mechanics, 2007, 26(6): 909-935. DOI:10.1016/j.euromechsol.2007.01.002 |
| [40] |
MILO E I, GARB C, WINTER G, et al. Effects of inclusions on the very high cycle fatigue properties of a high strength martensitic steel within the transition area[J]. Procedia Structural Integrity, 2017, 7: 327-334. DOI:10.1016/j.prostr.2017.11.096 |
| [41] |
CARRION P E, SHAMSAEI N, DANIEWICZ S R, et al. Fatigue behavior of Ti-6Al-4V including mean stress effects[J]. International Journal of Fatigue, 2017, 99: 87-100. DOI:10.1016/j.ijfatigue.2017.02.013 |
| [42] |
NARAGANI D, SANGID M D, SHADE P A, et al. Investigation of fatigue crack initiation from a non-metallic inclusion via high energy X-ray diffraction microscopy[J]. Acta Materialia, 2017, 137: 71-84. DOI:10.1016/j.actamat.2017.07.027 |
| [43] |
GILLNER K, HENRICH M, MUNSTERMANN S. Numerical study of inclusion parameters and their influence on fatigue lifetime[J]. International Journal of Fatigue, 2018, 111: 70-80. DOI:10.1016/j.ijfatigue.2018.01.036 |
| [44] |
YANG Y, LIN Y, ZHANG Y. Average capacity of the ground to train communication link of a curved track in the turbulence of gamma-gamma distribution[J]. Optics Communications, 2017, 389: 68-73. DOI:10.1016/j.optcom.2016.12.025 |
| [45] |
KIESSLING R. Nonmetallic inclusions and their effects on the properties of ferrous alloys[J]. Encyclopedia of Materials Science and Technology, 2001, 6278-6283. |
| [46] |
WU Q, QIANG X. Interactive mechanisms of sulfide inclusions and environmental factors in low cycle fatigue process of pressure vessel steels in high temperature water[J]. Materials Science Forum, 2005, 475/479: 253-256. |
| [47] |
HASHIMOTO K. Effect of sulphide inclusions on rolling contact fatigue life of bearing steels[J]. Materials Science and Technology, 2013, 28(1): 39-43. |
| [48] |
MAKINO T, NEISHI Y, SHIOZAWA D, et al. Rolling contact fatigue damage from artificial defects and sulphide inclusions in high strength steel[J]. Procedia Structural Integrity, 2017, 7: 468-475. DOI:10.1016/j.prostr.2017.11.114 |
| [49] |
CYRIL N S, FATEMI A. Experimental evaluation and modeling of sulfur content and anisotropy of sulfide inclusions on fatigue behavior of steels[J]. International Journal of Fatigue, 2009, 31(3): 526-537. DOI:10.1016/j.ijfatigue.2008.04.001 |
| [50] |
ROESSLE M L, FATEMI A. Strain-controlled fatigue properties of steels and some simple approximations[J]. International Journal of Fatigue, 2000, 22(6): 495-511. DOI:10.1016/S0142-1123(00)00026-8 |
| [51] |
李冬玲, 李美玲, 贾云海, 等. 钢中硅系夹杂物含量的原位统计分布分析[J]. 冶金分析, 2011, 31(1): 1-6. LI D L, LI M L, JIA Y H, et al. Quantitative analysis of silicon inclusions in steel by original position statistic distribution analysis technique[J]. Metallurgical Analysis, 2011, 31(1): 1-6. DOI:10.3969/j.issn.1000-7571.2011.01.001 |
| [52] |
BELLOT J P, KROLL J S, GISSL B M, et al. Toward better control of inclusion cleanliness in a gas stirred ladle using multiscale numerical modeling[J]. Materials, 2018, 11(7): 1179-1182. DOI:10.3390/ma11071179 |
| [53] |
SHI C B, CHEN X C, GUO H J, et al. Control of MgO´#183;Al2O3 spinel inclusions during protective gas electroslag remelting of die steel[J]. Metallurgical and Materials Transactions B, 2013, 44(2): 378-389. DOI:10.1007/s11663-012-9780-x |
| [54] |
SEO C W, KIM S H, JO S K, et al. Modification and minimization of spinel(Al2O3·xMgO) inclusions formed in Ti-added steel melts[J]. Metallurgical and Materials Transactions B, 2010, 41(4): 790-797. DOI:10.1007/s11663-010-9377-1 |
| [55] |
朱青德, 魏国立. 硅铝铁脱氧生产70#钢中夹杂物研究[J]. 甘肃冶金, 2018, 40(3): 11-16. ZHU Q D, WEI G L. Si-Al-Fe deoxidation produce 70# steel study on inclusions[J]. Gansu Metallurgy, 2018, 40(3): 11-16. DOI:10.3969/j.issn.1672-4461.2018.03.004 |
| [56] |
LI W, LIANG H, CHEN J, et al. Effect of SiC particles on fatigue crack growth behavior of SiC particulate-reinforced Al-Si alloy composites produced by spray forming[J]. Procedia Materials Science, 2014, 3: 1694-1699. DOI:10.1016/j.mspro.2014.06.273 |
| [57] |
WANG J, ZHANG Y, LIU S, et al. Competitive giga-fatigue life analysis owing to surface defect and internal inclusion for FV520B-I[J]. International Journal of Fatigue, 2016, 87: 203-209. DOI:10.1016/j.ijfatigue.2016.01.028 |
| [58] |
SUN C, LEI Z, XIE J, et al. Effects of inclusion size and stress ratio on fatigue strength for high-strength steels with fish-eye mode failure[J]. International Journal of Fatigue, 2013, 48: 19-27. DOI:10.1016/j.ijfatigue.2012.12.004 |
| [59] |
NAKAMURA T, OGUMA H, SHINOHARA Y. The effect of vacuum-like environment inside sub-surface fatigue crack on the formation of ODA fracture surface in high strength steel[J]. Procedia Engineering, 2010, 2(1): 2121-2129. DOI:10.1016/j.proeng.2010.03.228 |
| [60] |
YAMASHITA Y, MURAKAMI Y. Small crack growth model from low to very high cycle fatigue regime for internal fatigue failure of high strength steel[J]. International Journal of Fatigue, 2016, 93: 406-414. DOI:10.1016/j.ijfatigue.2016.04.016 |
| [61] |
MURAKAMI Y. Chapter 6-effects of nonmetallic inclusions on fatigue strength[M]//Metal Fatigue.Amsterdam: Elsevier, 2002: 75-127.
|
| [62] |
FURUYA Y, ABE T, MATSUOKA S. Inclusion-controlled fatigue properties of 1800 MPa-class spring steels[J]. Metallurgical and Materials Transactions A, 2004, 35(12): 3737-3744. DOI:10.1007/s11661-004-0279-1 |
| [63] |
LIU Y B, LI S X, LI Y D, et al. Factors influencing the GBF size of high strength steels in the very high cycle fatigue regime[J]. Materials Science and Engineering:A, 2011, 528(3): 935-942. |
| [64] |
ZHOU C, ZHANG Y J, HUI W J, et al. Influence of hydrogen on GBF in very high cycle fatigue of high strength steel[J]. Journal of Iron and Steel Research, International, 2013, 20(12): 92-97. DOI:10.1016/S1006-706X(13)60221-6 |
| [65] |
LI W, GAO N, ZHAO H Q, et al. Crack initiation and early growth behavior of TC4 titanium alloy under high cycle fatigue and very high cycle fatigue[J]. Journal of Materials Research, 2018, 33: 1-11. |
| [66] |
LIU Y B, YANG Z G, LI Y D, et al. Dependence of fatigue strength on inclusion size for high-strength steels in very high cycle fatigue regime[J]. Materials Science and Engineering:A, 2009, 517(1): 180-184. |
| [67] |
ZHAO P, LIU Z, MISRA R D K, et al. Non-inclusion induced crack initiation in multiphase high-strength steel during very high cycle fatigue[J]. Materials Science and Engineering:A, 2017, 712: 406-413. |
| [68] |
YANG Z G, LI S X, LI Y D, et al. Relationship among fatigue life, inclusion size and hydrogen concentration for high-strength steel in the VHCF regime[J]. Materials Science and Engineering:A, 2010, 527(3): 559-564. |
| [69] |
MURAKAMI Y, NOMOTO T, UEDA T. Factors influencing the mechanism of superlong fatigue failure in steels[J]. Fatigue ´ Fracture of Engineering Materials ´ Structures, 1999, 22(7): 1879-1892. |
| [70] |
SHIOZAWA K, LU L, ISHIHARA S. S-N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel[J]. Fatigue ´ Fracture of Engineering Materials ´ Structures, 2001, 24(12): 781-790. DOI:10.1046/j.1460-2695.2001.00459.x |
| [71] |
SAKAI T, LIAN B, TAKEDA M, et al. Statistical duplex-characteristics of high carbon chromium bearing steel in rotating bending in very high cycle regime[J]. International Journal of Fatigue, 2010, 32(3): 497-504. DOI:10.1016/j.ijfatigue.2009.08.001 |
| [72] |
GRAD P, REUSCHER B, BRODYANSKI A, et al. Mechanism of fatigue crack initiation and propagation in the very high cycle fatigue regime of high-strength steels[J]. Scripta Materialia, 2012, 67(10): 838-841. DOI:10.1016/j.scriptamat.2012.07.049 |
| [73] |
TSUKADA K, HAYASHI M, NAKAMURA Y, et al. Small eddy current testing sensor probe using a tunneling magnetoresistance sensor to detect cracks in steel structures[J]. IEEE Transactions on Magnetics, 2018, 54(11): 6202205. |
| [74] |
LI J, SU H, CHAI F, et al. Corrosion behavior of low-carbon Cr micro-alloyed steel for grounding grids in simulated acidic soil[J]. Journal of Iron and Steel Research, International, 2018, 25(7): 755-766. DOI:10.1007/s42243-018-0108-1 |
| [75] |
ABDESSELAM H, CREPIN J, PINEAU A, et al. On the crystallographic, stage Ⅰ-like, character of fine granular area formation in internal fish-eye fatigue cracks[J]. International Journal of Fatigue, 2018, 106: 132-142. DOI:10.1016/j.ijfatigue.2017.09.013 |
| [76] |
SPRIESTERSBACH D, BRODYANSKI A, L´#214;SCH J, et al. Very high cycle fatigue of bearing steels with artificial defects in vacuum[J]. Materials Science and Technology, 2016, 32(11): 1111-1118. DOI:10.1080/02670836.2015.1119931 |
| [77] |
NEHILA A, LI W, GAO N, et al. Very high cycle fatigue of surface carburized CrNi steel at variable stress ratio:failure analysis and life prediction[J]. International Journal of Fatigue, 2018, 111: 112-123. DOI:10.1016/j.ijfatigue.2018.02.006 |
 2020, Vol. 48
2020, Vol. 48