文章信息
- 蔡庄立, 赵伶玲, 虞兮凡, 陈超
- CAI Zhuang-li, ZHAO Ling-ling, YU Xi-fan, CHEN Chao
- 模拟聚乙烯块体相变和导热的粗粒化模型和势场建立
- Coarse-grained model and force field development for predicting phase change and thermal transport in polyethylene
- 材料工程, 2020, 48(1): 34-40
- Journal of Materials Engineering, 2020, 48(1): 34-40.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2019.000102
-
文章历史
- 收稿日期: 2019-01-29
- 修订日期: 2019-04-29
高分子材料因具有高韧性、耐腐蚀、低密度等特点,而被广泛应用于工程实践。传统的高分子聚合物材料一般由无序排列且呈团状聚集的大分子有机物组成,声子散射严重,而且缺少自由电子,因而导热性能差,其导热系数仅为0.1~0.3 W·m-1·K-1,限制了其在导热领域的应用[1]。实验研究表明,拉伸比400的聚乙烯纳米纤维的导热系数可以达到104 W·m-1·K-1,高于大多数金属, 如此高的导热系数被归因于聚乙烯重新排布到接近理想单晶的结构[2]。
相比于实验研究,分子动力学(MD)模拟易于实现,且使得材料微观分子构型可视化,而广泛应用于高分子聚合物的研究[3-4]。目前学者们采用全原子分子动力学(all-atom molecular dynamics,AA-MD)模拟研究了单链聚乙烯[5]、纳米尺寸聚乙烯块体[6]等的热导,限于当前计算机的水平,其分子量一般小于1×104 g·mol-1,但高密度聚乙烯通常具有约为1×106 g·mol-1的分子量[7]。而且随着分子量的增大,线性聚乙烯的导热系数逐渐增大[8]。同时实验中导热聚乙烯纤维热拉伸加工的时间尺度也是传统的AA-MD模拟(即最小计算单元为原子)无法涉及的,因此需要开发更高效的模拟方法。粗粒化分子动力学(coarse-grained molecular dynamics,CG-MD)以分子中几个原子为最小计算单元,可以把MD模拟的时间和空间尺度从AA-MD模拟的纳秒和纳米水平拓展到微秒和微米水平[9]。然而,目前对高分子聚合物导热的粗粒化分子模拟研究鲜有深入涉及。
本工作采用分子动力学模拟的方法,以AA-MD模拟为基准,建立了适用于介观尺度聚乙烯(PE)块体相变和导热分子模拟的CG势场,并通过实验数据验证了势场的准确性,为聚乙烯导热研究提供了更高效的工具。
1 模型构建及方法 1.1 CG势场的建立本工作中,定义PE分子链上连续的5个亚甲基(—CH2—)作为一个粗粒化珠子,原子间作用力由珠子与珠子之间作用力代替,如图 1所示。
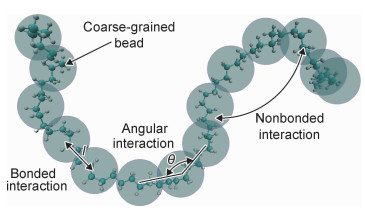
|
图 1 粗粒化模型和势场示意图 Fig. 1 Schematics of coarse-grained model and force field |
CG势场VCG包括以下三项:
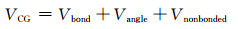
|
(1) |
其中,Vbond,Vangle和Vnonbonded分别为键伸缩势能、键角弯曲势能和珠子间非键结势能。CG势场的参数化通过AA-MD模拟和CG-MD模拟对比验证实现。考虑到PE热拉伸的实际加工条件,AA-MD和CG-MD模拟分别在两个热力学状态:(1)500 K和实验密度[10]0.71 g·cm-3;(2)300 K和公式推测密度[11]0.82 g·cm-3运行。CG势场按照相互作用由强到弱的顺序[12]确定:Vbond→Vangle→Vnonbonded。根据以上的方案,AA-MD模拟中的原子轨迹被映射为CG轨迹。从AA-MD模拟获得的键长和键角分布作为目标性质被用来参数化CG键结势场。
键伸缩势能用Morse势函数描述:
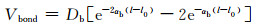
|
(2) |
式中:l0是最小势能-Db所在的键长距离;αb描述了势函数的曲率。AA-MD模拟所得的键长分布中峰的位置作为l0。由碳碳单键的解离能[13]得到Db=351.6 kJ·mol-1。由于伸直的单链PE的导热系数对于PE块体的导热系数是关键的,通过匹配300 K下不同长度的单链PE(CnH2n,n=400,500,600,680和800)导热系数的AA模拟值和CG模拟值确定αb。单链PE首尾通过跨越周期性边界的共价键连接,以保证分子链为伸直状态。
键角弯曲势能采用可结晶的余弦函数[14]描述:
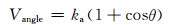
|
(3) |
其中,角系数ka通过匹配CG-MD模拟和AA-MD模拟的键角分布获得。
非键结势能通过多态-迭代玻尔兹曼变换方法[15]获得。从AA-MD模拟得到(—CH2—)5质心的径向分布函数(RDF)作为目标值被用来参数化CG非键结势能。初始的非键结势能采用目标RDF(g*(r))的玻尔兹曼变换并在两个热力学状态平均得到:
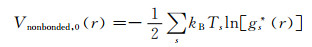
|
(4) |
式中:kB是玻尔兹曼常数;下标s表示不同的热力学状态,Ts表示热力学状态s下的温度。非键结势能的截断距离rcutoff取1.2 nm。键结的最近邻珠子对的非键结势能被排除。然后采用式(4)的势能在两个热力学状态分别运行60 ns,通过下式获得第i+1次迭代的非键结势能:
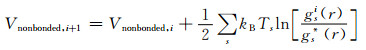
|
(5) |
迭代收敛性通过以下函数评估:
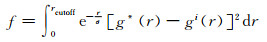
|
(6) |
其中σ是珠子的范德华半径,取g*(r)第一个峰的位置等于0.58 nm。当f小于0.02或者不再增加时迭代终止。
1.2 模拟细节AA-MD模拟系统包含400根,长度n=72的分子链,采用AIREBO势场[16],时间步长为0.5 fs。该势场被证明能够准确预测PE晶体块体的导热系数[2]。AA-MD模拟分别在热力学状态(1)和(2)运行15 ns和5 ns,并分别在后3 ns每隔0.05 ns采样模型的构形。与AA-MD模拟系统相对应,CG-MD模拟系统包含400根,由14个粗粒化珠子组成的分子链。CG-MD模拟分别在以上的两个热力学状态运行60 ns,并分别在后40 ns每隔1 ns采样模型的构形,时间步长为20 fs。
为获得包含2025根、由150个粗颗粒组成的分子链的大尺度无定形PE模型用于导热研究,采用double-bridge算法[17],在NPT(T=500 K,P=1.0×105 Pa)系统下弛豫200 ns使系统达到平衡,之后以2 K·ns-1的速率降温到300 K,得到23 nm×24 nm×80 nm的无定形乱序PE块体模型。该系统中聚乙烯块体的分子量达到10500 g·mol-1,高于AA-MD模拟中采用的最大分子量(5602 g·mol-1)[6]。以上模拟均采用分子模拟软件LAMMPS[18]。
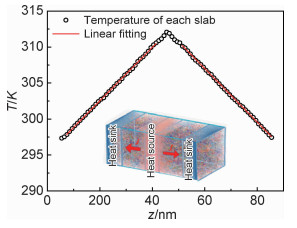
1.3 数据处理聚乙烯导热系数的计算采用Müller-Plathe[19]的非平衡分子动力学(non-equilibrium molecular dynamic,NEMD)模拟方法。该算法的基本思想(图 2)是将模拟盒在z方向等分成20层, 0层和10层分别为热汇和热源, 11层到19层与前一部分成镜像对称。通过交换热汇与热源的原子能量得以使两端形成温度差,从而可以生成从0层到N/2层的热流J及与热流方向相反的温度场,于是导热系数k可以通过傅里叶定律得到:
|
图 2 NEMD模拟温度分布及线性拟合 Fig. 2 Temperature profile and linear fitting in NEMD simulation |
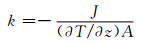
|
(7) |
式中: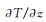
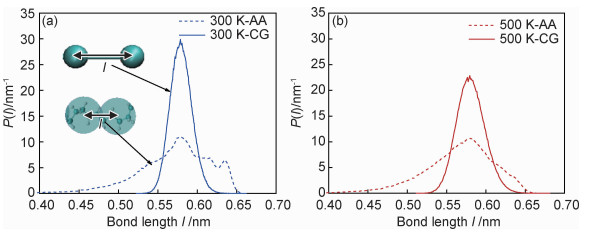
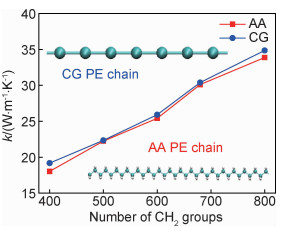
键伸缩势参数l0通过AA-MD模拟的键长概率分布(图 3)峰的位置确定。由图 3可知,与AA-MD模拟结果相比,CG-MD模拟的键长分布峰的位置吻合较好,而峰宽更窄,这是为了实现准确的单链PE导热系数。在其他键伸缩势能参数确定的条件下,单链PE的导热系数随着αb的增大而单调增大。因此,αb可通过匹配300 K下不同长度单链PE的导热系数的CG-MD模拟值与AA-MD模拟值获得,结果示于图 4。由该图可知,CG势场能够准确地描述单链PE的导热。
|
图 3 AA-MD模拟和CG-MD模拟中粗粒化珠子间键长的概率分布 (a)300 K;(b)500 K Fig. 3 Bond length distributions between coarse-grained bead from AA-MD simulations and CG-MD simulations (a)300 K; (b)500 K |
|
图 4 AA-MD和CG-MD模拟中不同—CH2—数的伸直单链聚乙烯的导热系数 Fig. 4 Thermal conductivities of extended single PE chains with different numbers of —CH2— groups in AA-MD and CG-MD simulations |
键角弯曲势参数ka通过匹配CG-MD模拟和AA-MD模拟的键角概率分布(图 5)获得。由图 5可知,在300 K下,CG-MD模拟的键角比AA-MD模拟偏向更大值分布,它们键角的平均值偏差为12°,这或许是由于CG模型相比于AA模型具有更低的自由度而无法做到精确的匹配;在500 K下,CG-MD模拟的键角分布与AA-MD模拟结果吻合较好。
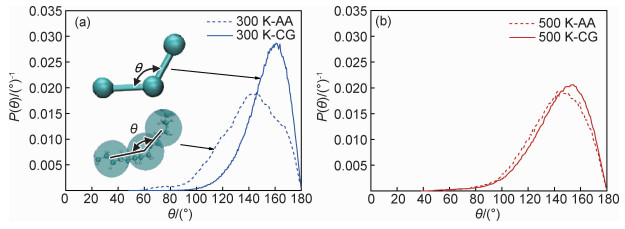
|
图 5 AA-MD模拟和CG-MD模拟中粗粒化珠子间键角的概率分布 (a)300 K;(b)500 K Fig. 5 Angle distributions between coarse-grained bead from AA-MD simulations and CG-MD simulations (a)300 K; (b)500 K |
为得到非键结势能,采用多态-迭代玻尔兹曼变换法进行7次CG-MD模拟后,优化函数f=0.015,达到收敛条件。由于迭代方法中不包含目标压力,目标压力在CG-MD模拟中通常无法准确实现。为修正CG-MD模拟中系统的压力和目标压力(1.0×105 Pa)之间的差异,修正项被加入到最终迭代的数值势函数中[21]:
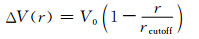
|
(8) |
其中V0是唯一需要调整的参数。当系统当前压力小于目标压力时,V0取正值,反之取负值。此方法能保证不明显改变系统的RDF。进行多次压力修正迭代模拟后,最终得到的数值型的非键结势函数曲线示于图 6,其RDF曲线示于图 7。考虑到势能曲线的形状和非键结势函数使用的便捷性,Morse形式的解析型非键结势函数被拟合,结果示于图 6。
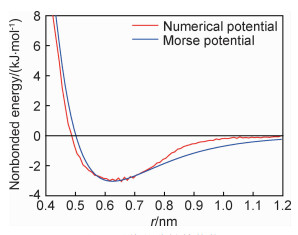
|
图 6 最终的非键结势能 Fig. 6 Final nonbonded potentials |
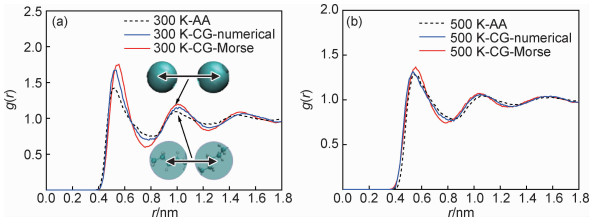
|
图 7 AA-MD模拟和CG-MD模拟的RDF曲线 (a)300 K;(b)500 K Fig. 7 RDF curves from AA-MD simulations and CG-MD simulations (a)300 K; (b)500 K |
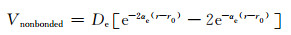
|
(9) |
式中:r0是珠子间的平衡距离;-De是最小势能;αe描述了势函数的曲率。采用Morse型非键结势函数模拟的RDF曲线也示于图 7。由该图可知,在300,500 K下,CG-MD模拟的RDF曲线与AA-MD模拟的结果较符合。综合对比粗粒化珠子的键长分布、键角分布和RDF曲线的CG-MD模拟结果和AA-MD模拟结果,可知CG势场能够在一定程度上较准确地描述PE块体的静态结构性质。最终的CG势场参数列于表 1。
| Interaction | CG potential parameter |
| Bond | 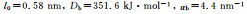 |
| Angular | 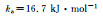 |
| Nonbonded |
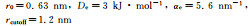 |
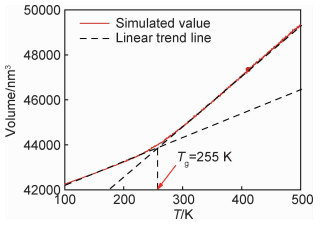
为验证CG势场的准确性,本工作计算了PE块体的热力学性质和导热系数并与实验值作对比。表 2为PE块体在P=1.0×105 Pa, T=300 K和500 K下的密度。由表 2中数据可知,CG势场的模拟值与实验数据吻合较好,相对误差小于3%。玻璃化转变温度Tg和熔化温度Tm是导热高分子聚合物材料加工过程中的两个重要的热力学性质,被用来验证CG势场。将包含2025条、每条由150个珠子组成的分子链的PE块体在NPT系统(P=1.0×105 Pa)下由500 K冷却到200 K,由体积-温度曲线的斜率转折点得到Tg[22](图 8),Tg=255 K,与实验值250 K[23]较吻合。Tm采用迟滞法[24]得到:
|
图 8 CG无定形聚乙烯块体体积与温度的关系 Fig. 8 Volume of CG amorphous bulk PE as a function of temperature |
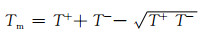
|
(10) |
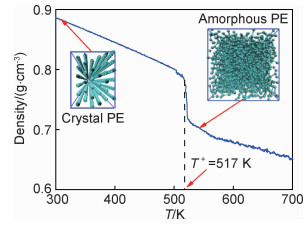
式中:T+是过热相变温度;T-是过冷相变温度。将包含36条、每条由150个珠子组成的分子链的PE晶体在NPT系综(P=1.0×105 Pa)下由300 K加热到700 K,由密度-温度曲线的阶跃点得到T+ (图 9),T+=517 K。由于稀少的结晶成核,T-通常较难得到,可用Tg近似代替[25]。由此,得到Tm=409 K,与实验值410 K[26]非常接近。以上结果表明CG势场能较准确地描述PE块体的热力学性质。
|
图 9 CG聚乙烯晶体块体密度与升温的关系 Fig. 9 Density of CG crystalline bulk PE as a function of temperature |
本工作采用NEMD的方法模拟无序PE块体的导热过程(图 2),计算得到无序PE块体的导热系数k值为0.105 W·m-1·K-1,与实际物性参数值0.1~0.3 W·m-1·K-1吻合较好,表明本工作所开发的CG势场对PE块体导热的描述具有一定的准确性和可靠性。
CG-MD模拟相比于传统的AA-MD模拟可以有更高的计算效率。这主要归因于两方面,一方面是CG势函数相比于AA势函数更加平滑,因此可以采用更大的时间步长;另一方面是CG模型中每个珠子包含多个原子,因此可以减少粒子对间作用力的计算次数。因此,CG-MD模拟和AA-MD模拟的计算效率比φ可以表示为:
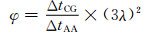
|
(11) |
式中:ΔtCG和ΔtAA分别为CG-MD模拟和AA-MD模拟的时间步长;λ为每个粗粒化珠子中包含的碳原子的数目[27]。在本工作中ΔtCG和ΔtAA分别等于20 fs和0.5 fs,λ等于5。由此得到,理论上,CG-MD模拟和AA-MD模拟的计算效率比为9000。因此,采用本工作的CG力场可实现更大时间、空间尺度和分子量的分子动力学模拟研究。
3 结论(1) CG势场以5个亚甲基(—CH2—)作为一个粗粒化珠子(计算单元);以Morse势函数和余弦势函数分别描述键结珠子之间的键伸缩势能和键角弯曲势能;以Morse势函数描述珠子间非键结势能。
(2) CG势场能够较准确地模拟聚乙烯块体在300 K和500 K下的静态结构(粗粒化珠子的键长、键角和RDF)性质。
(3) 在300 K和500 K下聚乙烯块体密度的模拟值与实验值误差小于3%。CG势场能准确地模拟聚乙烯块体的相变过程,聚乙烯块体玻璃化转变温度、熔化温度的模拟值与实验值相符较好。
(4) 单链聚乙烯的导热系数的CG-MD模拟值与AA-MD模拟值基本一致,无序聚乙烯块体的导热系数的CG-MD模拟值与实验值吻合较好。
(5) 相比于AA-MD模拟,使用本工作的CG势场进行CG-MD模拟,理论计算效率可实现9000倍的提升。
| [1] |
马传国, 容敏智, 章明秋. 导热高分子复合材料的研究与应用[J]. 材料工程, 2002(7): 40-45. MA C G, RONG M Z, ZHANG M Q. Advances in study of thermal conducting polymers composites and their application[J]. Journal of Materials Engineering, 2002(7): 40-45. DOI:10.3969/j.issn.1001-4381.2002.07.011 |
| [2] |
SHEN S, HENERY A, TONG J, et al. Polyethylene nanofibres with very high thermal conductivities[J]. Nature Nanotechnology, 2010, 5(4): 251-255. DOI:10.1038/nnano.2010.27 |
| [3] |
张彦飞, 兰艳花, 付一政, 等. PA6/POE共混物的分子动力学与介观动力学模拟[J]. 材料工程, 2013(7): 44-49. ZHANG Y F, LAN Y H, FU Y Z, et al. Molecular and mesoscopic dynamics properties of PA6/POE blends[J]. Journal of Materials Engineering, 2013(7): 44-49. DOI:10.3969/j.issn.1001-4381.2013.07.009 |
| [4] |
涂润春, 廖全文, 刘志春, 等. 扭转作用对聚乙烯链导热性能的影响[J]. 化工学报, 2017, 68(增刊1): 60-65. TU R C, LIAO Q W, LIU Z C, et al. Impact of torsional function on thermal conductivity of polyethylene chains[J]. CIESC Journal, 2017, 68(Suppl 1): 60-65. |
| [5] |
HENRY A, CHEN G. High thermal conductivity of single polyethylene chains using molecular dynamics simulations[J]. Physical Review Letters, 2008, 101(23): 235502. DOI:10.1103/PhysRevLett.101.235502 |
| [6] |
LIU J, YANG R G. Tuning the thermal conductivity of polymers with mechanical strains[J]. Physical Review B, 2010, 81(17): 174122. DOI:10.1103/PhysRevB.81.174122 |
| [7] |
MARK J E. Physical properties of polymers handbook[M]. New York: Springer, 2007.
|
| [8] |
HANSEN D, KANTAYYA R C, HO C C. Thermal conductivity of high polymers-the influence of molecular weight[J]. Polymer Engineering & Science, 1966, 6(3): 260-262. |
| [9] |
郭洪霞. 高分子粗粒化分子动力学模拟进展[J]. 高分子通报, 2011(10): 154-163. GUO H X. Progress on coarse-grained molecular dynamics simulation of polymers[J]. Chinese Polymer Bulletin, 2011(10): 154-163. |
| [10] |
DEE G T, OUGIZAWA T, WALSH D J. The pressure-volume-temperature properties of polyethylene, poly(dimethyl siloxane), poly(ethylene glycol) and poly(propylene glycol) as a function of molecular weight[J]. Polymer, 1992, 33(16): 3462-3469. DOI:10.1016/0032-3861(92)91104-A |
| [11] |
ZHAO J H, NAGAO S, ZHANG Z L. Thermomechanical properties dependence on chain length in bulk polyethylene:coarse-grained molecular dynamics simulations[J]. Journal of Materials Research, 2010, 25(3): 537-544. DOI:10.1557/JMR.2010.0061 |
| [12] |
REITH D, PÜTZ M, MüLLER-PLATHE F. Deriving effective mesoscale potentials from atomistic simulations[J]. Journal of Computational Chemistry, 2003, 24(13): 1624-1636. DOI:10.1002/jcc.10307 |
| [13] |
BLANKSBY S J, ELLISON G B. Bond dissociation energies of organic molecules[J]. Accounts of Chemical Research, 2003, 6(4): 255-263. |
| [14] |
NGUYEN H T, SMITH T B, HOY R S, et al. Effect of chain stiffness on the competition between crystallization and glass-formation in model unentangled polymers[J]. Journal of Chemical Physics, 2015, 143(14): 144902. DOI:10.1063/1.4932372 |
| [15] |
MOORE T C, IACOVELLA C R, McCABE C. Derivation of coarse-grained potentials via multistate iterative Boltzmann inversion[J]. The Journal of Chemical Physics, 2014, 140(22): 06B. |
| [16] |
STUART S J, TUTEIN A B, HARRISON J A. A reactive potential for hydrocarbons with intermolecular interactions[J]. Journal of Chemical Physics, 2000, 112(14): 6472-6486. DOI:10.1063/1.481208 |
| [17] |
AUHL R, EVERAERS R, GREST G S, et al. Equilibration of long chain polymer melts in computer simulations[J]. Journal of Chemical Physics, 2003, 119(24): 12718-12728. DOI:10.1063/1.1628670 |
| [18] |
PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19. |
| [19] |
MÜLLER-PLATHE F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity[J]. Journal of Chemical Physics, 1997, 106(14): 6082-6085. DOI:10.1063/1.473271 |
| [20] |
HENERY A, CHEN G. High thermal conductivity of single polyethylene chains using molecular dynamics simulations[J]. Physical Review Letters, 2008, 101(23): 235502. DOI:10.1103/PhysRevLett.101.235502 |
| [21] |
MILANO G, MÜLLER-PLATHE F. Mapping atomistic simulations to mesoscopic models:a systematic coarse-graining procedure for vinyl polymer chains[J]. Journal of Physical Chemistry B, 2005, 109(39): 18609-18619. DOI:10.1021/jp0523571 |
| [22] |
HOSSAIN D, TSCHOPP M A, WARD D K, et al. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene[J]. Polymer, 2010, 51: 6071-6083. DOI:10.1016/j.polymer.2010.10.009 |
| [23] |
MAGILL J H, POLLACK S S, WYMAN D P. Glass temperature and crystal modification of linear polymethylene[J]. Journal of Polymer Science Part A:General Papers, 1965, 3(11): 3781-3786. DOI:10.1002/pol.1965.100031109 |
| [24] |
LUO S N, STRACHAN A, SWIFT D C. Nonequilibrium melting and crystallization of a model Lennard-Jones system[J]. Journal of Chemical Physics, 2004, 120(24): 11640-11649. DOI:10.1063/1.1755655 |
| [25] |
ZHENG L, LUO S N, THOMPSON D L. Molecular dynamics simulations of melting and the glass transition of nitromethane[J]. Journal of Chemical Physics, 2006, 124(15): 154504. DOI:10.1063/1.2174002 |
| [26] |
GOPALAN M R, MANDELKEN L. Effect of crystallization temperature and molecular weight on the melting temperature of linear polyethylene[J]. Journal of Physical Chemistry C, 1967, 71(12): 3833-3841. DOI:10.1021/j100871a018 |
| [27] |
SALERNO K M, AGRAWAL A, PERAHIA D, et al. Resolving dynamic properties of polymers through coarse-grained computational studies[J]. Physical Review Letters, 2016, 116(5): 058302. DOI:10.1103/PhysRevLett.116.058302 |
 2020, Vol. 48
2020, Vol. 48


