文章信息
- 周峰, 王克鲁, 鲁世强, 万鹏, 陈虚怀
- ZHOU Feng, WANG Ke-lu, LU Shi-qiang, WAN Peng, CHEN Xu-huai
- Ti-22Al-24Nb-0.5Y合金流变行为及BP神经网络高温本构模型
- Flow behavior and BP neural network high temperature constitutive model of Ti-22Al-24Nb-0.5Y alloy
- 材料工程, 2019, 47(8): 141-146
- Journal of Materials Engineering, 2019, 47(8): 141-146.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2017.001548
-
文章历史
- 收稿日期: 2017-12-17
- 修订日期: 2019-03-23
Ti2AlNb基合金具有高的高温强度、延展性、比刚度及耐蚀性等优异的服役性能,被认为是航空领域的高端结构材料,极具开发潜力及应用前景,近年来一直是钛合金研究领域中的热点[1-3]。Ti2AlNb基合金属于难变形材料,其性能及组织对变形工艺参数较为敏感,在合金热变形过程中,了解其热加工条件下的变形特点,可为其热加工工艺的制订提供参考。因此,建立高精度的本构模型对合金的基础研究具有重要的意义。
传统建立的本构关系模型,多采用Arrhenius型方程应用数理统计或回归模型获得经验公式[4-6],但由于合金对热加工工艺参数的敏感性,因而材料的变形行为随着温度和应变速率的升高呈现出明显的非线性,导致建模过程较为复杂,工作量较大,所建立的模型精度也很难达到要求。而近年来迅速发展起来的BP神经网络技术,则可以很好地解决这一难题,BP神经网络即误差反向传播网络,是一种多层前向型神经网络,它具有自学习、自组织和非线性适应性信息处理能力,能够对具有有限个不连续点的函数进行逼近,在非线性系统的建模、预测预报等方面具有广阔的应用前景[7]。利用BP神经网络技术探索出实验数据之间的内在规律,能够避免传统建立本构模型的不足,且有效地建立高精度本构模型。为此,王克鲁等采用BP神经网络建立了Ti-6.5Al-3.5Mo-1.5Zr-0.3Si合金的本构模型,发现BP神经网络模型对该合金流变应力预测的总拟合度为3.2%,系统误差较小[8];刘雪峰等建立的Cu-12%Al合金BP神经网络模型的真实应力预测值与实验值之间的平均相对误差小于1.8%,较好地反映了合金实际变形过程的特征[9]。但流变应力影响因素的选择涉及建立神经网络本构模型的精确度,正交实验恰好能解决这一问题[10-11],因此利用正交实验可有效地探寻出影响流变应力因素的主次关系,为建立精确度较高的本构关系模型奠定基础。
本工作通过正交实验法,探讨影响流变应力因素的主次关系,利用BP神经网络算法原理,以Ti-22Al-24Nb-0.5Y合金等温恒应变热压缩的实验数据为基础,建立合金在高温塑性变形过程中的本构模型。
1 实验材料与方法 1.1 实验材料实验材料为铸态Ti2AlNb基合金,其原始组织如图 1所示,合金名义成分为Ti-22Al-24Nb-0.5Y,从图 1可以看到,弥散分布的白色颗粒物和α2/O相层片组织分布在B2相基体中,经EDS分析,白色颗粒为Y2O3稀土相,其中α2/O相层片尺寸约5~15μm,稀土相颗粒尺寸约1~3μm。压缩试样尺寸为ϕ8mm×12mm的圆柱体,利用Gleeble-3500热模拟试验机进行等温恒应变速率压缩实验。压缩变形温度为900, 930, 960, 990, 1020, 1050, 1080℃和1100℃;应变速率为0.001, 0.01, 0.1, 1.0s-1和10s-1;高度压下量为70%,对应的真应变为1.2,以5℃/s加热至设定的变形温度后保温300s,为使试样内部温度均匀,压缩结束后立即水冷。

|
图 1 Ti-22Al-24Nb-0.5Y合金铸态组织 Fig. 1 As-cast microstructure of Ti-22Al-24Nb-0.5Y alloy |
合金在变形过程中,其流变应力会受到各种因素的影响,包括变形温度、应变速率、应变量、压缩过程中试样与压头间的摩擦、保温时间以及材料尺寸等。为了确定影响流变应力各因素的主次关系,本实验设计了典型的3水平4因素(L9(34))正交实验,其中因素A代表应变速率,因素B代表变形温度,因素C代表应变量,因素D代表其他因素(空列:不同变形条件下的摩擦、温升等),正交实验因素水平及实验结果分析分别见表 1与表 2。
| Level | Experiment factor | ||
| Strain rate(A)/ s-1 | Deformation temperature(B)/℃ | Strain(C) | |
| 1 | 0.001 | 930 | 0.05 |
| 2 | 1.0 | 990 | 0.55 |
| 3 | 0.1 | 1080 | 0.85 |
| No | A | B | C | D | Flow stress/MPa |
| 1 | 1(0.001s-1) | 1(930℃) | 1(0.05) | 1 | 187.75 |
| 2 | 1(0.001s-1) | 2(990℃) | 2(0.55) | 2 | 72.20 |
| 3 | 1(0.001s-1) | 3(1080℃) | 3(0.85) | 3 | 24.74 |
| 4 | 2(1.0s-1) | 1(930℃) | 2(0.55) | 3 | 343.64 |
| 5 | 2(1.0s-1) | 2(990℃) | 3(0.85) | 1 | 378.22 |
| 6 | 2(1.0s-1) | 3(1080℃) | 1(0.05) | 2 | 157.83 |
| 7 | 3(0.1s-1) | 1(930℃) | 3(0.85) | 2 | 350.71 |
| 8 | 3(0.1s-1) | 2(990℃) | 1(0.05) | 3 | 203.96 |
| 9 | 3(0.1s-1) | 3(1080℃) | 2(0.55) | 1 | 168.23 |
| K1 | 94.90 | 294.70 | 251.22 | 244.73 | |
| K2 | 293.23 | 218.13 | 183.18 | 190.78 | |
| K3 | 240.97 | 116.93 | 194.69 | 193.58 | |
| R | 198.33 | 177.77 | 68.04 | 53.95 |
根据极差分析的原理可知,极差的大小表明各个因素对实验结果影响的主次,极差最大的因素表明此因素的水平对实验指标的影响最大[12],由表 2的极差值R可知:RA>RB>RC>RD,故影响合金流变应力的影响因素的主次关系:应变速率>变形温度>应变量>其他因素。
2 Ti-22Al-24Nb-0.5Y合金热变形行为 2.1 流变应力分析图 2为Ti-22Al-24Nb-0.5Y合金不同应变速率下的应力-应变曲线,在高温压缩变形的初始阶段,应变硬化占主导作用,使合金流变应力随应变量的增加而迅速增大;随压缩变形的继续进行,软化作用逐步加强,流变应力到达峰值后,动态回复和动态再结晶引起的流变软化作用开始大于加工硬化作用,导致流变应力开始迅速下降,当变形量达到某一定值时,加工硬化与动态软化达到动态平衡,在应力-应变曲线上表现出流变应力随变形量的增加而变化不大。

|
图 2 Ti-22Al-24Nb-0.5Y合金不同变形条件下的应力-应变曲线 (a) =0.001s-1; (b) =0.001s-1; (b) =1.0s-1
Fig. 2 Stress-strain curves of Ti-22Al-24Nb-0.5Y alloy under different deformation conditions (a) =1.0s-1
Fig. 2 Stress-strain curves of Ti-22Al-24Nb-0.5Y alloy under different deformation conditions (a) =0.001s-1; (b) =0.001s-1; (b) =1.0s-1 =1.0s-1
|
从图 2可以看出,当应变速率为0.001s-1,变形温度由900℃上升至1100℃时,峰值应力由291.48MPa下降至38.29MPa,下降了253.19MPa,当应变速率为1.0s-1,变形温度由900℃上升至1100℃时,峰值应力由738.84MPa下降至198.91MPa,下降了539.93MPa,峰值应力下降程度明显不同,表明合金流变应力对温度的影响较敏感;当变形温度为900℃,应变速率由0.001s-1上升至1.0s-1时,峰值应力上升了447.36MPa,当变形温度为1100℃,应变速率由0.001s-1上升至1.0s-1时,峰值应力上升了160.62MPa,峰值应力增加显著,表明合金的流变应力对应变速率的影响也较为敏感;而应变速率处在较低水平时(0.001s-1),有足够的时间完成动态回复或再结晶过程,各个温度下的流变软化均可抵消应变硬化,变形温度对流变应力的影响作用减小;当变形温度为900, 930, 960℃时,合金在达到峰值应力后,迅速进入流变软化状态;流变软化与热效应和温度效应有关,由于钛合金热导率较低,变形热不能及时释放到周围,从而易导致局部的温升引起的流变软化,当变形温度较低和应变速率较高时,变形抗力和单位体积变形功都较大,转化成热能能量较多,且低温时热量不易耗散,因而温升就更显著,此外,由于变形在短时间内完成,所以热量的散失也较少,温度效应就越明显[13-14]。当变形温度越高,应变速率越低时,合金的应力-应变曲线越趋向于稳态流动型,即流变应力在变形过程中变化很小。
2.2 计算变形热合金高温塑性变形过程中的温升效应,是导致流变应力产生差异的主要因素之一,因此,钛合金在热加工过程中的形变热效应不可忽视[15]。利用热模拟试验机进行热压缩实验时,其测得的温度为试样表面温度,但在较高应变速率下进行热压缩时,变形的时间较短,变形热不能及时向周围散失,变形过程中趋近于绝热状态,变形热几乎全部用来升高试样温度,因此本研究采用式(1)计算热压缩过程中的升温。

|
(1) |
式中:ΔT为材料变形时所引起的温升,℃;P为与应变速率有关的热转换系数;C为材料的热容系数,N·mm-2·℃-1,该实验选取热容系数C=4[16]。其中

|
(2) |
参照热压缩实验得到的加热温度下应力-应变曲线,根据式(2)计算得到不同变形条件下所对应的温升值。
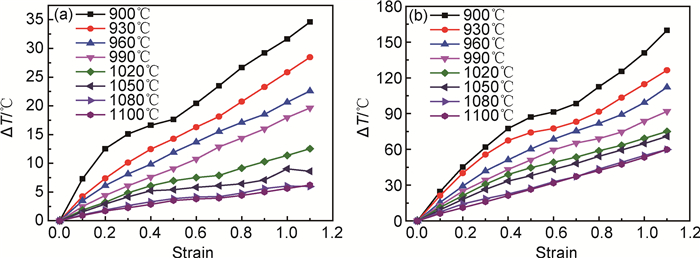
图 3为不同变形条件下的温升曲线,由图 3可见:同一应变速率下,变形热随变形温度的升高而减小;变形热随应变量的增加而增加。当温度为900℃,应变速率为0.001, 1.0s-1时的最大变形热分别为34.59, 159.80℃,变形热之差为125.21℃,表明变形热对应变速率的影响较大,说明变形热是一个不可忽略的参数,图 2中应力-应变曲线在低温高应变速率时的软化程度明显大于高温的软化程度,就是变形热导致的温升所造成的。
|
图 3 Ti-22Al-24Nb-0.5Y合金不同应变速率下的温升曲线 (a)  =0.001s-1; (b) =0.001s-1; (b)  =1.0s-1
Fig. 3 Temperature rise curves of Ti-22Al-24Nb-0.5Y alloy under different strain rates (a) =1.0s-1
Fig. 3 Temperature rise curves of Ti-22Al-24Nb-0.5Y alloy under different strain rates (a)  =0.001s-1; (b) =0.001s-1; (b)  =1.0s-1 =1.0s-1
|
基于正交实验的结果与分析,结合BP神经网络强大的非线性建模能力和各因素对流变应力的影响,建立了一个3层BP神经网络结构(输入层、隐含层、输出层),其中输入层包括3个节点,即形变量、变形温度、应变速率;输出层只有1个节点,即流变应力参数输出;隐含层节点通常是一个较为复杂的问题,如果隐含层节点数量较少,训练出来的网络不够强壮,不能准确识别未参与训练的样本,如果隐含层节点数目较多,会导致学习的时间较长,误差可能达不到最佳,所以有一个最优隐含层节点数存在。隐含层输出节点数的选取参照公式:

|
(3) |
式中:n1为隐含层的节点数;n为输入层的神经元;m为输出层神经元;a为1~10之间的常数。通过反复实验比较发现:具有两个隐含层共8个节点时为最优,最终确定该网络模型结构为3×3×5×1,如图 4所示。

|
图 4 BP神经网络结构 Fig. 4 BP neural network structure |
以Sigmoid函数作为隐含层神经元的激励函数,以Purelin函数作为输出层神经元的激励函数,由输入层至隐含层的第p个训练样本单元j的输出Opj:

|
(4) |
式中:Netj为隐含层第j个神经元的输入;Wij为隐含层和输入层之间的连接权值;Xj为输入层中第j个神经元向隐含层的输出;θj为输入层到隐含层的阈值。
通过对连接权值和各个神经元之间的阈值进行适当的调整,可以完成对复杂的非线性对象进行高精度的建模。如果网络初始阈值被随意进行设定,对于每个输入模式P,网络输出与期望输出存在很大程度上的误差EP,网络训练的误差目标函数E为:

|
(5) |
式中:O′pj为隐含层至输出层的第p个学习样本单元j的网络实际输出;ypj为期望输出;m为训练样本;n为网络输出节点数;Wjk为隐含层到输出层之间的连接权值;θk为隐含层到输出层神经元之间的阈值。
3.2 数据归一化处理将应变速率

|
(6) |
式中:Ni为第i个原始实验数据的归一化值;N′i为原始实验数据;Nmin和Nmax分别表示相对应的输入、输出参数的最小值与最大值。
3.3 神经网络模型训练函数及参数的选择BP神经网络层间传递函数分别选用tansig, purelin,训练函数采用L-M算法(Levenberg-Marquardt)的trainlm函数对BP算法进行优化,比传统的BP及其他改进算法迭代少,精度高,收敛速率快[17]。目标迭代次数设定为1000,目标误差为10-5,学习速率为0.01。
4 结果及分析选取未经训练(应变速率为0.001, 0.1s-1, 变形温度为930, 990, 1080℃)的数据样本,利用BP神经网络建立的合金本构模型的精度进行测试。采用相关系数R 和平均相对误差E,定量描述Ti-22Al-24Nb-0.5Y合金BP神经网络模型的精确度,公式如下:

|
(7) |

|
(8) |
式中:C为实际值;T为预测值;N为数据点个数。将实验值与预测值进行对比,并按照公式(7), (8)计算R与E值。
对比结果如图 5所示,BP预测值偏差在10%以内的数据点占98.79%,模型相关系数R为0.9949,平均相对误差E为3.23%。图 6为Ti-22Al-24Nb-0.5Y合金高温压缩过程中的流变应力的实验值和预测值的比较,通过曲线对比可以看出,流变应力预测值随应变增加而下降的趋势与实际流变应力基本吻合,因此BP神经网络建立的Ti-22Al-24Nb-0.5Y合金本构模型能够较为准确地反映出合金在高温变形过程中的实际情况。

|
图 5 Ti-22Al-24Nb-0.5Y合金流变应力实验值与BP预测值的比较 Fig. 5 Comparision between experimental and BP predicted values of flow stress of Ti-22Al-24Nb-0.5Y alloy |

|
图 6 不同变形条件下BP神经网络本构模型流变应力预测值与实验数据对比 (a)  =0.001s-1; (b) =0.001s-1; (b)  =1.0s-1
Fig. 6 Comparision of BP model predicted value with experimental data of flow stress under different deformation conditions (a) =1.0s-1
Fig. 6 Comparision of BP model predicted value with experimental data of flow stress under different deformation conditions (a)  =0.001s-1; (b) =0.001s-1; (b)  =1.0s-1 =1.0s-1
|
(1) Ti-22Al-24Nb-0.5Y合金在热变形时的流变应力对应变速率和变形温度都较为敏感。随变形温度的升高,流变应力减小;随应变速率的增加,流变应力增大;当应变速率较高,变形温度较低时,合金形变呈流变软化特点,当合金温度较高,应变速率较低时,合金变形呈稳态流动特征。
(2) 基于BP神经网络建立的Ti-22Al-24Nb-0.5Y合金的高温本构关系模型,具有较高的精度,其相关性系数达到0.9949,平均相对误差为3.23%,预测值偏差在10%以内的数据点达到98.79%,能够满足目前工程应用的需要,该预测模型可作为Ti-22Al-24Nb-0.5Y合金塑性成形过程有限元模拟的本构关系。
| [1] | LI S Q, MAO Y, ZHANG J W, et al. Effect of microstructure on tensile properties and fracture behavior of intermetallic Ti2AlNb alloys[J]. Transactions of Nonferrous Metals Society of China, 2002, 12 (4): 582–586. |
| [2] | SHAGIEV M R, GALEYEV R M, VALIAKHMETOV O R, et al. Improved mechanical properties of Ti2AlNb-based intermeta-llic alloys and composites[J]. Advanced Materials Research, 2009, 59 : 105–108. |
| [3] |
沈军, 冯艾寒. Ti2AlNb基合金微观组织调制及热成形研究进展[J].
金属学报, 2013, 49 (11): 1286–1294.
SHEN J, FENG A H. Recent advances on microstructural contr-olling and hot forming of Ti2AlNb-based alloys[J]. Acta Metall-urgica Sinica, 2013, 49 (11): 1286–1294. |
| [4] | YAN J, PAN Q L, LI A D, et al. Flow behavior of Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr alloy during hot compressive deforma-tion based on Arrhenius and ANN models[J]. Transactions of Nonferrous Metals Society of China, 2017, 27 (3): 638–647. DOI: 10.1016/S1003-6326(17)60071-2 |
| [5] |
张麦仓, 罗子健, 曾凡昌. 应用多元非线性回归方法建立FGH95合金的本构关系[J].
材料工程, 1999 (1): 20–22.
ZHANG M C, LUO Z J, ZENG F C. Establishment of constitutive relationship for FGH95 alloy using multiple nonlinear regression method[J]. Journal of Materials Engineering, 1999 (1): 20–22. |
| [6] |
陈慧琴, 林海, 郭灵, 等. TC11钛合金热变形特性分析及其本构关系的建立[J].
材料工程, 2007 (8): 32–36.
CHEN H Q, LIN H, GUO L, et al. Hot deformation charact-eristics and constitutive relation of TC11 alloy[J]. Journal of Materials Engineering, 2007 (8): 32–36. DOI: 10.3969/j.issn.1001-4381.2007.08.008 |
| [7] |
焦李成.
神经网络系统理论[M]. 西安: 西安电子科技大学出版社, 1990.
JIAO L C. Neural network system theory[M]. Xi'an: Xidian University Press, 1990. |
| [8] |
王克鲁, 鲁世强, 李鑫, 等. Ti-6.5Al-3.5Mo-1.5Zr-0.3Si合金本构关系的BP神经网络模型[J].
特种铸造及有色合金, 2008, 28 (8): 575–578.
WANG K L, LU S Q, LI X, et al. A constitutive relation model for the Ti-6.5Al-3.5Mo-1.5Zr-0.3Si alloy based on BP neural network[J]. Special Casting & Nonferrous Alloys, 2008, 28 (8): 575–578. DOI: 10.3870/tzzz.2008.08.001 |
| [9] |
刘雪峰, 马胜军, 刘锦平, 等. Cu-12%Al合金高温压缩变形过程本构关系的BP神经网络模型[J].
材料工程, 2009 (1): 10–14.
LIU X F, MA S J, LIU J P, et al. BP neural networks models for constitutive relationship during high temperature deformation process of Cu-12%Al alloy[J]. Journal of Materials Engineering, 2009 (1): 10–14. DOI: 10.3969/j.issn.1001-4381.2009.01.003 |
| [10] | WANG Z, MAO F, HUANG X P, et al. Orthogonal test design for preparation of TiO2/graphene composites and study on its photocatalytic activity[J]. Rare Metals, 2011, 30 (Suppl 1): 271–275. |
| [11] | JING L J, CUI G W, FENG Q, et al. Orthogonal test design for optimization of the extraction of polysaccharides from Lycium barbarum and evaluation of its anti-athletic fatigue activity[J]. Journal of Medicinal Plants Research, 2009, 3 (5): 433–437. |
| [12] |
杨雄, 刘昌明, 易松林, 等. 水平射流钻头真空扩散焊接工艺正交优化试验[J].
石油天然气学报, 2007, 29 (5): 158–160.
YANG X, LIU C M, YI S L, et al. Orthogonal optimization test of vacuum diffusion welding of horizontally projected jet bits[J]. Journal of Oil and Gas Technology, 2007, 29 (5): 158–160. DOI: 10.3969/j.issn.1000-9752.2007.05.040 |
| [13] |
王克鲁, 鲁世强, 李鑫, 等. 变形温度对TC11合金流动应力及组织的影响[J].
特种铸造及有色合金, 2008, 28 (3): 165–167.
WANG K L, LU S Q, LI X, et al. Effects of temperature on flow stress and microstructure of TC11 alloy at high strain rate[J]. Special Casting & Nonferrous Alloys, 2008, 28 (3): 165–167. DOI: 10.3870/j.issn.1001-2249.2008.03.001 |
| [14] | MURTY S V S N, RAO B N. On the flow localization concepts in the processing maps of titanium alloy Ti-24Al-20Nb[J]. Journal of Materials Processing Technology, 2000, 104 (1/2): 103–109. |
| [15] | ZENG Z P, JONSSON S, ROVEN H J. The effects of defor-mation conditions on microstructure and texture of commercially pure Ti[J]. Acta Materialia, 2009, 57 (19): 5822–5833. DOI: 10.1016/j.actamat.2009.08.016 |
| [16] |
骆俊廷, 陈艺敏, 尹宗美, 等. TA15钛合金热变形应力应变曲线及本构模型[J].
稀有金属材料与工程, 2017, 46 (2): 399–405.
LUO J T, CHEN Y M, YIN Z M, et al. Stress strain curve and constitutive model of TA15 titanium alloy in hot deformation[J]. Rare Metal Materials and Engineering, 2017, 46 (2): 399–405. |
| [17] |
任彦军, 王家伟, 张晓兵, 等. 基于LM算法BP神经网络的高炉-转炉界面铁水温度预报模型[J].
钢铁, 2012, 47 (9): 40–42.
REN Y J, WANG J W, ZHANG X B, et al. Prediction model of hot metal temperature for BF-BOF interface based on LM BP neural network[J]. Iron and Steel, 2012, 47 (9): 40–42. DOI: 10.3969/j.issn.1672-5115.2012.09.014 |
 2019, Vol. 47
2019, Vol. 47


