A100是一种新型高钴镍、二次硬化型超高强度钢，性能接近于美国在1991年研制的AerMet100^[1]。该钢主要通过对合金元素的优化设计，重点突出C, Cr, Mo元素的强化作用，并通过固溶处理、深冷和时效等热处理工艺使得该钢具有高的抗拉强度(1931~2069MPa)和高的断裂韧度(K_IC≥120MPa·m^1/2)的良好配合，主要应用于国产先进战机起落架和各种重要承力构件及防护件^[2-4]。改善材料微观组织结构，提高构件的使用性能是材料进行热加工的重要目标之一。为解决实际热加工生产中存在的问题(如绝热剪切、楔形裂纹以及空洞等组织缺陷)以及提供有限元模拟所需的材料模型，对材料进行等温恒应变速率热压缩实验是研究上述问题的基础。由该实验获得的实验数据可以建立表征材料发生热变形时流变应力与变形温度、应变速率及应变之间的函数关系，即本构关系。宏观唯象本构是最常用的本构关系之一，主要运用数理统计方法搭建流变应力与热力参数之间的函数关系，而不涉及有关原子和分子结构的微观机制，典型代表就是Arrhenius型本构模型^[5-6]。由于本构关系能够客观反映材料在热变形过程中的动态响应特性，因而对材料热变形行为预测、热加工数值模拟及热工艺参数制定等方面具有重要的指导意义。

目前，对超高强度钢热变形本构建模的研究已有大量报道^[7-10]。Ji等^[8]通过Arrhenius型双曲正弦方程和BP神经网络对超高强度钢AerMet100的热变形行为进行了表征，得出BP神经网络在预测流变应力时具有更高的精度；王鑫等^[9]研究了超高强度钢AerMet100的动态再结晶行为，构建了动态再结晶体积分数模型；但上述研究均基于原始数据，并未考虑到实验过程中摩擦和变形热效应对实验数据带来的影响。由于摩擦的存在会导致压缩后试样出现明显的“鼓肚”现象，变形热效应的累积会使实时记录的实验温度升高，这些因素是引起应力误差的主要来源；而现有的热加工模拟试验机均不能消除这些影响，因此有必要对实验数据进行摩擦和温度修正^[11-12]，修正后的数据最接近材料在不同变形条件下的真实热变形行为。

本工作根据Gleeble-3500型热模拟试验机采集的试样压缩数据为基础，采用Ebrahimi等^[13]推导出的有限元法和Laasraoui等^[14]提出的温升公式对原始数据进行摩擦与温度修正及影响分析，并基于修正后的数据经模型推导和回归分析等数学方法确定材料常数(α, n, Q和lnA)与应变之间的分段函数关系，以此构建包含应变的唯象本构模型，用于表征A100超高强度钢的热变形行为，为该钢的实际热成形工艺规范及有限元模拟提供重要依据。

1 实验材料与方法

实验材料为北京航空材料研究院提供的A100超高强度钢锻棒，其主要化学成分(质量分数/%)为：C 0.22, Co 13.81, Ni 11.46, Cr 3.07, Mo 1.2, Fe为余量。热压缩实验在Gleeble-3500型热模拟试验机上进行，实验前须将A100钢锻棒冷加工成直径8mm，高度12mm的小圆柱试样；实验过程中采用真空感应加热，以5℃/s的升温速率加热到系统设定的变形温度(850~1200℃，温度间隔为50℃)，并保温300s使试样温度均匀化，然后以不同的应变速率(0.001, 0.01, 0.1, 1, 10s^-1)进行单向等温恒应变速率热压缩实验，最终成形的压缩量为60%。试样压缩结束后，由设备系统自动处理并保存相关实验数据，同时绘制真应力-应变曲线，以期反映A100超高强度钢的热变形行为。

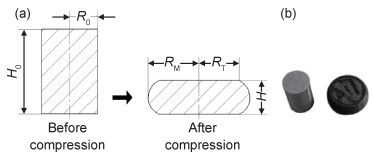
2 结果与分析 2.1 高温流变应力曲线的修正 2.1.1 摩擦修正

图 1为简化的试样压缩示意图和实物图，由实物图(图 1(b))可看到经热压缩后的试样侧面出现明显的鼓形，这是由于试样两端面与压头之间存在不可避免的摩擦力，使得试样在单向热压缩过程中需要额外克服因摩擦力而引起的径向流动阻力，造成变形不均匀，进而导致压缩后的试样出现“鼓肚”现象。该现象的产生需要试样额外做功，也就意味着试样在压缩过程中载荷增大；而大多数的热压缩模拟试验机系统自动采集的载荷-位移数据是以理想压缩状态下(不考虑摩擦的存在)的公式进行真应力-真应变数据的换算，这就导致了实验测定的流变应力值高于真实值。

本工作采用Roebuck等^[15]提出的膨胀系数B这一物理量对单向热压缩实验数据的有效性进行评定，其表达式为：

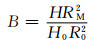
(1)

式中：H, R_M分别为试样形变后的高度和最大“鼓肚”半径；H₀, R₀分别为试样原始高度和半径。

当B < 1.1时，可认为实验数据有效，无须进行摩擦修正；当B≥1.1时，可认为摩擦引起的应力误差较大，应进行必要的摩擦修正。通过对形变后试样的高度和最大“鼓肚”半径进行测量，计算在不同实验条件下的B值，如表 1所示。结果表明计算的B值均大于1.1，说明所获得流变应力数据均需要进行摩擦修正。

根据Ebrahimi等^[13]的结论，采用有限元法推导出来的公式对流变应力实验值进行摩擦修正，即：

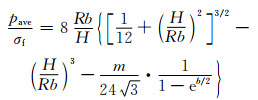
(2)

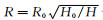
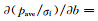
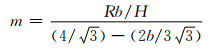
式中：p_ave为实验测得的应力值，MPa；σ_f为摩擦修正后的应力值，MPa；H为试样在任意时刻的高度，mm；R为任意时刻的半径，可由计算，mm；m和b分别为摩擦因子和鼓形参数，可由0计算得出其相应公式，即：

(3)

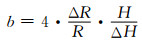
(4)

式中：ΔR=R_M-R_T，mm；R_T为试样压缩后端面与压头的接触面半径，可由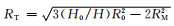计算，mm；ΔH为压缩前、后试样的高度变化，mm；此处的R和H分别为压缩完成后试样的半径和高度，mm。

2.1.2 温度修正

试样在热变形过程中会产生变形热效应，导致试样局部温度的升高，在高应变速率下尤为显著。由于实验温度的记录是由焊接在试样外轮廓表面的热电偶完成，并不能保证试样是在恒温条件下进行压缩成形，这是因为试样在不断压缩过程中，心部累积的温度一时不能转移，导致温度从心部至表面是不均等的。正是由于温升效应的存在，使得实验测定的流变应力并不是某一设定温度下的真实值。为了减少试样压缩过程中温升效应对流变应力造成的影响，须对系统测得的流变应力值进行温度修正，以获得恒温变形条件下的真实值。

根据Laasraoui和Jonas的研究工作^[14]，由变形热效应产生的温升为：

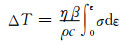
(5)

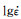
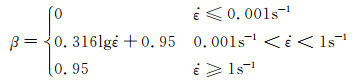
式中：σ为实验值，MPa；ρ和c分别为材料密度(g/cm³)与比热(J·g^-1·K^-1)，根据文献[16]得知该材料的ρ=7.85g/cm³，c=0.465J·g^-1·K^-1；η和β分别为压缩过程中的热转化率与绝热因子，其中钢材的热转化率η一般取0.95，而文献[17]认为绝热因子β在应变速率为0.001~1s^-1范围内与其常用对数成线性函数关系，在不高于0.001s^-1和不低于1s^-1时可分别取0和0.95，即：

(6)

温升ΔT引起的流变应力变化Δσ可按式(7)确定：

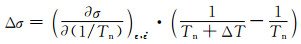
(7)

式中T_n为实验设定的变形温度，K。

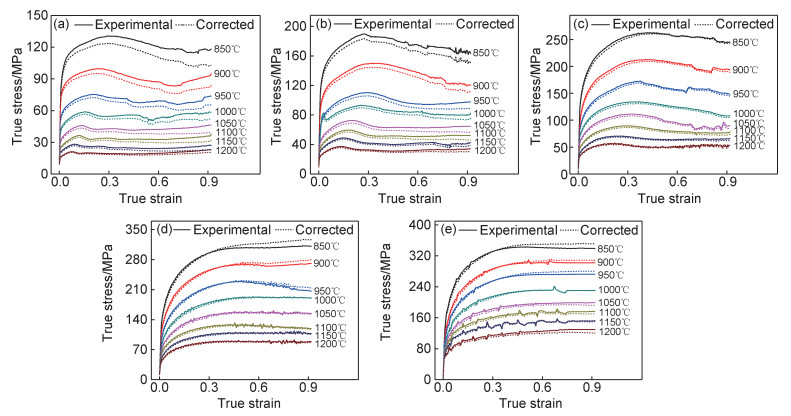
2.1.3 摩擦和温升效应对流变应力的影响

经上述提供的摩擦和温度修正方法，获得了A100超高强度钢在不同应变速率下修正的流变应力曲线，如图 2所示。根据修正前、后的流变应力曲线对比发现，修正后的曲线变化趋势与原始曲线相似，且修正值与实验值之差随应变的增加而增大。

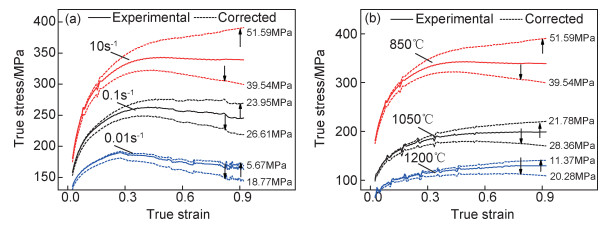
为了进一步研究摩擦和温升效应对流变应力的影响规律，须将摩擦修正的曲线(向下箭头所指)和温度的修正曲线(向上箭头所指)与原始曲线进行比较，如图 3所示。可以看出，当变形温度或应变速率一定时，经摩擦或温度修正后的曲线与原始曲线之间的夹角随应变速率的增加或变形温度的下降而增大(见图 3中修正曲线对应的流变应力差值，该值为实验值与修正值之差的绝对值)，表明摩擦和温升效应对流变应力的影响程度随之变得更加显著。在实验条件下，摩擦和温升效应对流变应力的综合影响效果可通过图 2看出，当修正后的曲线处于原始曲线下方时表明摩擦对流变应力的影响程度高于温升效应，反之低于温升效应；另外，还可看出该钢在变形温度为850~950℃、应变速率为1~10s^-1以及应变高于0.55时的综合修正曲线均在原始曲线上方。这可能是由于材料在低温与高应变速率下易发生绝热剪切、塑性流动失稳等现象，导致材料产生较大的变形热效应，进而引起实验值与修正值之差高于摩擦的影响，使得修正曲线位于原始曲线之上。

2.2 A100超高强度钢唯象本构模型的构建及分析 2.2.1 唯象本构模型的构建

本工作构建的唯象本构模型是基于Sellar和Mctegart提出的Arrhenius型本构模型^[18]，该模型主要用于表征材料热变形过程中高温流变应力与变形温度和应变速率之间的函数关系，用于预测流变应力的双曲正弦函数方程表达式为：

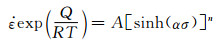
(8)

式中：为应变速率，s^-1；σ为流变应力，MPa；T为变形温度，K；Q为热变形激活能，J/mol；R为气体常数，值为8.314J/(mol·K)。将式(8)中的α, n, Q和A作为材料常数，其中α=β/n₁，可分别由幂函数方程(n₁)和指数方程(β)求解确定。由于材料常数α, n, Q和A的求解是构建预测A100超高强度钢发生热变形时流变应力本构模型的关键。现以ε=0.3条件下对应的修正后的流变应力为例，介绍Arrhenius型本构模型中相关材料常数的求解过程。

首先是材料常数α的确定。在温度一定时，低应力水平(ασ < 0.8)和高应力水平(ασ >1.2)可分别用幂函数方程和指数方程表达，即：

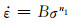
(9)

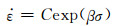
(10)

式中：B和C均是材料常数。

对式(9), (10)两边同时取自然对数，移项得到：

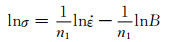
(11)

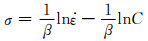
(12)

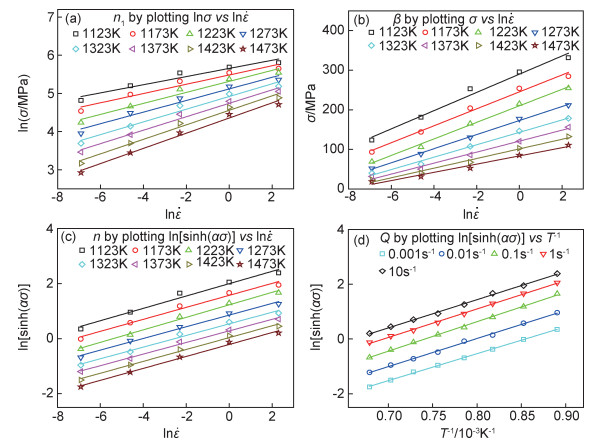
按照式(11), (12)的等式关系，建立lnσ-ln和σ-ln的相关曲线，如图 4(a), (b)所示，可以看出其相关性可用一元线性拟合，由拟合后得到的曲线斜率平均值可计算出n₁=6.37, β=0.059，再根据公式α=β/n₁，便求出α=0.0093。α值的确定是求解其他材料常数的必要条件。

将α值代入式(8)中，对等式两边分别取自然对数，并整理成如下两种形式：

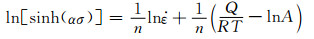
(13)

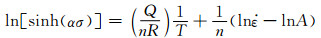
(14)

根据式(13), (14)，建立ln[sinh(ασ)]-ln和ln[sinh(ασ)]-1/T曲线关系图，如图 4(c), (d)所示。由线性拟合后的结果可知，图 4(c)中直线的斜率倒数平均值即为n值；同理，Q和A值可以由图 4(d)中直线斜率S和截距I计算，即Q=nRS，A=exp(ln－nI)。

根据上述的求解流程，在应变为0.3条件下计算的材料常数α=0.0093, n=4.61, Q=395181.88J/mol，A=2.859×10¹⁴。将所求值代入式(8)，便是该应变下对应的本构模型，即：

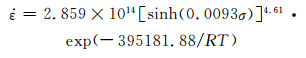
(15)

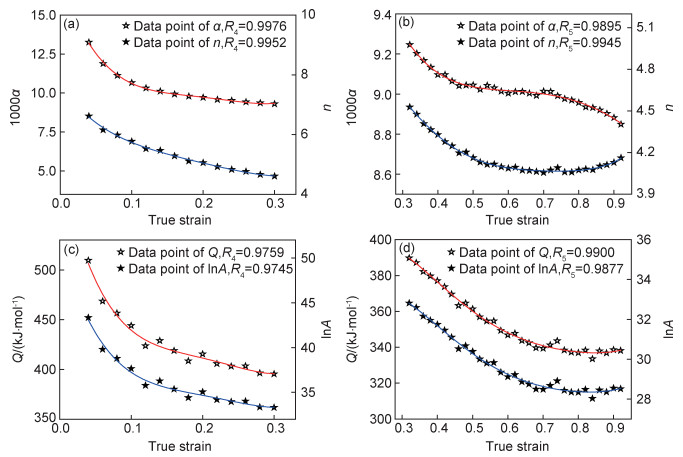
本工作以A100超高强度钢经摩擦和温度修正后的热压缩流变应力为本构建模数据，选取每个压缩实验条件下的应变0.04~0.92(间隔取0.02，共45个应变量)，按照上述的材料常数求解流程，计算相应的α, n, Q和A的值，并采用分段式的多元线性回归拟合方法建立反映材料常数与应变之间的函数关系，以便获得较好的拟合效果。将拟合后含应变的材料常数表达式耦合到Arrhenius型双曲正弦函数方程中，以此表征该钢在不同条件下热变形时流变应力随应变的变化规律。材料常数α, n, Q和lnA与应变的多项式拟合关系曲线如图 5所示，其所确定的分段表达式如下：

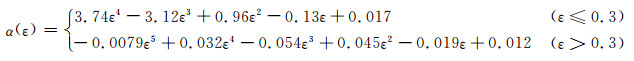
(16)

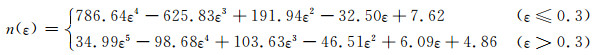
(17)

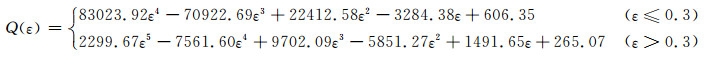
(18)

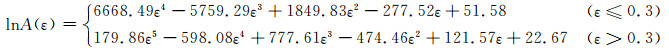
(19)

将分段考虑的材料常数α, n, Q和lnA与应变的函数关系式嵌入到双曲正弦函数方程中，经变换后便得到A100超高强度钢在变形温度为850~1200℃，应变速率为0.001~10s^-1压缩变形的唯象本构模型，其表达式为：

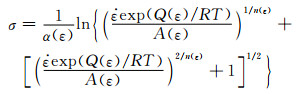
(20)

2.2.2 唯象本构模型的验证及误差分析

图 6为A100超高强度钢在不同实验条件下的实验值与预测值的比较情况。可以看出，本工作建立的唯象本构模型预测结果与大多数的实验数据吻合较好，能基本确定不同实验条件下流变应力曲线的变化趋势。

为了更加准确地描述所建立的本构方程的精确程度，需要对预测数据和实验数据进行误差分析。本工作综合了绝对平均相对误差(δ_AARE)和相关系数R，对本构方程的精确程度进行评定，其相关表达式为：

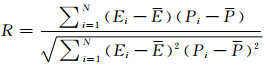
(21)

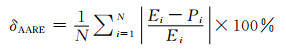
(22)

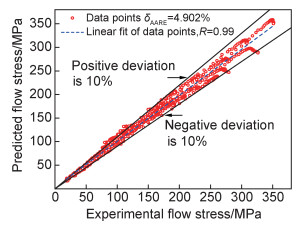
式中：E为实验值；P为预测值；E和P分别代表E和P的平均值；N为分析数据的个数。本工作选取的预测点为1800个，并从两个角度进行误差分析：第一，对单一实验条件下的数据预测效果进行分析，结果如表 2所示；第二，对整个实验数据的预测效果进行相关性分析，结果如图 7所示。由表 2可知，除了950℃, 0.01s^-1条件下的δ_AARE值之外，其余条件下的δ_AARE值均小于10%，比例占97.5%；其中δ_AARE值小于5%的占比为57.5%。另外，根据图 7可知选取的所有预测应力与实验应力的δ_AARE值仅为4.902%，相关系数R值为0.99。综合上述的误差分析结果，说明所建立的唯象本构模型具有良好的预测能力，可用于表征A100超高强度钢的热变形行为。

3 结论

(1) 基于摩擦和温升效应的修正理论，对A100超高强度钢在高温下的流变应力进行了修正，并分析了各因素的影响，结果表明修正前、后的流变应力曲线变化趋势相近，摩擦和温升效应对流变应力的影响随应变速率的增加或变形温度的降低变得更加显著。

(2) 基于Arrhenius型唯象本构模型，采用分段式的多元线性回归拟合方法建立了材料常数(α, n, Q和lnA)与应变之间的函数关系，得到了包含应变量的唯象本构模型，该模型可预测不同应变下的流变应力。

(3) 基于平均相对误差δ_AARE和相关系数R的分析，结果显示构建的唯象本构模型整体预测值的δ_AARE为4.902%，R为0.99，说明该模型具有良好的预测能力。