文章信息
- 梁晓波, 蔡中义, 张曦
- LIANG Xiao-bo, CAI Zhong-yi, ZHANG Xi
- 双向梯形夹芯板柱面弯曲成形回弹分析
- Analysis of springback in cylindrical bending of bi-directional trapezoidal sandwich panels
- 材料工程, 2019, 47(2): 138-145
- Journal of Materials Engineering, 2019, 47(2): 138-145.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2017.001496
-
文章历史
- 收稿日期: 2017-12-05
- 修订日期: 2018-07-01
夹芯板由两块很薄的高强度面板和中间轻质夹芯组成。常见面板材料有金属、纤维铺层、复合材料等,夹芯材料除了传统的蜂窝夹芯、泡沫夹芯,还出现了桁架、梯形等拓扑夹层结构[1-4]。由于夹芯板具有高比强度和比刚度、良好的抗振性能,并能有效地吸收冲击载荷,是航空航天工程中重要的结构材料。随着材料成本不断降低,成形工艺日趋成熟,夹层板的应用已遍及航空、航天、船舶、建筑、交通、风电系统等领域[5-6]。
夹芯板一般为多层异种材料结构,弯曲成形过程比单层材料复杂。石珊珊等[7]通过三点弯曲和面内压缩实验研究了碳纤维/铝蜂窝夹芯结构的Kevlar短纤维界面增韧试件的载荷位移曲线、破坏模式等特征。郑吉良等[8]分析了等腰梯形蜂窝芯玻璃钢夹芯板面外压缩的破坏机理,并研究了夹芯板结构参数对其面外压缩强度的影响及蜂窝芯层数对其面外压缩抗压强度的影响。Katsuhiko等[9]采用线性强化Mises屈服准则描述复合层板面板,研究了复合层板弯曲回弹残余应力分布及回弹量。Corona等[10]研究了钢/聚合物复合层板折弯时钢板的厚度、屈服应力、夹层聚合物剪切模量等参数对复合层板弯曲回弹的影响。Aghchai等[11]分析了铝合金/聚氨酯复合板在不同温度下的弯曲回弹。Liu等[12]提出了结合直梁与曲梁模型解析法预测钢-聚合物夹层板在压边弯曲时的回弹和侧壁卷曲。Yuen[13]通过对拉形过程中各层应力应变关系的研究,推导出多层板回弹的广义解,并提出了简化的封闭形式的解。除解析模型,有限元法也应用在夹层板抗弯性能和回弹的研究[14-15]。目前大部分研究集中于夹芯材料为聚合物的夹层结构,这种夹层结构力学性能受限于胶粘剂,容易发生脱胶和老化。焊接金属夹芯板实现接头的冶金连接,具备更优异的力学性能,然而普通金属夹芯板具有典型的难成形特点,应用多限于平面结构,成形方面的研究较少,严重限制了焊接金属夹芯板的应用潜力。
铝合金-双向梯形夹芯板是一种新型夹芯结构的焊接金属夹芯板,在成形方面有诸多优点,尤其是成形过程中能延缓受压面板屈曲的发生,但对其弯曲成形及回弹的研究还鲜见报道。
本工作采用半解析法[16]获得夹芯等效力学性能参数,分析计算夹芯板在柱面成形过程中面板与夹芯的变形及受力情况,建立夹芯板弯曲回弹的理论分析模型;利用有限元软件ABAQUS分析柱面成形过程面板应力分布及卸载回弹;并应用多点柔性成形技术进行柱面弯曲实验;最后采用建立的模型预测铝合金-双向梯形夹芯板弯曲回弹量,并与数值模拟及实验结果进行对比。
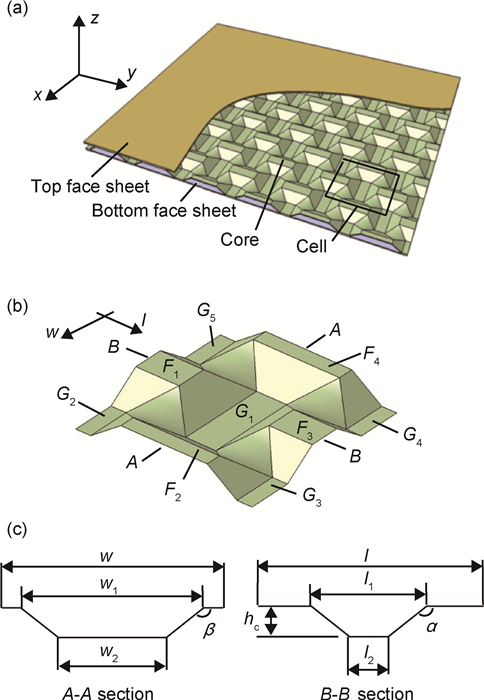
1 双向梯形夹芯板本工作研究的双向梯形夹芯板由上、下面板和双向皆有梯形凸凹波纹的铝合金夹芯通过氮气保护钎焊连接在一起,如图 1(a)所示。上、下面板采用5050-0铝合金板材,夹芯为5083铝合金。图 1(b)为夹芯的胞元,由一个梯形凹台、四个1/4梯形凹台及四个1/2梯形凸台组成,梯形台的各斜平面间通过四边形曲面过渡。四个梯形凸台的上平面F1,F2,F3,F4与上面板焊接,五个梯形凹台的下平面G1,G2,G3,G4,G5与下面板焊接。胞元长度方向记为l方向,宽度方向记为w方向。胞元的主要尺寸参数为:长度l=47mm、宽度w=47mm,梯形凹台在方向的上口宽度l1=24mm、下底宽度l2=8mm,在方向的上口宽度w1=39mm、下底宽度w2=23mm,夹芯相对密度=0.13。图 1所示的坐标轴的z向为夹芯板厚度方向,x向为柱面的轴线方向,y向为柱面弯曲方向。夹芯板胞元的方向与y向一致,胞元的方向与x向一致。夹芯板的面板和芯板的材料力学性能参数如表 1所示。
|
图 1 双向梯形夹芯板及其胞元结构 (a)双向梯形夹芯板; (b)芯板胞元 Fig. 1 Bi-directional trapezoidal sandwich plate and cell structure (a)bi-directional trapezoidal sandwich panel; (b)core cell |
| Type | ρ/ (kg·m-3) |
E/ GPa |
Ep/ GPa |
μ | σs/ MPa |
σb/ MPa |
| 5050-0 | 2800 | 69 | 1.59 | 0.33 | 45 | 147 |
| 5083 | 2720 | 71 | 0.33 | 128 | 361 |
双向梯形夹芯板的夹芯结构复杂,难以通过完全解析法获得等效弹性常数。本工作采用结合有限元的半解析法对夹芯进行等效分析,得到夹芯的等效弹性常数,无须考虑夹芯的复杂结构。
2.1 有限元方法计算等效弹性常数对于正交各向异性板,反对称弯曲变形时,主要承受中面弯矩Mx, My和扭矩Mxy以及横向剪切力Px, Py,弯曲内力与应变分量的关系如下:
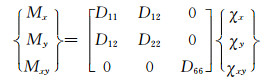
|
(1) |
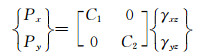
|
(2) |
式中:D11, D22, D12为抗弯刚度;D66为抗扭刚度;C1, C2为剪切刚度。
刚度常数与弹性常数的关系如下:
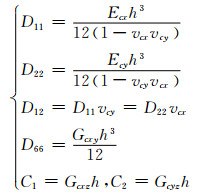
|
(3) |
式中:Ecx,Ecy为x,y方向夹芯的等效弹性模量;vcx,vcy为两个方向的泊松比;Gcxy,Gcxz,Gcyz为不同方向的剪切模量;h为夹芯的高度。
由弹性力学理论可知,式(1),(2)中的应变分量与位移之间的关系如下:
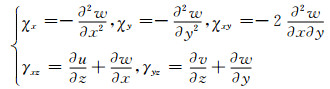
|
(4) |
利用式(4)对夹芯单元各个侧面的节点施加位移来实现不同应变分量的边界条件;从数值模拟结果中提取节点力,通过计算得到5种独立应变下的弯曲内力Mx,My,Mxy,Px和Py;最后利用式(3)得出夹芯的等效弹性常数。
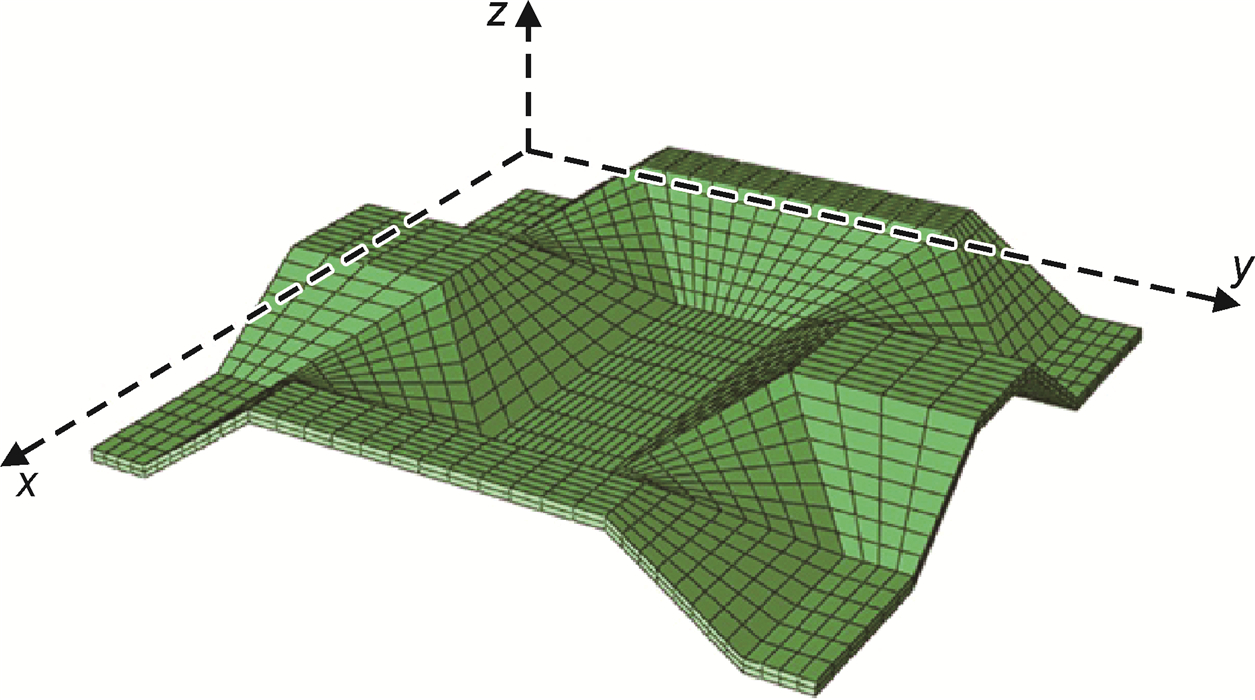
2.2 等效弹性常数的计算过程选取夹芯的一个胞元,使用有限元软件Hypermesh对胞元划分C3D8R实体单元类型。夹芯单元划分的网格如图 2所示。
|
图 2 胞元的网格 Fig. 2 Mesh of core cell |
利用式(4)分别实现5种独立应变边界条件,即应变分量{χx, χy, χxy, γxz, γyz}T只有一个分量不为零,独立应变值取为a,其在弹性变形范围内。
当χx=a时
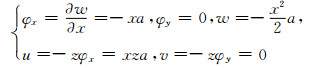
|
(5) |
同理可得χy=a的边界情况。
当χxy=a时
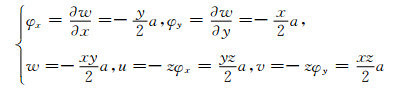
|
(6) |
当γxz=a时
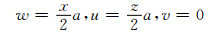
|
(7) |
同理可得γyz=a的边界情况。
另外,为了得到等效泊松比vcx和vcy,再增加一种有限元模型。将εx设为a,可得模型边界上节点的位移自由度的约束情况如式(9),最后利用式(10)得到vcy。
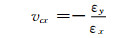
|
(8) |
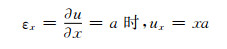
|
(9) |
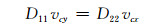
|
(10) |
通过对上述独立应变的有限元模拟,可从结果中提取侧面上节点的节点力(Fx,Fy,Fz),再分别乘以该节点到中面的距离可以得到节点力矩。
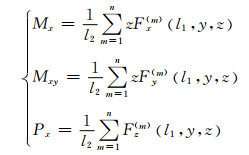
|
(11) |
式中:l1表示单元侧壁的边长;n表示胞元侧面上的节点数;m表示该面上的某一节点。
分别施加5种不同的独立边界条件,联立式(1),(2)和式(3),可得弹性常数的表达式如下:
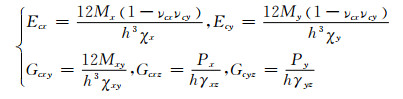
|
(12) |
由于夹芯具有对称结构,将夹芯等效成横观各向同性板。从模拟结果中提取εy,代入式(8)即可得到等效泊松比vcx=0.26;将式(11)得到的Mx, Mxy, Px代入式(12)中计算得到等效弹性模量Ecx=1.56GPa,Gcxy=0.7GPa,Gcxz=0.77GPa。
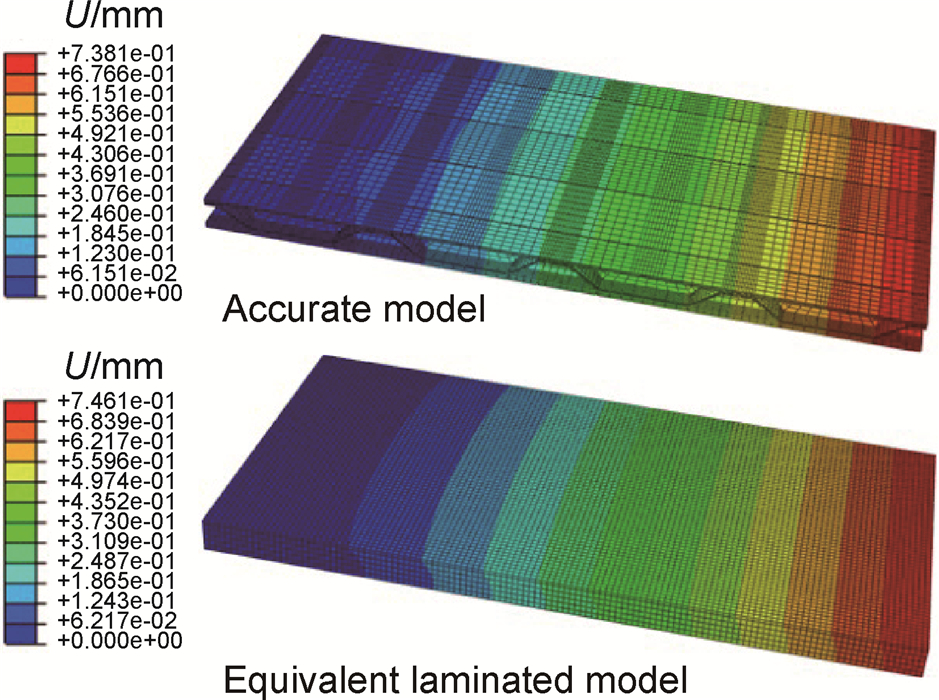
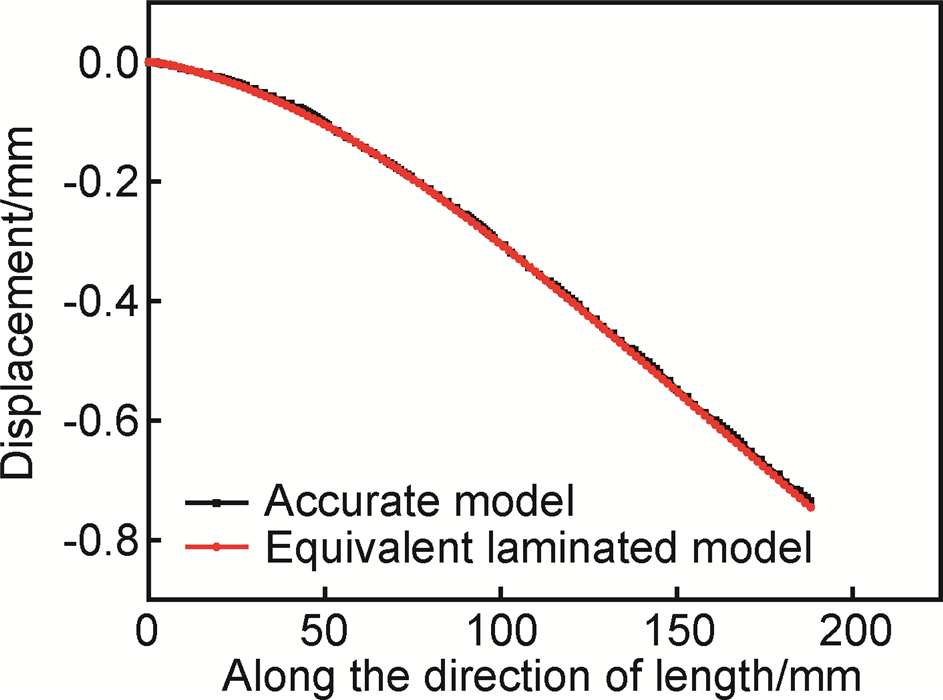
双向梯形夹芯结构的模型为精细有限元模型,等效有限元模型是由上、下面板与等效夹芯组成的三明治夹层板。为验证等效参数的可靠性,通过有限元算例进行分析,取夹芯板的长、宽分别为188mm和94mm,宽度方向一边侧面施加固支约束,上面板表面施加0.01MPa的压强。图 3所示为精细模型与等效模型位移分布云图对比,可看到两种模型最大位移分别为0.738mm和0.746mm,相对误差仅为1.0%。沿长度方向提取上面板中心节点的位移数值,得到如图 4所示的挠度曲线,图中可以看到两种模型挠度曲线基本重合,等效精度较高。
|
图 3 有限元模型位移分布对比 Fig. 3 Comparison of displacement distribution of finite element model |
|
图 4 有限元模型挠度曲线对比 Fig. 4 Comparison of deflection curves of finite element model |
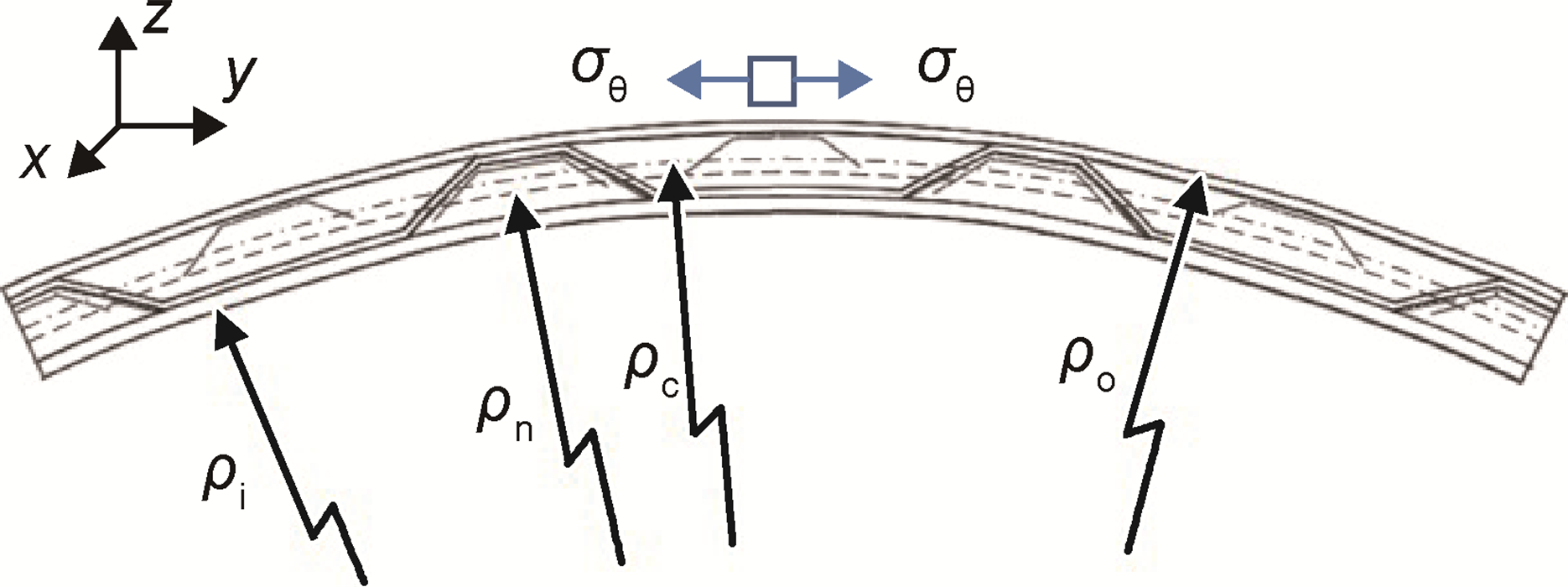
夹芯板弯曲示意如图 5所示。图中ρi, ρo分别为夹芯板的弯曲内径和外径,ρn为应力中性层曲率半径,ρc为夹芯中面半径。为了简化夹芯板弯曲过程的理论分析,本工作对其变形做如下假设。
|
图 5 夹芯板弯曲示意图 Fig. 5 Bending diagram of sandwich panel |
(1) 夹芯板面板宽厚比很大,近似平面应变状态,即面板宽度方向上应变为零,εx=0;
(2) 夹芯板弯曲变形服从Kirchhoff假设;
(3) 夹芯板弯曲过程中各层板料之间无挤压,即厚向应力σr=0;
(4) 夹芯板面板为各向同性等向强化材料,忽略表层铝合金板材变形的“包申格”效应。
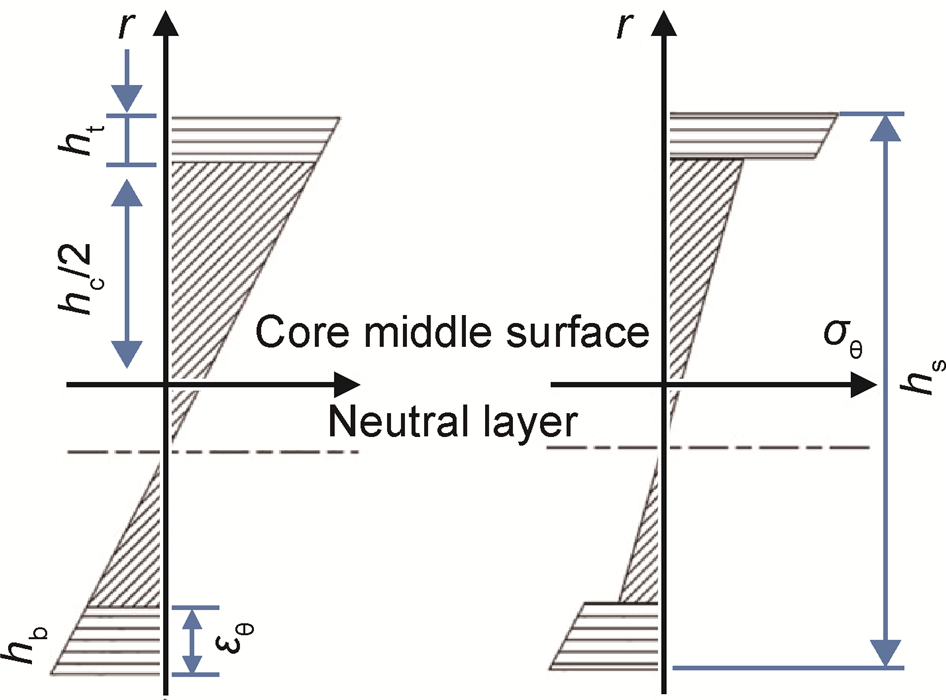
3.1 夹芯板横截面应力计算图 6为夹芯板弯曲横截面应力及应变分布示意图。图中Ai为应力中性层距夹芯中心的距离,hb为下面板厚度,ht为上面板厚度,且hb≥ht,hc为夹芯厚度,hs为夹芯板总厚度,y为任意曲率半径到夹芯中面ρc的距离。
|
图 6 夹芯板弯曲应力-应变分布示意图 Fig. 6 Bending stress and strain distribution schematic diagram of sandwich panels |
根据Kirchhoff假设,夹芯板弯曲截面任意曲率半径ρ处,其切向的线应变为:
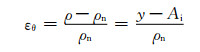
|
(13) |
式中,y=ρ-ρc,ρn=ρc+Ai。
弯曲成形过程中,该夹芯板夹心层较厚且面板较薄,面板发生完全塑性变形。
设面板的塑性变形服从线性应力应变强化关系,由平面应变假设可得到弯曲截面上切向应力应变的关系为:
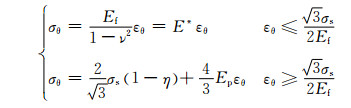
|
(14) |
式中:σs是面板屈服应力;Ep是塑性切线模量;η=Ep/Ef;Ef是面板弹性模量;E*是平面条件下面板弹性模量。
由于中间层夹芯变形一般比较小,且双向梯形夹芯的弹性变形能力远大于面板,由此假设夹芯板弯曲成形及回弹时,夹芯只在弹性范围内变形。处于平面应变状态夹芯的横向应力为
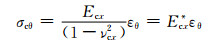
|
(15) |
式中:σcθ是横向应力(MPa);Ecx*是平面应变条件下弹性模量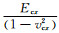
根据外加弯矩在横截面产生的拉应力与压应力合力为零,设加载应力中性层与卸载应力中性层相对于夹芯中心层的z向坐标为A1, A2。
由加载时横截面合力为零,联合式(14)得
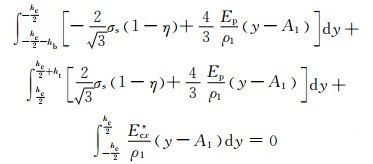
|
(16) |
式中:ρ1是加载应力中性层曲率半径。得到加载时应力中性层z向坐标A1
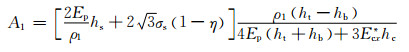
|
(17) |
假设卸载时面板不发生反向屈服,由卸载时横截面合力为零,联合式(14)得
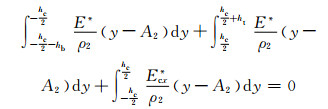
|
(18) |
式中:ρ2是卸载应力中性层曲率半径。得到卸载时应力中性层z向坐标A2
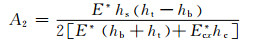
|
(19) |
夹芯板弯曲横截面弯矩及抗弯刚度由上、下面板和夹芯弯矩三部分组成
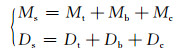
|
(20) |
式中:Ms为夹芯板弯曲成形截面总弯矩;Mt为上面板弯矩;Mb为下面板弯矩;Mc为夹芯弯矩;Ds,Dt, Db, Dc为对应的抗弯刚度。
根据式(17)解得加载应力中性层位置,则下面板加载弯矩为
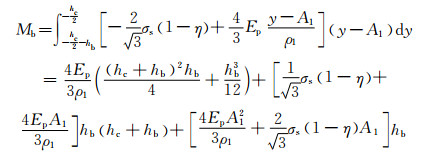
|
(21) |
上面板加载弯矩为
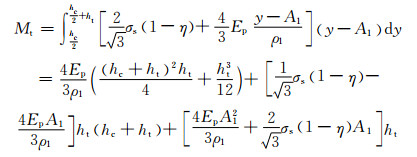
|
(22) |
夹芯加载弯矩为
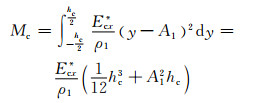
|
(23) |
根据式(19)解得卸载应力中性层位置,则下面板的抗弯刚度为
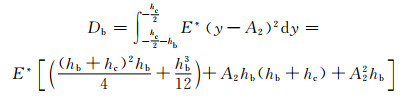
|
(24) |
上面板的抗弯刚度为
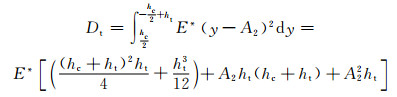
|
(25) |
夹芯的抗弯刚度为
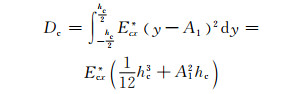
|
(26) |
若卸载不引起反向屈服,且忽略板料卸载过程中的包申格效应,则卸载过程相当于对板料施加一个反向弯矩所引起的弹性变形,利用公式(20)~(26),曲率变化可用下式来表示
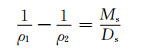
|
(27) |
表 2比较了相同长、宽尺寸下夹芯板的等厚度单层板及等刚度单层板不同柱面成形半径ρ1与卸载回弹后半径ρ2,设回弹比ξ= ρ2-ρ1 /ρ1。夹芯板上、下面板厚度分别为ht=1.0mm和hb=1.5mm,板料尺寸为282mm×94mm。通过计算,等刚度单层板的厚度为7.6mm,其质量是夹芯板的2.3倍;等厚度单层板的质量是夹芯板的2.73倍。从表中可以看出,夹芯板的回弹比略小于等刚度单层板,而略大于等厚度单层板,随着成形曲率半径的增大回弹比逐渐增大,夹芯板回弹量与中厚板十分接近,回弹量较小,易于控制成形精度。
| ρ<1/mm | Sandwich plate | Equal stiffness monolayer | Equal thickness monolayer | |||
| ρ2/mm | ξ/% | ρ2/mm | ξ/% | ρ2/mm | ξ/% | |
| 500 | 573 | 14.6 | 578 | 15.6 | 567 | 13.4 |
| 600 | 701 | 16.8 | 712 | 18.7 | 695 | 15.8 |
| 800 | 975 | 21.9 | 1003 | 25.4 | 969 | 21.1 |
| 1000 | 1272 | 27.2 | 1327 | 32.7 | 1270 | 27.0 |
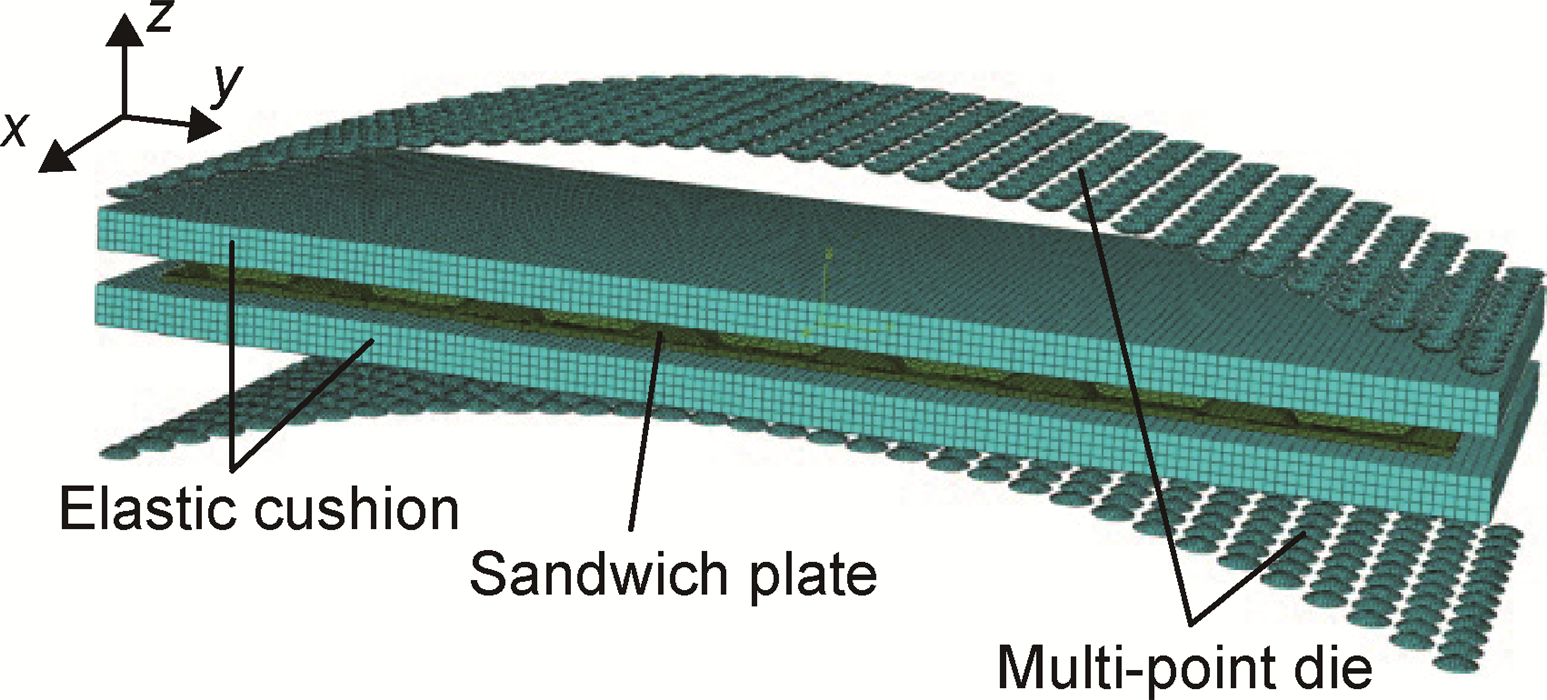
采用有限元软件ABAQUS对夹芯板柱面成形及回弹过程进行数值模拟分析。图 7所示为多点成形模型,由多点模具、弹性垫和夹芯板组成,弹性垫为邵氏硬度A79的聚氨酯,模具采用R3D4壳体单元划分网格,弹性垫和夹芯板采用C3D8R实体单元划分网格,下多点模具完全固定约束,上多点模具以10mm/s的速度下压。
|
图 7 夹芯板柱面成形的有限元模型 Fig. 7 Finite element model of forming sandwich plate cylinder |
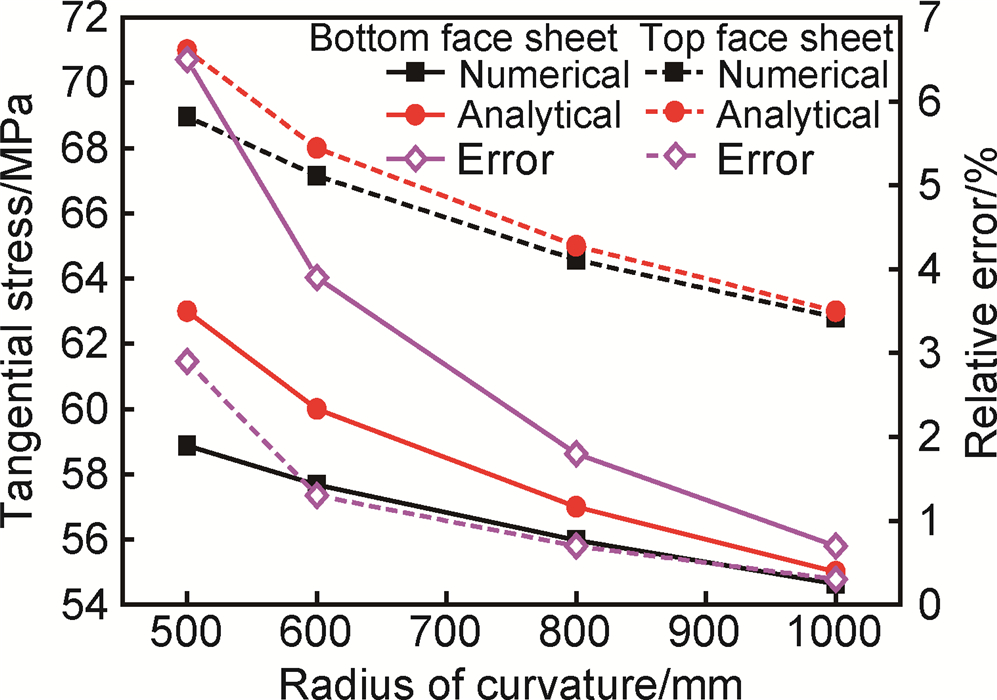
图 8为夹芯板不同成形半径柱面件横截面的面板中心层切向应力模拟值和计算值对比。在柱面弯曲成形过程中,上面板受拉,下面板受压,压应力取绝对值。可以看出,随着曲率半径的增大,上、下面板切向应力计算值和模拟值均逐渐减小;计算得到应力值大于模拟值,这是由于忽略剪切变形等简化假设使得刚度增大造成的;上面板应力相对误差在2.9%以内,下面板应力相对误差在6.5%以内,随着曲率半径的增大误差减小。二者变化规律基本相同,一定程度说明了计算模型的正确性。
|
图 8 不同成形半径柱面件切向应力对比 Fig. 8 Comparison of tangential stress of cylindrical parts with different forming radius |
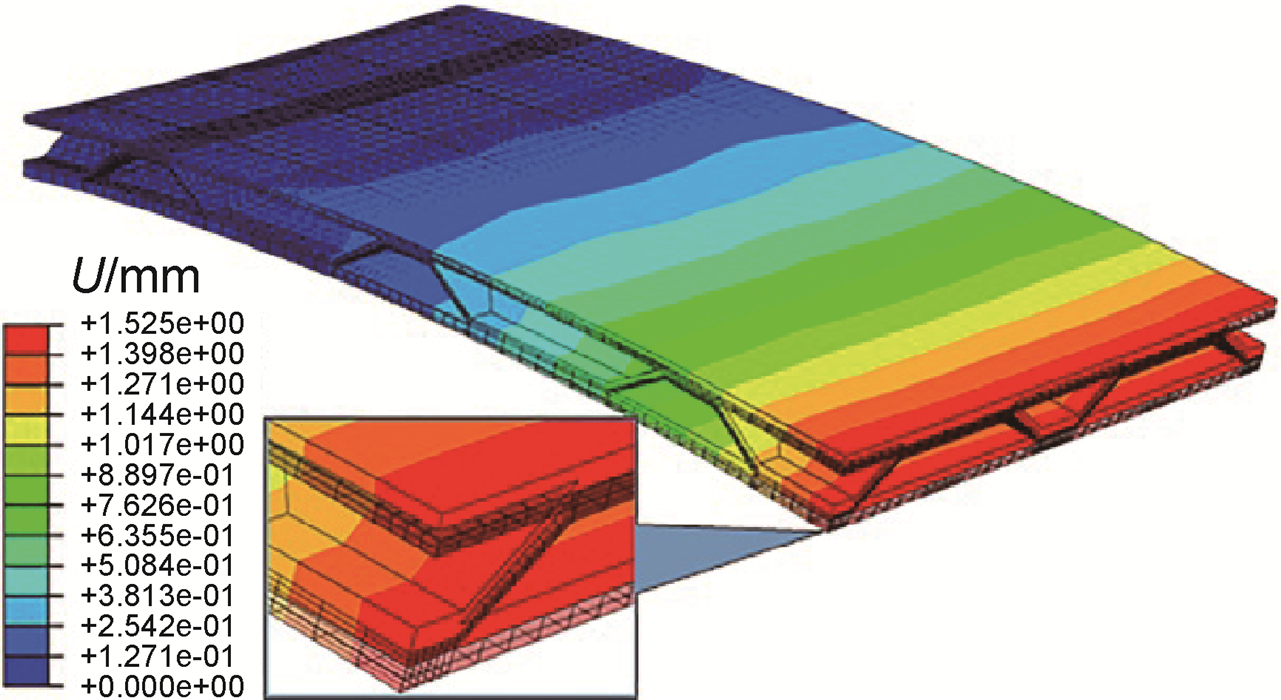
图 9为夹芯板柱面成形后卸载回弹量分布,由于对称截取二分之一进行分析。网格部分显示为回弹前的柱面,色谱面显示的为回弹后的柱面。可以看出,夹芯板柱面件回弹后曲率半径变大,回弹量从中心到边缘均匀增大,而最大回弹量远小于单层薄板。也可观察到双向梯形夹芯板成形件的面板和夹芯都保持很好的平滑度,没有出现面板凹窝、夹芯屈曲及焊接处断裂等缺陷。
|
图 9 夹芯板成形后卸载回弹量分布 Fig. 9 Springback distribution of sandwich panel after unloading |
利用多点成形压机对夹芯板进行柱面成形实验。通过计算机控制系统调整离散基本体高度构成目标模具型面,将夹芯板成形为不同曲率半径的柱面件,图 10为夹芯板柱面件成形实验与扫描,其中图 10(a)为多点压机柱面弯曲成形过程,图 10(b)为成形半径分别为500, 600, 800mm实验件,图 10(c)为PRO-CMM系统三维光学扫描仪。利用三维光学扫描仪对实验件的表面进行扫描得到试验件外形轮廓点云数据。

|
图 10 多点柱面成形及扫描 Fig. 10 Multi-point pressure cylindrical forming and scanning |
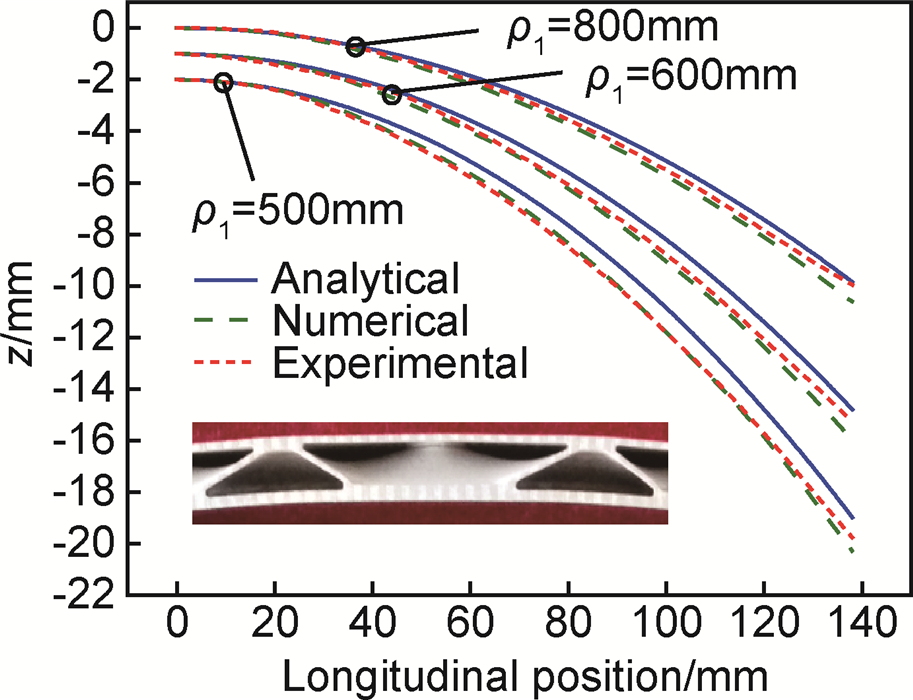
图 11给出了夹芯板不同成形半径柱面件通过计算、模拟及实验得到回弹后的下面板二分之一纵向截面轮廓线对比图。可以看出,不同成形半径柱面件回弹的模拟轮廓线与实验轮廓线基本重合,只在边缘处实验值略大于模拟值,这是由多点模具成形的直边效应导致;计算回弹略微偏大,由于忽略剪切变形等情况造成,与面板应力情形一致;同样可以看到,模拟和实验轮廓线平滑,没有发生凹陷、屈曲等缺陷,图中ρ1=500mm实验件纵向截面局部放大图显示面板和夹芯都没有发生凹陷、屈曲、焊缝断裂等缺陷,与数值模拟一致,表明该种夹芯板具备很好的成形性能。
|
图 11 不同成形半径夹芯板回弹后纵向截面轮廓线 Fig. 11 Longitudinal cross section line of the sandwich plate after springback with different forming radius |
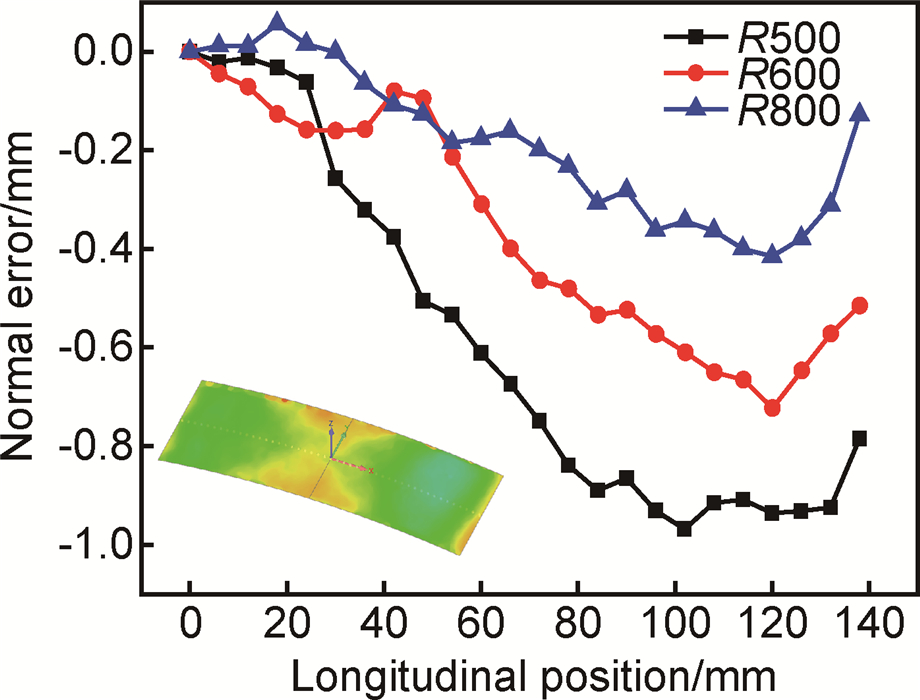
将理论计算值得到的柱面与实验件点云数据导入Geomagic Qualify进行误差分析。图 12给出了夹芯板不同成形半径回弹的计算值与实验值纵向中心截面线误差。可以看出,误差从中心到边缘逐渐增大,只在边缘处由于直边效应有小幅的降低,不同成形半径变化趋势一致;随着成形曲率半径的增大,误差逐渐减小;其中ρ1=500mm时最大误差为0.97mm,ρ1=600mm时最大误差为0.73mm,ρ1=800mm时最大误差为0.42mm,不同成形半径柱面件计算值与实验值的误差均在1.0mm范围内,回弹预测精度较高,说明本工作建立的理论分析模型可以较好地预测双向梯形夹芯板的弯曲回弹。
|
图 12 计算值与实验值纵向截面线误差 Fig. 12 Error along the section line of measured values and analytic values |
(1) 钎焊双向梯形夹芯板的夹芯结构复杂,难以通过完全解析法获得等效弹性常数。采用结合有限元的半解析法对夹芯进行力学参数等效推导,通过对夹芯胞元边界施加位移条件实现弯曲时的独立变量,获得弯曲内力,再由本构关系得到夹芯的等效弹性常数,无须考虑夹芯的复杂结构。
(2) 对上、下面板不等厚的双梯形夹芯板弯曲成形时面板和夹芯的变形特点进行分析,提出合理的简化假设。推导了夹芯板弯曲成形应力中性层的变化,在此基础上建立了夹芯板平面应变弯曲成形回弹的理论计算模型。
(3) 理论计算表明:夹芯板的回弹比略小于等刚度单层板,而略大于等厚度单层板,随着成形曲率半径的增大回弹比逐渐增大,夹芯板回弹量与中厚板十分接近,回弹量较小,易于控制成形精度。
(4) 不同成形半径夹芯板理论解析法计算的应力比数值模拟偏大,从而回弹也偏大,随着成形半径的增大,应力相对误差逐渐减小,其中上面板应力相对误差在2.9%以内,下面板应力相对误差在6.5%以内;计算与实验的下面板纵向中心截面线误差在1.0mm范围内,各项误差均在很小范围内,验证了回弹计算模型的准确性。
| [1] | WELCH D. The sandwich plate system[D]. Glasgow: College of Nautical Studies. 2005. |
| [2] | ZHOU D, STRONGE W J. Mechanical properties of fibrous core sandwich panels[J]. International Journal of Mechanical Sciences, 2005, 47 (4/5): 775–798. |
| [3] | SOROKIN S V. Analysis of wave propagation in sandwich plates with and without heavy fluid loading[J]. Journal of Sound & Vibration, 2004, 271 (3): 1039–1062. |
| [4] | HE M, HU W. A study on composite honeycomb sandwich panel structure[J]. Materials & Design, 2008, 29 (3): 709–713. |
| [5] |
符定梅, 韩静涛, 刘靖, 等. 钢质蜂窝夹芯板的研究进展[J].
航空精密制造技术, 2004, 40 (3): 14–15.
FU D M, HAN J T, LIU J, et al. Progress of study of honeycomb sandwich steel panel[J]. Aviation Precision Manufacturing Technology, 2004, 40 (3): 14–15. DOI: 10.3969/j.issn.1003-5451.2004.03.005 |
| [6] |
王兴业.
夹层结构复合材料设计原理及其应用[M]. 北京: 化学工业出版社, 2007.
WANG X Y. Design principle and application of structural sandwich composite materials[M]. Beijing: Chemical Industry Press, 2007. |
| [7] |
石姗姗, 陈秉智, 陈浩然, 等. Kevlar短纤维增韧碳纤维/铝蜂窝夹芯板三点弯曲与面内压缩性能[J].
复合材料学报, 2017, 34 (9): 1953–1959.
SHI S S, CHEN B Z, CHEN H R, et al. Three-point bending and in-plane compression properties of carbon-fiber/aluminum-honeycomb sandwich panels with short-Kevlar-fiber toughening[J]. Acta Materiae Compositae Sinica, 2017, 34 (9): 1953–1959. |
| [8] |
郑吉良, 彭明军, 孙勇. 等腰梯形蜂窝芯玻璃钢夹芯板的面外压缩性能[J].
材料工程, 2017, 45 (2): 72–79.
ZHENG J L, PENG M J, SUN Y. Out-plane compressive properties for isosceles trapezoid honeycomb core of FRP sandwich panel[J]. Journal of Materials Engineering, 2017, 45 (2): 72–79. |
| [9] | KATSUHIKO I, MASAYUKI K, SUSUMU F. Bending and springback theory of metal-polymer sandwich laminates[J]. Journal of Macromolecular Science Part B, 1981, 19 (4): 773–791. DOI: 10.1080/00222348108246321 |
| [10] | CORONA E, EISENHOUR T. Wiping die bending of laminated steel[J]. International Journal of Mechanical Sciences, 2007, 49 (3): 392–403. DOI: 10.1016/j.ijmecsci.2006.08.007 |
| [11] | AGHCHAI A J, ABOLGHASEMI A, MORADKHANI B, et al. Experimental, theoretical and numerical investigation of springback behavior of Al/composite/Al sandwich sheet[J/OL]. Journal of Sandwich Structures & Materials, 2016, 19(6): doi: 10.1177/1099636216636099. |
| [12] | LIU L, WANG J. Modeling springback of metal-polymer-metal laminates[J]. Journal of Manufacturing Science & Engineering, 2004, 126 (3): 599–604. |
| [13] | YUEN W Y D. A generalised solution for the prediction of springback in laminated strip[J]. Journal of Materials Processing Technology, 1996, 61 (3): 254–264. DOI: 10.1016/0924-0136(95)02182-5 |
| [14] | HUANG Y M, LEU D K. Finite-element simulation of the bending process of steel/polymer/steel laminate sheets[J]. Journal of Materials Processing Technology, 1995, 52 (2/4): 319–337. |
| [15] | LI H, CHEN J, YANG J. Experimental and numerical investigation of laminated steel sheet in V-bending process considering nonlinear visco-elasticity of polymer layer[J]. Journal of Materials Processing Technology, 2012, 212 (1): 36–45. |
| [16] | CHENG Q H, LEE H P, LU C. A numerical analysis approach for evaluating elastic constants of sandwich structures with various cores[J]. Composite Structures, 2006, 74 (2): 226–236. DOI: 10.1016/j.compstruct.2005.04.007 |
 2019, Vol. 47
2019, Vol. 47


