文章信息
- 李凯尚, 彭剑, 彭健
- LI Kai-shang, PENG Jian, PENG Jian
- 预应变对奥氏体不锈钢力学行为的影响及本构模型的构建
- Influence of Pre-strain on Mechanical Behavior of Austenitic Stainless Steel and Construction of Constitutive Models
- 材料工程, 2018, 46(11): 148-154
- Journal of Materials Engineering, 2018, 46(11): 148-154.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2017.000815
-
文章历史
- 收稿日期: 2017-06-30
- 修订日期: 2018-06-09
2. 常州大学 江苏省绿色过程装备重点实验室, 江苏 常州 213164
2. Jiangsu Key Laboratory of Green Process Equipment, Changzhou University, Changzhou 213164, Jiangsu, China
奥氏体不锈钢凭借其良好的力学性能与耐蚀性能,在化工装备、航空航天、机械等领域广泛应用[1],但由于其屈强比低,塑性裕度大,研究人员发现可通过应变强化提高其强度[2]。应变强化的实质是消耗材料的塑性参量提高其强度参数,应变强化同时还会对其他力学性能产生影响,因此对应变强化后的奥氏体不锈钢力学性能开展研究具有重要意义。研究人员针对预应变对材料强度参量、塑性参数和微观组织演变的影响进行了研究[3-7]。毛博文等[3]研究预应变和应变率对HC3400LA合金钢力学性能的影响时发现,应力随着预应变的提高而增加,并且不同预应变量的合金钢延塑性随着应变率的增加而增大;韩豫等[4]研究发现,预应变可提高奥氏体不锈钢的屈服强度,从而减小承压设备壁厚,实现承压装备轻量化;李慧中等[5]研究预变形对Al-Cu-Mn-Mg-Ag合金的组织与力学性能的影响时发现,预应变可以减弱合金时效过程中双阶段时效硬化的现象,同时也会影响合金的屈服强度、抗拉强度和伸长率;Lee等[6]研究发现304L经预应变处理后微观组织发生了明显变化,预应变过程中位错密度、孪晶密度以及马氏体体积分数的增加对压缩流变应力产生影响;吴珞菲等[7]研究预变形对304L焊接组织的影响时发现,304L预应变后焊接获得了更为均匀的接头组织。同时,研究人员从应变速率敏感性、温度敏感性和应变硬化等方面研究材料的力学行为。Choi等[8]研究渗氢处理的316L发现,316L在573~773K时应变速率敏感性指数为负值,并指出在此温度区间内发生了动态应变时效。但是,关于预应变对材料应变速率敏感性、温度敏感性和应变硬化行为的影响鲜有报道。
在众多本构模型中,包括Johnson Cook [9-11], Zerilli-Armstrong [12-13]和Arrhenius [14-17]等主要考虑了温度与应变速率对拉伸行为的影响。但是现有的研究均发现预应变会对力学性能产生显著影响,构建考虑预应变的本构模型是尚待解决的问题。本工作研究预应变对316L不锈钢力学行为的影响,揭示预应变对强度参量、塑性参量、应变速率敏感性、温度敏感性和应变硬化行为的影响规律,并从预应变对材料微观组织的影响出发解释了预应变对力学行为的影响原因,最后基于预应变对拉伸行为的影响规律构建考虑预应变的Modified Johnson Cook(MJC)和Modified Zerilli-Armstrong(MZA)本构模型。
1 实验材料与方法本研究所用316L奥氏体不锈钢的元素含量(质量分数/%):C 0.02, Si 0.42, Mn 1.63, P 0.023, S 0.02, Ni 12.17, Cr 17.23, Mo 2.18, Fe为余量。根据ASTM E8M-04,将316L板材利用线切割制成标准试样,使用1500#砂纸磨光试样表面,保证试样表面具有相同的粗糙度。在AGS-D电子万能材料试验机上于室温下将试样以5×10-4s-1的应变速率进行预应变,预应变量分别为0%(原始态)、5%和10%,然后对试样在不同温度和应变速率下进行拉伸测试,实验温度范围为293~573K,拉伸应变速率范围为0.0005~0.01s-1。
2 结果与分析 2.1 预应变对316L不锈钢拉伸行为的影响图 1是不同预应变量的316L不锈钢强度参量和塑性参数的变化规律(以应变速率0.0005s-1为例)。从图 1(a)中可以看出316L在不同温度下的屈服强度随预应变量明显升高,但是其抗拉强度变化并不显著。在预应变过程中位错开动摆脱溶质原子的钉扎,使原先的柯氏气团消失,并且高密度的可移动位错导致了多系滑移,位错积塞造成了材料的应变强化[3]。研究表明奥氏体不锈钢在预应变的过程中会产生位错塞积,同时机械孪晶也会随着应变量的增加而增加[6, 18-19]。并且还有研究表明应变强化可能会引起应变诱导马氏体的产生,但是这种现象需要在较大的应变强化量(15%以上)时才会出现[18]。由于在本研究中316L不锈钢的预应变量在10%以内,没有产生应变诱导马氏体。因此,通过预应变使316L不锈钢屈服强度提高的原因主要是预应变过程中产生了位错塞积以及机械孪晶组织。从图 1(b)可以看出316L不锈钢的断后伸长率在不同温度下随着预应变量明显降低,由于在应变强化过程中,损耗了部分塑性能量,由此体现出塑性参量随着预应变量的增加而降低,这也充分说明了应变强化是以消耗材料的塑性参数来提高其强度参量。

|
图 1 316L不锈钢基本力学参量随预应变的变化规律 (a)强度参量;(b)塑性参数 Fig. 1 Variation law of basic mechanical parameters of 316L stainless steel with pre-strain (a)strength parameter; (b)plastic parameter |
应变强化除了改变强度参量和塑性参数外,还会对温度敏感性、应变速率敏感性以及应变硬化行为产生影响。应变速率敏感性指数m值是表征应变速率敏感性的一个量化指标,可由式(1)求出[20]:

|
(1) |
式中:σ为流变应力,MPa;
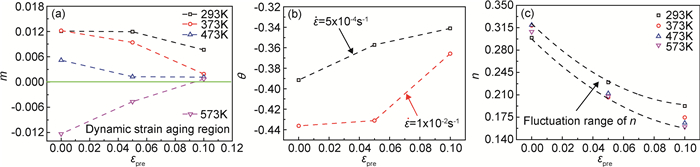
图 2(a)所示为不同温度下316L不锈钢的m值随预应变的变化规律。可以看出,随着温度升高,m由正值逐渐变化为负值,这与中温下316L钢发生动态应变时效有关。Choi等[8]对渗氢处理的316L不锈钢的高温拉伸研究也指出,当温度在573~773K范围时,该材料会出现显著的动态应变时效现象,这与本工作的研究结果一致。从图 2(a)还可以发现无论m是正值还是负值,预应变均会对其产生削弱作用。316L钢的应变速率敏感性现象源于其拉伸行为具有时间相关性,在中低温下拉伸行为的时间相关性与可动位错的滑移有关[21-22]。预应变过程一方面消耗了部分可动位错,另一方面产生的位错塞积以及孪晶组织阻碍了位错的运动。因此预应变会对316L钢的应变速率敏感性产生削弱作用。
|
图 2 316L不锈钢力学性能参量随预应变的变化规律 (a)m值;(b)θ值;(c)n值 Fig. 2 Variation law of mechanical property parameters of 316L stainless steel with pre-strain (a)value of m; (b)value of θ; (c)value of n |
温度敏感性指数θ可由式(2)求出:
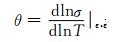
|
(2) |
图 2(b)是316L钢的θ值随预应变的变化规律,可以看出θ均为负值,表现出温度软化现象,同时θ的绝对值会随着预应变量的增加而变弱。随着温度的升高,晶界强度与晶粒强度下降,并且温度的升高还会给位错运动提供能量,使位错更容易在高温下运动, 这些都导致了温度软化。然而在预应变的过程中会产生位错塞积以及孪晶现象,特别是孪晶在随后的中温拉伸过程中难以消失[23]。由于预应变产生的位错塞积以及孪晶会对随后的拉伸过程中的位错运动产生阻碍,同时位错运动又是高温软化现象的原因之一,因此预应变对316L不锈钢的温度敏感性具有削弱的作用。
应变硬化指数n可由式(3)求出:

|
(3) |
图 2(c)表示316L钢的n值随预应变的变化规律,可以看出n值在相同的预应变量下相差不大,需要注意的是n值随着预应变量的增加而降低。这说明316L钢经过预应变后,其抗均匀变形能力降低。预应变过程中产生了位错塞积以及机械孪晶,并且消耗了部分可动位错,这些微观组织的变化会对n值产生显著影响。因此在预应变的过程中消耗了部分抗均匀变形能力,导致预应变后n值降低。
通过上述关于不同预应变下材料的m, θ和n值的分析可知,应变强化对三者都起到了削弱的作用。其原因与在预应变过程中位错塞积的产生和机械孪晶的增加以及可动位错的减少有关。
2.2 构建拉伸本构模型 2.2.1 未考虑预应变影响的MJC模型Lin等提出了一种改进的JC模型[24],能够耦合温度与应变速率的影响,如式(4)所示:

|
(4) |
式中:A1, B1, B2, C1, λ1和λ2是材料常数;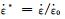
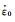
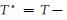
1) 求参数A1, B1和B2。当应变速率为5×10-4s-1,温度为293K时,式(4)可简化为:
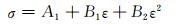
|
(5) |
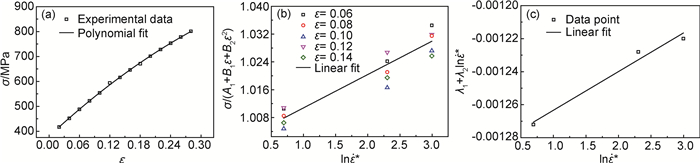
如图 3(a)所示,通过拟合应变速率5×10-4s-1和温度293K下应力-应变曲线,可以获得参数A1, B1和B2,根据图 3(a)拟合数据可得,A1=380.0550MPa, B1=1884.7253MPa, B2=-1373.6264MPa。
2) 求参数C1。当温度为293K时,式(4)可以简化为:
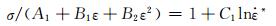
|
(6) |
|
图 3 MJC模型参数的拟合过程  Fig. 3 Fitting process of MJC model parameters
Fig. 3 Fitting process of MJC model parameters  
|
根据式(6)线性拟合温度293K不同应变速率的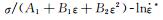
3) 求参数λ1和λ2。将式(4)求对数:
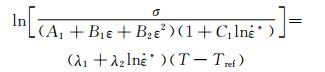
|
(7) |
将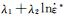
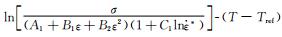
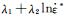
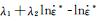
由此可得未考虑预应变影响316L不锈钢的MJC模型:

|
(8) |
ZA模型考虑了位错机制的影响,但未考虑变形条件的影响。Samantaray等提出了一种改进的ZA模型,在预测材料应力应变曲线上得到了很好的应用[25]。MZA模型写成以下形式:

|
(9) |
其中C1, C2, C3, C4, C5, C6和n为材料常数。参考应变速率和参考温度分别取5×10-4s-1和293K。
1) 求参数C1, C2和n。当应变速率为5×10-4s-1,温度为293K时,式(9)可简化为:

|
(10) |
其中C1是应变速率5×10-4s-1和温度293K下的屈服应力,根据应变速率5×10-4s-1和温度293K下的应力与应变值,非线性拟合σ-C1和C2εn曲线,可以获得参数C2和n,根据图 4(a)拟合数据可得,C2=1124.9965MPa,n=0.7042。

|
图 4 MZA模型参数的拟合过程 (a)σ-C1与ε;(b)S1与ε;(c)S2与T* Fig. 4 Fitting process of MZA model parameters (a)σ-C1 and ε; (b)S1 and ε; (c)S2 and T* |
2) 求参数C3和C4。在应变速率为5×10-4s-1时,式(9)可写成:

|
(11) |
线性拟合不同应变量下的lnσ和T*曲线,其斜率S1为-(C3+C4εn);线性拟合S1-ε曲线,其截距是-C3,斜率是-C4。根据图 4(b)可知,C3=-0.0101,C4=0.0109。
3) 求参数C5和C6。式(9)两边取对数可得:

|
(12) |
线性拟合不同温度下的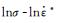
由此可得未考虑预应变影响的316L不锈钢的MZA模型:

|
(13) |
根据MJC和MZA模型可预测未经预应变强化的316L不锈钢在不同温度与应变速率下的应力应变曲线。图 5对比了实验数据和MJC及MZA模型的预测结果,可以发现模型预测数据和实验数据相吻合。式(14)是相关系数R的求解式,R可定量说明本构方程的精确度[26]。

|
(14) |

|
图 5 不同温度下实验值和模型预测值的对比 (a)MJC模型;(b)MZA模型 Fig. 5 Comparison between experimental data and predicted data at different temperatures (a)MJC model; (b)MZA model |
式中:Ei是实验数据;Pi是预测数据;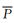
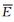

|
图 6 实验值和模型预测值的相关性 (a)MJC模型;(b)MZA模型 Fig. 6 Correlation between experimental data and predicted data (a)MJC model; (b)MZA model |
由2.1节对比不同应变强化量下的316L不锈钢力学行为可以发现,应变强化对材料力学参量会产生显著影响。为了合理表征应变强化材料的力学性能,需要在本构模型中考虑预应变量的影响。应变强化是通过产生永久塑性变形而提高材料的强度,因此为了将预应变量考虑到MJC和MZA模型中,需要将本构模型的应变参量ε与预应变量εpre叠加,由此可将原始材料的拉伸本构模型转化为应变强化材料的本构模型。式(15)为考虑预应变的MJC模型,式(16)为考虑预应变的MZA模型:

|
(15) |

|
(16) |
为了分析考虑应变强化本构模型的合理性,图 7对本构模型得到的应变强化材料的预测结果与实验结果进行比较。从图 7中可发现考虑预应变的本构模型预测结果与不同预应变量316L不锈钢的实验结果基本吻合。图 8所示为考虑预应变强化的MJC和MZA模型预测值与实验值之间的相关性。由图 8可知,考虑预应变的MJC和MZA模型的预测值与实验值具有较好的相关性,相关系数分别为R3=0.9908,R4=0.9946。

|
图 7 考虑应变强化模型的预测值与实验值对比 (a)5%预应变量;(b)10%预应变量 Fig. 7 Comparison between experimental data and predicted data by models considering pre-strain effect (a)5% pre-strain; (b)10% pre-strain |

|
图 8 考虑预应变的本构模型预测值与实验值的相关性 (a)MJC模型;(b)MZA模型 Fig. 8 Correlation between experimental data and predicted data by models considering pre-strain effect (a)MJC model; (b)MZA model |
(1) 316L不锈钢的屈服强度随着预应变量的增加而增大,断后伸长率随着预应变量的增加而减小,但是抗拉强度基本保持不变。
(2) 预应变对316L不锈钢的应变速率敏感性、温度敏感性和应变硬化均会产生影响,应变速率敏感性、温度敏感性和应变硬化行为随着预应变量的增加而被削弱。预应变对316L不锈钢力学性能的影响与预应变过程中位错塞积的产生、机械孪晶的增加以及可动位错的减少有关。
(3) 根据预应变量对316L不锈钢力学行为的影响规律,将预应变强化量考虑到拉伸本构模型中,并构建了考虑预应变的MJC和MZA本构模型;通过改进的本构模型对应变强化316L不锈钢应力应变曲线进行预测,发现预测结果和实验值相吻合。
| [1] | LO K H, SHEK C H, LAI J K L. Recent developments in stainless steels[J]. Materials Science and Engineering R, 2009, 65 (4/6): 39–104. |
| [2] |
郑津洋, 郭阿宾, 缪存坚, 等. 奥氏体不锈钢深冷容器室温应变强化技术[J].
压力容器, 2010, 27 (8): 28–32.
ZHENG J Y, GUO A B, MIAO C J, et al. Cold stretching technique for austenitic stainless steel cryogenic pressure vessels[J]. Pressure Vessel Technology, 2010, 27 (8): 28–32. DOI: 10.3969/j.issn.1001-4837.2010.08.006 |
| [3] |
毛博文, 孙晓屿, 王武荣, 等. 预应变和应变速率对HC340LA低合金高强钢力学性能的影响[J].
塑性工程学报, 2014, 21 (1): 7–12.
MAO B W, SUN X Y, WANG W R, et al. Effect of pre-strain and strain rate on mechanical properties of HC340LA high strength low alloy steel[J]. Journal of Plasticity Engineering, 2014, 21 (1): 7–12. DOI: 10.3969/j.issn.1007-2012.2014.01.002 |
| [4] |
韩豫, 陈学东, 刘全坤, 等. 应变强化奥氏体不锈钢力学行为研究及应用[J].
中国机械工程, 2011, 22 (21): 2633–2637.
HAN Y, CHEN X D, LIU Q K, et al. Study and application on mechanical behavior of austenitic stainless steels based on cold stretching technology[J]. China Mechanical Engineering, 2011, 22 (21): 2633–2637. |
| [5] |
李慧中, 李洲, 梁霄鹏, 等. 预变形对Al-Cu-Mn-Mg-Ag合金的组织与力学性能的影响[J].
航空材料学报, 2009, 29 (2): 29–33.
LI H Z, LI Z, LIANG X P, et al. Effect of predeformation on microstructures and mechanical properties of Al-Cu-Mn-Mg-Ag aluminum alloy[J]. Journal of Aeronautical Materials, 2009, 29 (2): 29–33. |
| [6] | LEE W S, LIN C F, CHEN T H, et al. High temperature microstructural evolution of 304L stainless steel as function of pre-strain and strain rate[J]. Materials Science and Engineering:A, 2010, 527 (13/14): 3127–3137. |
| [7] |
吴珞菲, 成强, 李铸国. 预变形对304L焊接组织的影响[J].
材料工程, 2017, 45 (1): 7–13.
WU L F, CHENG Q, LI Z G. Effect of prior deformation on welding microstructure of steel 304L[J]. Journal of Materials Engineering, 2017, 45 (1): 7–13. DOI: 10.3969/j.issn.1673-1433.2017.01.004 |
| [8] | CHOI M, HOU J, MÁTHIS K, et al. Tensile behavior of hydrogen-charged 316L stainless steel at elevated temperatures[J]. Materials Science and Engineering:A, 2014, 595 (5): 165–172. |
| [9] | HE A, XIE G L, ZHANG H L, et al. A comparative study on Johnson-Cook, modified Johnson-Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel[J]. Materials & Design, 2013, 52 : 677–685. |
| [10] | LIN Y C, CHEN X M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working[J]. Materials & Design, 2011, 32 (4): 1733–1759. |
| [11] | ZHANG D N, SHANGGUAN Q Q, XIE C J, et al. A modified Johnson-Cook model of dynamic tensile behaviors for 7075-T6 aluminum alloy[J]. Journal of Alloys and Compounds, 2015, 619 : 186–194. DOI: 10.1016/j.jallcom.2014.09.002 |
| [12] | LI H Y, WANG X F, WEI D D, et al. A comparative study on modified Zerilli-Armstrong, Arrhenius-type and artificial neural network models to predict high-temperature deformation behavior in T24 steel[J]. Materials Science and Engineering:A, 2012, 536 (1): 216–222. |
| [13] | HE A, XIE G L, ZHANG H L, et al. A modified Zerilli-Armstrong constitutive model to predict hot deformation behavior of 20CrMo alloy steel[J]. Materials & Design, 2014, 56 : 122–127. |
| [14] | PENG J, ZHOU C Y, DAI Q, et al. An improved constitutive description of tensile behavior for CP-Ti at ambient and intermediate temperatures[J]. Materials & Design, 2013, 50 : 968–976. |
| [15] |
张施琦, 冯定, 张跃, 等. 新型超高强度热冲压用钢的热变形行为及本构关系[J].
材料工程, 2016, 44 (5): 15–21.
ZHANG S Q, FENG D, ZHANG Y, et al. Hot deformation behavior and constitutive model of advanced ultra-high strength hot stamping steel[J]. Journal of Materials Engineering, 2016, 44 (5): 15–21. DOI: 10.3969/j.issn.1673-1433.2016.05.004 |
| [16] |
王进, 褚忠, 张琦. 38MnVS6非调质钢两种高温本构模型的对比[J].
材料工程, 2014 (2): 81–86.
WANG J, CHU Z, ZHANG Q. A comparative study of two high-temperature constitutive models of 38MnVS6 microalloyed forging steel[J]. Journal of Materials Engineering, 2014 (2): 81–86. DOI: 10.3969/j.issn.1001-4381.2014.02.016 |
| [17] | PENG J, LI K S, PENG J, et al. The effect of pre-strain on tensile behaviour of 316L austenitic stainless steel[J]. Materials Science and Technology, 2018, 34 (5): 547–560. DOI: 10.1080/02670836.2017.1421735 |
| [18] | PENG Y, GONG J, JIANG Y, et al. The effect of plastic pre-strain on low-temperature surface carburization of AISI 304 austenitic stainless steel[J]. Surface and Coatings Technology, 2016, 304 : 16–22. DOI: 10.1016/j.surfcoat.2016.05.047 |
| [19] | JI H, PARK I J, LEE S M, et al. The effect of pre-strain on hydrogen embrittlement in 310S stainless steel[J]. Journal of Alloys and Compounds, 2014, 598 : 205–212. DOI: 10.1016/j.jallcom.2014.02.038 |
| [20] | JONAS J J, SELLARS C M, TEGART W J M. Strength and structure under hot-working conditions[J]. International Materials Reviews, 1969, 14 (1): 1–24. DOI: 10.1179/095066069790138056 |
| [21] | WANG S H, ZHANG Y, CHEN W. Room temperature creep and strain-rate-dependent stress-strain behavior of pipeline steels[J]. Journal of Materials Science, 2001, 36 (8): 1931–1938. DOI: 10.1023/A:1017545907676 |
| [22] | NEERAJ T, HOU D H, DAEHN G S, et al. Phenomenological and microstructural analysis of room temperature creep in titanium alloys[J]. Acta Materialia, 2000, 48 (6): 1225–1238. DOI: 10.1016/S1359-6454(99)00426-7 |
| [23] | KAMEYAMA T, MATSUNAGA T, SATO E, et al. Suppression of ambient-temperature creep in CP-Ti by cold-rolling[J]. Materials Science and Engineering:A, 2009, 510/511 : 364–367. DOI: 10.1016/j.msea.2008.08.046 |
| [24] | LIN Y C, CHEN X M, LIU G. A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel[J]. Materials Science and Engineering:A, 2010, 527 (26): 6980–6986. DOI: 10.1016/j.msea.2010.07.061 |
| [25] | SAMANTARAY D, MANDAL S, BORAH U, et al. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel[J]. Materials Science and Engineering:A, 2009, 526 (1/2): 1–6. |
| [26] | ROKNI M R, ZAREI-HANZAKI A, ROOSTAEI A A, et al. Constitutive base analysis of a 7075 aluminum alloy during hot compression testing[J]. Materials & Design, 2011, 32 (10): 4955–4960. |
 2018, Vol. 46
2018, Vol. 46


