文章信息
- 丁智平, 黄达勇, 荣继刚, 黄友剑, 曾家兴
- DING Zhi-ping, HUANG Da-yong, RONG Ji-gang, HUANG You-jian, ZENG Jia-xing
- 长玻纤增强复合材料注塑成型构件强度分析
- Strength Analysis of Long Glass Fiber Reinforced Composite Injection Molding Components
- 材料工程, 2018, 46(4): 111-119
- Journal of Materials Engineering, 2018, 46(4): 111-119.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2016.001370
-
文章历史
- 收稿日期: 2016-11-18
- 修订日期: 2017-09-20
2. 株洲时代新材料科技股份有限公司, 湖南 株洲 412007
2. Zhuzhou Times New Material Technology Co., Ltd., Zhuzhou 412007, Hunan, China
随着生态环境日益恶化,为实现节能减排、低碳环保,各国都提出了相应的措施,轻量化技术被认为是目前行之有效的方法和手段[1-2]。纤维增强复合材料是一种纤维增强的高分子材料,具有高比强度、高比模量等特点,是替代金属的轻量化材料[2-3]。
纤维增强复合材料的力学性能除了受基体材料和纤维材料的物理属性影响外,还与纤维的体积分数、纤维长径比及纤维排列方式等有关[4-7]。Eshelby的等效夹杂理论[8],自洽法[9], Mori-Tanaka方法[10]等能对纤维增强复合材料的模量进行预测。基于Jeffery方程[11],Folgar等[12]针对浓缩的纤维悬浮液,考虑流体和纤维的相互作用,给出了纤维角速度模型。在此基础上Wang等[13]基于保持特征值的旋转速率不变的情况下, 通过标量闭合因子降低取向张量特征值的增长速率的理念,提出了RSC取向模型。随后,Phelps等[14]用各向异性旋转扩散(ARD)张量项取代RSC模型中的各向同性标量项,提出了ARD-RSC取向模型,它能有效预测较长纤维间相互作用增强后的纤维取向分布。
纤维增强复合材料由于其注塑结构件的可设计性,应用日益广泛,但因其在注塑成型过程中纤维取向的分散性而影响注塑件的力学性能和使用性能。如何准确预测塑件力学性能,对纤维增强复合材料实际应用十分重要。目前,在工程应用中,一般是将长玻纤增强复合材料作为各向同性材料处理,鲜有考虑其各向异性特征,即在不同的方向抵抗变形及失效的能力不同的特点的分析。针对长玻纤复合材料注塑结构件成型过程中,纤维含量是可控因素,在纤维含量一定的情况下,纤维取向状态是影响长玻纤增强复合材料力学性能的主要影响因素。本工作基于广义牛顿流体本构方程,采用ARD-RSC纤维取向模型,考虑纤维间相互作用,应用数值模拟预测注塑件的纤维取向分布;基于复合材料细观力学的Eshelby夹杂理论,应用Mean Field均匀化方法,建立长玻纤增强复合材料均质化RVE模型;综合运用材料建模、离散均质化RVE模型场、注塑成型和结构有限元分析技术,对构件强度进行分析,并在此基础上针对纤维取向分布不理想对产品力学性能产生重大影响进行结构改进。
1 本构关系和纤维取向模型 1.1 正交各向异性材料弹性本构关系将长玻纤增强复合材料简化为正交各向异性材料,则存在以下应力-应变关系[15]:
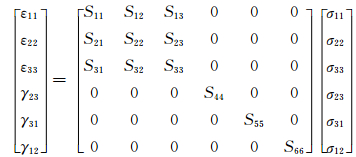
|
(1) |
用矩阵符号表示为:
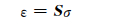
|
(2) |
其中,Sij为柔度系数,S为柔度矩阵,柔度矩阵是刚度矩阵的逆矩阵;同样,Sij具有对称性,只有9个独立柔度系数,刚度和柔度系数对均质材料都可以认为是弹性常数。
正交各向异性材料的柔度矩阵S与9个弹性常数的关系如式(3)所示:
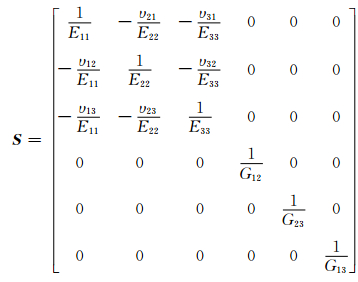
|
(3) |
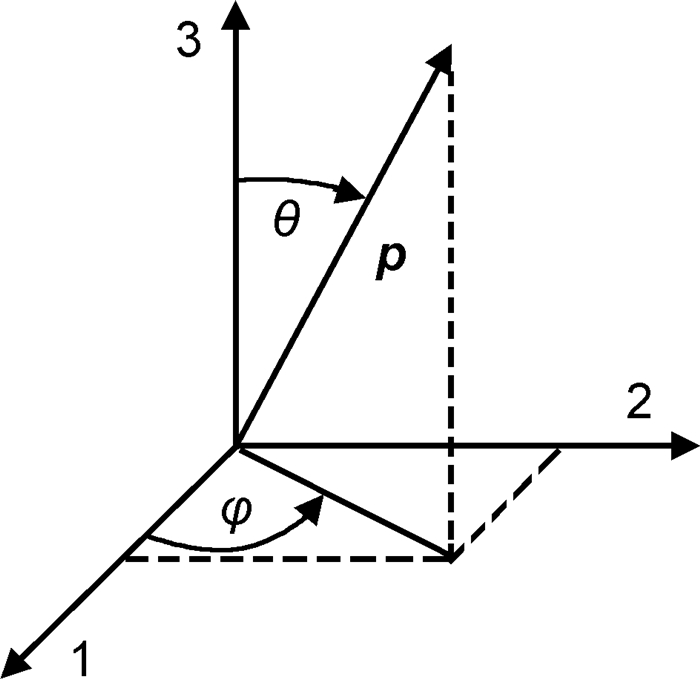
Bay等对纤维取向理论模型[16]进行了研究。在长玻纤增强PA66复合材料中,纤维一般假设为不可弯曲的棒状体,则可用单位矢量p来描述单根纤维的取向,如图 1所示:
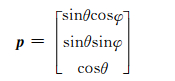
|
(4) |
|
图 1 纤维取向矢量 Fig. 1 Fiber orientation vector |
式中:p为纤维的方向;θ表示p与坐标轴3的夹角;φ表示p在1-2平面上的投影与坐标轴1的夹角。
一组纤维的取向状态可以用概率分布函数ψ(p)表示。假定纤维在流体中流动,该分布函数的守恒方程[17]为:
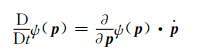
|
(5) |
式中: 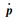
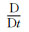
对于长玻纤增强PA66复合材料,纤维分布具有随机性。而对于某一特定区域内分纤维取向分布情况,可用单根特定长度的纤维在空间随机取向状态来描述,即用纤维取向张量描述纤维取向状态。定义单位矢量p的张量积在所有方向上的积分并点乘纤维分布函数ψ(p):
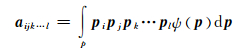
|
(6) |
其中,
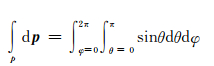
|
(7) |
式中:aijk…l为纤维的取向张量; pi, pj, pk…pl为第i, j, k…l根纤维的方向;分布函数Ω(p)为纤维出现在θ与θ+dθ,φ与φ+dφ之间的概率。
由于纤维随流场一起运动的过程中没有头与尾的区别,则分布函数ψ(p)是偶函数,即ψ(p)=ψ(-p),则奇数个p相乘的积分结果均为0。所以可以只用偶数个p取向矢量的张量积来定义取向张量。现以二阶张量为例,aij=〈pi, pj〉是一个二阶对称张量[16]。二阶张量aij描述纤维取向状态[16]由纤维分布函数定义为:
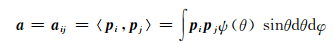
|
(8) |
根据取向张量满足对称性及常规条件αij=αji,二阶取向张量可写成:
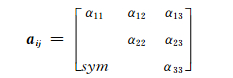
|
(9) |
经对角化后,描述纤维取向状态采用如下二阶张量的形式:
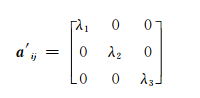
|
(10) |
其中[16],
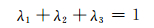
|
(11) |
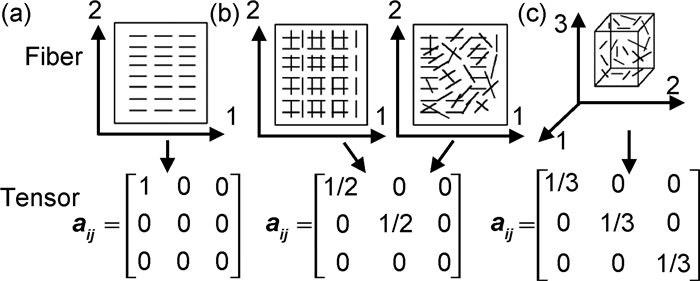
经对角化后的二阶取向张量状态描述,如图 2所示。图 2(a)表示单轴取向,即纤维沿单一方向排列;图 2(b)表示双轴取向,既纤维沿2个主轴方向平均分布,同时也可表示纤维在平面中呈随机取向分布;图 2(c)表示沿3个主轴方向的分布状态或是空间中的随机取向。
|
图 2 纤维取向张量 (a)单轴取向; (b)二维随机取向;(c)3D随机取向 Fig. 2 Fiber orientation tensor (a)uniaxial aligned; (b)planar random biaxial; (c)3D random |
进行注塑成型流动模拟,假设忽略熔体弹性,可采用广义牛顿流体本构方程[18]:
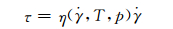
|
(12) |
式中:τ为剪切应力, Pa; η(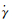
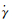
在注塑成型加工数值模拟中,利用取向分布函数能完整描述纤维取向状态,但需要巨大的计算资源,目前多使用取向张量来描述纤维取向。在Folgar-Tucker模型[12]和RSC模型[13]的基础上,Phelps等[14]用各向异性旋转扩散(ARD)张量项取代RSC模型中的各向同性标量项,提出了ARD-RSC取向模型,它能有效预测较长纤维间相互作用增强后的纤维取向分布,演化而成的ARD-RSC模型方程如下所示:
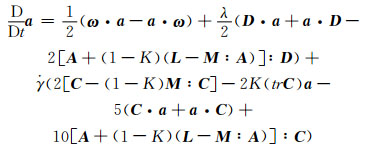
|
(13) |
其中,
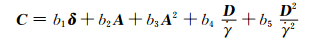
|
(14) |
式中:σP,eiP分别为取向张量a的Pth特征值以及Pth特征值ith分量,四阶张量L和M定义如下:
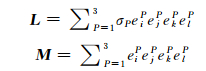
|
(15) |
式中:a, A分别为二阶、四阶纤维取向张量,D为变形速率张量, ω为涡动张量,λ为纤维几何形状因子,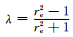
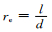
基于Eshelby等效夹杂理论[8],Mori-Tanaka方法[10]假设复合材料的体积平均应力应等于其远场作用的均匀应力,其等效弹性模量为:
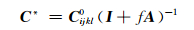
|
(16) |
其中,
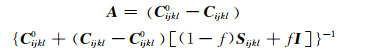
|
(17) |
式中: Cijkl0为基体弹性张量; Cijkl为夹杂体弹性张量; Sijkl为Eshelby张量; I是四阶单位张量;f是夹杂相体积比。
复合材料至少由两种材料构成,因此在微观上,由于微观结构的不均匀性,其应力和应变也将不再是均匀的。复合材料在某个方向的模量和强度是用实验测量得到的宏观整体平均的应力σ-应变ε值的关系来求得的,即
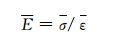
|
(18) |
假设存在一种均质材料,该材料在某一方向上的应力-应变关系与复合材料在同一方向的应力-应变关系一致,同样具有杨氏模量E,则可以用这个均匀材料来代替非均匀材料在该方向上的力学性能。
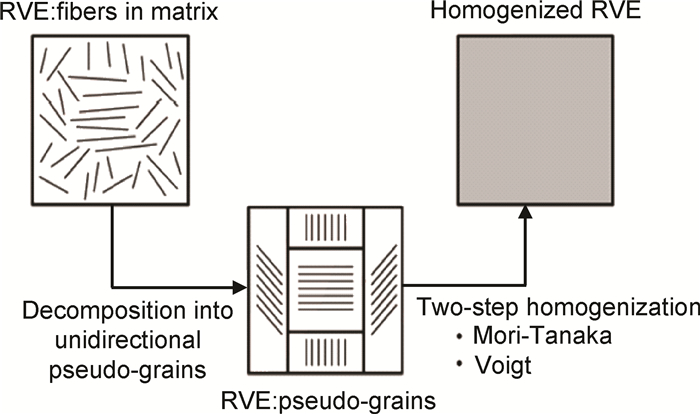
为了有效预测纤维增强复合材料宏观力学响应,建立细观纤维均质化RVE模型如图 3所示。首先根据Mori-Tanaka模型对每一个伪谷粒均质化,然后使用Voigt模型[7]对所有伪谷粒进行集体均质化计算。
|
图 3 纤维均质化RVE模型 Fig. 3 Fiber homogenized RVE model |
汽车推力杆主要用于保持车桥位置的相对固定,保证车轮和车身之间有确定的运动关系,使汽车具有良好的驾驶性能。推力杆中装有橡胶球铰,在汽车行驶过程中,橡胶球铰频繁受到拉压,为提高球铰寿命,在安装球铰时,要使球铰处于预压状态。推力杆的材料为热塑性长玻纤增强PA66(GF50)复合材料,由PA66尼龙树脂基体和玻璃纤维增强相两部分组成,两相均为各向同性材料,其力学性能见表 1。
| Material | Density/(g·cm-3) | Tensile modulus/MPa | Tensile strength/MPa | Poisson’s ratio |
| PA66 | 1.14 | 3 | 70 | 0.39 |
| E-glass | 2.54 | 72 | 3600 | 0.22 |
参照GB/T 1447-2005纤维增强塑料拉伸性能实验方法,使用长玻纤增强PA66(GF50)复合材料I型注塑拉伸试样,在JYW-93 Z100高低温电子万能材料试验机上进行拉伸实验,加载速率为2mm/min,测试试样为5根,5组数据获取的拉伸模量和泊松比见表 2。试样的纤维长度方向与拉伸方向一致,表中的拉伸强度是表征其近似纤维长度分布方向的强度。
| Material | Tensile strength/MPa | Tensile modulus/MPa | Poisson’s ratio |
| PA66(GF50) | 205 | 16800 | 0.33 |
杆体设计质量为2kg,为了节省开发费用,作者选取二分之一模型进行注塑加工,如图 4所示,质量为1kg。在实际注塑成型加工中,杆体质量范围0.8~0.93kg。

|
图 4 推力杆二分之一模型 Fig. 4 Model of a half-thrust rod |
对杆体样品进行台架实验,在球铰压装实验中,单边过盈量为0.15mm,质量低于0.87kg的杆体,杆体末端都出现了裂缝,如图 5左所示,质量大于0.91kg以上的杆体没有出现裂缝;对压装合格的推力杆进行拉伸和压缩实验,实验样品数量各为5个,拉伸实验中杆体能承受的拉伸载荷集中在60~80kN,如图 5中所示,在压缩实验中,试样加载到-110kN出现了脆响,-150kN出现明显裂缝,如图 5右所示。

|
图 5 破坏位置 Fig. 5 Damage location |
采用传统的FEA分析方法,不考虑纤维取向对产品性能的影响,将长玻纤增强PA66(GF50)复合材料视为各向同性材料,选取表 2所示的弹性模量16.8GPa和泊松比0.33。橡胶球铰压入量为0.15mm,构件能承受一定的拉伸和压缩载荷,推力杆结构模型如图 6所示。单元类型为C3D8I,单元数为52824,节点数为66077。

|
图 6 推力杆结构模型 Fig. 6 Thrust rod structure model |
通过刚性面来模拟球铰压入工序,点A,B为刚性面的几何参考中心与杆体两孔中心重合,刚性面与杆体设置接触连接。分两步加载对杆体系统进行数值模拟,首先是对A,B两点进行固定约束,通过两刚性面与杆体进行挤压来模拟球铰压装;然后解除点B在Z轴方向的约束,通过设置分析步,在B点的Z方向施加集中力F,F值的正和负,分别表示杆件拉、压。模拟推力杆拉伸或压缩,有限元分析结果显示,三种状况下显示的最大主应力分别为96.2,107,132MPa,与实验结果对比如图 7所示。从图 7可知,传统FEA各向同性仿真分析得到的球铰压装和推力杆拉伸危险点位置与实验结果吻合度不高。

|
图 7 危险点与破坏位置 (a)球铰压装0.15mm;(b)拉伸69kN;(c)压缩120kN Fig. 7 Danger point and damage location (a)spherical hinge pressure 0.15mm; (b)stretch 69 kN; (c)compression 120 kN |
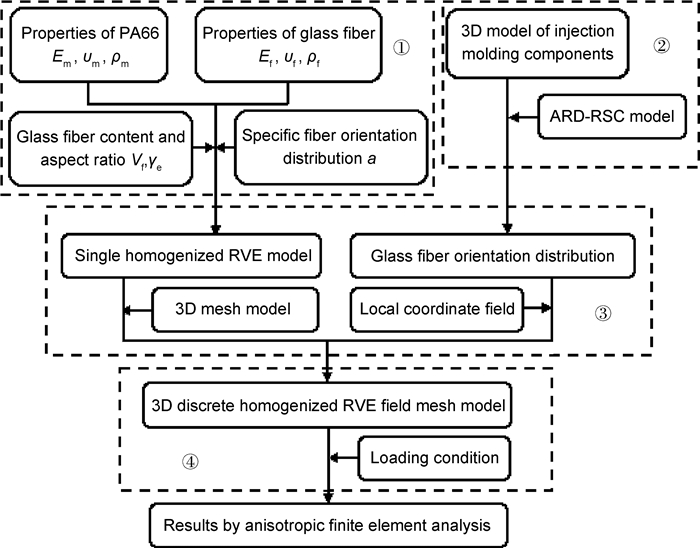
为了能够准确分析预测玻纤增强复合材料注塑结构件的承载能力和破坏位置,采样各向异性方法进行强度分析的核心是建立玻纤增强复合材料注塑结构件各向异性有限元离散模型。基于细观力学原理,综合运用复合材料细观建模、注塑成型和结构有限元分析技术,本工作提出了长玻纤增强复合材料注塑构件各向异性分析方法,分析流程如图 8所示。
|
图 8 长玻纤增强复合材料注塑构件各向异性分析流程 Fig. 8 Anisotropic analysis workflow of long glass fiber reinforced composite injection molding engineering structure |
各向异性分析方法工作流程主要由4部分组成。具体如下:
① 基于复合材料细观力学的Eshelby夹杂理论,应用Mean Field均匀化方法,建立玻纤增强复合材料纤维均质化RVE模型,并求出其正交各向异性弹性常数;
② 基于广义牛顿流体本构方程,采用ARD-RSC纤维取向模型,考虑纤维间相互作用,应用数值模拟纤维增强复合材料注塑加工过程,预测注塑结构件的纤维取向分布;
③ 对于注塑构件整体而言,由于不同位置点的纤维取向不尽相同,导致材料各向异性弹性常数随位置坐标的变化而变化。本工作将推力杆构件划分的每一个有限单元看作是一个RVE模型,构建离散的RVE模型场,对每一个RVE模型沿纤维取向建立局部坐标系,通过局部坐标系和全局整体坐标之间的转化关系,可获构件在整体坐标系下的材料各向异性弹性常数分布,进而建立构件有限元3D离散均质化RVE场网格模型。为了保证产品质量,塑件的壁厚应尽量控制在10mm以下,壁厚方向的节点设置相对较密。在建立有限单元局部坐标系时,六面体网格的厚度方向为2方向,距离最小,熔体流动方向为3方向,垂直于厚度方向和熔体流动方向为1方向,具体局部坐标系如图 9所示;
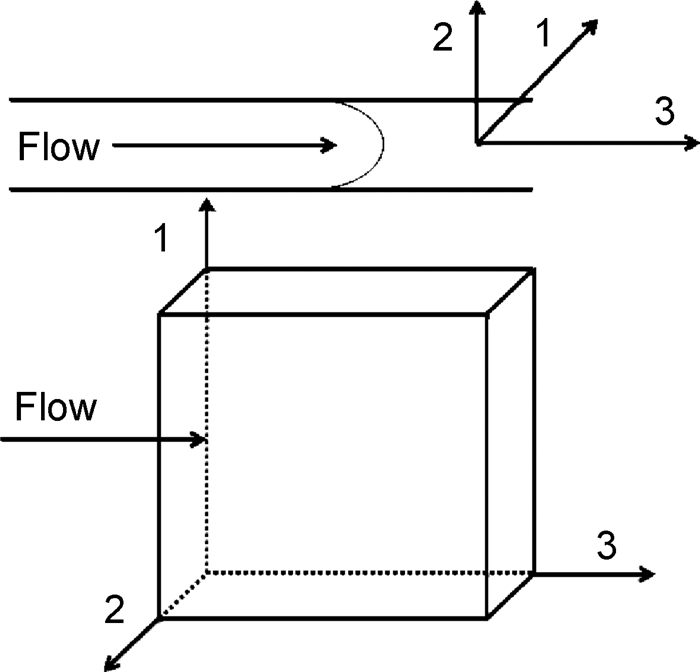
|
图 9 局部坐标系设计 Fig. 9 Local coordinate system design |
④ 基于结构有限元分析技术,设置加载和约束方式,对构件有限元3D离散均质化RVE网格模型进行应力应变分析,获取构件的各向异性强度分析结果。
2.4.2 塑件模流分析及纤维取向分布推力杆体采用长玻纤增强PA66(GF50)复合材料,玻纤初始长度为11mm,随着玻纤初始长度的增加纤维间的相互作用就会增加,从而加剧注塑成型过程中纤维的断裂。本工作基于广义牛顿流体本构方程,采用ARD-RSC纤维取向模型,建立成型工艺分析网格模型,设置实际工艺参数,数值模拟塑件注塑过程,预测注塑件的纤维取向分布,所得结果见图 10。
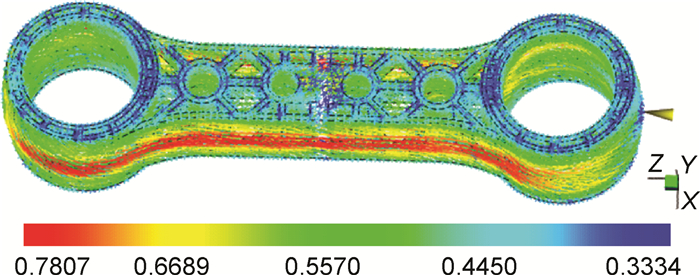
|
图 10 纤维取向分布 Fig. 10 Fiber orientation distribution |
数值模拟采用Moldflow材料库中的Verton RF-700-10-EM: SABIC Innovative Plastics US, LLC(50%长玻璃纤维增强型PA66),推荐的熔体温度范围280~300℃。对推力杆实体模型先用Moldflow软件对其划分双面层网格,接着对双面层网格进行修复,然后将其转为3D网格,网格尺寸为6mm,单元数为571667。工艺路线:注塑-保压-冷却,模具温度90℃,熔体温度为290℃,注塑时间为6s,保压时间130s,保压压力110MPa,冷却时间40s。图 10中的数值表示纤维取向张量主因子λ3,即纤维在熔体流动方向的集度,数值越趋近于1,纤维取向方向越趋于一致,也越能体现纤维在这一方向的承载能力。
2.4.3 材料细观模型与FEA分析基于复合材料细观力学的Eshelby夹杂理论,应用Mean Field均匀化方法,建立长玻纤增强PA66(GF50)复合材料均质化RVE模型。注塑成型后纤维长度主要分布在2~4mm,粒子直径为15μm,设置纤维长径比为220,纤维含量为50%(质量分数)。
对塑件进行有限元结构分析的加载方式与2.3节相同。由表 1可知,玻纤强度远高于PA66基体的强度,因此玻纤增强复合材料注塑结构件沿着纤维分布方向的增强效果最明显,承载能力也最强。根据这一特性,根据注塑成型过程中形成的纤维取向分布,推力杆的杆头部分纤维呈现同心圆取向分布,应用柱坐标下显示的应力来判断其是否破坏,杆体中间部分近似看成长方体,应用直角坐标下显示的应力结果来判断其是否破坏。有限元结构分析结果与实验结果对比见图 11所示。
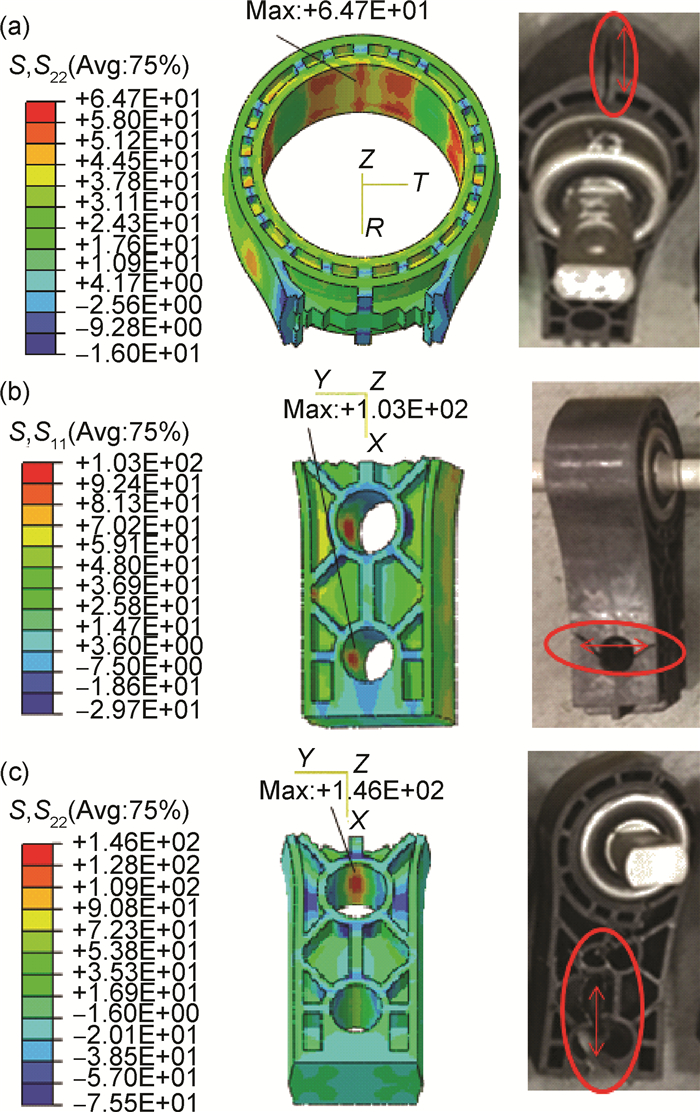
|
图 11 危险点与破坏位置 (a)球铰压装0.15mm;(b)拉伸69kN;(c)压缩120kN Fig. 11 Danger point and damage location (a)spherical hinge pressure 0.15mm; (b)stretch 69kN; (c)compression 120kN |
最大主应力分别为64.7, 103, 146MPa。考虑到浇注口纤维分布较为混乱降低了该处的结构强度,以及熔接缝的强度较低,对比杆体台架实验破坏位置图,显示仿真危险位置与实际破坏位置较为吻合,证明了各向异性分析方法的精准性与可行性。在推力杆压缩实验中,试样加载到-110kN出现了脆响,-150kN出现明显裂缝,说明在-110kN时,推力杆基体局部已发生破坏。在压缩载荷为120kN时,各向异性分析与各向同性仿真分析应力结果分别为146,132MPa,表明在同样载荷下,能表征纤维增强效果的各向异性分析能提前发现危险点,相对差值为10.6%。
2.5 推力杆结构改进由于杆体中部圆孔对杆体强度影响很大,同时考虑加强浇注口处与熔接缝强度,对推力杆结构进行改进设计,新的杆体结构如图 12所示。单元类型为C3D8I,单元数为32192,节点数为43305。参照2.4节各向异性分析方法,纤维取向分布如图 13所示,单元类型为3D,网格尺寸为6mm,单元数为700533。有限元分析结果见图 14。

|
图 12 推力杆新结构模型 Fig. 12 New structure model of thrust rod |
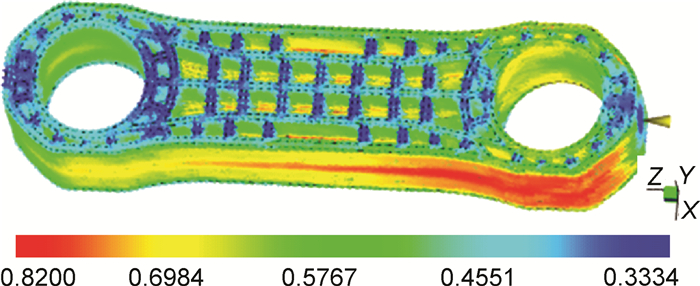
|
图 13 纤维取向分布 Fig. 13 Fiber orientation distribution |
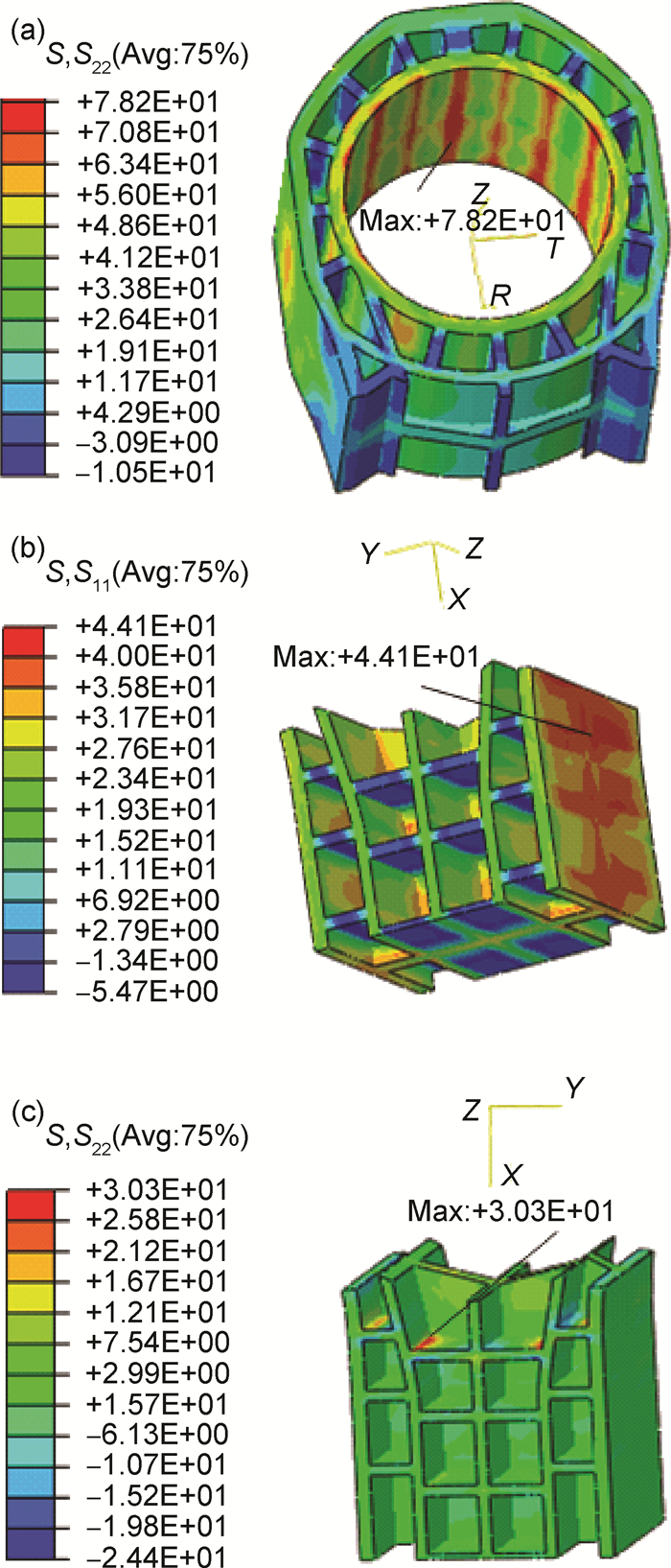
|
图 14 危险点主应力 (a)球铰压装0.15mm;(b)拉伸69kN;(c)压缩120kN Fig. 14 Dangerous point principal stress (a)spherical hinge pressure 0.15mm; (b)stretch 69kN; (c)compression 120kN |
对推力杆结构进行改进后,杆体中间部分强度有了显著提升,结构改进前后性能比对如表 3所示。
| Load | Principal stress/MPa | Optimizationeffect/% | |
| Original | New | ||
| 1 | 64.7 | 78.2 | +20.87 |
| 2 | 103.0 | 44.1 | -57.18 |
| 3 | 146.0 | 30.3 | -79.25 |
(1) 基于广义牛顿流体本构方程,采用ARD-RSC纤维取向模型,考虑纤维间相互作用,仿真预测长玻纤增强复合材料注塑构件的纤维取向分布;应用复合材料细观力学Eshelby夹杂理论和Mean Field均匀化方法,建立长玻纤增强复合材料均质化RVE模型。
(2) 综合运用复合材料细观建模、离散RVE模型场、注塑成型和结构有限元分析技术,提出了长玻纤增强复合材料注塑构件各向异性强度分析方法。
(3) 对推力杆注塑构件进行各向异性强度分析,显示仿真危险位置与实际破坏位置较为吻合。在此基础上对推力杆进行结构改进,结果表明杆体中间部分在拉伸载荷下的最大主应力降低了57.18%,在压缩载荷下的最大主应力降低了79.25%。
| [1] |
马鸣图, 易红亮, 路洪洲, 等. 论汽车轻量化[J].
中国工程科学, 2009, 11 (9): 20–27.
MA M T, YI H L, LU H Z, et al. On the light-weighting of automobile[J]. Engineering Sciences, 2009, 11 (9): 20–27. |
| [2] |
冯美斌. 汽车轻量化技术中新材料的发展及应用[J].
汽车工程, 2006, 28 (3): 213–220.
FENG M B. Development and applications of new materials in automotive light-weighting technologies[J]. Automotive Engineering, 2006, 28 (3): 213–220. |
| [3] |
熊爱华, 柳和生, 黄益宾, 等. 长玻纤增强聚合物注塑充填行为和纤维取向模拟[J].
高分子材料科学与工程, 2015, 31 (10): 110–114.
XIONG A H, LIU H S, HUANG Y B, et al. 3D simulation of filling behavior and fiber orientation for long glass fiber reinforced polymer composites during injection molding process[J]. Polymeric Materials Science and Engineering, 2015, 31 (10): 110–114. |
| [4] | CHUN H H. Young's modulus of unidirectional discontinuous-fibre composites[J]. Composites Science & Technology, 2000, 60 (14): 2671–2680. |
| [5] | MONDALI M, ABEDIAN A, GHAVAMI A. A new analytical shear-lag based model for prediction of the steady state creep deformations of some short fiber composites[J]. Materials & Design, 2009, 30 (4): 1075–1084. |
| [6] | SHARMA M, RAO I M, BIJWE J. Influence of fiber orientation on abrasive wear of unidirectionally reinforced carbon fiber-polyetherimide composites[J]. Tribology International, 2010, 43 (5/6): 959–964. |
| [7] |
任超, 陈建钧, 潘红良. 随机短纤维增强复合材料弹性模量预测模型[J].
复合材料学报, 2012, 29 (4): 191–194.
REN C, CHEN J J, PAN H L. Prediction model for elastic modulus of random short fiber reinforced composite[J]. Acta Materiac Compositae Sinica, 2012, 29 (4): 191–194. |
| [8] | ESHELBY J D. The determination of the elastic filed of ellipsoidal inclusion and related problems[J]. Proceedings of the Royal Society London Series A, 1957, 241 (1226): 367–396. |
| [9] | HILL R. A self-consistent mechanics of composite materials[J]. Journal of the Mechanics & Physics of Solids, 1965, 13 (4): 213–222. |
| [10] | MORI T, TANAKA K. Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metallurgica, 1973, 21 (5): 571–574. DOI: 10.1016/0001-6160(73)90064-3 |
| [11] | BRETHERTON F P. The motion of rigid particles in a shear flow at low reynolds number[J]. Journal of Fluid Mechanics, 1962, 14 (2): 284–304. DOI: 10.1017/S002211206200124X |
| [12] | FOLGAR F, TUCKER C L. Orientation behavior of fibers in concentrated suspensions[J]. Journal of Reinforced Plastics & Composites, 1984, 3 (2): 98–119. |
| [13] | WANG J, OGARA J F, TUCKER C L. An objective model for slow orientation kinetics in concentrated fiber suspensions:theory and rheological evidence[J]. Journal of Rheology, 2008, 52 (5): 1179–1200. DOI: 10.1122/1.2946437 |
| [14] | PHELPS J H, TUCKER C L. An anisotropic rotary diffusion model for fiber orientation in short-and long-fiber thermoplastics[J]. Journal of Non-Newtonian Fluid Mechanics, 2009, 156 (3): 165–176. DOI: 10.1016/j.jnnfm.2008.08.002 |
| [15] |
沈观林, 胡更开, 刘彬.
复合材料力学[M]. 北京: 清华大学出版社, 2006: 41-52.
SHEN G L, HU G K, LIU B. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2006: 41-52. |
| [16] | BAY R S, TUCKER C L. Stereological measurement and error estimates for three-dimensional fiber orientation[J]. Polymer Engineering & Hyperlink Science, 1992, 32 (32): 240–253. |
| [17] | ADVANI S G, TUCKER C L. The use of tensors to describe and predict fiber orientation in short fiber composites[J]. Journal of Rheology, 1987, 31 (8): 751–784. DOI: 10.1122/1.549945 |
| [18] |
江青松, 柳和生, 熊爱华, 等. 长纤维增强聚合物注塑流动纤维取向分布数值模拟[J].
高分子材料科学与工程, 2015, 31 (3): 123–127.
JIANG Q S, LIU H S, XIONG A H, et al. Numerical simulation on the fiber orientation distribution during flow in injection molding of long fiber reinforced polymer[J]. Polymeric Materials Science and Engineering, 2015, 31 (3): 123–127. |
 2018, Vol. 46
2018, Vol. 46


