文章信息
- 陈亚军, 王先超, 王付胜, 周剑, 吴悦雷
- CHEN Ya-jun, WANG Xian-chao, WANG Fu-sheng, ZHOU Jian, WU Yue-lei
- 不同应力幅比加载下2A12铝合金的多轴疲劳性能
- Multiaxial Fatigue Properties of 2A12 Aluminum Alloy Under Different Stress Amplitude Ratio Loadings
- 材料工程, 2017, 45(9): 136-142
- Journal of Materials Engineering, 2017, 45(9): 136-142.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2016.000817
-
文章历史
- 收稿日期: 2016-07-06
- 修订日期: 2017-05-03
2A12铝合金具有良好的成型工艺和焊接性能,其比强度、断裂韧度较高且具有良好的耐腐蚀稳定性,在飞机结构中应用广泛,是构成机身蒙皮、翼梁、隔框等承力构件的重要材料[1, 2]。飞机在飞行过程中,其零部件往往受到多轴疲劳载荷的作用,相关的失效研究对飞机安全性能评估具有重要意义[3-7]。影响材料多轴疲劳寿命的因素很多,如加载应力幅比、相位差、等效应力等,而工程构件所承受的疲劳损伤多为不同因素的累积加载所致,因此,对疲劳损伤累积问题的研究是估算多轴疲劳寿命的关键[8-12]。目前,国内外研究往往集中在多轴单级加载以及单轴多级累积加载下材料的失效机理分析和寿命预测方面[13-18],Karolczuk等[13]对单级加载条件下基于临界面原理的多轴疲劳失效准则进行了回顾,Jiang等[14]通过单级加载实验对3种多轴疲劳失效准则的预测效果进行了研究,Zuo等[17]考虑加载历史的影响,建立了一种新的非线性损伤累积模型,并对单轴多级变幅加载条件下的实验结果进行验证,冯胜等[18]考虑单轴多级累积条件下加载顺序和领域潜在损伤对材料疲劳寿命的影响,建立了一种新的疲劳破坏准则。但对于应力幅比、相位角等关键因素影响多级加载下的多轴疲劳损伤累积和失效行为的报道较少。本工作考虑某型单旋翼直升机尾旋翼实心变距拉杆的实际尺寸和受力情况,采用2A12航空铝合金实心棒材试样进行实验研究,分别进行单级、两级应力幅比条件下的多轴疲劳实验,通过分析加载过程中的循环曲线,并结合使用Hitachi S-3400N扫描电子显微镜对疲劳断口进行观察,来探究多轴疲劳失效断裂的影响规律。
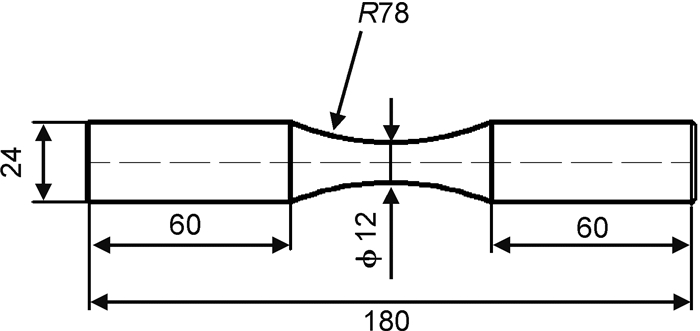
1 实验材料与方法实验材料选用2A12铝合金, 主要化学成分(质量分数/%)分别为:Cu 3.8~4.9, Mg 1.2~1.8, Mn 0.2~0.9, 其他为铝和部分杂质。常温下该材料的屈服强度为373.7MPa,抗拉强度为526.8MPa,弹性模量为78.5GPa。采用实心圆柱形试样进行多轴疲劳实验,具体尺寸如图 1所示。
|
图 1 疲劳试件尺寸图 Fig. 1 Schematic illustration of the fatigue specimen |
实验所用仪器为SDN100/1000电液伺服拉扭复合疲劳试验机,实验在常温下进行。采用正弦波对称加载,加载频率f=5Hz,疲劳破坏定义为试样的完全断裂。采用Von Mises等效应力准则,等效应力设定为350MPa,应力幅比λ定义为拉压应力幅与扭转应力幅之比,相关表达式如下:
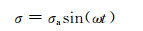
|
(1) |
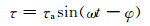
|
(2) |
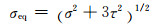
|
(3) |
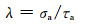
|
(4) |
式中:σa,τa分别为拉压应力幅值与扭转应力幅值;ω为实验角频率;φ为加载相位差,实验中均设定为0°。
为系统研究不同应力幅比加载条件下2A12铝合金的多轴疲劳失效规律,首先进行应力幅比为0,0.5,1,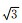
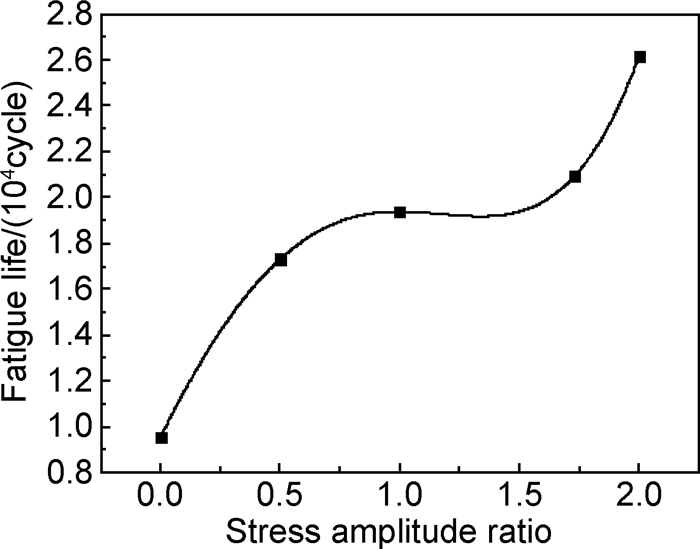
等效应力加载条件下,纯扭转加载时疲劳寿命最低为9539周,应力幅比为0.5时,疲劳寿命为17307周,应力幅比增加到2时,多轴疲劳寿命提高到26150周。图 2为不同应力幅比加载条件下2A12铝合金的多轴疲劳寿命曲线,可以看出,随应力幅比的增加,材料的多轴疲劳寿命得以提高。当前实验条件下,在承受多轴加载直至断裂的过程中,材料的疲劳寿命大部分消耗在裂纹萌生阶段,而切应力的扭转作用对裂纹萌生具有重要影响。应力幅比增大,拉压作用增强,同时扭转作用减弱,切应力的破坏作用减小,延缓了试样疲劳裂纹的产生,从而引起材料多轴疲劳寿命的增加。
|
图 2 2A12铝合金多轴疲劳寿命与应力幅比关系曲线 Fig. 2 Relation curve between multiaxial fatigue life and stress amplitude ratio of 2A12 aluminum alloy |
图 3为不同应力幅比下试样的宏观断口形貌,纯扭转加载作用下断口呈现出与试样主轴近似垂直的平台区域,随应力幅比的持续增加,平台长度、断口与试样主轴间的夹角逐渐减小,应力幅比为2时断面与试样主轴大致成45°的夹角。

|
图 3 不同应力幅比下试样断裂外观形貌
(a)λ=0;(b)λ=0.5;(c)λ=1;(d)λ=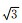 ;(e)λ=2 Fig. 3 Morphologies of fatigue fracture of specimens under different stress amplitude ratios
(a)λ=0;(b)λ=0.5;(c)λ=1;(d)λ= ;(e)λ=2 Fig. 3 Morphologies of fatigue fracture of specimens under different stress amplitude ratios
(a)λ=0;(b)λ=0.5;(c)λ=1;(d)λ=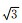 ;(e)λ=2 ;(e)λ=2 |
不同应力幅比下疲劳断口的形貌差别较大,但都可以明显分为裂纹源区、扩展区、瞬断区3部分。图 4为5种应力幅比下裂纹扩展区的微观形貌,从图 4(a)可以看出,纯扭转(λ=0) 加载条件下,断口裂纹扩展区表面较为平整,存在部分光滑的区域,这是由于主裂纹萌生和扩展过程中,其两侧受到较强的旋转摩擦作用,凸起的脊棱在循环过程中磨损消失。由图 4(b)中可以观察到大量的划痕以及表面部分脱落的颗粒,扭转作用的相对减弱使得平滑区域转化为大量近似平行的层状划痕,断口形貌变得更加破碎。图 4(c)中存在模糊的疲劳条带,右侧沿疲劳条带扩展方向有鳞片状凸起,这是循环过程中凸起脊棱的摩擦所致。随着拉压应力的增强以及扭转作用的降低,图 4(d)中疲劳条带变得清晰,在断面可以观察到鱼骨状形貌和近似垂直于主扩展方向的二次裂纹,伴随着主裂纹的扩展,试样内部应力集中部位会萌生二次微裂纹,当扩展的主裂纹穿过该区域时,微裂纹便停止扩展而留存下来。如图 4(e)所示, 应力幅比为2时断口可以观察到大量鳞片状、鱼骨状形貌。

|
图 4 不同应力幅比下裂纹扩展区微观形貌
(a)λ=0;(b)λ=0.5;(c)λ=1;(d)λ=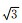 ;(e)λ=2 Fig. 4 Micro morphologies in crack propagation region under different stress amplitude ratios
(a)λ=0;(b)λ=0.5;(c)λ=1;(d)λ= ;(e)λ=2 Fig. 4 Micro morphologies in crack propagation region under different stress amplitude ratios
(a)λ=0;(b)λ=0.5;(c)λ=1;(d)λ=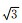 ;(e)λ=2 ;(e)λ=2 |
应力幅比为1时,在断口瞬断区可观察到如图 5所示的特殊形貌。拉压应力作用下产生的大量韧窝堆叠在一起形成了蜂窝状形貌,附近可以看到一些孔洞和剪切型韧窝,这是由于切应力的旋转摩擦作用所造成的。大量韧窝的存在说明在此应力幅比条件下,拉压方向应力在瞬间断裂阶段起着重要作用。

|
图 5 应力幅比为1时瞬断区蜂窝状形貌 Fig. 5 Honeycomb feature in the transient fracture zone at λ=1 |
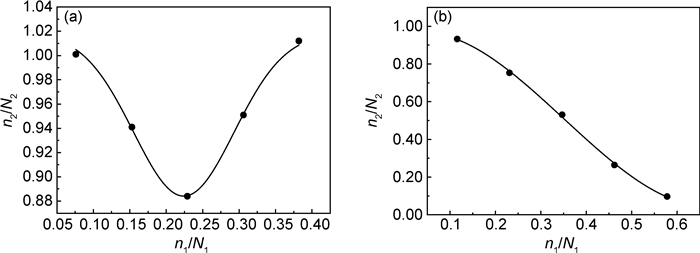
表 1记录了两类应力幅比累积条件下的测试结果,其中n1,n2分别为一级,二级加载周次;N1,N2分别为一级,二级应力幅比单级加载条件下的多轴疲劳总寿命;n1/N1,n2/N2分别定义为一,二两级加载条件下的损伤比,根据Miner线性叠加原理,(n1/N1)+(n2/N2)为两级加载条件下的总损伤比。由表 1可以看出, 2→0.5加载路径下,总损伤比的值均大于1,且随一级加载周次的增加,总损伤比逐渐增大。0.5→2加载路径下总损伤比的值多数小于1,且随一级加载周次的增加,总损伤比呈递减趋势。图 6为两类加载路径下二级损伤比随一级损伤比的变化曲线,如图 6(a)所示,2→0.5加载路径下随一级损伤比的增加,二级损伤比先降低后逐渐升高,体现出“锻炼效应”的特征;图 6(b)为0.5→2加载时的关系曲线,由于一级低应力幅比加载时切应力较强的破坏作用,造成二级损伤比随一级损伤比的增加快速降低。
| Cumulative path | n1/cycle | Fatigue life/cycle | n1/N1 | n2/N2 | (n1/N1)+(n2/N2) |
| 2→0.5 | 2000 | 19320 | 0.076 | 1.001 | 1.077 |
| 4000 | 20285 | 0.153 | 0.941 | 1.094 | |
| 6000 | 21291 | 0.229 | 0.884 | 1.113 | |
| 8000 | 24458 | 0.306 | 0.951 | 1.257 | |
| 10000 | 27516 | 0.382 | 1.012 | 1.394 | |
| 0.5→2 | 2000 | 26360 | 0.116 | 0.932 | 1.048 |
| 4000 | 23609 | 0.231 | 0.750 | 0.981 | |
| 6000 | 19890 | 0.347 | 0.531 | 0.878 | |
| 8000 | 14428 | 0.462 | 0.246 | 0.708 | |
| 10000 | 12525 | 0.578 | 0.097 | 0.675 |
|
图 6 二级损伤比与一级损伤比关系曲线 (a)2→0.5;(b)0.5→2 Fig. 6 Relation curves between the second stage damage ratio and the first stage damage ratio (a)2→0.5;(b)0.5→2 |
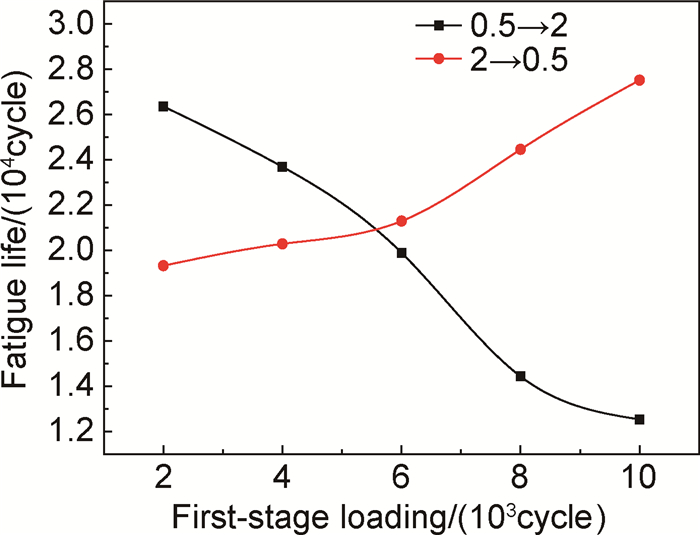
两类累积实验条件下,多轴疲劳寿命随一级加载周次的变化如图 7所示。2→0.5加载路径下,随一级(λ=2) 循环周次的增加,材料的疲劳寿命持续增大,较大的应力幅比对应着较小的扭转力矩,对材料的破坏作用较弱,应力幅比为2→0.5,扭转作用的破坏能力增强,材料受到的破坏作用增大,随一级加载周次的增加,高→低应力幅比作用顺序下产生的“锻炼效应”使多轴疲劳寿命得以提高;0.5→2加载路径下,随一级(λ=0.5) 循环周次的递增,多轴疲劳寿命逐渐减小。应力幅比为0.5时,材料受到的破坏作用较强,且随着一级加载周次的增多,受损程度变得更加严重,引起总体疲劳寿命的降低。
|
图 7 疲劳寿命与一级加载周次关系曲线 Fig. 7 Relation curves between the total fatigue life and the cycle of the first stage loading |
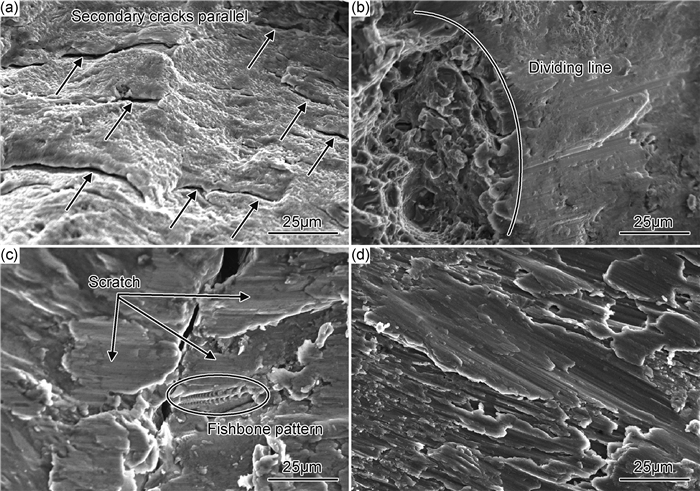
图 8(a)~(d)分别为两类加载方式下一级循环2000周次和10000周次的断口微观形貌。从图 8(a)中可以观察到大量平行分布的二次裂纹,材料在拉扭复合加载条件下,内部不均匀处更容易产生应力集中,当集中的应力超过不均匀体与均匀体之间的结合力时,就会萌发微裂纹。图 8(b)为典型的多轴疲劳微观形貌,以弧线为界可明显分为两个区域,弧线右侧较为光滑,可以看到较强切应力作用下所产生的明显划痕,弧线左侧呈现出拉压作用下的断面形貌。图 8(c)中裂纹两侧均可观察到大量划痕,其中裂纹右侧发现鱼骨状形貌,由于低应力幅比加载周次相对较少,这一形貌未被磨损得以保存下来。由于应力幅比为2时的加载周次较短,材料大部分寿命消耗在较强的扭转作用条件下,在图 8(d)中可以观察到大量明显的划痕。
|
图 8 两类累积方式断口微观形貌 (a)2→0.5, 一级加载2000周次; (b)2→0.5, 一级加载10000周次; (c)0.5→2, 一级加载2000周次; (d)0.5→2, 一级加载10000周次 Fig. 8 Micro morphologies of the two cumulation loading paths (a)2→0.5, first stage loading 2000 cycles; (b)2→0.5, first stage loading 10000 cycles; (c)0.5→2, first stage loading 2000 cycles; (d)0.5→2, first stage loading 10000 cycles |
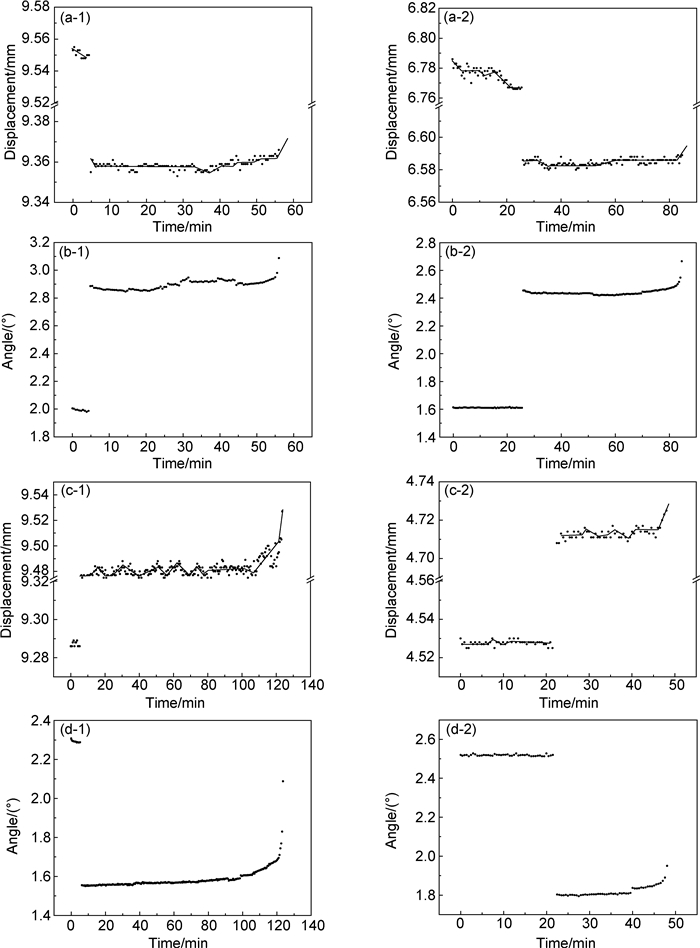
实验加载稳定后,每隔30s记录1次位移、扭角峰值,选取两类累积方式下一级循环周次分别为2000与10000时记录的数据,绘制出相应加载方式下位移、扭角峰值随时间的变化关系曲线,如图 9所示。图 9(a)为第一类加载方式下(2→0.5) 位移、扭角峰值随时间的变化关系,可知在沿轴方向一级高应力幅比加载时出现明显的循环硬化现象,转换到二级低应力幅比后,材料硬化现象不明显,经过一段时间的平台保持区后逐渐软化至断裂;扭转方向如图 9(b)所示,切换到二级加载方式后,开始阶段观察到了较小的循环硬化现象。应力幅比为2时轴向加载所产生的硬化现象使材料得到“锻炼”,且随着高应力幅比作用周次的增加,低应力幅比下较强切应力的作用周次缩短,进而延长了试样的多轴疲劳寿命。图 9(c)为第二类加载方式下(0.5→2) 位移、扭角幅值随时间的变化关系曲线,当切换到二级高应力幅比加载阶段后,沿轴方向可以看到循环硬化、软化交替出现的现象,扭转方向如图 9(d)所示,开始阶段扭角随时间基本保持不变后逐渐软化至试样断裂,随着一级低应力幅比加载周次的增加,较强切应力的作用时间变长,加速了材料的疲劳断裂。
|
图 9 不同累积方式下位移及扭角幅值随时间变化曲线 1-一级循环2000周次;2-一级循环10000周次 (a)2→0.5拉压方向; (b)2→0.5扭转方向; (c)0.5→2拉压方向; (d)0.5→2扭转方向 Fig. 9 Displacement-time curves and torsional angle-time curves under different cumulative paths 1-first stage loading 2000 cycles; 2-first stage loading 10000 cycles (a)2→0.5, axial direction; (b)2→0.5, torsional direction; (c)0.5→2, axial direction; (d)0.5→2, torsional direction |
(1) 应力幅比从0增加到2,疲劳寿命周次从9539逐渐递增到26150。试样断面与主轴的夹角随应力幅比的增加逐渐减小,应力幅比为0时断面存在平整的光滑区域,随应力幅比的增加断面划痕减少,能观察到疲劳条带以及鱼骨状、鳞片状和蜂窝状特殊形貌。
(2)2→0.5累积条件下,随一级加载周次增加,出现“锻炼效应”特征,试样疲劳寿命提高;0.5→2累积条件下,随一级低应力幅比加载周次增加,试样疲劳寿命逐渐降低。两类加载方式下试样断口可见大量平行的二次裂纹、切应力引起的划痕以及鱼骨状特殊形貌。
(3)2→0.5累积条件下,拉压方向一级高应力幅比加载时出现明显的循环硬化现象,转换到二级低应力幅比后,材料硬化现象不明显;0.5→2加载时,二级高应力幅比加载阶段,拉压方向循环硬化、软化交替出现,扭转方向在开始阶段扭角随时间基本保持不变,后逐渐软化直至试样断裂。
| [1] |
中国航空材料手册编辑委员会.
中国航空材料手册:第3卷 铝合金 镁合金 钛合金[M]. 北京: 中国标准出版社, 1989.
Edit Committee of China Aeronautical Materials Handbook. China aeronautical materials handbook:volume Ⅲ aluminum alloy magnesium alloy titanium alloy[M]. Beijing: Standard Press of China, 1989. |
| [2] | STALEY J T, LIU J, HUNT Jr W H. Aluminum alloys for aerostructures[J]. Advanced Materials & Processes, 1997, 152 (4): 17–20. |
| [3] |
马楠楠, 陶春虎, 何玉怀, 等. 航空发动机叶片多轴疲劳试验研究进展[J].
航空材料学报, 2012, 32 (6): 44–49.
MA N N, TAO C H, HE Y H, et al. Research progress of multiaxial fatigue test methods on blades of aviation engine[J]. Journal of Aeronautical Materials, 2012, 32 (6): 44–49. |
| [4] |
童第华, 吴学仁, 刘建中, 等. 基于小裂纹理论的铸造钛合金ZTC4疲劳寿命预测[J].
材料工程, 2015, 43 (6): 60–65.
TONG D H, WU X R, LIU J Z, et al. Fatigue life prediction of cast titanium alloy ZTC4 based on the small crack theory[J]. Journal of Materials Engineering, 2015, 43 (6): 60–65. |
| [5] |
丁智平, 陈吉平, 王腾飞, 等. 镍基单晶合金多轴非比例加载低周疲劳研究[J].
力学学报, 2012, 44 (2): 326–333.
DING Z P, CHEN J P, WANG T F, et al. Study on low cycle fatigue of single crystal Ni-based superalloy under multiaxial non-proportional loading[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44 (2): 326–333. |
| [6] |
田玉杰, 尚德广, 陈宏, 等. 单多轴变幅加载下TC21钛合金疲劳特性[J].
航空材料学报, 2013, 33 (2): 74–80.
TIAN Y J, SHANG D G, CHEN H, et al. Fatigue properties of TC21 Ti-alloy under uniaxial and multiaxial cyclic variable amplitude loading[J]. Journal of Aeronautical Materials, 2013, 33 (2): 74–80. |
| [7] |
赵萍. 航空发动机单晶叶片的多轴低周疲劳研究[D]. 长沙: 中南大学, 2011. ZHAO P. Study on multi-axial low cycle fatigue of aero-engine single crystal blades[D]. Changsha:Central South University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10533-1011177803.htm |
| [8] |
夏天翔, 姚卫星, 许利蒲. LY12CZ铝合金在多轴两级阶梯谱下疲劳累积损伤理论的对比研究[J].
航空材料学报, 2014, 34 (3): 86–92.
XIA T X, YAO W X, XU L P. Comparative research on accumulative damage models under multiaxial 2-stage step loading spectra for LY12CZ aluminum alloy[J]. Journal of Aeronautical Materials, 2014, 34 (3): 86–92. |
| [9] |
张莉, 唐立强, 付德龙. 基于损伤累积理论的多轴疲劳寿命预测方法[J].
哈尔滨工业大学学报, 2009, 41 (4): 123–125.
ZHANG L, TANG L Q, FU D L. An evaluation method of fatigue life under multi-axial loading based on damage accumulation theory[J]. Journal of Harbin Institute of Technology, 2009, 41 (4): 123–125. |
| [10] | TAHERI S, VINCENT L, LE-ROUX J C. Classification of metallic alloys for fatigue damage accumulation:a conservative model under strain control for 304 stainless steels[J]. International Journal of Fatigue, 2015, 70 : 73–84. DOI: 10.1016/j.ijfatigue.2014.07.009 |
| [11] | MANSON S S, HALFORD G R. Practical implementation of the double linear damage rule and damage curve approach for treating cumulative fatigue damage[J]. International Journal of Fracture, 1981, 17 (4): 169–192. |
| [12] |
叶笃毅, 王德俊, 童小燕, 等. 一种基于材料韧性耗散分析的疲劳损伤定量新方法[J].
实验力学, 1999, 14 (1): 80–88.
YE D Y, WANG D J, TONG X Y, et al. A new approach for studying fatigue damage[J]. Journal of Experimental Mechanics, 1999, 14 (1): 80–88. |
| [13] | KAROLCZUK A, MACHA E. A review of critical plane orientationals in multiaxial fatigue failure criteria of metallic materials[J]. International Journal of Fracture, 2005, 134 (3/4): 267–304. |
| [14] | JIANG Y Y, HERTEL O, VORMWALD M. An experimental evaluation of three critical plane multiaxial fatigue criteria[J]. International Journal of Fatigue, 2007, 29 (8): 1490–1502. DOI: 10.1016/j.ijfatigue.2006.10.028 |
| [15] | SONSINO C M, LAGODA T, DEMOFONTI G. Damage accumulation under variable amplitude loading of welded medium-and high-strength steels[J]. International Journal of Fatigue, 2004, 26 (5): 487–495. DOI: 10.1016/j.ijfatigue.2003.10.001 |
| [16] | DJEBLI A, AID A, BENDOUBA M, et al. A non-linear energy model of fatigue damage accumulation and its verification for Al-2024 aluminum alloy[J]. International Journal of Non-Linear Mechanics, 2013, 51 : 145–151. DOI: 10.1016/j.ijnonlinmec.2013.01.007 |
| [17] | ZUO F J, HUANG H Z, ZHU S P, et al. Fatigue life prediction under variable amplitude loading using a non-linear damage accumulation model[J]. International Journal of Damage Mechanics, 2015, 24 (5): 767–784. DOI: 10.1177/1056789514553042 |
| [18] |
冯胜, 程燕平, 赵亚丽, 等. 线性疲劳损伤累积理论的研究[J].
哈尔滨工业大学学报, 2003, 35 (5): 608–610.
FENG S, CHENG Y P, ZHAO Y L, et al. Linear fatigue damage cumulation theory[J]. Journal of Harbin Institute of Technology, 2003, 35 (5): 608–610. |
 2017, Vol. 45
2017, Vol. 45


