文章信息
- 钟振前, 田志凌, 杨春
- ZHONG Zhen-qian, TIAN Zhi-ling, YANG Chun
- 马氏体不锈钢的微观组织各向异性对微区应力和氢分布的影响
- Microstructure Anisotropy Effect on Stress and Hydrogen Distribution in Micro Area for Martensitic Stainless Steel
- 材料工程, 2016, 44(10): 80-87
- Journal of Materials Engineering, 2016, 44(10): 80-87.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2016.10.012
-
文章历史
- 收稿日期: 2014-12-10
- 修订日期: 2015-12-28
2. 清华大学 材料学院, 北京 100083
2. School of Materials and Engineering, Tsinghua University, Beijing 100083, China
氢致延迟断裂是高强结构钢断裂失效的常见形式之一,应力、氢、材料三者的交互作用是氢致延迟断裂发生的主要原因。其中应力扮演了极其重要的角色,这是因为应力可以极大地提高氢在材料中的扩散能力,并使部分氢脱离氢陷阱的束缚[1],驱动氢向应力集中处扩散和聚集[2],最终萌生氢致延迟裂纹。
目前,应力对氢的扩散[3, 4]和聚集[5, 6]作用的研究更多集中在宏观尺度上,例如在加载应力条件下用电化学渗透方法研究氢的扩散行为,或通过预制缺口拉伸试样的方式计算缺口处的应力集中系数和氢的聚集浓度[7]。少量微观尺度上的氢扩散研究主要集中在氢与位错[8]或缺陷[9, 10]的相互作用,以及氢对局部[11, 12]塑性变形的影响等方面上,但对应力作用下氢在马氏体微观组织间的分布和富集的研究鲜有报道,而开展此项研究工作对探求氢脆微观机理和预防氢脆断裂事故的发生具有重要意义。
由于材料微观组织结构的各向异性,氢的微区分布是不均匀的,氢的局部浓度与多晶体材料中的微区应变相关,而微区应变由晶体弹性刚度[13, 14]的各向异性决定。本工作用弹性刚度计算微区应变的方法,与氢的Fick扩散定律结合起来,分析应力作用下氢在马氏体微观组织间的微区分布。该研究方法可概括为3个步骤:(1)通过电子背散射衍射(Electron Back Scatter Diffraction,EBSD)测定材料的微区弹性刚度[15, 16]分布;(2)利用软件Abaqus开发微观组织的数值模型计算微区应力;(3)根据应力对氢扩散的驱动作用,分析氢的局部聚集行为。
1 实验材料与方法 1.1 慢拉伸实验实验材料选用0Cr16Ni5Mo,其化学成分(质量分数/%)为:C 0.04,Si 0.39,Mn 0.78,P 0.027,S 0.012,Cr 15.81,Ni 5.25,Mo 1.05。经淬火(980℃×2h)+高温回火(500℃×4 h)调质热处理。
慢拉伸实验分别在快速渗氢溶液和大气中进行。制取两根板状拉伸试样(厚度2mm,宽度4mm,标距为30mm),表面粗糙度为Ra=3.2μm。将其中一根试样的中间部分浸入到快速渗氢液(0.5mol/L H2SO4 +少量 As2O3)中,两端夹持区固定在WDML-1型微机控制慢应变速率力学试验机上。在200mA/cm2的电流下预充氢4h后,以0.003mm/min的速率进行慢拉伸实验(充氢不停止)。另取一根同规格的试样在大气中以同样的加载速率进行慢拉伸实验。将拉断后的两试样置于SEM下(JSM-6400)观察并比较断口的微观形貌。
1.2 EBSD实验及微区弹性刚度分析制取纵截面金相试样,打磨、机械抛光和电解抛光(90%C2H5OH+10%HClO4,电压为23V)后,以0.5μm的步长进行EBSD实验。根据马氏体微观组织结构的晶体取向分布、滑移系和弹性刚度矩阵[17]计算横向(Transverse Direction,TD)的弹性刚度和Taylor因子,并将其大小和分布用颜色梯度在图中表示出来。Taylor因子计算时选用的滑移系是{110}〈111〉,这是bcc结构的多晶体材料在室温变形时最常见的滑移系。
2 有限元分析 2.1 力学模型根据微观组织(见图 1(a))形态和尺寸建立材料微区结构的有限元模型,模拟结构如图 1(b)所示,以1.5μm为单元尺寸进行网格划分,共得到4519个单元(如图 1(c)所示)。
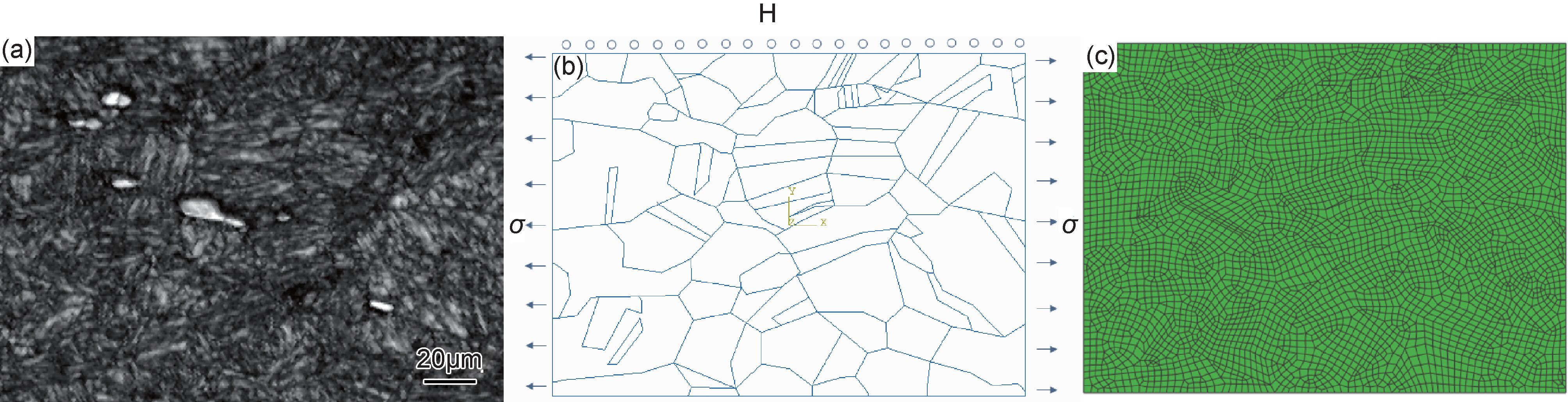
|
图 1 马氏体组织微区结构模型及边界条件 (a)板条马氏体微观组织结构;(b)在微观组织结构基础上建立模型;(c)网格划分 Fig. 1 Martensite microstructure model and boundary conditions (a) microstructure of lathmartensite;(b)numerical model based on microstructure;(c)mesh of model |
由于高强结构钢中位错运动对氢运输的贡献很小[18],因此忽略结构缺陷对氢的陷阱作用[7],假定氢的扩散富集只由应力驱动控制,应力对氢的扩散驱动遵循下列公式:
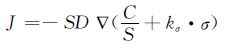
|
(1) |
式中:J表示扩散通量,g/(cm2·s);氢扩散率[19]D=6.7×10-13m2/s;σ为静应力,N/mm2;C为氢浓度,10-6;S为氢的溶解度,文献[20]建议S=1.89×10-10m·N$-\frac{1}{2}$;kσ是应力梯度系数,通过下式计算:
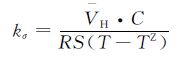
|
(2) |
氢在Fe中的偏摩尔体积VH=2.0×103mm3/mol,玻耳兹曼常数R=8.314J/(mol·K),TZ是绝对零度(-273℃)。
根据传质理论:
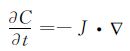
|
(3) |
将公式(1),(2)代入(3),得出应力与氢浓度的关系公式:
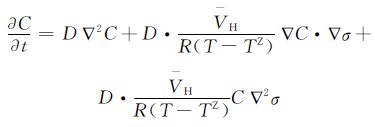
|
(4) |
力学计算完成后,将单位类型转换DCAX4,将应力代入公式(4)即可得出氢浓度。
2.3 材料参数及边界条件设定各节点的初始氢浓度C0设置为1×10-6,上边界氢浓度C设置为4×10-6,如图 1(b)所示。材料密度取7850kg/m3,泊松比取0.3。在模型的横向方向上加载均匀分布的应力,如图 1(b)中σ,并输入各板条束的弹性刚度,其值由EBSD实验得出,如图 2(a)所示。

|
图 2 马氏体组织的晶体取向、弹性刚度和Taylor因子 (a)弹性刚度分布图及3个Packet板条束的内部路径;(b)3个Packet内部路径的点对点取向差变化;(c)3个Packet内的弹性刚度分布曲线;(d)3个Packet内的Taylor factor的分布 Fig. 2 Crystal orientation,elastic stiffness and Taylor factor for martensite (a) the elastic stiffness distribution along 3 Paths respectively in the 3 Packets;(b) point to point misorientation distribution along 3 paths in the 3 Packets;(c)elastic stiffness distribution in the 3 Packets;(d)Taylor factor distribution in the 3 Packets |
图 2(a)是材料的弹性刚度分布图,可见Packet由许多平行的Block板条束组成,选取3个不同形状和尺寸的Packet板条束,如图 2(a)中Packet 1,Packet 2,Packet 3,在各Packet内部分别垂直于Block板条束作一条路径,如图中箭头所示路径,分析路径上不同组织单元的取向差、弹性刚度、Taylor因子的变化趋势。
图 2(b)中取向差分布曲线表明,3条不同路径上的取向差的变化规律较为一致,相邻Block板条束的取向差均为60°,同一Block板条束内的不同Lath板条取向差均基本在5°以内。
尽管3个路径上相邻Block板条束的取向差均为60°,但弹性模量和Taylor因子的大小没有明显的分布规律,如图 2(c),(d)所示,有些相邻板条束的弹性模量和Taylor因子相差很大(Packet 1,3内部的Block板条束),有些相差很小(Packet 2内部的Block板条束)。这是因为弹性刚度和Taylor因子是矢量,其大小主要与晶体取向和受力方向有关,而取向差是标量,其大小与受力方向无关,只由相邻板条束的取向关系决定。这在一定程度上表明,取向差只能表示晶界类型,并不能用来表征微区应变量。
Taylor因子可以用来表示多晶体材料中各晶体取向的胞元在某一受力方向上的变形能力,反映各胞元之间的形变约束关系和晶体滑移的优先性。弹性刚度和Taylor因子的变化曲线相近似,以及Taylor因子和弹性刚度之间的计算关系[21]表明,微区弹性刚度可以用来表征某一受力方向上的晶体滑移性能和微区应变。
3.2 弹性刚度和板条束的大小对氢浓度的影响将EBSD得到的弹性刚度实验数据输入模型中,进行应力和氢浓度的模拟计算。图 3(a)为没有外加应力时,氢从上边界向内扩散200s后的浓度分布图。氢浓度在X方向上呈均匀分布,在Y方向上呈梯度分布,以边界浓度最高,向内依次逐渐降低;因此,无应力作用时,氢的浓度变化只与浓度梯度和扩散时间有关,而与板条束的弹性刚度无关。图 3(b)为外加均布载荷80MPa下的应力云图,如σL为各Block板条束上的局部应力,σ0为边界均布应力,定义应力集中系数α=σL/σ0,根据应力云图可以计算各Block板条束的应力集中系数。图 3(c)为同样加载条件下氢浓度的分布图。对照图 3(b),(c)可见,氢的浓度分布与应力分布规律基本一致,应力集中系数高的区域其氢浓度也较高。
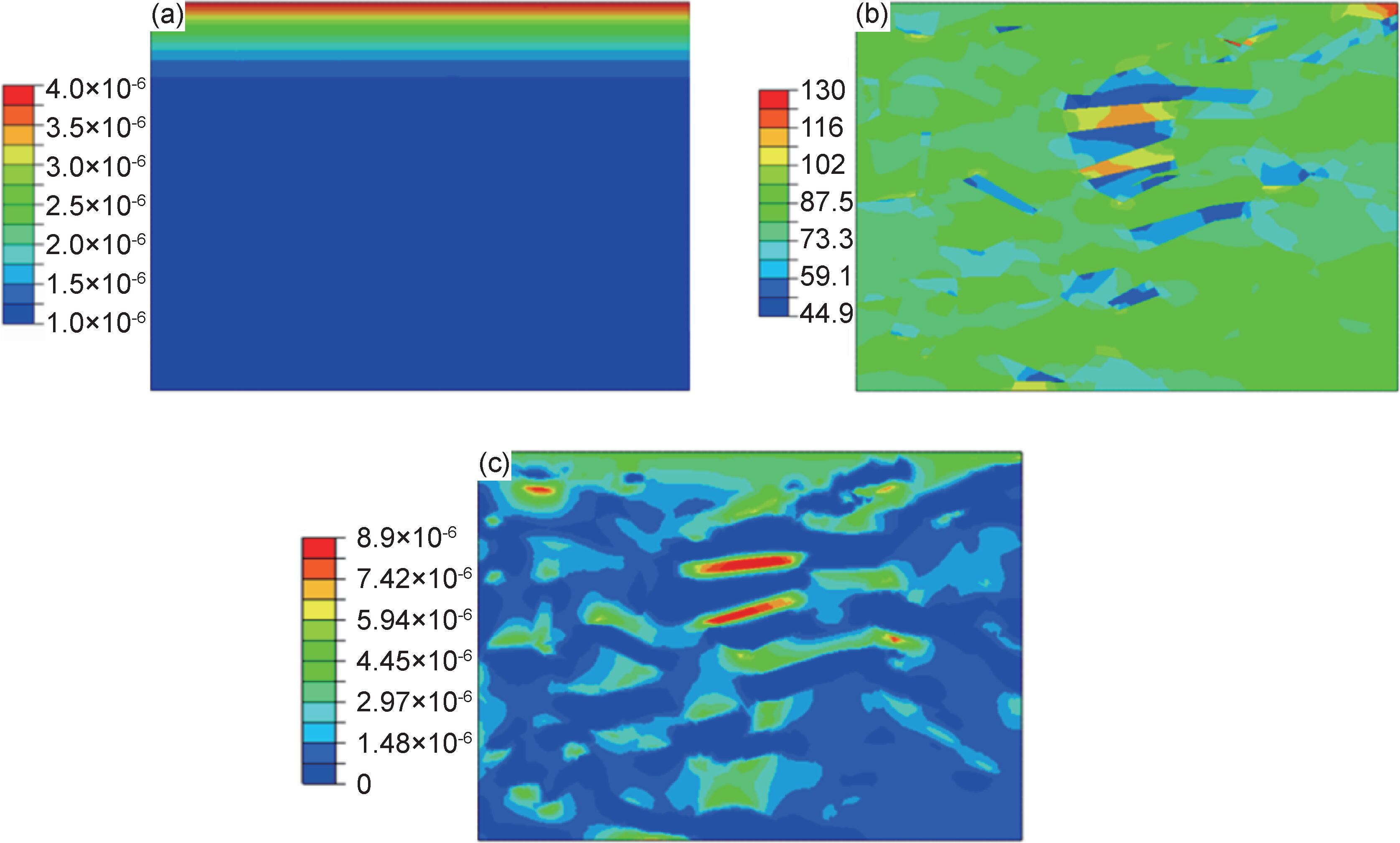
|
图 3 应力及氢浓度分布 (a) 无应力作用时氢的浓度分布;(b)加载80MPa时应力在组织间的分布;(c)加载80MPa时氢浓度的分布 Fig. 3 Distribution of stress and hydrogen concentration (a) hydrogen diffusion by hydrogen concentration gradient with no stress driving;(b) stress distribution under uniformed load of 80MPa on the boundary;(c) hydrogen concentration distribution under uniformed load of 80MPa |
在应力云图和氢分布图的不同Block板条束上采集计算数据,分析弹性刚度梯度(相邻Block的弹性刚度之差)和板条束长度尺寸对氢浓度和应力集中系数的影响,如图 4(a),(b)所示,可见随着这些参数的增大,应力集中系数和氢浓度总体也在增加。
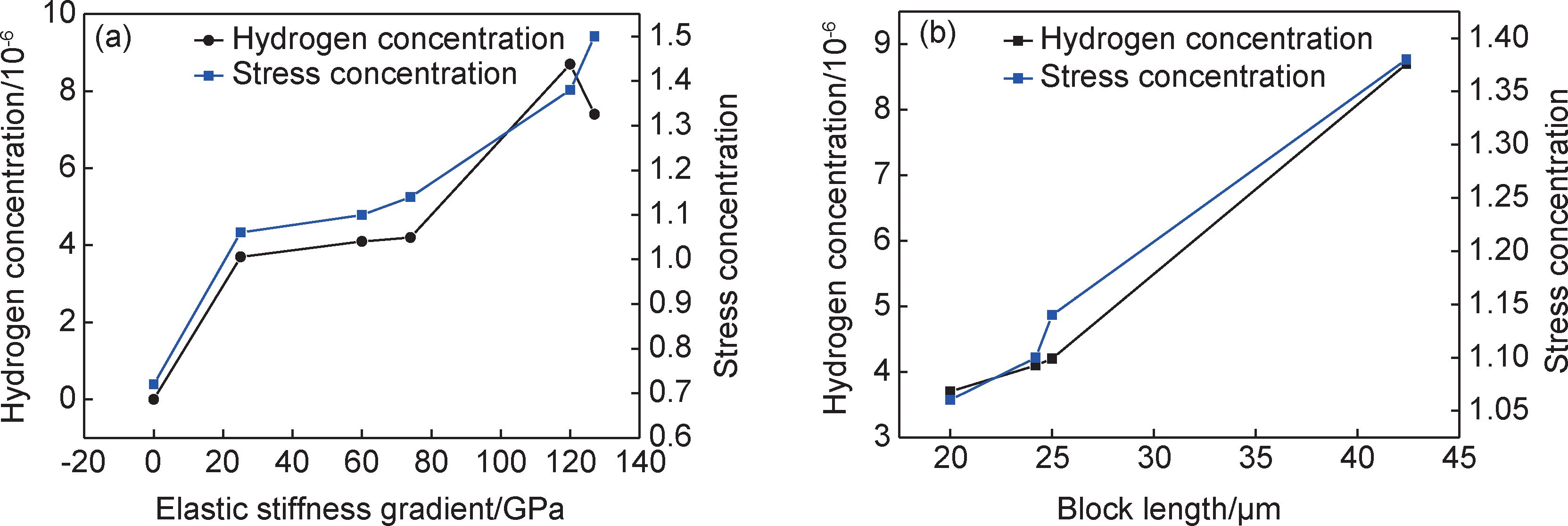
|
图 4 弹性刚度梯度(a)和Block尺寸(b)对应力集中系数和氢浓度的影响 Fig. 4 Effects of elastic stiffness gradient (a) and Block length (b) on the stress concentration and hydrogen concentration |
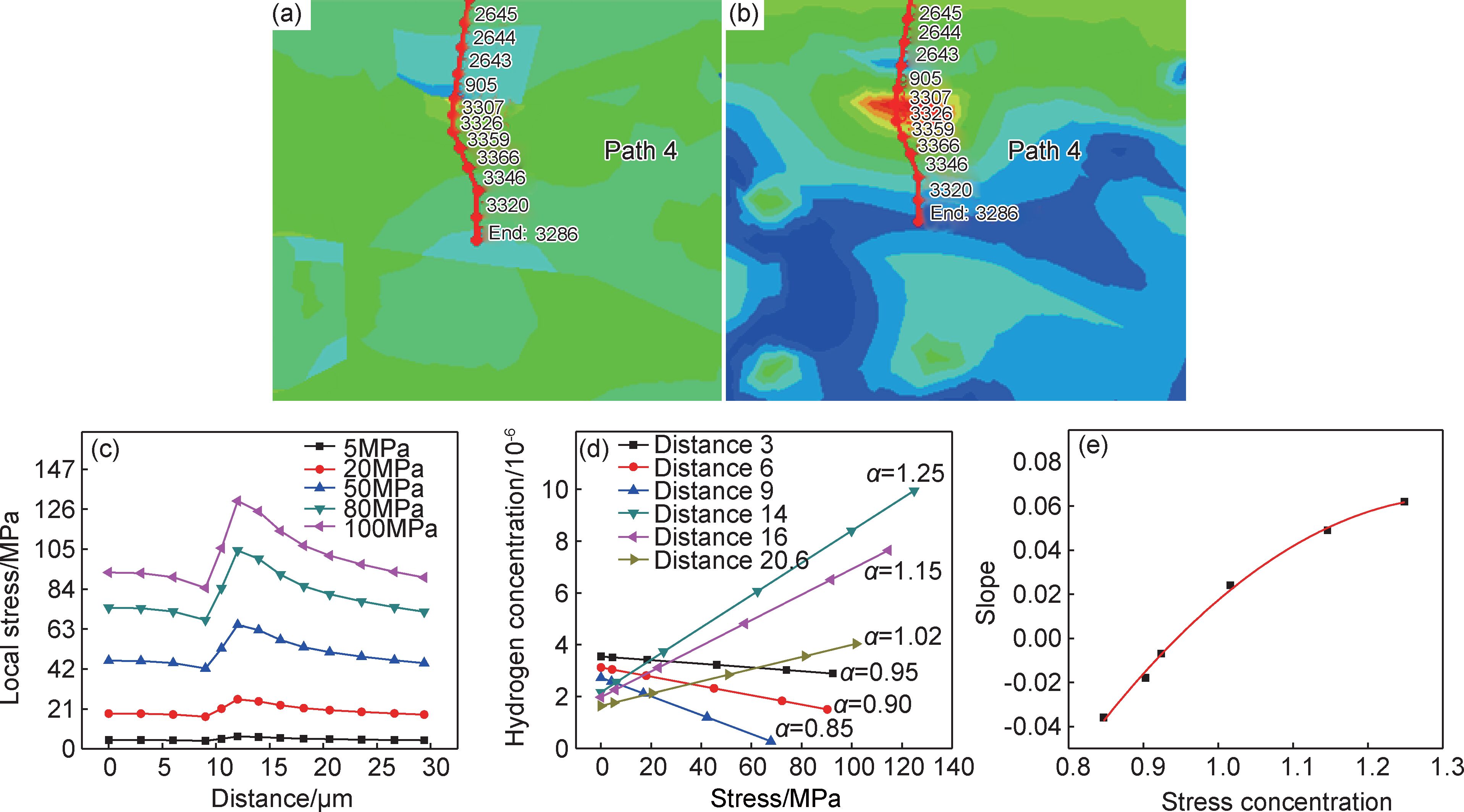
图 5(a)为从应力云图上截取的部分区域,该区域对应的氢浓度分布如图 5(b)所示;在两张放大图上设定分析路径。在边界应力σ0分别为5,20,50,80,100MPa时,分析路径上各位置的应力和氢浓度。图 5(c)可见增大边界应力σ0时,各位置的局部应力σL也随之线性增大。图 5(d)中分析了距离上边界分别为3,6,9,14,16,20.6μm等位置(在图中用Distance 3,Distance 6……表示)的氢浓度,可见各位置的氢浓度随应力的增大线性增加或减少,其中应力集中系数α>1位置的氢浓度随应力的增大而线性增加,斜率k为正;而α<1位置的氢浓度随应力的增大反而线性减少,斜率k为负。图 5(e)对图 5(d)中各直线的斜率k与相应的应力集中系数α用一元二次方程进行拟和,得到经验式:
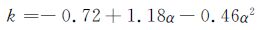
|
(5) |
可见,应力驱动对氢扩散的影响可分为3种情况:(1)当α=1.0时,斜率为0,随外加应力的增大,局部氢浓度不发生改变;(2)当α>1.0时,斜率为正,随应力的增大,氢浓度随之增大;(3)当α<1.0,斜率为负,随应力的增大,氢浓度反而降低。
|
图 5 氢浓度与应力集中系数的关系 (a)在应力分布图上设定分析路径Path 4;(b)在氢分布图上设定与应力相同的分析路径;(c)不同外加应力下的局部应力的变化;(d)局部应力对局部氢浓度的影响;(e)应力集中系数与斜率(氢浓度与应力的线线关系)的拟合关系曲线 Fig. 5 Relationship between hydrogen concentration and stress concentration (a)Path 4 was set in stress distribution map;(b)Path 4 was set in hydrogen distribution map as same as that in fig.(a);(c) the change curve of local stress under different applied load;(d)the effect of local stress change on local hydrogen concentration;(e) the fitted curve of stress concentration and slope of hydrogen concentration related to stress |
因此,局部氢浓度的大小由各区域的应力集中系数和应力水平决定。
3.4 氢脆断口形貌及解理裂纹的EBSD实验分析在快速渗氢溶液和大气中进行的慢拉伸力学性能实验结果如表 1所示,快速渗氢溶液中的试样断后伸长率为0,断裂强度仅为677MPa,低于大气中的材料屈服强度850MPa,说明材料尚未发生宏观塑性变形就已断裂,断口微观形貌如图 6(a)所示,为穿晶准解理的脆性断裂形态[22],同一Block板条束内的板条断裂形态相同,氢脆断口以Block板条束为结构单元发生穿晶断裂。大气环境下的无氢正常拉伸试样断口有塑性颈缩,断后伸长率达到14%,抗拉强度为1034MPa,试样在屈服极限以上发生塑性断裂,微观断口如图 6(b)所示,为韧窝断裂形态。对比上述两种断口形态可知,是氢引发了渗氢溶液中试样断裂的脆性转变。
| Environment | Rm/MPa | Rp0.2/MPa | A/% |
| Hydrogen permeation solution | 677 | — | 0 |
| Atmosphere | 1034 | 850 | 14 |

|
图 6 慢拉伸断口分析 (a)氢损伤环境下的脆性准解理断口;(b)大气下的韧窝断口 Fig. 6 Fracture surface analysisof specimen get by slow tensile test (a) the quasi-cleavage fracture morphology under hydrogen damage environment;(b) the dimple fracture morphology under atmosphere |
远离断口的剖面金相上可观察到3条微裂纹,裂纹两侧没有明显塑性变形,呈现氢脆裂纹的脆性开裂特征。对裂纹附近的组织进行EBSD分析。如图 7(a)所示,可见裂纹主要在弹性刚度差异大的板条处萌生,垂直于裂纹作两个分析路径Path 5,Path 6,弹性刚度的变化曲线如图 7(b)所示,裂纹附近的弹性刚度相差较大,在120GPa左右。依据EBSD实验得到的微区弹性刚度数据对该区域进行微区应力和氢浓度的模拟计算分析,结果如图 7(c),(d)所示,最大应力和最大氢浓度出现的位置与裂纹的产生区域相符,说明裂纹从氢的聚集区萌生,并扩展形成脆性裂纹。

|
图 7 氢脆裂纹区域的EBSD及数值模拟计算分析 (a)氢脆裂纹附近的弹性刚度分布;(b)沿Path 5,6的弹性刚度变化曲线;(c)施加横向载荷时的微区应力分布;(d)施加横向载荷时的氢浓度分布 Fig. 7 EBSD analysis on crack region and numerical simulation calculation (a)the elastic stiffness distribution for the HB crack region;(b)the change curve of elastic stiffness along Path 5 and Path 6;(c)the stress distribution applied by the load of TD direction;(d)the hydrogen concentration distribution by the load of TD direction |
板条马氏体结构钢依据其尺寸和显微组织形态,由大到小可划分[23-25]为原奥氏体晶粒、Packet板条束、Block板条束和Lath板条。同一Block板条束内的各Lath板条由于取向基本一致,其弹性刚度相差较小,不会形成明显的应力集中和氢的局部富集。相邻Block板条束的晶体取向不同,板条束间会形成弹性刚度梯度。弹性刚度梯度和组织尺寸越大,Block板条束的应力集中越严重,氢的局部富集浓度越高。
由于Block板条束的晶体取向和性能的各向异性,材料在微观下变形不均匀,微区应力分布主要受Block板条束之间的相互作用的影响,原奥氏体晶界和Packet晶界并不是微区应力集中的特殊位置。氢的扩散由应力主导时,氢会脱离这些晶界氢陷阱,向内部Block板条束应力集中处富集,引发穿晶开裂。这也是许多高温回火的马氏体组织结构钢在进行应力控制下的氢脆实验时,通常并不是以沿晶方式断裂,而是以穿晶准解理方式断裂的原因。但如果氢的扩散不完全由应力控制,或者原奥氏体或Packet晶界的碳化物或杂质偏析较为严重,氢在晶界陷阱处的优先富集会最终引发沿晶开裂。
4.2 应力集中系数对氢扩散的影响上述实验与模拟计算分析表明,马氏体微观组织的弹性刚度呈各向异性,外加应力作用时,应变及氢浓度在不同弹性刚度的组织单元上呈不均匀分布,形成局部应力集中及氢的局部富集。氢的富集程度由应力集中系数和应力大小决定。
弹性刚度梯度大且组织粗大的Block板条束,容易形成较大的应力集中。氢沿应力梯度方向扩散,向应力集中区富集。氢的局部富集程度主要由应力集中系数和应力水平决定:应力集中系数大于1时,氢浓度随应力的增大而增大;应力集中系数小于1时(即局部应力低于平均应力),氢浓度随应力的增大而减少。
应力对氢扩散的驱动现象可用相关文献在实验基础上得到的氢扩散经验式[26]进行解释:
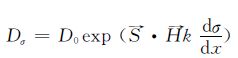
|
(6) |
式中:Dσ为应力梯度下的扩散系数;D0为应力梯度为零时的扩散系数;dσ/dx为应力梯度;k为常数;S表示应力梯度方向,H表示氢扩散方向,S·H=1时,表示氢扩散方向与应力梯度相同,S·H=-1时,表示氢扩散方向与应力梯度相反。
对应力集中系数大于1的区域,dσ/dx为正,氢扩散方向与应力梯度方向相同,外加应力越大,氢溶入的扩散系数也越大,氢浓度随应力的增大而增大;对应力集中系数小于1的区域,dσ/dx为负,氢扩散方向与应力梯度方向相反,外加应力越大,氢逸出的扩散系数也越大,氢浓度随应力的增大反而降低。此现象与本研究的数值结果相符。
5 结论(1) 由于板条马氏体中Block板条束的弹性刚度各向异性,有外力作用时,应力及氢浓度在微观组织下呈不均匀分布。
(2) 可以利用弹性刚度的各向异性计算马氏体组织的微区应力,Block板条束是表征微区应力的组织单元。
(3) 在应力驱动氢扩散的条件下,氢逐渐向高应力处扩散,使高应力区的Block板条束的氢浓度逐渐增加,低应力区的Block板条束的氢浓度逐渐降低。
(4) 马氏体组织的局部氢浓度主要取决于应力集中系数和应力水平,其中应力集中系数决定了氢浓度增大或减少的变化趋势。
(5) 弹性刚度梯度大以及组织粗大的Block板条束组织单元应力集中较为严重,聚集较高含量的氢,易萌生氢脆裂纹。
| [1] | 李永德, 徐娜, 郭卫民, 等. 高压气相热充氢对SUJ2轴承钢超高周疲劳行为的影响[J]. 材料工程,2014 (2) : 87 –98. LI Y D, XU N, GUO W M, et al. The influence of high pressure thermal hydrogen charging on very high cycle fatigue behavior of SUJ2 bearing steel[J]. Journal of Materials Engineering,2014 (2) : 87 –98. |
| [2] | AKIHIDE N, SHIGERU K, KOJI I, et al. Visualization of hydrogen transport in high strength steels affected by stress fields and hydrogen trapping[J]. Scripta Materialia,2001, 45 (10) : 1227 –1232. DOI: 10.1016/S1359-6462(01)01154-X |
| [3] | 郭昀静, 王春芳, 李建锡, 等. 利用TDS研究二次硬化钢中氢的扩散行为[J]. 航空材料学报,2012, 32 (3) : 5 –9. GUO Y J, WANG C F, LI J X, et al. Investigation of hydrogen diffusion in secondary hardening steel by means of thermal desorption spectrometry[J]. Journal of Aeronautical Materials,2012, 32 (3) : 5 –9. |
| [4] | ZHANG W S, HOU M Q, WANG H Y, et al. Numerical simulation of diffusivity of hydrogen in thin tubular metallic membranes affected by self-stresses[J]. International Journal of Hydrogen Energy,2004, 29 (11) : 1165 –1172. |
| [5] | KIMURA Y, SAKAI Y, HARA T, et al. Hydrogen induced delayed fracture of ultrafine grained 0. 6%O steel with dispersed oxide particles[J]. Scripta Materialia,2003, 49 (11) : 1111 –1116. DOI: 10.1016/j.scriptamat.2003.08.006 |
| [6] | HARDIE D, LIU S E. The effect of stress concentration on hydrogen embrittlement of a low alloy steel[J]. Corrosion Science,1996, 38 (5) : 721 –733. DOI: 10.1016/0010-938X(96)00161-8 |
| [7] | WANG M Q, AKIYAMA E, TSUZAKI K. Determination of the critical hydrogen concentration for delayed fracture of high strength steel by constant load test and numerical calculation[J]. Corrosion Science,2006, 48 (8) : 2189 –2202. DOI: 10.1016/j.corsci.2005.07.010 |
| [8] | BARNOUSH A, VEHOFF H. Recent development in the study of hydrogen embrittlement:hydrogen effect on dislocation nucleation[J]. Acta Materialia,2010, 58 (16) : 5274 –5285. DOI: 10.1016/j.actamat.2010.05.057 |
| [9] | DOSHIDA T, NAKAMURA M, SAITO H, et al. Hydrogen-enhanced lattice defect formation and hydrogen embrittlement of cyclically prestressed tempered martensitic steel[J]. Acta Materialia,2013, 61 (20) : 7755 –7766. DOI: 10.1016/j.actamat.2013.09.015 |
| [10] | NEERAJ T, SRINIVASAN R, LI J. Hydrogen embrittlement of ferritic steels:observations on deformation microstructure, nanoscale dimples and failure by nanovoiding[J]. Acta Materialia,2012, 60 (13) : 5160 –5171. |
| [11] | ZHAO M J, GUO Z F, CHEN S H, et al. Hydrogen-induced modification in the deformation and fracture of a precipitation-hardened Fe-Ni based austenitic alloy[J]. Journal of Materials Science & Technology,2014, 30 (11) : 1155 –1159. |
| [12] | VENEGAS V, CALEYO F, GONZÁLEZ J L, et al. EBSD study of hydrogen induced cracking in API-5-5L-X46 pipeline steel[J]. Scripta Materialia,2005, 52 (2) : 147 –152. DOI: 10.1016/j.scriptamat.2004.09.015 |
| [13] | LIM H, LEE M G, KIM J H, et al. Simulation of polycrystal deformation with grain and grain boundary effects[J]. International Journal of Plasticity,2011, 27 (27) : 1328 –1354. |
| [14] | TUNG P V, KATJA J, THOMAS B. Simulation of sheet metal forming incorporating EBSD data[J]. Journal of Materials Processing Technology,2012, 212 (12) : 2659 –2668. DOI: 10.1016/j.jmatprotec.2012.07.015 |
| [15] | NYE J F. Physical Properties of Crystals[M]. London: Oxford University Press, 1985 . |
| [16] | THOMAS J H, BRENT L A, DAⅥD T F, et al. Estimation of the full Nye's tensor and its gradients by micro-mechanical stereo-inference using EBSD dislocation microscopy[J]. International Journal of Plasticity,2013, 50 : 146 –157. DOI: 10.1016/j.ijplas.2013.04.006 |
| [17] | MURA T. Micromechanics of Defects in Solid[M]. Dordrecht, Holland: Matrinus Nijhoff Publishers, 1987 . |
| [18] | LUFRANO J, SOFRONIS P. Enhanced hydrogen concentrations ahead of rounded notches and cracks-competition between plastic strain and hydrostatic stress[J]. Acta Materialia,1998, 46 (5) : 1519 –1526. DOI: 10.1016/S1359-6454(97)00364-9 |
| [19] | ZAKROCZYMSKI T, OWCZAREK E. Electrochemical investigation of hydrogen absorption in a duplex stainless steel[J]. Acta Materialia,2002, 50 (10) : 2701 –2713. DOI: 10.1016/S1359-6454(02)00105-2 |
| [20] | 褚武扬. 氢损伤和滞后断裂[M]. 北京: 冶金工业出版社, 1988 . CHU W Y. Hydrogen Induced Cracking and Delayed Fracture[M]. Beijing: Metallurgical Industry Press, 1988 . |
| [21] | 孙秦, 童小燕, 杨庆雄. 多晶体材料微结构弹性性质的数值统计分析[J]. 机械强度,1997, 19 (1) : 37 –41. SUN Q, TONG X Y, YANG Q X. Numerical statistical analysis on elastic behaviors of polycrystalline material microstructures[J]. Journal of Mechanical Strength,1997, 19 (1) : 37 –41. |
| [22] | AKIHIDE N, CYNTHIA D S, MOHSEN D, et al. The role of hydrogen in hydrogen embrittlement fracture of lath martensitic steel[J]. Acta Materialia,2012, 60 (13-14) : 5182 –5189. DOI: 10.1016/j.actamat.2012.06.040 |
| [23] | MORITO S, TANAKA H, KONISHI R, et al. The morphology and crystallography of lath martensite in Fe-C alloys[J]. Acta Materialia,2003, 51 (6) : 1789 –1799. DOI: 10.1016/S1359-6454(02)00577-3 |
| [24] | YOJI M, KOICHI H, HIROKI T, et al. Micro-tension behavior of lath martensite structures of carbon steel[J]. Materials Science and Engineering,2013, 560 (10) : 535 –544. |
| [25] | KITAHARA H, UEJI R, UEDA M, et al. Crystallographic features of lath martensite in low-carbon steel[J]. Acta Materialia,2006, 54 (5) : 1279 –1288. DOI: 10.1016/j.actamat.2005.11.001 |
| [26] | 权高峰, 宋余九. 应力场中氢扩散的实验研究[J]. 中国腐蚀与防护学报,1993, 13 (1) : 80 –85. QUAN G F, SONG Y J. An experimental study on hydrogen diffusion in stress fields[J]. Journal of Chinese Society for Corrosion and Protection,1993, 13 (1) : 80 –85. |
 2016, Vol. 44
2016, Vol. 44


