文章信息
- 张伟, 马志远, 赫丽华, 高剑英, 罗文, 林莉, 雷明凯
- ZHANG Wei, MA Zhi-yuan, HE Li-hua, GAO Jian-ying, LUO Wen, LIN Li, LEI Ming-kai
- 基于声压反射系数幅度谱匹配分析的薄层厚度和超声纵波声速双参数反演
- Simultaneous Inversion of Thickness and Ultrasonic Longitudinal Velocity for Thin Layered Structure Based on Ultrasonic Reflection Coefficient Amplitude Spectrum Matching Analysis
- 材料工程, 2016, 44(10): 74-79
- Journal of Materials Engineering, 2016, 44(10): 74-79.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2016.10.011
-
文章历史
- 收稿日期: 2016-01-28
- 修订日期: 2016-07-08
2. 北京航空材料研究院, 北京 100095
2. Beijing Institute of Aeronautical Materials, Beijing 100095, China
薄层材料已广泛应用于航空航天等诸多领域,如航空发动机热障涂层、可磨耗封严涂层、先进战机表面涂装的雷达吸波涂层等。在表征薄层材料性能的各项指标中,厚度不仅是表征薄层材料自身尺寸的几何参量,而且对薄层材料的性能和使用寿命也有重要影响[1-6]。例如,在吸波涂层设计和涂装过程中,如果涂层厚度达不到或超过设计值都无法实现预定的吸波效果,而且厚度过大或不均匀还会降低其结合强度和使用寿命,引起涂层塑性变差甚至导致局部剥落。因此,采用无损检测技术对厚度进行准确测量已成为保证薄层材料性能的重要手段。
现有的无损检测技术中,超声脉冲回波技术由于具有原理明确、实现简单、适用范围广等优点,已广泛应用于层状介质材料的厚度测量之中[7, 8]。但对于薄层材料,超声波在薄层中的传播时间小于其脉冲宽度,薄层表面波和界面波将会发生混叠。同时,由于受到工艺参数、薄层非均质性等因素的影响,薄层的纵波声速往往为未知且在不同位置存在一定的波动[9]。这些问题都为薄层厚度的超声检测带来了困难。Haines等[10]提出利用垂直入射条件下的声压反射系数幅度谱分析方法对铝基体表面涂覆的环氧树脂层厚度进行测量,实现了混叠信号中超声特征参量的提取,但该方法将薄层纵波声速设为常数,未考虑非均质性引起的声速波动,难以用于非均质薄层厚度的测量。赵扬等[11]提出采用高斯-牛顿法对非均质热障涂层厚度和超声纵波声速进行反演,该方法具有局部收敛速度快、匹配精度高等优点,但对初始值的选取要求较高,如果初始值选取不当就可能导致只收敛到局部最优解甚至方程不收敛,无法得到反演结果。
本工作在已有研究的基础上,首先利用声压反射系数幅度谱分析方法实现混叠信号中超声特征参量的提取,有效解决了薄层中超声信号混叠导致超声特征参量无法提取的问题。随后,引入统计学中的相关系数匹配法,对薄层试样实测声压反射系数幅度谱和理论声压反射系数幅度谱矩阵在超声检测有效频带范围内逐一进行匹配分析,通过计算相关系数最大值点对应的反演参数获得薄层厚度和纵波声速的最佳匹配结果,实现了超声纵波声速未知及非均质薄层声速波动条件下薄层厚度的测量,避免了现有高斯-牛顿法由于反演初始值选取不当导致迭代发散、无法获得反演结果的问题。
1 原理与方法声压反射系数幅度谱(URCAS)[11-15]分析方法是一种适用于薄层介质材料超声检测的信号后处理技术,其核心思想是利用回波信号的声压反射系数幅度谱信息提取出与被检材料特性相关的超声特征参量,实现材料特性的超声表征。公式(1)为超声波垂直入射条件下,薄层的声压反射系数幅度谱表达式[11]:
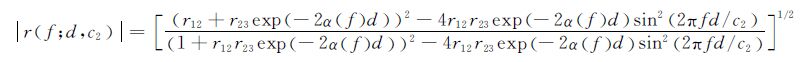
|
(1) |
式中:下角1,2,3分别代表探头延迟块、薄层和基底材料;r12,r23为异质材料界面的声压反射系数;d为薄层厚度;c2和α(f)分别为薄层的声速和声衰减系数。
探头接收到的回波信号实际上是声波经过多次反射和透射后综合叠加的结果。超声波在薄层结构中多次反射过程中,频率为fn的信号将发生干涉,导致声压反射系数幅度谱上出现多个极大值或极小值,对(1)式频率f求导,当导数为零时得到URCAS的一系列极值点:
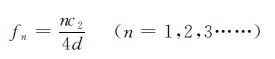
|
(2) |
式中fn和n分别为谐振频率和谐振频率阶数。
因此,当薄层纵波声速已知时,利用幅度谱上极值点的位置坐标,通过(2)式即可测得薄层厚度。但由于受到工艺参数、薄层非均质性等因素的影响,薄层声速通常为未知量且在不同位置存在一定的波动。如果探头延迟块及基底材料的声速、密度,薄层的密度和声衰减系数α(f)已知,公式(1)就变成了以薄层厚度d和纵波声速c2为自变量的二元非线性方程,采用合适的方法对此方程进行求解,即可实现d和c2的双参数同时表征。
本工作从参数反演的角度出发提出采用统计学中的相关系数匹配法对涂层厚度和纵波声速进行表征。相关系数匹配法是以相关系数为匹配测度判断两组数据相似性的统计学方法,相关系数越大说明二者的相似度越高。常用的皮尔逊积矩相关系数定义如下[16]:
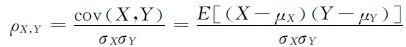
|
(3) |
式中:ρX,Y为总体相关系数;σX,σY为变量X,Y的标准差;μX,μY为X,Y的期望。基于样本对协方差和标准差进行估计,可以得到样本相关系数:
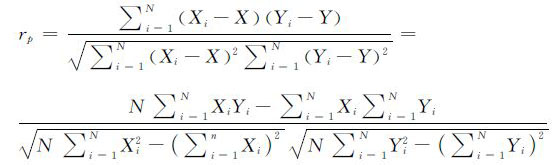
|
(4) |
利用式(4)对实测得到的反射系数幅度谱|r(f)|和理论计算得到的反射系数幅度谱|r(f)|*在-6dB有效频带内进行匹配分析:
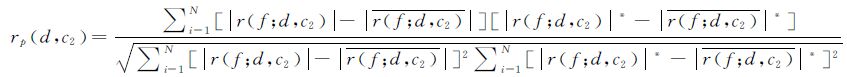
|
(5) |
式中:N表示时域信号经FFT变换后有效频带范围内的数据点数;下角标i表示第i个频率值;|rf;d,c2|与|rf;d,c2|*分别为有效频带内实测与理论的声压反射系数幅度谱;|rf;d,c2|与|rf;d,c2|*分别为有效频带内实测与理论的声压反射系数幅度谱的算术平均值。
通过赋予吸波涂层厚度d和纵波声速c2一系列连续变化值,得到理论声压反射系数幅度谱矩阵,令其作为母体,将实测的声压反射系数幅度谱与其逐一进行匹配分析,相关系数矩阵中最大位置对应的d和c2即为被测试样涂层厚度与纵波声速的最佳反演结果。
2 实验 2.1 实验样品实验选用的样品为空气喷涂法制备的雷达吸波涂层试样,吸收剂类型为羰基铁粉,黏结剂主要成分为环氧树脂,基底材料为铝合金平板。吸波涂层厚度约为0.2mm,吸波涂层试样的材料属性如表 1所示。其中,铝合金基底材料的声速由超声渡越时间法测得,涂层和铝合金的密度采用阿基米德排水法测定,涂层声衰减系数由实测数据采用最小二乘法拟合得到。
| Material | Velocity/ (m·s-1) | Density/ (kg·m-3) | Attenuation coefficient/ (dB·mm-1) |
| RAC | — | 3290.0 | α(f)=1.47f+ 8.51×10-4f4 |
| Aluminum alloy | 6480.0 | 2700.0 | — |
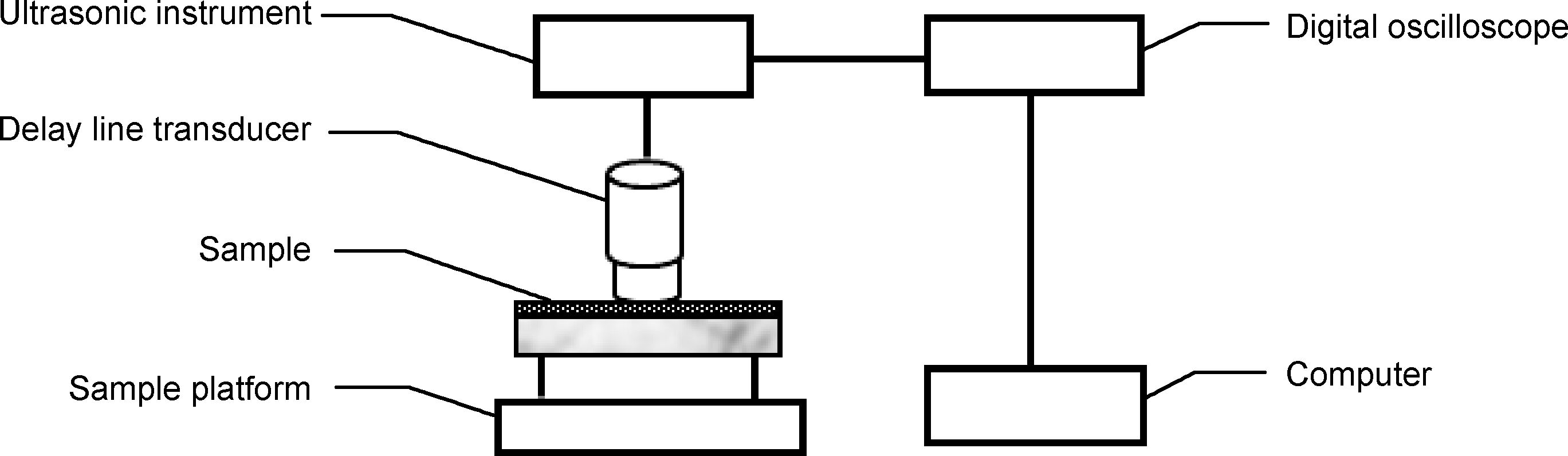
超声脉冲回波检测系统连接示意图如图 1所示。实验中采用延迟块探头作为超声信号收发装置,探头晶片直径6mm,中心频率5MHz。延迟块材料为环氧树脂,纵波声速2316.6m/s,密度1045.5kg/m3。使用USIP40超声波探伤仪激发探头,DPO4032数字示波器以及计算机完成超声信号的观察、数据采集和反演分析工作。
|
图 1 超声检测系统连接示意图 Fig. 1 Sketch of ultrasonic testing system |
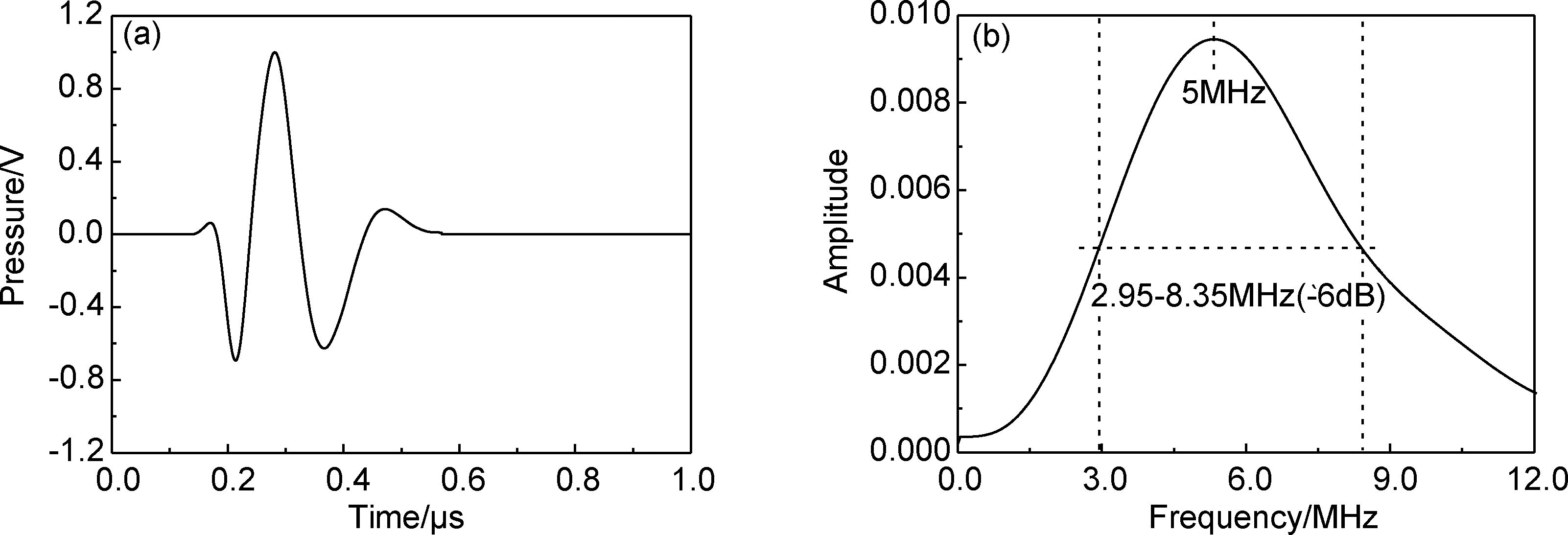
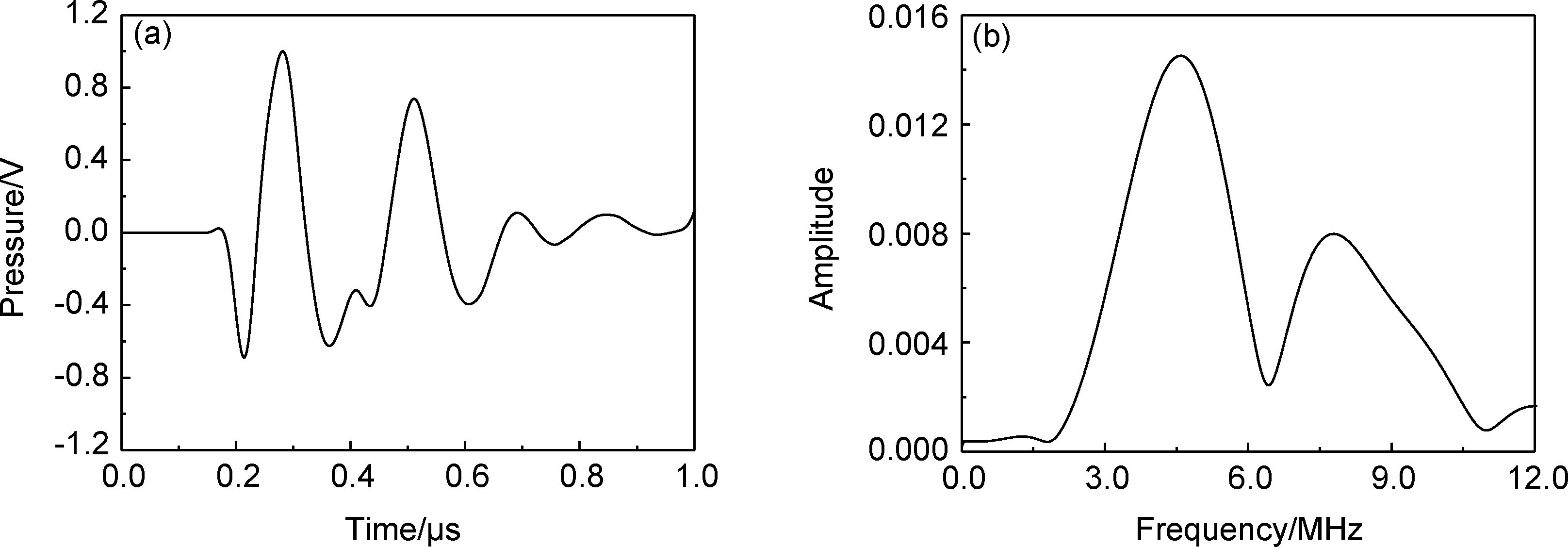
实验过程中首先将延迟块探头连接到探伤仪进行系统与仪器校正。通过DPO4032数字示波器采集的声源时域波形,其中心频率为5MHz,幅度谱-6dB有效频带宽为2.95~8.35MHz,如图 2所示。将探头耦合到吸波涂层试样上,采集到的涂层试样时域回波信号和幅度谱如图 3所示。
|
图 2 5MHz声源时域信号 (a)及其幅度谱(b) Fig. 2 Time-domain signal of 5MHz acoustic source (a) and its amplitude spectrum (b) |
|
图 3 吸波涂层时域回波信号 (a)及其幅度谱(b) Fig. 3 Time-domain signal reflected from RAC (a) and its amplitude spectrum (b) |
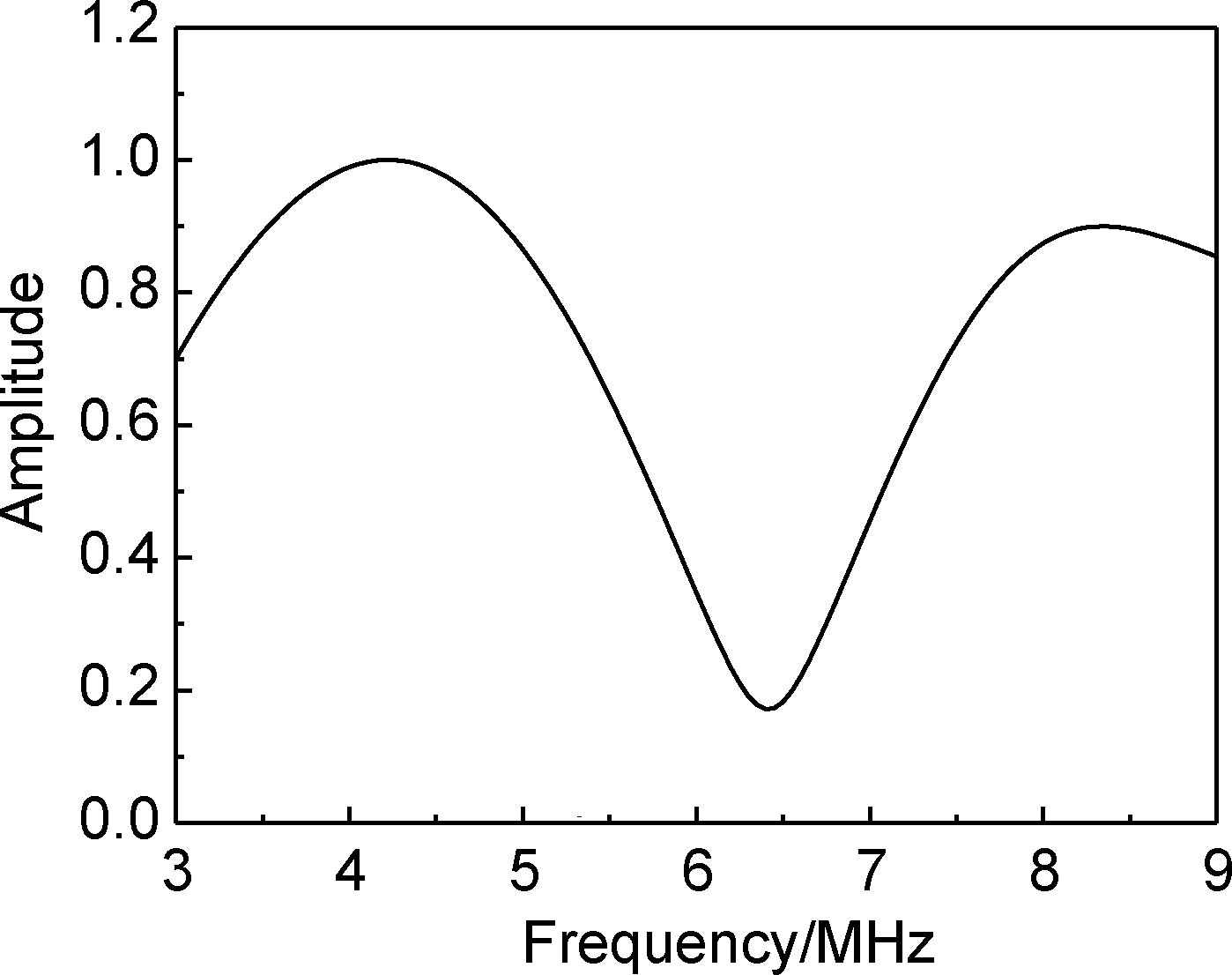
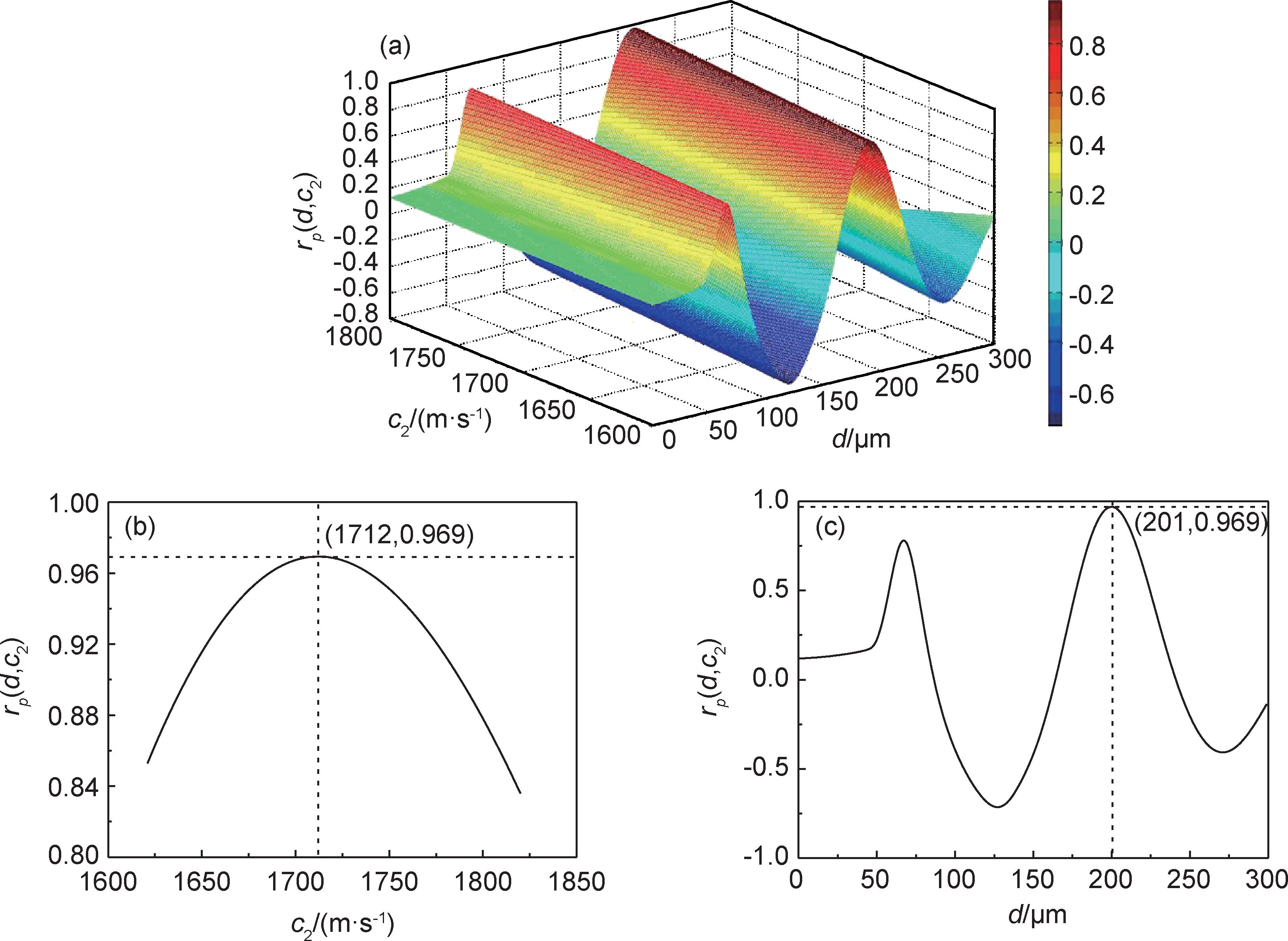
对超声检测实验中采集到的吸波涂层时域回波信号进行频谱分析处理,获得吸波涂层的实测声压反射系数幅度谱,利用相关系数匹配法对实验得到的反射系数幅度谱|r(f)|(见图 4)和理论计算得到的反射系数幅度谱|r(f)|*在-6dB有效频带内进行匹配分析,反演结果如图 5所示,通过读取图中相关系数rp(d,c2)的最大值位置的坐标,即可确定出涂层厚度和纵波声速的最佳反演结果。
|
图 4 吸波涂层实测声压反射系数幅度谱 Fig. 4 The experimental URCAS of RAC |
|
图 5 吸波涂层相关系数计算结果 (a)rp(d,c2)-d-c2三维视图;(b)rp(d,c2)-c2 二维曲线;(c)rp(d,c2)-d二维曲线 Fig. 5 Correlation coefficient calculation results of RAC (a)3D view of rp(d,c2)-d-c2;(b)two-dimensional projection of rp(d,c2)-c2;(c)two-dimensional projection of rp(d,c2)-d |
同理,将延迟块探头耦合到试样的其他位置重复上述步骤,反演结果及测量误差如表 2所示,涂层厚度反演结果与千分尺测量得到的真实值间绝对误差为5~8μm、相对误差为2.53%~3.72%,纵波声速与真实值间绝对误差为4.3~6.4m/s、相对误差为2.51%~3.75%,满足工程检测要求。图 6为涂层试样实测与最佳匹配位置理论声压反射系数幅度谱的对比曲线,可以发现二者在低频段范围内符合较好,但随着频率的增加二者的偏离程度逐渐增大。分析认为,这是由于涂层理论声压发射系数幅度谱中密度和衰减系数采用的是涂层试样整体平均测量结果,并未充分考虑吸波涂层非均质性引起的密度和声衰减系数在不同位置存在波动的问题,导致理论谱线发生偏离,带来一定的反演误差。
| Measurement point | dture/μm | c2ture/(m·s-1) | dest/μm | c2est/(m·s-1) | εd/% | εc2/% |
| 1 | 195 | 1717.1 | 201 | 1712.0 | 3.08 | 2.97 |
| 2 | 198 | 1712.8 | 203 | 1708.5 | 2.53 | 2.51 |
| 3 | 204 | 1708.4 | 211 | 1702.0 | 3.43 | 3.75 |
| 4 | 215 | 1703.7 | 223 | 1699.0 | 3.72 | 2.76 |
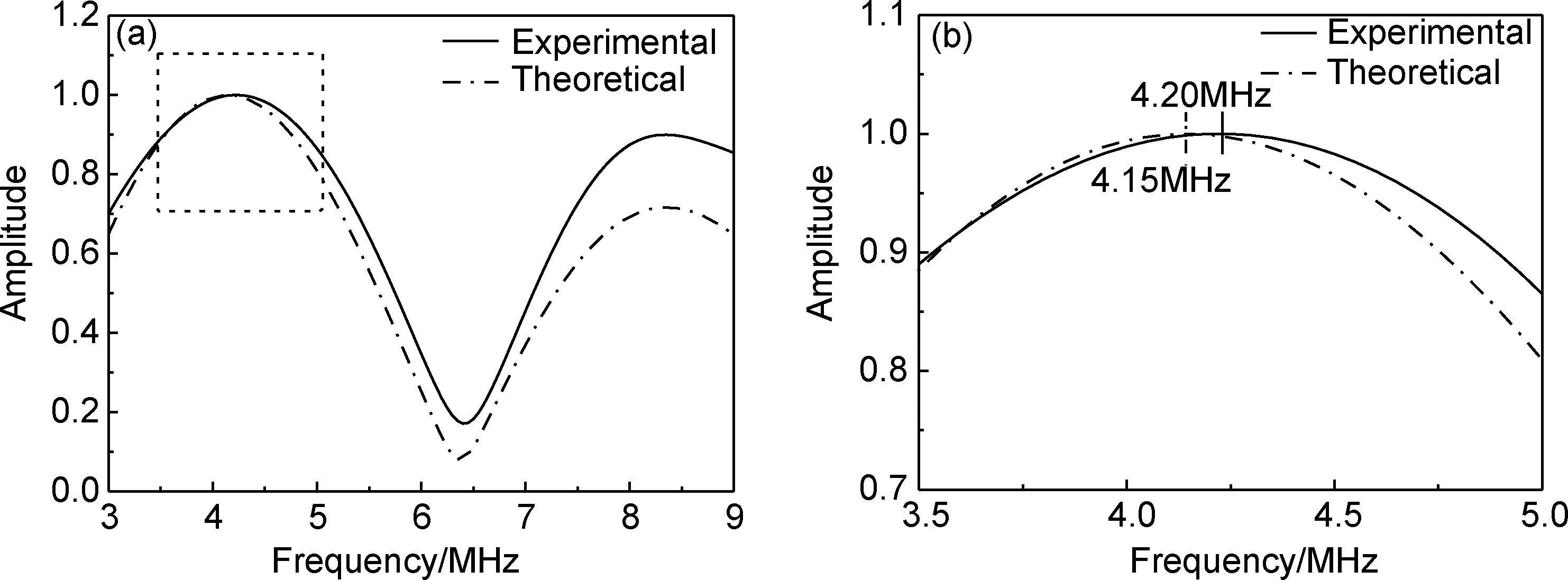
|
图 6 吸波涂层实测与理论声压反射系数幅度谱对比 (a)及其局部放大(b) Fig. 6 Comparison of experimental and theoretical URCAS of RAC (a) and partial enlarged drawing (b) |
(1) 从参数反演的角度,提出采用相关系数匹配法对薄层试样实测和理论声压反射系数幅度谱逐一进行匹配分析,无需已知薄层超声纵波声速即可实现薄层厚度和纵波声速的同时表征,解决了薄层厚度和纵波声速均为未知情况下薄层厚度的测量问题。
(2) 利用本方法反演得到的吸波涂层厚度与实际测量值间最大绝对误差为8μm、最大相对误差为3.72%,纵波声速与实测值间最大绝对误差为6.4m/s、最大相对误差为3.75%。
(3) 本方法不仅适用于雷达吸波涂层的厚度测量,还可应用于航空发动机热障涂层、可磨耗封严涂层等其他非均质薄层材料,具有良好的推广和应用前景。
| [1] | QU C C, LI J, BAI L L, et al. Effects of the thickness of the pre-placed layer on microstructural evolution and mechanical properties of the laser-clad coatings[J]. Journal of Alloys and Compounds,2015, 644 : 450 –463. DOI: 10.1016/j.jallcom.2015.05.081 |
| [2] | CARVALHO P, SAMPAIO P, AZEVEDO S, et al. Influence of thickness and coatings morphology in the antimicrobial performance of zinc oxide coatings[J]. Applied Surface Science,2014, 307 (10) : 548 –557. |
| [3] | PLOYPECH S, JEARANAISILAWONG P, BOONYONGMANEERAT Y. Influence of thickness of intermetallic layers on fracture resistance of galvanized coatings[J]. Surface and Coatings Technology,2013, 223 (6) : 1 –5. |
| [4] | 赫丽华, 刘平桂, 王晓红. 雷达吸波涂层的失效行为[J]. 失效分析与预防,2009, 4 (3) : 182 –187. HE L H, LIU P G, WANG X H. Degeneration behavior of radar absorbing coatings[J]. Failure Analysis and Prevention,2009, 4 (3) : 182 –187. |
| [5] | 韩萌, 黄继华, 陈树海. 热障涂层应力与失效机理若干关键问题的研究进展与评述[J]. 航空材料学报,2013, 33 (5) : 83 –98. HAN M, HUANG J H, CHEN S H. Research progress and review on key problems of stress and failure mechanism of thermal barrier coating[J]. Journal of Aeronautical Materials,2013, 33 (5) : 83 –98. |
| [6] | MORIDI A, AZADI M, FARRAHI G H. Thermo-mechanical stress analysis of thermal barrier coating system considering thickness and roughness effects[J]. Surface and Coatings Technology,2014, 243 (4) : 91 –99. |
| [7] | MAEV R G, SHAO H, MAEVA E Y. Thickness measurement of a curved multilayered polymer system by using an ultrasonic pulse-echo method[J]. Materials Characterization,1998, 41 (2-3) : 97 –105. DOI: 10.1016/S1044-5803(98)00030-8 |
| [8] | MVLLER H, SCHALLER N, EGER T. Ultrasonic determination of thickness of masticatory mucosa:a methodologic study[J]. Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology, and Endodontology,1999, 88 (2) : 248 –253. DOI: 10.1016/S1079-2104(99)70123-X |
| [9] | 马志远, 罗忠兵, 林莉. 基于RVM表征热障涂层孔隙率与孔隙形貌对超声纵波声速的影响[J]. 材料工程,2014 (5) : 86 –90. MA Z Y, LUO Z B, LIN L. Characterization of ultrasonic longitudinal velocity evolution in TBCs with different porosity and void morphology based on random void model[J]. Journal of Materials Engineering,2014 (5) : 86 –90. |
| [10] | HAINES N F, BELL J C, MCINTYRE P J. The application of broadband ultrasonic spectroscopy to the study of layered media[J]. The Journal of the Acoustical Society of America,1978, 64 (6) : 1645 –1651. DOI: 10.1121/1.382131 |
| [11] | ZHAO Y, LIN L, LI X M, et al. Simultaneous determination of the coating thickness and its longitudinal velocity by ultrasonic nondestructive method[J]. NDT & E International,2010, 43 (7) : 579 –585. |
| [12] | LI J C, LIN L, LI X M, et al. Ultrasonic characterization of modified Cr2O3 coatings by reflection coefficient spectroscopy[J]. Transactions of Nonferrous Metals Society of China,2010, 20 (3) : 418 –424. DOI: 10.1016/S1003-6326(09)60156-4 |
| [13] | CONG S, GANG T. Ultrasonic thickness measurement for aluminum alloy irregular surface parts based on spectral analysis[J]. Transactions of Nonferrous Metals Society of China,2012, 22 (2) : 323 –328. |
| [14] | LIN L, ZHAO Y, LI X M, et al. Ultrasonic characterization of EB-PVD thermal barrier coatings irradiated by HIPIB[J]. Key Engineering Materials,2008 : 373-374 –358-362. |
| [15] | MA Z Y, ZHAO Y, LUO Z B, et al. Ultrasonic characterization of thermally grown oxide in thermal barrier coating by reflection coefficient amplitude spectrum[J]. Ultrasonics,2014, 54 (4) : 1005 –1009. DOI: 10.1016/j.ultras.2013.11.012 |
| [16] | 朱永松, 国澄明. 基于相关系数的相关匹配算法的研究[J]. 信号处理,2003, 19 (6) : 531 –534. ZHU Y S, GUO C M. The research of correlation matching algorithm based on correlation coefficient[J]. Journal of Signal Processing,2003, 19 (6) : 531 –534. |
 2016, Vol. 44
2016, Vol. 44


