文章信息
- 张海军, 周储伟
- ZHANG Hai-jun, ZHOU Chu-wei
- 基于显微CT图像的细编穿刺碳/碳复合材料细观力学模型
- Meso-mechanical Model on Fine Weave Pierced C/C Composites Based on Micro Computed Tomography
- 材料工程, 2016, 44(5): 65-71
- Journal of Materials Engineering, 2016, 44(5): 65-71.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2016.05.011
-
文章历史
- 收稿日期: 2014-11-21
- 修订日期: 2015-03-26
C/C复合材料是以碳纤维增强碳基体的复合材料,具有耐高温、密度小、烧蚀均匀和耐摩擦等特性,因此在航空航天、核能及许多民用工业领域受到了广泛关注[1, 2]。C/C复合材料的制备主要包括预制体的成型、致密化处理和石墨化[3, 4]等步骤,受工艺限制,基体和纤维束中存在密度不均匀、孔隙和微裂纹等缺陷。
大量研究证明C/C复合材料的细观结构及微缺陷对其性能有显著影响。Siron和Lamon[5]实验观察了缎纹织物增强C/C复合材料基体中孔隙、微裂纹在拉伸和剪切载荷下的扩展,发现这些损伤发展最终使得材料拉伸模量下降了25%,剪切模量下降了80%。Blanco等[6]采用油浸显微镜观察了单丝和单丝界面,通过断裂实验的断口分析,得出了界面层的强弱对材料的强度影响很大,强界面层使得材料表现出脆性破坏,反之则会呈现一定的塑性。Aly-Hassan等[7]研究了无纺正交织物增强C/C复合材料的强度,发现加载过程中,纤维/基体界面微裂纹长度增加,材料拉伸强度会下降60%。这类微缺陷还会直接影响其氧化过程。Han等[8]研究了细编C/C复合材料高温下的氧化,利用TEM和XRD观察发现氧化最先发生于材料表面和孔隙处,并且向内部以及孔隙周围扩展。Jacobson等[9]发现二维铺层C/C复合材料的高温氧化反应在涂层裂纹以及涂层下方碳基体孔隙处最先发生。
CT作为一种无损探测技术,可以进行密集的断层扫描,所以高分辨率的CT能完整地描述C/C复合材料内部结构细观特征[10, 11, 12]。国内外已有不少利用CT技术对C/C复合材料微细观结构进行研究的报道。Martín-Herrero等[13, 14]对C/C复合材料的显微CT图像进行了信息提取,通过邻近位置灰度差来判别各组分的边界,重构了C/C复合材料细观几何模型。但其方法要求各组分间具有较明晰的边界,对图像分辨率的要求很高,因此CT扫描工作量很大并且对设备要求高。阚晋[15]基于CT图像建立了C/C复合材料考虑基体孔隙的力学模型,但模型还是作了很多简化,诸如纱线的局部弯曲等因素没有考虑。
本工作对一种细编穿刺C/C复合材料的CT图片进行了二值化,提取了孔隙和纤维束局部弯曲的细观特征参数,建立了基于这些特征参数的力学模型,并进行了有效弹性模量的计算以及相应的实验验证。
1 CT图像及处理MATLAB软件在CT图像处理领域内有着广泛应用[16, 17, 18],本工作的图像也采用MATLAB处理。细编穿刺C/C复合材料试件的CT扫描工作是在Nano Voxel-2700显微CT机上完成,空间分辨率为30μm。局部结构如图 1所示,长方体边长X,Y和Z向尺寸分别是5.42,5.25mm和5mm。

|
图1 CT三维重构图 Fig.1 3D reconstruction image from CT |
选取YZ平面图像为例,进行Y向纤维束提取。由于基体材料和增强纤维材料都是碳元素,CT图像灰度非常接近,是典型的低对比度图像。常规的灰度值均匀化以及高斯小波等方法并不适用。针对C/C复合材料CT图片低对比度的特点,本工作发现利用合适的阈值进行组分边界的识别简单有效,继而提出阈值筛选的两步法:首先通过完整CT图像的灰度统计图,得出阈值的分布区间,然后再对比局部图像及其灰度矩阵,确定阈值。图 2(a)中,纤维束所占比例最大,且亮度最高,观察其灰度统计图,如图 3所示,纤维束的灰度分布在图右侧1/2,而150附近处的波谷,即为纤维束与周围介质的边界灰度,所以通过两步法的第一步,得出阈值分布在150附近。

|
图2 C/C复合材料CT原图(a)和局部放大图(b) Fig.2 CT images of C/C composite (a)original image; (b)local enlarged view image |

|
图3 C/C复合材料CT图像灰度值分布图 Fig.3 Gray level map of CT image of C/C composite |
然后在原图中取出包含纤维束边界的局部图像,如图 2(b)中左边界附近白框区域,其灰度矩阵如图 4所示,通过第一步确定的阈值范围,以及图 2(b)观察窗口中的纤维束边界,可以确定图 4中灰色标记即为纤维束与周围介质的边界。综合上述两步,选取150作为阈值。

|
图4 局部图形灰度值矩阵 Fig.4 Gray level value matrix of local |
通过两步法得出的阈值,对原CT图像进行纤维束组分的提取,生成仅包含X向纤维束的二值图,结果如图 5(a)所示,纤维束边界清晰,忠于原图,但图中还存在噪声和边界毛刺。本工作采用中值滤波,滤波模板采用5×5大小,降噪处理后如图 5(b)所示,图像中不再有噪声干扰,纤维束轮廓清晰,但局部边界处仍存有毛刺。对上述步骤所得的二值图,进行平滑处理,即利用适当算子进行腐蚀和膨胀操作。本工作选择“line,8×8”作为算子,腐蚀后的图像见图 5(c),边界光滑,但边界有损失,所以用同样的算子,进行一次膨胀操作,效果见图 5(d)。上述方法不仅可以得到Y向纤维束的二值图,同理可以得到X,Z两个方向纤维束以及孔隙的二值图。

|
图5 去噪声和平滑处理后的二值图 (a)边界提取后;(b)去噪声后;(c)腐蚀后;(d)膨胀后 Fig.5 Binary images after noises removal and boundaries smoothed (a)after boundaries extracted;(b)after noises removal;(c)after corrosion;(d)after inflation |
纤维束体积分数以及孔隙率,可以通过二值图的统计得出。例如图 6中孔隙的像素点数与总的像素点数之比,即可得到孔隙率。

|
图6 基体中的孔洞 Fig.6 Voids in matrix |
经过统计试件所有CT图像,得出复合材料平均孔隙率为4.8%,与材料称重测量的孔隙率4%~5%基本一致。同理统计计算得出复合材料X,Y和Z 方向纤维束的平均体积分数为11%,16%以及7.4%,纯基体体积分数为60.8%,进而得到基体中平均孔隙率为7.9%。基体中孔隙是随机分布的,通过对图像统计得出基体中孔隙体积分数的概率密度分布近似满足正态分布,如图 7所示,对其进行曲线拟合得出其期望μv=0.079,标准差σv=0.024。

|
图7 基体孔隙率的概率分布图 Fig.7 Probability distribution map of void volume fraction in matrix |
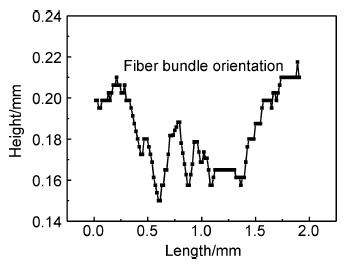
细编穿刺C/C复合材料预成形体在织造的过程中,因三个方向纤维束的相互挤压,会造成纤维束发生周期性的局部微弯曲,观察CT图像也证实这一点。综合纤维束三个方向的二值图像可发现,X向纤维束图像中心线的弯曲仅在XZ平面内比较明显,同样Y向纤维束也可仅考虑在YZ平面内的微弯曲。图 8给出了X向的单根纤维束在XZ面内的波动。纤维束的局部波动对复合材料面内力学性能的影响可以用平均偏角表征,平均偏角定义为图 8中相邻两点之间倾角的算术平均值。
|
图8 纤维束的局部波动 Fig.8 Local undulation of fiber bundles |
通过对所有CT图像分析,X方向和Y方向纤维束的偏角分布如图 9所示。

|
图9 X向(a)和Y向(b)纤维束偏角概率分布图 Fig.9 Probability distribution map of declinations of fiber bundles (a)X direction;(b)Y direction |
X向纤维束偏角近似视为正态分布,期望为μθX=5.29°,标准差σθX=1.54°。Y向纤维束偏角近似为Laplace分布,其期望μθY=10.08°,尺度参数bθY=0.86°。
3 复合材料细观力学模型假设C/C复合材料微孔隙缺陷都分布在纤维束之间的碳基体富集区,该区中材料的等效弹性常数仍是各向同性的,采用Mori-Tanaka模型[19, 20]计算基体的等效弹性模量Em和剪切模量Gm,它们和基体孔隙率Vvm(下标v是void,上标m是matrix)的关系为:

|
(1) |
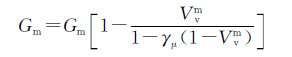
|
(2) |
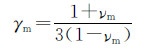
|
(3) |

|
(4) |
碳基体的弹性模量Em和泊松比νm分别取为11GPa和0.1[21]。根据第2节得到的基体孔隙率分布,使用MATLAB随机数生成器生成满足上述分布的20组基体孔隙率,计算得出相应的20组含孔隙基体的拉伸模量和剪切模量。发现其分布近似满足正态分布,拉伸模量的期望μEm=9.61GPa,标准差σEm=0.12GPa。剪切模量正态分布的期望μGm=4.26GPa,标准差σGm=0.063GPa。
由二值图统计得出纤维束经密(X向)和纬密(Y向)都为4束/厘米。X向和Y向纤维束包含两股3K纤维束,它们的平均截面积分别为0.29mm2和0.43mm2,Z向包含三股3K纤维束,平均截面积为0.52mm2,所以X,Y和Z向的纤维束的平均纤维体积分数分别为79.6%,53.7%以及65.8%。纤维束为横观各向同性材料,弹性常数可由纤维和基体两相材料经混合法计算得到[22]。本工作C/C复合材料所用纤维为T300纤维,弹性常数如表 1所示,根据各个方向纤维束中的纤维体积分数,计算得出等效弹性常数如表 2所示。
| Ef11/GPa | Ef22/GPa | νf12 | νf23 | Gf12/GPa |
| 230 | 15 | 0.02 | 0.25 | 9 |
| Direction | Ey11/GPa | Ey22/GPa | νy12 | νy23 | Gy12/GPa |
| X | 185.3 | 14.4 | 0.04 | 0.25 | 8.4 |
| Y | 128.6 | 13.7 | 0.06 | 0.23 | 7.7 |
| Z | 155.1 | 14.0 | 0.04 | 0.24 | 8.0 |
图 10(a)为细编穿刺C/C复合材料的结构示意图,利用周期性和对称性,取其中一个周期编织结构的1/4部分作为分析单胞(粗线框内),见图 10(b)。

|
图10 细编穿刺碳/碳复合材料结构示意图 (a)完整模型;(b)周期性部分 Fig.10 Schematic diagram of fine weave pierced C/C composites (a)whole model;(b)periodic part |
考虑到X,Y向纤维束局部微波动的角度正、负的概率是一样的,即从宏观平均上来看复合材料仍是正交各向异性的,因此在单胞中假设一半X向纤维束的波动倾角为θx,另一半为-θx,同理,Y向的纤维束也作同样的假设,以使单胞保持正交各向异性。
整体坐标系下纤维束的刚度矩阵Q′y为:
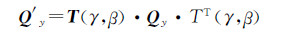
|
(5) |
式中:Qy为纤维束在局部坐标系下刚度矩阵;T为转换矩阵;γ为纤维束轴向与X轴夹角;β为纤维束在YOZ平面上的投影与Y轴的夹角,如图 11所示。

|
图11 坐标转换示意图 Fig.11 Schematic diagram of coordinate transformation |
转换矩阵T如式(6)所示。

|
(6) |
式中:l,m和n为方向角度余弦,其中l1=cosγ,l2=cosβsinγ,l3=sinγsinβ,m1=1,m2=-sinβ,m3=cosβ,n1=sinγ,n2=-cosγcosβ,n3=-sinβcosγ。
复合材料的整体刚度矩阵Qc如式(7)所示[23]。

|
(7) |
根据基体模量Em,X和Y向纤维束偏角θx,θy的分布,分别生成10组满足各自分布的随机数,通过排列组合,可以得到1000组组合,从而得出1000组复合材料等效弹性常数。计算结果发现拉伸模量和剪切模量均服从Laplace分布,泊松比服从正态分布。图 12所示为Y向的拉伸模量Ey,XY的面内剪切模量Gxy以及泊松比νxy的分布。

|
图12 细编穿刺C/C复合材料弹性常数概率分布图 (a)Ey;(b)Gxy;(c)νxy Fig.12 Probability distribution map of elastic constants of fine weave pierced composites (a)Ey;(b)Gxy;(c)νxy |
C/C复合材料考虑缺陷影响的9个弹性常数的分布类型、期望和标准差,以及不考虑缺陷的理想模型的弹性常数如表 3所示。理想模型的单向拉伸模量和泊松比均大于实际模型,模量相差幅度在5.75%~8.77%之间,泊松比相差幅度在26.1%~54.6%之间,而剪切模量两种模型互有大小,相差幅度在0.186%~8.64%之间。
| Item | Ex/GPa | Ey/GPa | Ez/GPa | νxy | νxz | νyz | Gxy/GPa | Gxz/GPa | Gyz/GPa |
| DP | Laplace | Laplace | Laplace | Normal | Normal | Normal | Laplace | Laplace | Laplace |
| EX | 30.43 | 29.66 | 22.03 | 0.1138 | 0.0970 | 0.1269 | 5.37 | 5.43 | 5.79 |
| SD | 0.0748 | 0.1467 | 0.0283 | 0.0010 | 0.0015 | 0.0026 | 0.0113 | 0.031 | 0.0565 |
| IM | 32.18 | 32.26 | 23.68 | 0.16 | 0.15 | 0.16 | 5.38 | 5.28 | 5.29 |
| ER/% | 5.75 | 8.77 | 7.49 | 43.6 | 54.6 | 26.1 | 0.186 | -2.76 | -8.64 |
| Note: DP-distribution pattern,EX-expert,SD-standard deviation,IM-ideal model,ER-error | |||||||||
实验所用试件有两种规格,长(l)×宽(b)×厚(t)=74mm×(14.8或18)mm×5mm。在WDW-100电子式万能试验机上采用三点弯曲加载,实验装置如图 13所示,共进行16组实验。

|
图13 三点弯曲实验装置 Fig.13 Three point bending testing device |
实验加载速率为0.5mm/min,实验得到中点加载处的挠度增量Δf和加载增量ΔP。弹性模量可通过公式(8)计算得出。
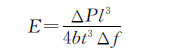
|
(8) |
计算得出试件Y方向拉伸模量的大小和分布如图 14所示,平均值为27.82GPa,比理论的平均值低6.6%,分布满足Laplace分布,尺度参数为0.86GPa。误差产生的原因可能为本模型没有考虑到复合材料中微裂纹的影响,也没有考虑到复合材料拉、压模量之间可能存在的差别,更精细的模型还应考虑到上述这些因素。

|
图14 C/C复合材料试件拉伸模量 Fig.14 Tensile modulus of C/C composite specimens |
(1)本工作提出的两步阈值筛选法可以辨别低对比图像的组分边界,适用于识别C/C复合材料CT图像中的纤维束/基体边界。
(2)对一种细编穿刺C/C复合材料显微CT图像进行统计分析,发现其基体孔隙率、X向纤维束的局部弯曲度满足正态分布,而Y向纤维束的局部弯曲度满足Laplace分布。
(3)采用上述细观结构参数建立力学模型,发现C/C复合材料拉伸和剪切模量满足Laplace分布,泊松比满足正态分布。与理想模型的结果相比,拉伸模量和泊松比均小于理想模型,模量相差幅度在 5.75%~8.77%之间,泊松比相差幅度在26.1%~54.6%之间,而剪切模量两种模型互有大小,相差幅度在0.186%~8.64%之间。
(4)采用三点弯曲实验测得的面内(Y向)模量满足Laplace分布,均值比理论预测低6.6%。误差产生的原因可能是模型没有考虑到复合材料中微裂纹的影响,复合材料拉、压模量之间可能存在的差别以及纤维/基体之间不完整的界面层的影响。
| [1] | 益小苏, 杜善义. 复合材料手册[M]. 北京: 化学工业出版社, 2009 : 639 . |
| [2] | 罗瑞盈. 碳/碳复合材料制备工艺及研究现状[J]. 兵器材料科学与工程,1998, 21 (1) : 64 –70. LUO Rui-ying. Present study situation and technology of preparation for carbon/carbon composites[J]. Ordnance Material Science and Engineering,1998, 21 (1) : 64 –70. |
| [3] | SHEEHAN J E, BUESKING K W, SULLIVAN B J. Carbon-carbon composites[J]. Annual Review of Materials Science,1994, 24 : 19 –44. |
| [4] | BLANC R, GERMAIN C, BAYLOU P, et al. Fiber orientation measurements in composite materials[J]. Composites Part A: Applied Science and Manufacturing,2006, 37 (2) : 197 –206. |
| [5] | SIRON O, LAMON J. Damage and failure mechanisms of A3-directional carbon/carbon composite under uniaxial tensile and shear loads[J]. Acta Materialia,1998, 46 (8) : 6631 –6643. |
| [6] | BLANCO C, CASAL E, GRANDA M, et al. Influence of fibre-matrix interface on the fracture behaviour of carbon-carbon composites[J]. Journal of the European Ceramic Society,2003, 23 (15) : 2857 –2866. |
| [7] | ALY-HASSAN M S, HATTA H, WAKAYAMA S, et al. Comparison of 2D and 3D carbon/carbon composites with respect to damage and fracture resistance[J]. Carbon,2003, 41 (5) : 1069 –1078. |
| [8] | HAN J C, HE X D, DU S Y. Oxidation and ablation of 3D carbon-carbon composite at up to 3000℃[J]. Carbon,1995, 33 (4) : 473 –478. |
| [9] | JACOBSON N S, CURRY D M. Oxidation microstructure studies of reinforced carbon/carbon[J]. Carbon,2006, 44 (7) : 1142 –1150. |
| [10] | 冯炎建, 冯祖德, 李思维, 等. C/SiC复合材料微结构的显微CT表征分析[J]. 航空材料学报,2011, 31 (2) : 49 –54. FENG Yan-jian, FENG Zu-de, LI Si-wei, et al. MicroCT characterization on microstructure of C/SiC composites[J]. Journal of Aeronautical Materials,2011, 31 (2) : 49 –54. |
| [11] | SOMASHEKAR A A, BICKERTON S, BHATTACHARYYA D. Compression deformation of a biaxial stitched glass fiber reinforcement: visualization and image analysis using X-ray micro-CT[J]. Composites Part A: Applied Science and Manufacturing,2011, 42 (2) : 140 –150. |
| [12] | 冯炎建, 冯祖德, 刘永胜, 等. 2D C/SiC复合材料高温蠕变损伤的显微CT分析[J]. 金属热处理,2011, 36 (Suppl) : 482 –485. FENG Yan-jian, FENG Zu-de, LIU Yong-sheng, et al. Micro-CT analysis of high temperature creep damage of 2D C/SiC composites[J]. Heat Treatment of Metals,2011, 36 (Suppl) : 482 –485. |
| [13] | MARTÍN-HERRERO J, GERMAIN C. Microstructure reconstruction of fibrous C/C composites from X-ray micro tomography[J]. Carbon,2007, 45 (6) : 1242 –1253. |
| [14] | MARTÍN-HERRERO J. Hybrid object labelling in digital images[J]. Machine Vision and Applications,2007, 18 (1) : 1 –15. |
| [15] | 阚晋. 碳/碳复合材料微细观结构的表征及对有效性能的影响研究[D]. 哈尔滨:哈尔滨工业大学, 2010. |
| [16] | 曾筝, 董芳华, 陈晓, 等. 利用MATLAB实现CT断层图像的三维重建[J]. CT理论与应用研究,2004, 13 (2) : 24 –29. ZENG Zheng, DONG Fang-hua, CHEN Xiao, et al. Three dimensions reconstruction of CT image by MATLAB[J]. CT Theory and Applications,2004, 13 (2) : 24 –29. |
| [17] | 张爱东, 李炬, 孙灵霞. MATLAB编程实现连续断层工业CT图像的三维重建[J]. 核电子学与探测技术,2006, 26 (4) : 489 –491. ZHANG Ai-dong, LI Ju, SUN Ling-xia. Three dimensional reconstruction of continuous CT images by MATLAB[J]. Nuclear Electronics & Detection Technology,2006, 26 (4) : 489 –491. |
| [18] | NIXONM S, AGUADOA S. 特征提取与图像处理[M]. 北京: 电子工业出版社, 2011 . |
| [19] | 胡更开, 郑泉水, 黄筑平. 复合材料有效弹性性质分析方法[J]. 力学进展,2001, 31 (3) : 361 –393. HU Geng-kai, ZHENG Quan-shui, HUANG Zhu-ping. Micromechanics methods for effective elastic properties of composite materials[J]. Advances in Mechanics,2001, 31 (3) : 361 –393. |
| [20] | MORI T, TANAKA K. Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metallurgica,1973, 21 (5) : 571 –574. |
| [21] | CHAMIS C C. Mechanics of composite materials-past, present and future[J]. Journal of Composites Technology and Research,1989, 11 (1) : 3 –14. |
| [22] | 袁辉. 碳/碳复合材料刚度与强度预测模型研究[D]. 南京: 南京航空航天大学, 2009. |
| [23] | 李典森, 卢子兴, 卢文书. 三维四向编织复合材料刚度和强度的理论预测[J]. 应用数学和力学,2008, 29 (2) : 149 –156. LI Dian-sen, LU Zi-xing, LU Wen-shu. Theoretical prediction of the stiffness and strength of three-dimensional and four-directional braided composites[J]. Applied Mathematics and Mechanics,2008, 29 (2) : 149 –156. |
 2016, Vol. 44
2016, Vol. 44


