文章信息
- 左平, 魏大盛, 王延荣. 2015.
- ZUO Ping, WEI Da-sheng, WANG Yan-rong. 2015.
- FGH95粉末高温合金裂纹闭合效应及裂纹扩展特性研究
- Crack Closure Behavior and Crack Propagation Characteristic of FGH95 Powder Metallurgy Superalloy
- 材料工程, 43(8): 56-61
- Journal of Materials Engineering, 43(8): 56-61.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2015.08.010
-
文章历史
- 收稿日期:2014-07-03
- 修订日期:2015-01-03
2. 先进航空发动机协同创新中心, 北京 100191
2. Co-Innovation Center for Advanced Aero-Engine, Beijing 100191, China
粉末高温合金是现代航空发动机涡轮盘的主要材料之一,具有拉伸强度高、抗疲劳性能好、可塑性高等优点。但同时也存在韧性低、对缺陷敏感、蠕变性能差等缺点。即使很小的缺陷都可能成为粉末合金结构件上裂纹的萌生点。研究粉末高温合金裂纹扩展规律,对于延长结构件的使用寿命、提高结构的安全性具有指导意义。裂纹闭合效应是影响粉末高温合金裂纹扩展规律的重要因素之一,以往针对粉末高温合金裂纹扩展规律的研究对其考虑较少,而引入裂纹闭合效应来解释粉末高温合金的裂纹扩展规律和提高裂纹扩展寿命的预测精度是很有必要的。
Elber[1]发现了裂纹闭合效应,认为裂纹闭合后裂纹表面传递的压应力对于裂纹的扩展没有贡献,即裂纹闭合后外载荷对于裂纹体将不会造成损伤。之后许多研究者对二维裂纹闭合[2, 3, 4, 5]效应进行了研究,提出了影响裂纹闭合效应的主要参数,并在此基础上对三维裂纹闭合效应[6]进行了研究。Newman等[7, 8]将裂纹闭合效应引入小裂纹计算模型中,解释了小裂纹扩展规律,并建立了小裂纹扩展寿命预测模型。过去几十年,裂纹闭合效应对裂纹扩展的影响,尤其是对小裂纹扩展的影响一直是疲劳断裂领域研究的热点之一。限于实验技术的局限性,目前国内对于裂纹闭合效应的研究大多基于数值模拟计算,缺乏实验数据支持。鉴于此,本工作基于FGH95高温合金的实验数据,分析了其CT试样裂纹面上的应力变化,探讨了影响裂纹闭合效应的主要因素,其中包括材料的本构模型,网格密度以及应力比。在此基础建立考虑闭合效应的裂纹扩展寿命预测模型,提高了裂纹扩展寿命的预测精度。
1 裂纹闭合效应的数值模拟模型 1.1 数值方法根据裂纹闭合效应的诱因,将裂纹闭合现象分为五类:塑性诱发闭合,粗糙度诱发闭合,氧化诱发闭合,相变诱发闭合和黏性流体诱发闭合。本工作主要研究塑性诱发闭合。图1为裂纹尖端塑性区的示意图。a为实际裂纹长度。前塑性区是在载荷最大时裂纹尖端附近材料屈服形成的,其半径rp可以通过式(1)进行估算。
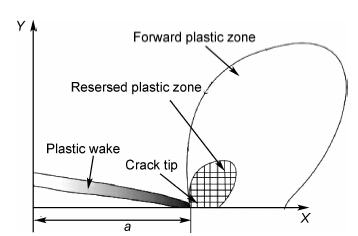 | 图1 裂纹尖端塑性区 Fig.1 Plastic zone around the crack tip | |
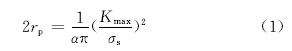
反向塑性区是裂纹尖端附近的材料在最小载荷时屈服而形成的,而塑性尾迹是裂纹扩展后残留在裂纹面上的塑性区,一般认为反向塑性区和塑性尾迹中的残余压应力是诱发裂纹闭合的根本原因,因此,模拟反向塑性区以及塑性尾迹的准确性及精度对于裂纹闭合效应至关重要。
1.1.1 裂纹扩展的数值方案裂纹扩展方式采用节点释放法,初始状态下,裂纹面上相对应的节点是粘连在一起的,在一个循环载荷周期的最小载荷处释放节点,裂纹便向前扩展一个网格单元长度,在最小载荷处释放节点有利于计算的收敛。释放节点后需经历一个完整的循环后再释放下一个节点,图2给出了节点释放的示意图。
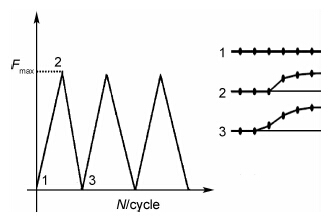 | 图2 载荷历程与节点释放示意图 Fig.2 Load history and node release scheme | |
为了避免裂纹面上的节点在裂纹闭合时发生相互渗透,需要采取一些措施来避免这种现象的发生。一般是在裂纹面相对应的节点间添加弹簧单元,弹簧单元是一个可变刚度的单元。在裂纹闭合时,弹簧单元的刚度为一个很大的值,阻止了裂纹面上节点渗透;当裂纹张开时,弹簧单元的刚度又变为零,这样就不会影响裂纹面的性质。这种方法缺点在于操作比较复杂,且计算时由于节点间弹簧单元刚度的突变,容易造成计算结果的发散。后来又发展了许多裂纹面的接触方法,如节点位移限制法[9],刚性面法[10]等,本工作采用刚性面法。
1.1.3 裂纹张开-闭合的判据合理选择裂纹张开或闭合的判据是研究裂纹闭合效应的重点之一,数值上的判据主要有节点位移法[11],节点应力法[12]等。节点位移法是通过监测裂纹尖端后节点的位移值来判断裂纹闭合与否,当裂纹面上相对应节点之间的距离小于某个值(工程上定义一个小量)时,认为裂纹闭合。这种方法的缺点是计算结果不稳定,容易出现波动。节点应力法则是通过监测裂纹尖端后的节点应力变化来判断裂纹闭合与否,当裂纹尖端后节点应力由压缩应力变为拉伸应力时认为裂纹张开,反之,则闭合,这种方法应用最为广泛,且计算结果更容易收敛。
1.2 计算模型选取FGH95粉末高温合金的CT试样作为计算模型,如图3所示,试样的厚度为10mm。
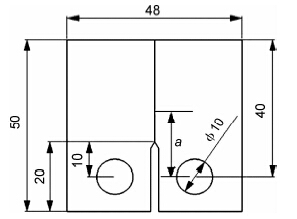 | 图3 CT试样模型 Fig.3 CT specimen model | |
考虑结构的对称性,取一半进行建模分析,有限元模型如图4(a)所示,单元为四边形平面应力单元,并对裂纹尖端进行网格局部细化,如图4(b)所示。
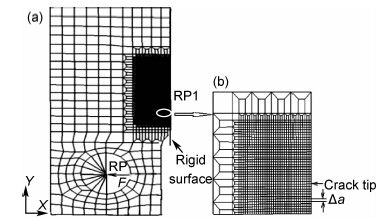 | 图4 CT试样的有限元模型 (a)整体网格模型;(b)裂纹尖端网格模型 Fig.4 Mesh model for CT specimens (a)overall model;(b)crack tip mesh model | |
FGH95粉末高温合金在430,600℃的材料属性如表1所示。选取430℃下的材料参数,载荷为三角波循环载荷,幅值为2.5kN,频率为1Hz,应力比r=0,施加在图4(a)中的参考点上(RP),边界条件施加在刚性面参考点上(RP1)。
| Temperature/℃ | Poison’s ratio | Elastic modulus/GPa | Yield strength/MPa |
| 430 | 0.185 | 182.2 | 1113 |
| 600 | 0.153 | 171.25 | 1090 |
在循环载荷作用下,由于应力集中裂纹尖端会出现局部塑性变形,卸载后仍会有残余应力。裂纹长度(静止裂纹)a为14.42mm,裂纹尖端单元尺寸为7.776μm,在最小载荷和最大载荷状态下,垂直于裂纹方向(X方向)的应力在裂纹面的变化如图5所示。
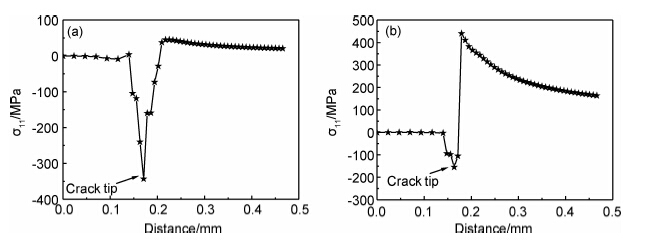 | 图5 裂纹面上沿X方向的应力分布 (a)最小载荷;(b)最大载荷 Fig.5 The stress distribution of X-direction in crack surface (a)minimum load;(b)maximum load | |
从图5(a)可以看到,在裂纹尖端附近出现了一个压应力区,即反向塑性区,越靠近裂纹尖端位置压应力越大,并在裂纹尖端处达到最大值。图5(b)中,裂纹尖端后部处于自由状态,不受约束,裂纹尖端及附近部分区域仍存在残余压缩应力,随着裂纹的扩展这一区域便会在裂纹面上形成塑性尾迹,正是由于反向塑形区以及塑形尾迹的存在,才导致了裂纹闭合效应的发生。在裂纹面上,随着离裂纹尖端距离的增加,应力逐渐降低,最后趋于稳定。
2.2 本构模型的影响选取理想弹塑性模型和多线性随动强化模型进行对比计算研究,FGH95高温合金的两种本构模型的应力-应变曲线如图6所示。
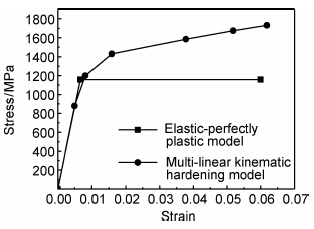 | 图6 FGH95高温合金的应力-应变曲线 Fig.6 Stress-strain curves for FGH95 superalloy | |
两种本构模型下,裂纹尖端在不同单元尺寸下的裂纹闭合效应随裂纹长度的变化关系如图7所示。横坐标表示用裂纹尖端塑性区尺寸(rp)对裂纹扩展长度(a)进行无量纲化,纵坐标表示用最大应力强度因子(Kmax)对裂纹张开应力强度因子(Kop)无量纲化。从图7可知,随裂纹扩展裂纹闭合效应趋于稳定。理想弹塑性模型下,网格尺寸对裂纹闭合效应的影响比较明显,计算结果之间比较分散。随着裂纹尖端单元尺寸减小,裂纹闭合效应逐渐降低,原因在于裂纹尖端网格单元越小,用于判断裂纹闭合的节点离裂纹尖端就越近,其相应的力学状态与裂纹尖端的差别就越小,越能反映裂纹尖端实际的力学状态。多线性随动强化模型中,网格尺寸对裂纹闭合效应的影响相对较小,计算结果比较集中,原因在于多线性强化模型更能反映FGH95材料本身的特性,所以计算结果会更精确。
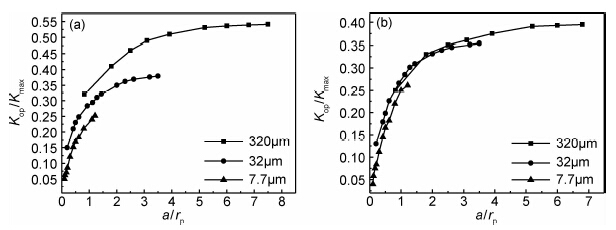 | 图7 不同本构模型下Kop/Kmax随a/rp的变化关系 (a)理想弹塑性模型;(b)多线性随动强化模型 Fig.7 Kop/Kmaxversus a/rp with different constitutive models (a)elastic-perfectly plastic model;(b)multi-linear kinematic hardening model | |
研究发现,Kop/Kmax与a/rp之间可以用函数关系式描述:
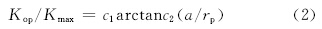
通过计算得到常数c1,c2后,便可进一步得到式(2)的渐近线为c1π/2,并用此作为裂纹闭合效应的稳定值。
使用函数关系式的意义在于:通过这种方法得到的闭合效应值比任意给定一个裂纹长度得到的裂纹闭合效应更为合理。另外,当裂纹尖端单元较小时,为了得到稳定的裂纹闭合效应值,需要经过很多次循环来实现裂纹的扩展,这需要消耗大量的计算时间,利用这个关系式可以提高计算效率。
2.3 网格密度的影响运用2.2中提出的渐近线方法研究网格密度对裂纹闭合效应的影响。引进无量纲量

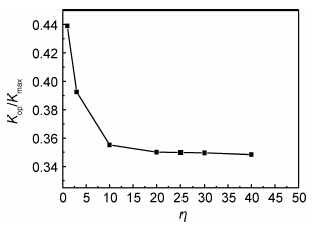 | 图8 Kop/Kmax随η变化图 Fig.8 Kop/Kmax versus η | |
从图8可知,随裂纹尖端塑性区内的网格数增加,裂纹闭合效应逐渐减小,当裂纹尖端塑性区内网格数达到20时,裂纹闭合效应趋于稳定。值得注意的是:裂纹尖端的网格密度不是越高越好,一方面,裂纹尖端网格密度越高,单元的应变畸变就越大,计算就越不容易收敛,且需要耗费很大的计算成本。另一方面,当网格尺寸小于或与晶粒尺寸相当时,有限元得到的应力应变结果可能就不能真实地反映裂纹尖端实际的应力应变状态,误差反而会越来越大。
2.4 应力比的影响在CT试样中载荷的应力比与裂纹尖端的应力比是不相同的,由于获取裂纹尖端应力比较困难,选取载荷应力比(下称应力比)作为研究对象。在裂纹闭合效应的研究中,应力比一般较小或为负值,原因在于应力比的增大会对裂纹张开/闭合的判断带来困难。图9给出了不同应力比r下Kop/Kmax随η的变化关系图。
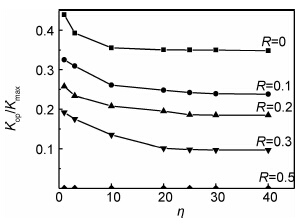 | 图9 不同应力比r下Kop/Kmax随η变化图 Fig.9 Kop/Kmax versus ηwith different stress ratio r | |
从图9可知,随应力比的增大,无量纲量Kop/Kmax逐渐减小,这说明应力比增加裂纹闭合效应逐渐减小。当r=0.5时,Kop/Kmax=0。研究表明,在最大应力不变的情况下,随着应力比的增大,σmin也不断增加,增加的σmin会抵消掉裂纹面上的部分残余压应力,使得促使裂纹闭合的残余压应力减小,即裂纹张开/闭合应力减小。当载荷谱中的最小载荷与裂纹面上的残余应力刚好抵消,即σop=σmin时,裂纹处于完全张开状态,此时就不存在裂纹闭合效应。应力比是决定裂纹闭合效应存在的关键因素之一,通过图9便可以大致估算出FGH95材料CT试样裂纹闭合效应存在的应力比范围。
但值得注意的是,上述的数值分析方法中仍存在一些不足之处,例如采用节点释放的方式虽然能够模拟裂纹扩展,但该方法没有明确的物理意义,在理论上缺乏依据;运用的本构模型不能考虑裂纹尖端的棘轮效应和应力松弛现象,完善这些不足之处将是今后工作的方向之一。
3 裂纹扩展寿命分析考虑裂纹闭合效应后,Paris公式[13]变为:
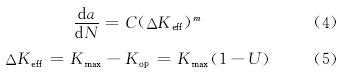

将式(5)带入式(4),得到:
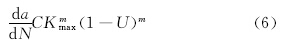
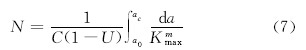
图10给出了600℃、6.5kN载荷下FGH95合金CT试样Kmax与裂纹长度a的变化关系图。
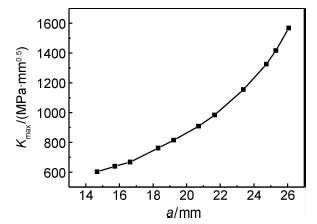 | 图10 Kmax随裂纹长度a的变化关系图 Fig.10 Kmaxversus crack length a | |
对Kmax与a的关系进行三次多项式拟合可得:
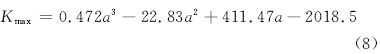
根据文献[14]中材料常数c,m分别为8.0544×10-13,2.848,选取初始裂纹长度a0为14.68mm,计算从初始裂纹度扩展到不同终止裂纹时的循环寿命(循环数)。
图11给出了裂纹扩展长度a与循环数N的关系。不考虑裂纹闭合效应寿命预测模型的预测结果偏于保守,随着裂纹长度的增加,预测寿命的误差不断增加,最大误差达到35.81%。考虑闭合效应模型得到的曲线与实验曲线更接近,预测寿命值与实验值相比略微偏大,最大误差为7.43%。计算表明,考虑裂纹闭合效应之后,预测寿命的精度提高,并可在一定条件下适当延长工程结构的使用期限,提高经济性。
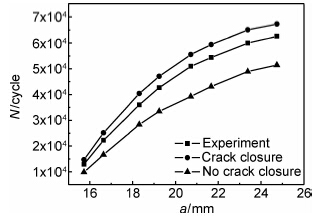 | 图11 不同寿命预测模型下的N随a的变化图 Fig.11 N versus awith different life predict models | |
(1)理想弹塑性模型下的裂纹闭合效应对网格单元的敏感性比多线性随动强化模型高,裂纹闭合效应随裂纹的扩展逐渐趋于稳定。
(2)随裂纹尖端网格密度的增加,裂纹闭合效应逐渐减小,当裂纹尖端塑性区内网格数达到20时,裂纹闭合效应趋于稳定。
(3)随着应力比r的增加裂纹闭合效应减小,研究表明,当r=0.5时,FGH95材料CT试样已经不存在裂纹闭合效应。
(4)传统的寿命预测模型偏于保守,考虑裂纹闭合效应后的寿命预测模型计算精度提高。虽然只是在FGH95材料CT试样上验证了准确性,但是这种分析过程可运用于复杂的工程结构。
| [1] | ELBER W. Fatigue crack closure under cyclic tension[J].Engineering Fracture Mechanics,1970,2(1):37-45. |
| [2] | GONZALEZ-HERRERA A,ZAPATERO J. Influence of minimum element size to determine crack closure stress by the finite element method[J].Engineering Fracture Mechanics,2004,72(3):337-355. |
| [3] | SOLANKI K, DANIEWICZS R, NEWMAN J C. Finite element analysis of plasticity-induced fatigue crack closure: an overview[J].Engineering Fracture Mechanics,2005,71(2):149-171. |
| [4] | JIANG Yan-yao,FENG Miao-lin, DING Fei. A reexamination of plasticity-induced crack closure in fatigue crack propagation[J]. International Journal of Plasticity,2004,21(9):1720-1740. |
| [5] | 陈勇,宋迎东,高德平. FGH95 粉末高温合金裂纹闭合数值模拟[J].材料科学与工程学报,2004,22(3):347-350.CHEN Yong, SONG Ying-dong, GAO De-ping.Numerical simulation of crack closure in FGH95 powder metallurgy superalloys[J]. Journal of Materials Science & Engineering,2004,22(3):347-350. |
| [6] | HOU C Y. Three-dimensional finite element analysis of fatigue crack closure behavior in surface flaws[J]. International Journal of Fatigue,2004,26(11):1225-1239. |
| [7] | NEWMAN J C, WU X R, ZHAO W, et al.Small crack growth and fatigue life prediction for high-strength aluminum alloys: part I-experimental and fracture mechanics analysis[J].Fatigue and Fracture of Engineering Materials and Structures,1998,21(11): 1289-1306. |
| [8] | NEWMAN J C, WU X R, SWAIN M H, et al. Small crack growth and fatigue life prediction for high-strength aluminum alloys: part II-crack closure and fatigue analysis[J].Fatigue and Fracture of Engineering Materials and Structures,2000,23(1):59-72. |
| [9] | SOLANKI K, DANIEWICZ S R, NEWMAN J C. A new methodology for computing crack opening values from finite element analyses[J].Engineering Fracture Mechanics,2003,71(7):1165-1175. |
| [10] | 陈亚龙,杨晓光. 带保载平面应变塑性诱发裂纹闭合效应[J].航空动力学报,2010,25(9):2030-2035. CHEN Ya-long,YANG Xiao-guang. Plasticity-induced fatigue crack closure under plane strain condition with dwelling[J].Journal of Aerospace Power,2010,25(9):2030-2035. |
| [11] | McCLUNG R C, SEHITOGLU H. On the finite element analysis of fatigue crack closure-1.basic modeling issues[J].Engineering Fracture Mechanics,1989,33(2):237-252. |
| [12] | BLANDFORD R S,DANIEWICZ S R,SKINN ER J D. Determination of the opening load for a growing crack: evaluation of experimental data reduction techniques and analytical models[J]. Fatigue Fract Eng Mater Struct,2002,25(1):17-26. |
| [13] | PARIS P C, ERDOGAN F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering Transaction of the ASME,1963,85:528-534. |
| [14] | 魏大盛,王延荣.粉末冶金涡轮盘裂纹扩展特性分析[J].推进技术,2008,12(6):753-758. WEI Da-sheng,WANG Yan-rong. Lifing methodology of crack propagation in powder metallurgy turbine disk[J].Journal of Propulsion Technology,2008,12(6):753-758. |




