文章信息
- 江冯, 李萍, 程从前, 刘春慧, 赵杰. 2015.
- JIANG Feng, LI Ping, CHENG Cong-qian, LIU Chun-hui, ZHAO Jie. 2015.
- θ投影法和复合模型在预测耐热钢蠕变行为的比较分析
- Comparative Analysis of Creep Behavior Prediction of Heat Resistant Steel Based on Theta Projection and Composite Model
- 材料工程, 43(7): 87-92
- Journal of Materials Engineering, 43(7): 87-92.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2015.07.015
-
文章历史
- 收稿日期:2014-03-21
- 修订日期:2014-12-08
随着经济的快速发展和对电能需求日益增加,许多高参数大容量的超(超)临界机组投入使用。然而在高温高压下长期服役的高温构件会发生蠕变变形使得构件失效的概率增加,因而精确预测寿命和持久强度对高温炉管的使用年限和设计极其重要。高温持久寿命和蠕变是评价高温强度的重要性能指标,传统寿命预测和强度设计的方法是TTP参数法[1, 2, 3],但TTP参数外推法中参数值与应力之间不是线性关系,因而在运用高应力外推低应力的时候不能外推太久,否则预测曲线会偏离实际持久性能,从而造成在工程应用中的危险[4],因蠕变与高温持久寿命之间的密切关系,一些研究者提出结合短时蠕变实验结果预测长时的持久性能,如θ投影法[5],Omega法[6],Graham-Walles法[7]等。这些方法一般是通过拟合实验所得的蠕变曲线得到蠕变曲线方程,从而能够预测各温度和应力下蠕变曲线,然后结合断裂应变可以实现持久寿命的预测,因此近年来受到研究者普遍关注,并将这些方法运用在许多耐热钢中[8, 9]。与此同时,一些报道也指出在利用这些方法预测时仍然可能出现较大的预测误差,而是否能够准确描述蠕变行为是关系预测精度的关键。Oikawa等[10]在预测铁素体耐热钢蠕变寿命时,对θ投影法进行相应的修正并运用修正后的θ投影法对CrMoV和12Cr(H46)等钢的蠕变寿命进行了预测,其精度可达到90%。Sandstrom[11]指出在预测蠕变寿命时应运用多种描述蠕变曲线的方法进而提高预测精度,并分别运用θ投影法描述蠕变第一阶段和Omega法描述蠕变第三阶段。然而在已有报道中,相当部分主要以预测方程是否与蠕变实验曲线吻合为判定准则,而对于人们更为关注的外推效果评述不够。
本工作运用θ投影法和θ投影法结合Graham-Walles法的复合模型评价P92钢的蠕变性能。运用两种蠕变模型进行了外推P92钢的最小蠕变速率与应力曲线的比较分析并在不同蠕变应变下也比较分析了两者外推最小蠕变速率与断裂时间的曲线。同时考察不同蠕变应变对寿命预测的影响,结合蠕变信息和蠕变模型对比分析了预测持久寿命的精度。
1 实验材料及分析方法选定P92钢作为实验材料,其成分符合ASME A335标准,温度为600℃,应力为200,205,215,225,235MPa和温度在650℃,应力为125,135,150,165,175MPa进行蠕变实验,并采用以下两种蠕变参数法拟合并对比分析蠕变行为。
θ投影法:把蠕变过程看成由蠕变第1阶段的硬化过程和蠕变第3阶段的软化过程所组成,整个蠕变曲线的表达式为:
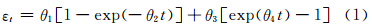
复合模型:Graham-Walles法描述蠕变第一阶段和θ投影法描述蠕变第三阶段,其表达式为:
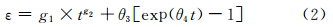
式(1)和(2)中,ε是t时的蠕变变形量,θ和g是与应力和温度有关的参数且满足以下关系:
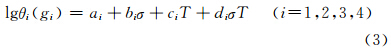
式中,ai,bi,ci和di为材料常数,通过非线性最小二乘法拟合式(3)中的参数值,从而可知任意温度和应力下的θ和g值,结合式(1)和(2)则可计算相应的蠕变曲线。
基于上述方程得到最小蠕变速率:对关系式(1)的时间t求二次导数,导数为0时对应的时间为蠕变达到最小蠕变速率的时间tm,如式(4)所示,将式(4)所得tm带入式(5)得到的蠕变速率即为最小蠕变速率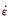 m。
m。
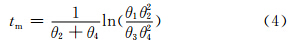
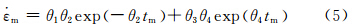
同理对表达式(2)对时间t求二次导数,当导数为0时对应的时间即为最小蠕变速率对应的时间tm,即式(6)中的tm。通过式(7)可以求得最小蠕变速率。
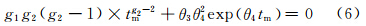
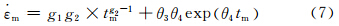
为得到θ投影法和复合模型外推最小蠕变速率与时间的关系,结合所得的θ参数和式(1)即知到达一定蠕变应变时的时间,从而外推最小蠕变速率与时间的曲线。同理结合所得的g参数和式(2)即知到达一定蠕变应变时的时间,从而外推最小蠕变速率与时间的曲线。通过运用蠕变模型外推蠕变速率与应力和时间的关系,本工作旨在运用不同蠕变模型描述蠕变行为之间进行对比分析。同时在不同的断裂应变时,进行外推持久性能比较分析。
2 结果与讨论 2.1 蠕变曲线的描述及蠕变曲线预测的比较分析基于蠕变模型外推蠕变曲线与蠕变速率曲线,并将两者与实验数据点进行对比,分析两种模型外推的差异。图1(a)是650℃不同应力下运用模型外推的蠕变曲线,图1(b)是运用模型外推的蠕变速率曲线。
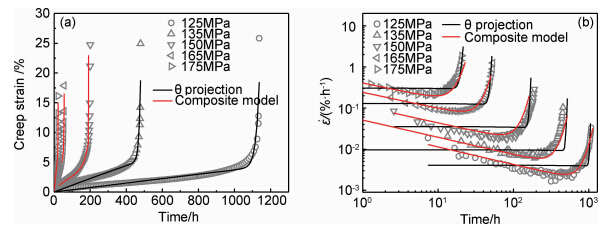 | 图1 蠕变模型拟合的曲线与实验数据的对比 (a)蠕变曲线;(b)蠕变速率曲线 Fig.1 Comparison of creep model directly fit curves and experimental data (a)creep curves;(b)creep rate curves | |
从图1(a)可知运用θ投影法和复合模型直接拟合蠕变曲线时,拟合曲线与实验数据吻合,拟合精度均在0.90205到0.99984之间。表明两种模型的预测方程能表征P92钢的应变与时间曲线。图1(b)是拟合参数关联温度和应力后运用两种模型外推的蠕变速率与时间的关系曲线,从图1(b)可知θ投影法能较好的描述蠕变曲线第三阶段,但θ投影法外推的蠕变速率曲线在第一阶段与P92真实蠕变速率曲线有较大差异。有报道指出[12]在许多材料中蠕变第一阶段是整个塑性变形的重要组成部分,从图1中也可知P92钢的蠕变曲线基本上是由第一阶段和第三阶段组成,第一阶段占整个蠕变断裂时间的比例较大。如果蠕变第一阶段不能正确描述可能会对长时间的蠕变曲线外推和寿命预测精度有影响。然而复合模型却能精确地描述P92钢蠕变曲线的第一阶段和第三阶段,因复合模型的预测方程在描述蠕变第一阶段时,其蠕变速率与时间在双对数坐标下呈线性关系,与P92钢的蠕变速率随时间的变化规律一致。而θ投影法能很好地描述蠕变第三阶段,所以复合模型运用θ投影法来描述第三阶段并结合Graham-Walles法描述第一阶段来预测P92钢的蠕变行为就较θ投影法更能精确地描述P92钢的蠕变特性。
2.2 蠕变模型预测蠕变速率的比较分析
两种模型预测的最小蠕变速率与实测值的相对大小能验证两种模型的预测精度[13],运用式(5)和式(7)可预测两种模型的P92钢最小蠕变速率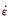 min,并与实验所得最小蠕变数据
min,并与实验所得最小蠕变数据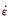 exp进行对比分析,如图2所示。
exp进行对比分析,如图2所示。
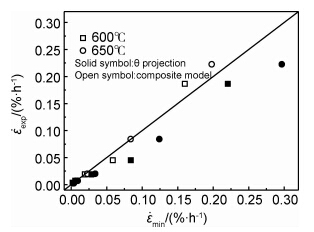 | 图2 基于θ投影法和复合模型预测最小蠕变速率与实测值的对比分析 Fig.2 Comparison of extrapolated minimum creep rates with experimental value based on θ projection and composite model | |
图2可知θ投影法预测值与实测值之间偏差较大,通过预测值与实测值的差值分析,θ投影法的预测值与实测值相对误差的最大值达到了86.2%。而复合模型的预测值与实测值均较好的分布在Y=X的直线上,复合模型的预测值与实测值相对误差的最大值为30.2%,表明预测值与实测值的符合性较好。出现这种现象的原因可能是θ投影法不能较好地描述P92钢的蠕变第一阶段,因而预测精度也较复合模型稍差。从图1(b)中两种模型预测的蠕变速率曲线也能表征两者最小蠕变速率的差异。
在一定的温度下,一个受单向拉伸应力的试样的蠕变应变ε随时间而增加的规律与温度、应力、时间及组织状态有关[14],以双曲正弦函数模型为基准,比较分析两种不同模型外推最小蠕变速率与应力,如图3所示。
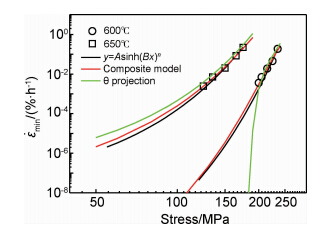 | 图3 基于θ投影法和复合模型外推应力与最小蠕变速率的对比分析 Fig.3 Comparison of extrapolated minimum creep rates with stress based on θ projection and composite model | |
图3中两种模型在预测最小蠕变速率与应力曲线的同时也运用适用型更广的双曲正弦函数的预测结果来验证两种模型的精度。图3所示在数据点范围内,实测值均能在θ投影法和复合模型的预测曲线上。但在外推至低应力时,在650℃,两种模型的预测曲线与双曲正弦函数模型外推的趋势一致,呈现出外推的合理性。然而在600℃时,θ投影法外推曲线在190MPa处发生偏折呈现出预测的不合理性,然而复合模型的外推曲线与实际蠕变特征相符。蠕变曲线记录并反映了蠕变机理作用的过程而蠕变模型在描述蠕变曲线时依存于模型表达式,模型中的参数值与温度和应力的关系是否拟合良好是外推的关键所在。复合模型能较θ投影法更好的描述P92钢的蠕变行为,这也说明了复合模型的数学表达式能很好地表征蠕变的每个阶段从而预测的精度会较高。
设定不同的蠕变断裂应变,基于两种模型外推最小蠕变速率与时间曲线,如图4所示。
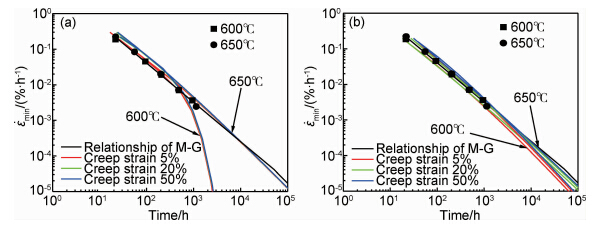 | 图4 不同应变时外推最小蠕变速率与时间曲线 (a)θ投影法;(b)复合模型 Fig.4 The extrapolation of minimum creep rate and time curves at various strain (a)θ projection;(b)composite model | |
图4所示在实验数据点的范围内,最小蠕变速率与时间在双对数坐标中呈现出良好的线性关系,符合Monkman-Grant[15]关系。其表达式如下:

在数据点范围内,两种模型预测的曲线均较吻合数据点。外推时,两种模型在650℃预测的曲线呈良好的线性关系并与M-G关系外推趋势一致。但在600℃外推时,θ投影法的预测曲线出现偏折与M-G线性的关系不符,预测趋势呈现出不合理性,而复合模型在600℃时预测曲线与M-G线性的关系相符,预测趋势呈现出合理性。
同时基于实验数据点能得到的M-G方程并外推10万小时曲线作为标准,来评判不同模型在不同温度下的预测精度。本工作中以应变量20%为例进行比较,两模型的外推与时间的关系如图5所示。
 | 图5 两模型预测最小蠕变速率的相对误差与时间的关系 Fig.5 The relationship of time and standard error of min creep rate at various rupture strain based on θ projection and composite model | |
从图5可知θ投影法在长时预测的最小蠕变速率值与M-G关系曲线之间的相对误差随着时间的增加而越来越大,10万小时达到100%,然而复合模型预测的相对误差在整个最小蠕变速率外推的过程中最大为66.2%,比θ投影法的预测误差相对来说小得多。出现偏差较大的原因是θ投影法以θ参数反映温度和应力对蠕变各阶段的作用,在θ参数值关联温度与应力后进行蠕变曲线描述时,θ投影法的描述就依存于方程表达式,因不能较好地描述P92蠕变应变-时间曲线和蠕变速率-时间曲线而致使较大的相对误差产生。同样,复合模型能较好的描述P92钢的蠕变性能,使得预测精度较θ投影法更高。上述表明描述P92钢的蠕变模型不仅要分析在实验数据范围内的拟合程度,还要关注外推后预测结果的合理性和可靠性。
2.3 蠕变模型预测持久寿命的比较分析运用θ投影法和复合模型进行持久寿命的预测并比较分析,在模型表达式中的参数值均关联温度和应力,拟合后的参数值带入式(1)和式(2),通过设定一定的断裂应变即可进行寿命预测。图6给出了蠕变应变与温度和应力的关系。从图中可知不同温度与应力下的断裂应变均很好的分布在三者变量的外推三维曲面上,断裂应变在1%~50%的范围内。
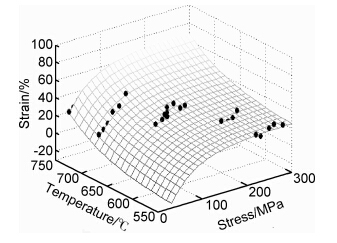 | 图6 断裂应变与温度和应力之间的关系 Fig.6 Relationship between breaking strain and temperature or stress | |
通过图6的结果分别设定蠕变应变为1%,5%,50%进行持久断裂寿命的预测。图7给出了两种模型在不同蠕变应变时外推的持久性能曲线与P92钢持久断裂数据[16]和ASEM公布的Gr92钢的持久数据[17]进行对比。
图7所示在650℃时,ASME Gr92数据均匀分布在断裂应变为1%至50%预测的持久曲线之间,然而在600℃时,在实验值范围内复合模型比θ投影法的预测寿命曲线能稍好的包含ASME Gr92数据,但外推长时寿命曲线时两者均偏离数据点并呈偏高的趋势。大体而言两种模型的预测寿命有差距,但差距不大。可能是因为模型运用关联温度与应力的参数值后评估蠕变行为出现了偏折现象,在运用此模型表达式来预测时精度就相对稍差。在600℃两种模型均预测偏高的原因不排除实验钢的批次等因素,实际P92钢的持久数据是不同批次实验所得,因此在利用蠕变参数法不能仅从单一批次的持久数据来预测,而应该运用不同批次的持久断裂数据预测并应充分考虑材料性能的波动性和分散性来提高预测精度。同时图7中也可知应变5%~50%之间外推的曲线几乎重合,这说明了蠕变应变为5%~50%时,对蠕变行为的预测影响不大。大范围波动的蠕变应变寿命预测相差不大的原因是蠕变应变大约在5%后,进入快速的第三阶段,此时应变增加非常快,伸长率的变化只能引起相当小的寿命的变化。
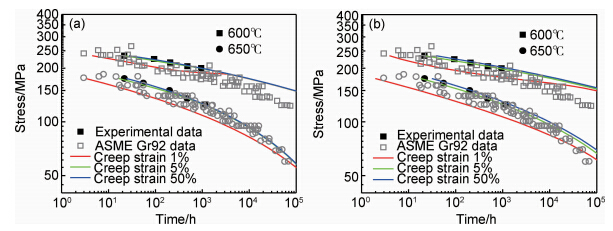 | 图7 不同蠕变应变下,预测持久性能曲线与实验值和ASMEGr92数据对比分析 (a) θ投影法;(b)复合模型 Fig.7 Comparison of predicted rupture line with experimental data and ASME Gr92 data based on θ method (a) and composite model (b) at different creep strain | |
(1)直接拟合蠕变曲线时,θ投影法和复合模型均能得到很好的拟合效果,但在关联蠕变速率与时间关系时,复合模型能很好地描述蠕变第一阶段的减速和第三阶段的加速特征,而θ投影法在描述蠕变第一阶段时偏差较大,不能准确描述P92钢的蠕变行为。
(2)利用两种方法外推蠕变速率结果表明:在实验数据点内,预测结果与实验数据符合良好。但外推时,θ投影法在600℃预测的最小蠕变速率与应力和断裂时间曲线均出现了偏离,而复合模型在不同温度下呈现出很好的线性预测趋势。而且蠕变应变的大小对描述蠕变行为影响不大。
(3)利用两种方法外推持久寿命结果表明:蠕变应变的大小对通过蠕变数据来预测持久寿命预测影响不大,而且在蠕变应变为5%~50%时,寿命预测结果之间相差不大。θ投影法和复合模型两者相比,在预测持久寿命上差距小。
| [1] | LARSON F R, MILLER J.A time-temperature relationship for rupture and creep stress [J]. ASME Trans, 1952, 74(5):765-771. |
| [2] | ORR R L, SHERBY O D, DORN J E. Correlation of rupture data for metals at elevated temperatures[J]. ASME Trans,1954,76(1):113-128. |
| [3] | 刘春慧,程从前,赵杰,等. MHZ常数在耐热钢持久性能预测中的应用[J].材料工程,2012, (10):12-16. LIU C H,CHENG C Q,ZHAO J, et al. Prediction of creep rupture property using MHZ constant for heat resistant steel[J]. Journal of Materials Engineering, 2012, (10):12-16. |
| [4] | 张俊善.材料强度学[M]. 哈尔滨:哈尔滨工业大学出版社,2004. ZHANG J S.Strength of Materials[M]. Harbin:Harbin Institute of Technology Press, 2004. |
| [5] | KIM W G, YIN S N, KIM Y W, et al. Creep characterization of a Ni-based Hastelloy-X alloy by using theta projection method [J]. Engineering Fracture Mechanics, 2008,75 (17): 4985-4995. |
| [6] | 孙海生,徐彤,关凯书. Omega 蠕变寿命评估方法及应用[J]. 压力容器, 2012, 29(9): 19-23. SUN H S, XU T, GUAN K S. Description and application of omega creep life assessment[J].Pressure Vessel Technology,2012,29(9):19-23. |
| [7] | GRAHAM A, WALLES K F A. Relationships between long and short-time creep and tensile properties of a commercial alloy[J].Journal of the Iron and Steel Institute of Japan, 1955, 179(12): 105-120. |
| [8] | 杨王玥,李志文. θ法预测 12Cr1MoV 钢主蒸汽管道材料剩余寿命[J]. 金属学报,1999,35(7) :721-725. YANG W Y, LI Z W. The residual life evaluation for main steam pipe of 12Cr1MoV steel in power plant by the θ projection concept[J].Acta Metallurgica Sinica,1999,35(7):721-725. |
| [9] | LBARRA S,KONET R R. Life assessment of 11/4 Cr-1/2 Mo steel catalytic reformer furnace tubes using the MPC omega method[J]. Journal of Pressure Vessel Technology,1995,117(19):19-23. |
| [10] | OIKAWA H,MARUYAMA K. Prediction of long-term creep curves [J]. Fusion Engineering and Design,1992,19(4) : 321-328. |
| [11] | SANDSTROM R. Basic model for primary and secondary creep in copper [J]. Acta Materialia, 2012, 60(1):314-322. |
| [12] | ESPOSITO L, BONORA N. Primary creep modeling based on the dependence of the activation energy on the internal stress [J]. Journal of Pressure Vessel Technology-Transactions of the ASME,2012,134(6):061401-1. |
| [13] | CHEN G L, GUO H, SUN J Y, et al. Extrapolation model of high temperature creep for 12CrMoV steel [J]. Pressure Vessel Technology,2011,28(8):11-15. |
| [14] | 黄硕,万敏,黄霖,等.铝合金蠕变试验及本构模型建立[J].航空材料学报,2008,28(1):93-96. HUANG S,WAN M, HUANG L, et al. Aluminum alloy creep test and its constitutive modeling [J].Journal of Aeronautical Materials,2008,28(1):93-96. |
| [15] | RAY A K, DIWAKAR K, PRASAD B N, et al. Long term creep-rupture behavior of 813K exposed 2.25-1Mo steel between 773 and 873K[J]. Materials Science and Engineering A,2007,454-455(25):124-131. |
| [16] | 刘春慧. 超(超)临界用钢高温持久寿命外推方法的比较分析[D]. 大连:大连理工大学,2013. LIU C H. Comparative analyses of life prediction methods for steels used in (ultra)super critical units [D].Dalian: Dalian University of Technology, 2013. |
| [17] | KIMURA K, SAWADA K, KUBO K, et al. Influence of stress on degradation and life prediction of high strength ferritic steels [A].ASME Pressure Vessel and Piping Division Conference Proceedings[C].USA: ASME, 2004. 11-18. |
 2015, Vol. 43
2015, Vol. 43


