文章信息
- 童第华, 吴学仁, 刘建中, 胡本润, 陈勃. 2015.
- TONG Di-hua, WU Xue-ren, LIU Jian-zhong, HU Ben-run, CHEN Bo. 2015.
- 基于小裂纹理论的铸造钛合金ZTC4疲劳寿命预测
- Fatigue Life Prediction of Cast Titanium Alloy ZTC4 Based on the Small Crack Theory
- 材料工程, 43(6): 60-65
- Journal of Materials Engineering, 43(6): 60-65.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2015.06.010
-
文章历史
- 收稿日期:2014-07-10
- 修订日期:2014-11-20
ZTC4作为一种优质的铸造钛合金具有良好的抗蚀性、高的强度重量比、优良的疲劳抗力以及断裂韧性,在飞机机身结构和航空发动机上都得到了广泛的应用,吸引了研究者的关注[1]。航空工程结构中,疲劳断裂问题是无法忽视的重要问题。铸造件中不可避免地存在着夹杂、疏松、气孔等初始缺陷,容易成为构件疲劳破坏的源头。为保证ZTC4及同类铸造构件确定服役期限及保证服役期间使用安全等需求,需要对ZTC4的疲劳寿命做出预测。因此本文对ZTC4铸件进行了不同应力比的疲劳实验,利用扫描电镜对试样断口和疲劳源位置的分析观察,发现试样的裂纹源大多都位于边缘部位的夹杂、疏松等初始缺陷处。以初始缺陷尺寸为寿命起点,采用基于小裂纹理论的疲劳全寿命预测方法[2, 3, 4, 5, 6, 7, 8, 9, 10],利用Fastran II软件[5]对ZTC4的疲劳寿命进行了预测。
1 实验过程及方法 1.1 静力性能ZTC4铸造钛合金的化学成分见表1。采用如图1所示的试样进行静力性能测试,所有试样均从材料的纵向取样,实验方法按HB5143—1996[11]执行,其静力拉伸性能见表2。
| Al | V | Fe | C | N | O | H | Si | Ti |
| 6.06 | 4.12 | 0.12 | 0.004 | 0.01 | 0.112 | 0.0026 | 0.05 | Bal |
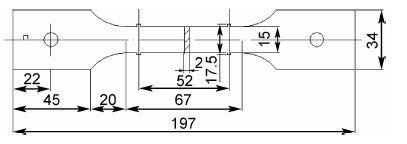 | 图1室温静力性能试样 Fig.1 Room temperature tensile property test specimen | |
| Material | σb/MPa | σ0.2/MPa | δ5/% | E/GPa |
| ZTC4 | 834 | 737 | 6.1 | 114 |
将ZTC4铸造钛合金加工成图2所示的疲劳板材试样,应力集中系数Kt=1。分别进行应力比R=0.06和R =-1的疲劳S-N 曲线测试,实验方法按HB5287—1996[12]执行。
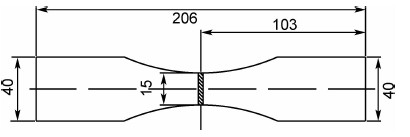 | 图2 疲劳试样( Kt=1) Fig.2 Fatigue specimen(Kt=1) | |
采用成组法测试了两个应力比的S-N 曲线(见图3),每条曲线采用三级应力水平,每级应力水平15个试样,并采用升降法测试107循环寿命对应的中值疲劳极限,疲劳极限测试12~15个试样,共测试了120个试样。
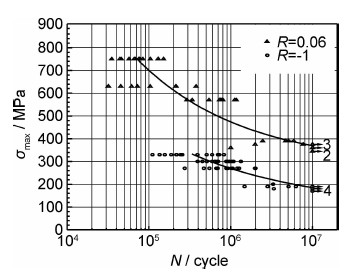 | 图3 两种应力比的ZTC4疲劳S-N曲线 Fig.3 Fatigue S-Ncurves of ZTC4 at two stress ratios | |
观察图2所示的试样疲劳断口发现,95%以上的疲劳裂纹起始和扩展都位于试样中部截面的边缘处附近 (见图4)。裂纹主要萌生于铸造引起的夹杂处,其尺寸在20~70μm之间,距表面的深度在50~800μm之间(见图5)。在裂纹扩展区观察到疲劳辉纹,能看到清晰的疲劳条带,且存在少量的二次裂纹。由夹杂引起的疲劳断裂试样个数占53%,由疏松、缩孔和微裂纹等引起的约占47%。
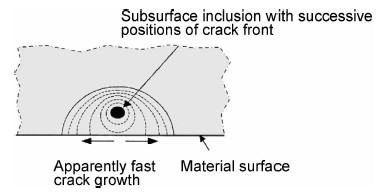 | 图4 疲劳裂纹萌生及扩展示意图 Fig.4 Schematic diagram of fatigue crack initiation and propagation | |
 | 图5 ZTC4夹杂疲劳源SEM图像(a)试样1;(b)试样2;(c)试样3 Fig.5 SEM images of ZTC4 fatigue origins caused by inclusions (a)specimen 1;(b)specimen 2;(c)specimen 3 | |
对试样断口扫描电镜分析发现,16%的疲劳断裂是由疏松引起的(见图6),裂纹源主要萌生于铸造引起的疏松处,并形成一种光学暗区(Optically Dark Area,ODA),距表面500~1000μm; 裂纹扩展区可以观察到清晰的疲劳条带和明显的二次裂纹。
除夹杂与疏松作为裂纹源外,还有部分疲劳断裂是由缩孔和微裂纹引起的(见图7),裂纹源距表面的深度在200~1200μm之间。裂纹扩展区可以观察到清晰的轮胎花纹(疲劳辉纹),疲劳断口由疲劳裂纹源区、疲劳裂纹扩展区以及瞬断区三部分组成。裂纹在试样自由表面或靠近表面的地方形成,近裂纹源处裂纹呈放射状;其后随着裂纹的扩展,裂纹逐渐稀疏,扩展速率加快;瞬断区的断口形貌跟静载断裂相似,形成不平坦的粗糙表面。
 | 图6 ZTC4疏松疲劳源SEM图像(a)试样4;(b)试样5 Fig.6 SEM images of ZTC4 fatigue origins caused by porosities(a)specimen 4;(b)specimen 5 | |
 | 图7 ZTC4缩孔、微裂纹疲劳源SEM图像 Fig.7 SEM images of ZTC4 fatigue origins caused by shrinkage cavities and microcracks (a)specimen 6;(b)specimen 7 | |
根据扫描电镜分析结果和统计分析,铸造夹杂、疏松、缩孔等缺陷的众数约为50μm,距离厚度表面的众数为700μm(见图8和图9)。因此在后面的预测模型中将初始缺陷的尺寸假设为50μm,深度为700μm。
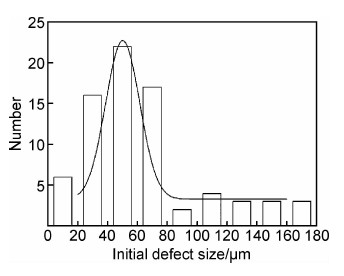 | 图8 ZTC4初始缺陷尺寸统计分布 Fig.8 Statistical distribution of ZTC4 initial defect size | |
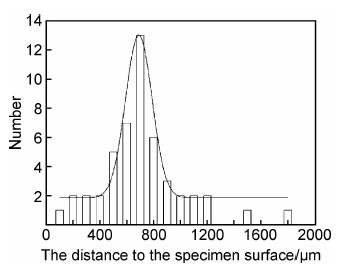 | 图9 ZTC4初始缺陷深度统计分布 Fig.9 The statistical distribution of ZTC4 initial defect depth | |
在ZTC4试样的断口分析中,发现有一部分初始缺陷形式如Crack A(见图10) (图中a 和b 分别对应椭圆的长、短半轴)。也有一部分初始缺陷形式如Crack B所示,横轴不平行于试样的厚度表面,这种缺陷几何在工程实际构件中也是大量存在的,对Crack B采用等效简化计算方式(见图11)。由图11可见,其中 a ,b ,α 的定义见图10。

图10对应的应力强度因子求解是十分复杂的,目前较通用的方法是利用有限元分析求解,但是有限元方法耗时,计算效率较低。本文应用Isida和Noguchi[13]的应力强度因子解来进行分析。
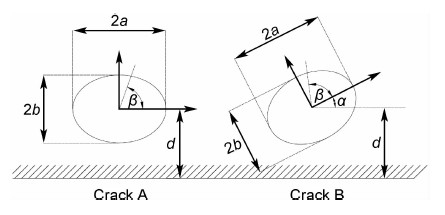 | 图10 裂纹几何 Fig.10 Crack geometry | |
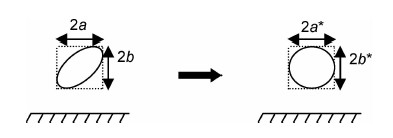 | 图11 Crack B的等效简化计算 Fig.11 The equivalent simplified calculation of crack B | |
简化后椭圆裂纹的长短轴端的应力强度因子计算公式见式(1):
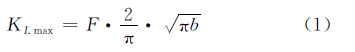
式中:F 为形状函数,最大应力强度因子发生在短轴的下端点[13],即靠近表面处,将其形状系数记为FB ,而在长轴端的系数记为FA 。
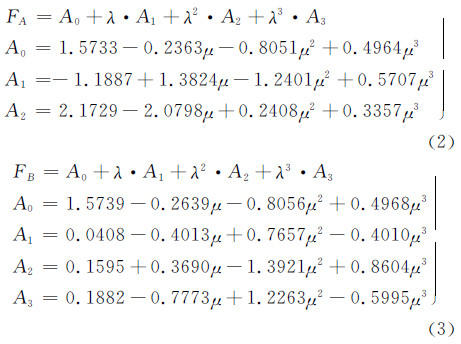
式中: d 的定义见图10。
d 的定义见图10。
采用基于小裂纹理论的疲劳全寿命预测方法[2],利用Fastran II软件[5]和Isida、Noguchi的应力强度因子解[13, 14]对ZTC4铸造钛合金的疲劳寿命进行预测。该预测方法是根据恒幅载荷下的长裂纹扩展实验数据,基于裂纹闭合模型获得裂纹扩展速率da/dN 与 有效应力强度因子ΔKeff间的关联,长裂纹的(da/dN )-ΔKeff裂纹扩展速率曲线为基础,假设在第一个载荷循环时裂纹就开始扩展,预测从初始裂纹(缺陷)尺寸直至断裂的疲劳寿命。
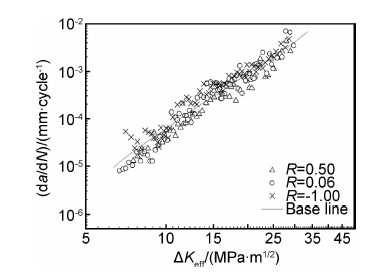
为了获得长裂纹扩展基线,实验中采用中心裂纹拉伸试样(CCT试样),试样形式见图12所示 (厚度为4mm),分别进行了R =0.5,0.06和-1的长裂纹扩展实验,扩展速率数据见图13。利用Newman裂纹张开应力公式[15](式(4))进行(da/dN )-ΔK eff裂纹扩展速率关联(见图14)。
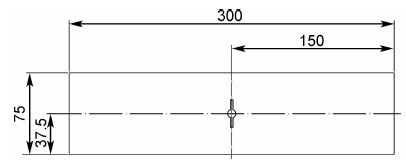 | 图12 室温裂纹扩展试样形式 Fig.12 The specimen for room temperature crack growth test | |
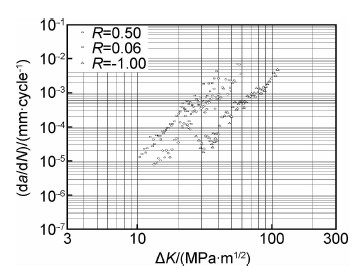 | 图13 ZTC4疲劳裂纹扩展速率(da/dN)-ΔK数据 Fig.13 Fatigue crack growth rate (da/dN)-ΔK for ZTC4 | |
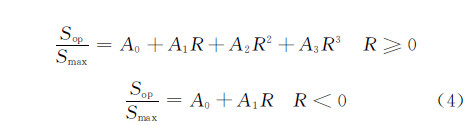
式中:Smax为最大应力;R =Smin/Smax为应力比;Sop为裂纹张开应力;A0 ,A1,A2 ,A3是应力状态约束系数α和Smax的函数,由下式给出:
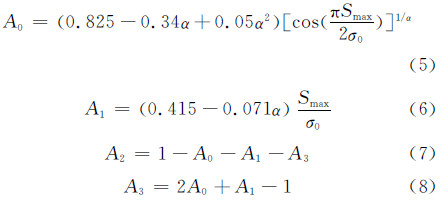
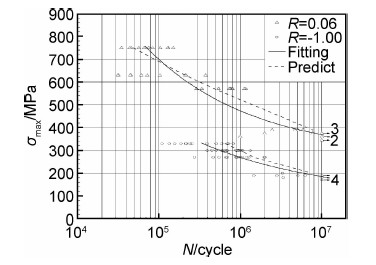
 | 图14 ZTC4疲劳裂纹扩展速率(da/dN)-ΔKeff基线 Fig.14 Fatigue crack growth rate (da/dN)-ΔKeffbase line for ZTC4 | |
从试样的宏观断裂位置看,疲劳破坏多发生在靠近试样中心截面的边缘处附近。微观分析发现,裂纹源大多萌生于夹杂、疏松等铸造引起的缺陷处。根据扫描电镜分析结果和统计分析,铸造夹杂、缩孔等缺陷的众数尺寸a=b= 50μm,距离厚度表面的众数深度d 为700μm。因此在预测模型中将初始缺陷的尺寸a 和b 假设为50μm,深度d 为700μm。采用图14中(da /dN )-ΔKeff裂纹扩展速率曲线对ZTC4铸造钛合金试样(见图2)进行疲劳寿命预测,预测结果与实验结果的比较分析见图15。由图15可见采用基于小裂纹理论的条带屈服裂纹闭合模型进行疲劳寿命预测,其结果与实验结果吻合较好。
 | 图15 S-N实验曲线和寿命预测结果的比较 Fig.15 Comparison of S-N curves and life prediction results | |
从寿命预测结果看,采用基于小裂纹理论得到的预测结果与实验结果吻合较好。这也表明以气孔、夹杂等微观缺陷的尺寸作为初始裂纹的长度,即把材料中的微观缺陷当做一个已经存在的微裂纹是比较合理的。在利用小裂纹理论和Fastran预测疲劳寿命时,初始缺陷尺寸和深度对疲劳寿命存在一定影响。下面从ZTC4疲劳试样的断口统计分析中,选取一定的特征初始尺寸和深度值,来定量分析其对疲劳寿命的影响程度[16]。
4.2 初始缺陷离表面距离的影响Fastran II在进行疲劳寿命计算时,初始缺陷离表面的距离对最终的结果会产生一定影响。文献[14]指出,对于图10的 Crack A,当 d/b 较小时,初始缺陷对应的应力强度因子值可以按照表面裂纹的应力强度因子值进行计算;当d/b 较大时,则可以按照内埋椭圆裂纹的应力强度因子值进行计算。本文计算了R =0.06,Smax=630MPa,a =b =50,75μm和100μm时,d 取不同特征深度对寿命预测值的影响,结果见图16。
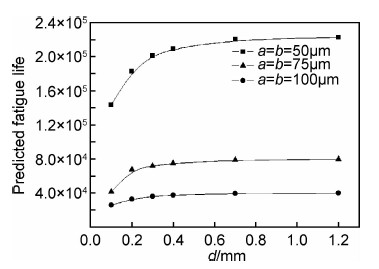 | 图16 初始缺陷位置对预测的ZTC4疲劳寿命的影响 Fig.16 nfluence of initial defect location on predicted fatigue life of ZTC4 | |
由图16可见在给定初始缺陷尺寸的情况下,当d/b 较大时,试件寿命趋于某稳定值,几乎不受d 变化影响;而在靠近表面附近时,深度d 减小会明显增大应力强度因子,使试件寿命变短。此预测结果表明,缺陷越靠近表面越会显著降低疲劳寿命。
4.3 初始缺陷尺寸的影响在基于小裂纹理论的疲劳全寿命预测中,把材料初始缺陷尺寸设定为寿命预测的起点,即初始裂纹长度。由于疲劳寿命主要消耗在裂纹尺寸很小的阶段,因此初始裂纹长度对疲劳寿命具有显著影响。本工作针对ZTC4疲劳试样(见图2),分析了ZTC4铸件中的初始缺陷尺寸对寿命预测值的影响,结果见图17。该图表明,在给定初始缺陷位置的条件下,预测的疲劳寿命随着初始缺陷尺寸的增加急剧降低。
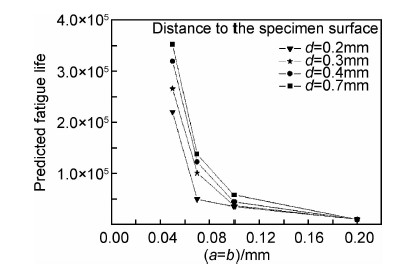 | 图17 初始缺陷尺寸对预测的ZTC4疲劳寿命的影响 Fig.17 Influence of initial defect size on predicted fatigue life of ZTC4 | |
(1)ZTC4 铸造钛合金的疲劳裂纹大多萌生于气孔、夹杂等铸造缺陷处。众数缺陷尺寸为50μm,距离厚度表面的众数深度为700μm。试样疲劳断裂是由试样本身存在的铸造缺陷引起的,绝大部分的试样断裂机制呈现多源性疲劳断裂的特征。
(2)基于小裂纹理论,采用修正的条带屈服裂纹闭合模型,预测得到的ZTC4疲劳寿命与实验结果吻合较好。在给定初始缺陷尺寸的情况下,预测的ZTC4疲劳寿命随着初始缺陷位置距离表面深度的增加而增加。在给定初始缺陷位置的条件下,预测的疲劳寿命随着初始缺陷尺寸的增加急剧降低。
| [1] | NAN H, XIE C M, ZHAO J Q. Development and application of titanium alloy casting technology in China[J]. China Foundry, 2005, 2(4): 239-245. |
| [2] | NEWMAN Jr J C. A crack-closure model for predicting fatigue crack growth under aircraft spectrum loading [J]. ASTM STP, 1981, 748:53-84. |
| [3] | ZIEGLER B, YAMADA Y, NEWMAN Jr J C. Application of a strip-yield model to predict crack growth under variable-amplitude and spectrum loading-Part 2: Middle-crack-tension specimens [J]. Engineering Fracture Mechanics, 2011, 78(14): 2609-2619. |
| [4] | LIU J Z, WU X R. Study on fatigue crack closure behavior for various cracked geometries [J]. Engineering Fracture Mechanics, 1997, 57(5): 475-491. |
| [5] | NEWMAN Jr J C. FASTRAN-2: A fatigue crack growth structural analysis program [J]. NASA STI/Recon Technical Report N, 1992, 92, 30964. |
| [6] | NEWMAN Jr J C, BROT A, MATIAS C. Crack-growth calculations in 7075-T7351 aluminum alloy under various load spectra using an improved crack-closure model [J]. Engineering Fracture Mechanics, 2004, 71(16-17): 2347-2363. |
| [7] | NEWMAN Jr J C, PHILLIPS E P, SWAIN M. Fatigue-life prediction methodology using small-crack theory [J]. International Journal of Fatigue, 1999, 21(2): 109-119. |
| [8] | 吴学仁, 刘建中. 基于小裂纹理论的航空材料疲劳全寿命预测 [J]. 航空学报, 2006, 27(2): 32-41.WU X R, LIU J Z. Total fatigue life prediction for aeronautical materials by using small-crack theory[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(2): 219-226. |
| [9] | 胡本润, 陈勃, 王利发, 等. 氩弧焊接接头疲劳寿命预测 [J]. 航空材料学报, 2005, 25(3): 28-31.HU B R, CHEN B, WANG L F, et al. Fatigue life prediction in argon-arc welded joint[J]. Journal of Aeronautical Materials,2005, 25(3): 28-31. |
| [10] | 丁传富, 刘建中, 吴学仁. TC4 钛合金和 7475 铝合金的长裂纹和小裂纹扩展特性的研究 [J]. 航空材料学报, 2005, 25(6): 11-17. DING Chuan-fu, LIU Jian-zhong, WU Xue-ren. An investigation of small-crack and long-crack propagation behavior in titanium alloy TC4 and aluminum alloy 7475-T7351. Journal of Aeronautical Materials, 2005, 25(6): 11-17. |
| [11] | HB5143-1996, 金属室温拉伸实验方法 [S]. HB5143-1996, Metal materials tensile test at room temperature [S]. |
| [12] | HB5287-1996, 金属材料轴向加载疲劳实验方法 [S]. HB5287-1996, Metal materials axial loading fatigue test method [S]. |
| [13] | ISIDA M, NOGUCHI H. Tension of a plate containing an embedded elliptical crack [J]. Engineering Fracture Mechanics, 1984, 20(3): 387-408. |
| [14] | NOGUCHI H, SMITH R, CARRUTHERS J, et al. Stress intensity factors of embedded elliptical cracks and an assessment of the ASME XI defect recharacterisation criteria [J]. International Journal of Pressure Vessels and Piping, 1997, 70(1): 69-76. |
| [15] | NEWMAN Jr J C. A crack opening stress equation for fatigue crack growth [J]. International Journal of Fracture, 1984, 24(4): 131-135. |
| [16] | 陈勃, 刘建中, 吴学仁, 等. 初始缺陷尺寸分布的尺寸效应研究 [J]. 航空学报, 2006, 27(1): 44-49. CHEN Bo,LIU Jian-zhong,WU Xue-ren,et al. Study of size effect on initial flaw size distribution[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(1): 44-49. |
 2015, Vol. 43
2015, Vol. 43


