文章信息
- 张勇, 谢卫红, 刘宏伟, 张峰. 2015.
- ZHANG Yong, XIE Wei-hong, LIU Hong-wei, ZHANG Feng. 2015.
- 聚氨酯蜂窝纸板动力学性能及其本构模型
- Dynamic Mechanical Properties and Constitutive Model of Honeycomb Paperboard Filled with Polyurethane
- 材料工程, 43(5): 27-32
- Journal of Materials Engineering, 43(5): 27-32.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2015.05.005
-
文章历史
- 收稿日期:2013-10-18
- 修订日期:2014-11-25
2. 空军勤务学院 机场工程与保障系, 江苏 徐州 221000
2. Department of Airport Engineering and Safeguard, Air Force Service College, Xuzhou 221000, Jiangsu, China
在现代战争和抗灾抢险中,空投运输发挥出越来越重要的作用,它日益成为一种重要的物资补给手段[1]。为有效降低空投物资着陆时的冲击加速度,需要在空投载荷着陆时采取着陆缓冲或是减振抗冲击措施,吸收空投物资下降的动能。目前,泡沫材料和蜂窝结构是应用最广的两种防护型包装材料。对蜂窝纸板的研究工作主要集中在影响蜂窝纸板静、动态力学性能的一些参数,蜂窝结构隔热、隔音、吸震性能[2]和对温、湿度的敏感性[3, 4],蜂窝结构的力学模型[5, 6]、蜂窝芯的平面压缩数值模拟等[7, 8]。聚氨酯蜂窝纸板复合材料兼有两者的优点,能提升蜂窝材料动态缓冲性能。因此,聚氨酯蜂窝纸板的研究对空投物资的缓冲吸能防护具有重要意义。
在蜂窝纸板本构模型方面,主要研究了蜂窝纸板静态荷载和冲击荷载下压缩过程中各个阶段的力学本构方程,以及等效弹性模量计算模型、非线性黏弹塑性模型以及不同应变率下的变形模式[9, 10, 11]等。在泡沫塑料的本构模型方面,主要研究了考虑大变形、温度效应和应变率效应的泡沫材料的压缩模型[12, 13, 14]。将聚氨酯填充到蜂窝纸板中,聚氨酯泡沫这一增强相的加入改善了蜂窝纸板的力学性能,同时也使其本构关系变得更为复杂。目前为止,文献中针对聚氨酯蜂窝纸板的动态弹塑性本构关系模型的研究很少,只能参考聚氨酯或蜂窝纸板的一些本构方程。
本工作利用改造的马歇特落锤进行冲击实验,测试了聚氨酯蜂窝纸板的动态力学性能,并对这一新型复合材料的动力学本构模型进行研究。
1 动态冲击实验 1.1 实验材料聚氨酯泡沫采用上海沪泾建材有限公司生产的单组分聚氨酯泡沫填缝剂(简称OCF)获得。将聚氨酯填缝剂瓶罐倒置并均匀晃动约1min,然后打开喷嘴将均匀发泡的聚氨酯泡沫冲入自制的模具,待其固化后拆模,并根据实验所需切割成厚度为20,15mm和10mm的单纯聚氨酯试件。
蜂窝纸板选用了三种规格:孔径6mm、厚度15mm;孔径8mm、厚度20mm;孔径10mm、厚度20mm。将刚发泡的半固体状的聚氨酯泡沫用喷头均匀喷涂在蜂窝纸芯表面,这时要从纸质蜂窝芯的喷涂聚氨酯泡沫一面进行加压,使得聚氨酯泡沫能够通过纸质蜂窝芯并从另一端溢出(如图 1所示)。
 |
图 1 复合材料制作步骤图 Fig.1 Fabrication of composite material |
空投缓冲系统的冲击仍属于低速低载荷的冲击,因此选择重锤实验作为研究新型聚氨酯蜂窝纸板复合材料的实验方法。在东南大学力学实验中心研发的马歇特落锤实验设备(图 2)基础之上,改装成具备测试与数据采集分析功能、符合聚氨酯蜂窝纸板复合材料特点的一套冲击实验设备。
 |
图 2 落锤冲击实验系统 Fig.2 Drop test arrangement |
信号测试系统包括信号测量和数据分析两个模块。信号测量模块包括冲击位移传感器和应变式力传感器,在冲击过程中,安装在两侧支架上的挠度式位移计或安装在下夹板孔内的竖直位移计记录位移时程曲线,所受冲击力由位于下夹板下的应变式力传感器记录,完成整个冲击过程。数据分析系统主要包括计算机和基于LabVIEW的四通道采集分析程序,LabVIEW程序实现了对位移和力信号的同步采集(图 3)。该套落锤冲击实验设备能够独立完成冲击过程和数据采集分析过程,选定力信号和位移信号具有相同时间起点,实测得到的力信号和位移信号真实有效可信,信噪比符合控制范围。经过上述过程,就可以得到每一次冲击过程的载荷-位移曲线。经过进一步计算,可以获得反映新型聚氨酯蜂窝纸板材料的动应力-动应变特征曲线。
 |
图 3 数据传感与测量系统 Fig.3 Data sensing and measurement system |
一般要求当空投装备物资到达地面时,其着地速率为3~6m/s,大约相当于从0.5~1.8m处跌落[15],这为选择合适的冲击速率进行实验提供了依据。为了真实模拟这一工况,最终采用的冲击速率为5m/s,这相当于从1.25m高度处自由下落到达地面时的速率。
假设空投时缓冲衬垫面积为4m×2.5m,空投质量为1000~8000kg,则触地面积均布载荷为100~800kg/m2,即要求落锤均布质量为100~800kg/m2。假设动态力学实验所用试件标准面积为5cm×5cm,那么其对应质量范围应该为0.25~2kg。这样,选择重锤质量为2kg,对应的实际状况为在1m2的面积上空投800kg装备。以上重锤质量和高度设置基本符合中轻型空投乃至重型空投的实际工况,在此基础上,进一步进行了试件方案的设计。
实验共分A,B,C,D四组进行研究。为消除偶然误差,每组的每种试件均制作3个,冲击后得到的数据取平均值。
本文仅列出A组的试件参数,A组实验方案将复合材料中的蜂窝纸芯孔径作为变量进行研究,试件孔径大小遵循单变量法则,即在其他因素相同的条件下改变试件内蜂窝纸芯骨架的孔径大小,共有3种,具体试件编号和参数情况如表 1所示。
| Test label | Core diameter of honeycomb paperboard/cm | Thickness of honeycomb paperboard/cm | Dropping height/m | Impact velocity/ (m·s-1) | Buffering dimension/cm |
| A1 | 0.6 | 1.5 | 1.25 | 5 | 5cm×5cm |
| A2 | 0.8 | 1.5 | 1.25 | 5 | 5cm×5cm |
| A3 | 1.0 | 1.5 | 1.25 | 5 | 5cm×5cm |
为了考察孔径变量对复合材料动态缓冲性能的影响,现固定其他因素只改变孔径进行考察:试件编号为A1,A2和A3,A1为孔径6mm、厚度15mm的复合材料,A2为孔径8mm、厚度15mm的复合材料,A3为孔径10mm、厚度15mm的复合材料。这组的缓冲性能曲线比较见图 4(a)。
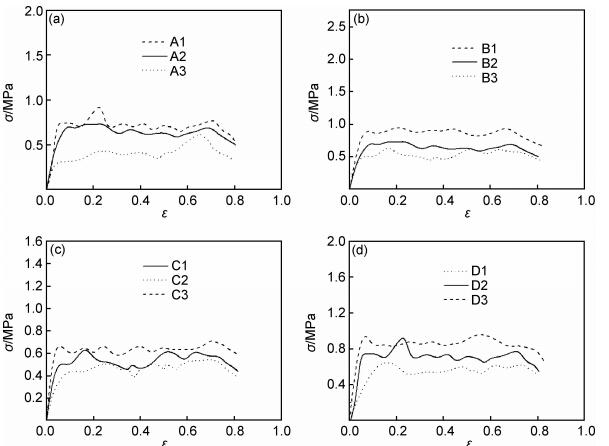 |
图 4 复合材料动态缓冲性能的四种影响因素分析 (a)孔径;(b)厚度;(c)横截面积;(d)冲击速率 Fig.4 Analyses of four kinds of influencing factors of composite material dynamic buffering performance (a)core diameter;(b)thickness;(c)buffering area;(d)impact velocity |
随着蜂窝纸芯的孔径增大,复合材料的屈服强度和弹性极限都有所下降,动应力-动应变曲线幅值减小,但屈服阶段对应的应变区间基本不变。
2.2 复合材料厚度对其动态缓冲性能影响B1,B2和B3是其他参数相同厚度不同的三种试件,其孔径都为8mm。其中B1的试件厚度为10mm,B2的试件厚度为15mm,B3的试件厚度为20mm。这组的缓冲性能曲线比较见图 4(b)。
在同样冲击速率(应变率相同)的情况下,随着复合材料厚度的逐渐增大,它的动态屈服强度和动态弹性极限会随之下降,同时动应力-动应变曲线的幅度逐渐减小,但各个阶段对应的动应变区间基本不变。
2.3 复合材料横截面积对其动态缓冲性能影响C1,C2和C3试件为只有横截面积不同而其他参数相同的三种试件,其中C1的横截面规格为5cm×5cm,C2的横截面规格为7cm×7cm,C3的横截面规格为3cm×3cm。这组的缓冲性能曲线比较见图 4(c)。
在一定范围内,随着横截面积的增大,其动态屈服强度和动态弹性极限都有所下降,动应力-应变曲线的幅度逐渐减小,但屈服阶段对应的动应变区间基本不变。
2.4 冲击速率对复合材料动态缓冲性能影响实验过程主要通过落锤坠落高度的不同来控制冲击速率的大小,共设置三个高度梯度,分别为1.00,1.25m和1.50m,通过计算可以得到对应的速率梯度为4.47,5.00m/s和5.48m/s。挑选试件编号为D1,D2和D3,它们都是孔径6mm、厚度15mm、面积为5cm×5cm的复合材料。D1对应高度为1.00m,速率为4.47m/s,D2对应高度为1.25m,速率为5.00m/s,D3对应的高度为1.50m,速率为5.48m/s。这组的缓冲性能曲线比较见图 4(d)。
在有限的范围内,随着冲击速率的逐渐增大,其动态屈服强度和动态弹性极限会随之提高,同时动应力-动应变曲线的幅度逐渐升高,但弹性阶段、屈服阶段和压实阶段所对应的动应变区间基本不变。
3 复合材料动态压缩本构模型文献[12]在建立聚氨酯泡沫本构关系时将环境温度和相对密度及应变率等因素考虑进去,提出了经验型本构关系:
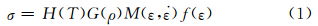
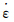 基本上无关;而M(ε,
基本上无关;而M(ε,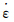 )则主要反映了应变率对应力的影响,形状函数f(ε)定义为在某一参考相对密度、参考温度、准静态加载下的应力、应变的曲线函数,它能很好地模拟材料变形的全过程。本构关系(1)考察了三种温度(-20,20,60℃)下的应力-应变曲线,将温度的影响函数H(T)定义为双折直线形式。关于相对密度对应力的影响函数则简单定义为线性形式。
)则主要反映了应变率对应力的影响,形状函数f(ε)定义为在某一参考相对密度、参考温度、准静态加载下的应力、应变的曲线函数,它能很好地模拟材料变形的全过程。本构关系(1)考察了三种温度(-20,20,60℃)下的应力-应变曲线,将温度的影响函数H(T)定义为双折直线形式。关于相对密度对应力的影响函数则简单定义为线性形式。胡时胜等[13]对本构关系(1)进行了修正,在修正的本构关系中不包含温度,并且通过实验研究发现,应变和密度两者是耦合在一起影响着应力。关于应变率对应力的影响则采用基于热激活机制的Seeger模型,得到拟合的本构关系(2):
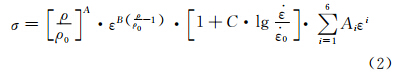
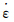 0为选定的一种参考应变率;C为拟合参数。
0为选定的一种参考应变率;C为拟合参数。基于聚氨酯蜂窝纸板复合材料的动态压缩实验数据,对本构关系(1)引入了孔径大小的影响因素,然后基于实验数据用数值方法拟合了聚氨酯蜂窝纸板复合材料应变率、应变以及孔径大小的动态压缩本构关系。
根据落锤冲击实验可知,速率变化范围很小(从4.47~5.48m/s),基本上可以认为冲击速率与应变率成正比关系,即
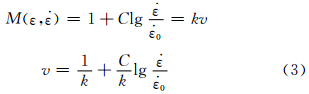
这样,就将本构关系(1)中的应变率变量转变为了速率变量。
形状函数选用多项式形式来对其加以描述,即
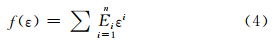
根据上述实验结论,结合本构关系(1),现提出包含蜂窝纸芯孔径大小、应变、应变率参数的具有简单形式的本构方程:
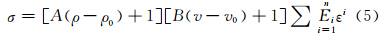
应用已经取得的实验数据对本构关系进行数据拟合,为了提高拟合精确度,使得拟合效果更好,选择n=6进行本构方程的拟合。
选取A1试件作参考,令v0=5,ρ0=6,并利用试件A1(其数据参见表 1)的应力-应变曲线进行多项式拟合,即由孔径6mm复合材料为基准拟合本构关系。经6次方拟合,得到相关参数见表 2,f(ε)数据拟合求解图如图 5所示。
| Parameter | B1 | B2 | B3 | B4 | B5 | B6 |
| Value | 18.02738 | -137.04274 | 502.2908 | -970.73262 | 948.88175 | -368.44678 |
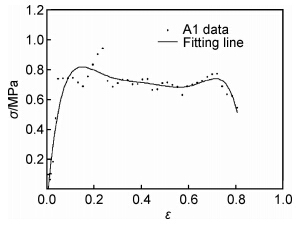 |
图 5 形状函数的数据拟合曲线 Fig.5 Data fitting curve of shape function |
因此,拟合得到的形状函数为:
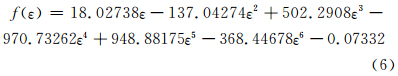
本次拟合的残差图见图 6,残差表征了变量与拟合曲线纵坐标之间符合所拟合函数之间的关系显著程度。由图 6可知,所得曲线的拟合效果较好。
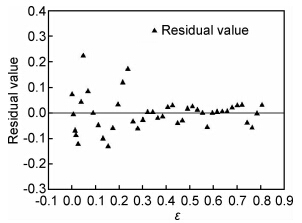 |
图 6 形状函数拟合后的残差检验图 Fig.6 Residual checkout of shape function fitting |
利用得到的形状函数,进行系数A和B的求解工作。
选取A4试件的实验数据进行拟合,可知v=v0=5,ρ=8,即由孔径8mm的复合材料进行基准拟合其本构关系。经过拟合,得到A的值为-0.1。
同样,选取D1的实验数据进行拟合,可知v=4.47,ρ=6,即由孔径8mm的复合材料进行基准拟合其本构关系。经过拟合,得到B的值为0.698。
这样,本构关系式中的参数确定,同时对参数适当省略小数并添加一个屈服后期指数修正项[16],最终得到:
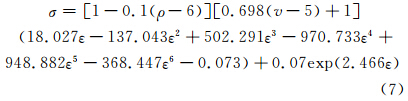
通过推导出的本构关系对其余试件进行应用,并与实验测得的应力-应变曲线进行对比,达到本构模型验证的目的。
通过图 7拟合可以发现,复合材料的动态本构关系模型对于试件的拟合有一定的效果,曲线的大部分数值能够与实测值对应,尤其是在孔径变量对动态力学性能的影响这一方面吻合较理想。普遍来看,本构方程拟合得到的曲线对于复合材料弹性阶段拟合得较好,对于失稳阶段(复合材料表现通常不明显)的拟合稍有不足。对于屈服阶段的拟合在屈服强度上相差并不太大,在达到压实段后,拟合结果不错。另外,本构方程对于各个试件对应的各应变区间把握得非常好,基本保持了与试件各阶段对应应变区间的同步化。
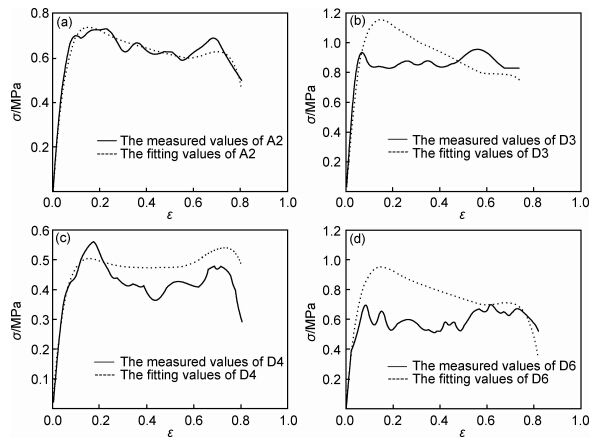 |
图 7 四种影响因素的本构模型曲线与实验数据曲线对比 (a)孔径;(b)冲击速率;(c)横截面积;(d)厚度 Fig.7 Constitutive model vs experiment data curves under four kinds of influencing factors (a)core diameter;(b)impact velocity;(c)buffering area;(d)thickness |
(1)复合材料的动态屈服强度和动态弹性极限随着蜂窝纸芯的孔径、复合材料厚度和横截面积的增大而减小,随着冲击速率的增大而提高,同时动应力-动应变曲线的弹性阶段、屈服阶段和压实阶段所对应的动应变区间基本不变。
(2)本构方程拟合得到的曲线对于复合材料弹性阶段拟合较好,对于失稳阶段(复合材料表现得通常不明显)的拟合稍有不足。同时,本构方程拟合曲线和实验曲线对应的各应变区间基本保持不变。
| [1] | 于成果,李良春. 空投安全着陆的实现途径[J]. 包装工程,2007, 28(10):135-137.YU Cheng-guo, LI Liang-chun. Ways of air-drop safety landing[J]. Packaging Engineering, 2007, 28(10):135-137. |
| [2] | WANG Zhi-wei, E Yu-ping. Energy-absorbing properties of paper honeycombs under low and intermediate strain rates[J]. Packaging Technology and Science, 2012, 25(3):173-185. |
| [3] | WANG Zhi-wei, E Yu-ping. Mathematical modelling of energy absorption property for paper honeycomb in various ambient humidities[J]. Materials & Design, 2010, 31(9):4321-4328. |
| [4] | E Yu-ping, WANG Zhi-wei. Effect of relative humidity on energy absorption properties of honeycomb paperboards[J]. Packaging Technology and Science, 2010, 23(8):471-483. |
| [5] | WANG Dong-mei, WANG Zhi-wei. Experimental investigation into the cushioning properties of honeycomb paperboard[J]. Packaging Technology and Science, 2010, 21(6):309-316. |
| [6] | WANG Dong-mei, WANG Zhi-wei, LIAO Qiang-hua. Energy absorption diagrams of paper honeycomb sandwich structures[J]. Packaging Technology and Science, 2009, 22(2):63-67. |
| [7] | WANG Liang, SUN Ling. Application of double-vaccum-bag process to the splicing technology for honeycomb sandwich structure[J]. Journal of Wuhan University of Technology, 2009, 31(21):52-55. |
| [8] | HIROAKI N, TADAHARU A, WAKAKO A. In-plane impact behavior of honeycomb structures randomly filled with rigid inclusions[J]. International Journal of Impact Engineering, 2009, 36(1):73-80. |
| [9] | CHEN D H, OZAKI S. Analysis of in-plane elastic modulus for a hexagonal honeycomb core:effect of core height and proposed analytical method[J]. Composite Structures, 2009, 88(1):17-25. |
| [10] | RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs-a finite element study[J]. International Journal of Impact Engineering, 2003, 28(2):161-182. |
| [11] | ZHENG Z J, YU J L, LI J R. Dynamic crushing of 2D cellular structure:a finite element study[J]. International Journal of Impact Engineering, 2005, 32(1-4):650-664. |
| [12] | SHERWOOD J A, FROST C C. Constitutive modeling and simulation of energy absorbing polyurethane foam[J]. Polymer Engineering and Science, 1992, 32(16):1138-1146. |
| [13] | 胡时胜,刘剑飞,王悟.硬质聚氨酯泡沫塑料本构关系的研究[J]. 力学学报,1998, 30(2):151-156. HU Shi-sheng, LIU Jian-fei, WANG Wu. Study of the constitutive relationship of rigid polyurethane foam[J]. Acta Mechanica Sinica, 1998, 30(2):151-156. |
| [14] | 卢子兴. 聚氨酯泡沫塑料拉伸本构关系及其失效机理的研究[J]. 航空学报, 2002, 23(2):151-154. LU Zi-xing. Investigation into the tensile constitutive relation and failure mechanism of pur foamed plastics[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(2):151-154. |
| [15] | 谭军,韩旭,刘鑫. 某特种车空投着陆过程数值仿真分析与改进[J]. 包装工程,2010,31(1):57-61. TAN Jun, HAN Xu, LIU Xin. Numerical analysis and improvement of airdrop landing process of special vehicles[J]. Packaging Engineering, 2010,31(1):57-61. |
| [16] | 林玉亮,卢芳云,王晓燕,等. 低密度聚氨酯泡沫压缩行为试验研究[J]. 高压物理学报,2006,20(1):88-92. LIN Yu-liang, LU Fang-yun, WANG Xiao-yan, et al. Experimental study of the compressible behavior of low-density polyurethane foam[J]. Chinese Journal of High Pressure Physics, 2006, 20(1):88-92. |
 2015, Vol. 43
2015, Vol. 43


