文章信息
- 石晓朋, 李曙林, 常飞, 卞栋梁, 尹俊杰. 2015.
- SHI Xiao-peng, LI Shu-lin, CHANG Fei, BIAN Dong-liang, YIN Jun-jie. 2015.
- 复合材料加筋壁板低速冲击响应与冲击能量关系
- Connection of Low-velocity Impact Response and Impact Energy of Stiffened Composite Panel
- 材料工程, 43(4): 53-58
- Journal of Materials Engineering, 43(4): 53-58.
- http://dx.doi.org/10.11868/j.issn.1001-4381.2015.04.010
-
文章历史
- 收稿日期:2013-12-14
- 修订日期:2014-09-11
复合材料加筋壁板结构是由加强筋(筋条)和被支撑的壳体(蒙皮)组成的结构,其不仅具有已有复合材料层合板结构比强度高、比刚度高以及结构可设计性好等特点,而且还具有自身所固有的诸多优点,例如自动化的低成本制造过程和高可靠性等[1],因而,越来越多地应用于航空航天领域和各种工程结构中。然而,复合材料加筋壁板同复合材料层合板一样,对冲击载荷十分敏感,在低速冲击载荷作用下,会出现基体开裂、分层、纤维断裂等损伤,这种损伤范围较大且不易发现,往往会给材料带来更大威胁。因此,对加筋壁板在低速冲击载荷作用下响应的研究具有重要意义。
目前,国内外许多学者针对复合材料层合板低速冲击损伤机理进行了研究。Davies等[2]用较低能量进行冲击,发现接触力与时间关系曲线近似为正弦曲线,揭示了层压板损伤面积与冲击能量、最大接触力的关系; Schoeppner等[3]总结出了分层门槛力与其他参数的相关关系;Feraboli等[4, 5, 6]证实,当冲击能量较低、且在弹性冲击阶段时,损伤萌生接触力、峰值接触力与能量成正比关系,当能量增大到能够产生损伤时,损伤会耗散能量,接触力不再增加,出现一个平台,甚至损伤一开始便出现平台,没有线性上升。
复合材料冲击损伤机理较为复杂,目前暂无精确解析解。有限元的分析作为一种高效和低成本的分析方法,能较好预测冲击响应及损伤。Lopes等[7]使用ABAQUS对冲击过程进行有限元模拟,对实验方法和数值方法的冲击力曲线以及有限元预测的损伤面积与实验的分层面积进行了比较,对能量的损伤耗散作了讨论;Wang等[8]根据Hashin准则,及损伤演化规律,实现材料随损伤出现刚度矩阵的折减;王一飞等[9]研究不同铺层层合板低速冲击响应与损伤参数之间的关系;王仁鹏等[10]基于Hashin失效准则,通过引入损伤变量对材料的弹性参数进行折减,研究了层压板在静痕作用下的损伤阻抗。古兴瑾等[11]对复合材料加筋壁板高速冲击损伤进行了数值模拟,并探讨了筋条参数对高速冲击损伤的影响规律。严实等[12]运用AE参数很好地描述了不同编织工艺参数三维编织复合材料的低速冲击过程。
本工作结合有限元仿真方法,对复合材料加筋壁板在低速冲击载荷作用下的接触力、损伤散逸能和板吸收的能量等冲击响应与冲击能量关系进行了研究,并对比了仿真与实验得到的损伤扩展结果。
1 低速冲击损伤理论分析 1.1 冲击分析模型及接触力计算最大的接触力及位移是利用能量平衡方程得到,基本假设是最大接触力或最大位移时刻所有冲击能量都变换到板中,能量损失及材料阻尼及振动略去,即
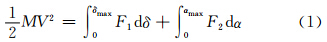
式中:M,V分别为冲击物的质量及速度;δ,α分别表示板上冲击点处的挠度及接触时的刻痕(凹坑)深度;F为接触力。方程中右边第一项为板弯曲变形能,第二项为接触表面的接触能量。

式中:k为板接触点处的刚度。显然,它是板尺寸大小、边界条件、层压板材料、板形状等的参数。用有限元分析计算时都需考虑到这些因素。
根据Hertz接触定律[13]

式中:n为Hertz接触刚度,近似用式(4),(5)求得。

或
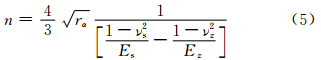
式中:Ez为板垂直板面方向的弹性模量;rα为刻痕半径;Es,νs为冲头的弹性模量及泊松比;νz为层合板的泊松比(可取ν12)。将式(2)和式(3)带入式(1)积分计算后得
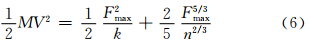
Hashin失效准则可以较好地应用于复合材料的损伤破坏分析中,本工作采用Hashin失效准则[14]作为失效判据,表达式如下
纤维断裂(σ11≥0)
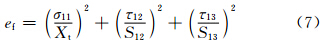
纤维屈曲(σ11<0)

基体压缩失效(σ22+σ33<0)
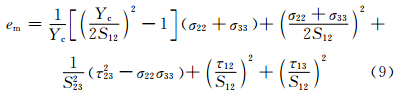
基体拉伸失效(σ22+σ33≥0)
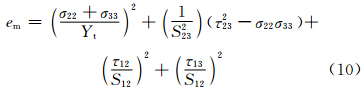
拉伸分层失效(σ33≥0)
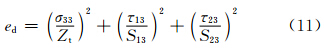
剪切分层失效(σ33<0)
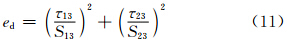
式中:1为纤维方向;2为纤维横向方向;3为厚度方向;σ为对应方向的应力;S是对应方向的剪切强度;Xt是纤维方向的拉伸强度;Yt是横向拉伸强度;Xc是纵向压缩强度;Yc是横向压缩强度;ef,em,ed分别为纤维失效因子,基体失效因子,分层失效因子,当ei≥1(i=f,m,d)时,材料失效。
1.3 刚度退化方案目前,针对复合材料损伤的刚度退化方案大致分为应力更新刚度退化方案,参数折减刚度退化方案和渐进损伤刚度退化方案。复合材料损伤过程中,损伤区域的应力分布变化很剧烈,渐进损伤刚度退化方案能较好地表征材料损伤形式和程度[17],因此,其更适合用作复合材料损伤演化的判据[18]。
在冲击过程中,当满足Hashin失效准则时,材料开始失效,刚度矩阵开始退化。纤维损伤参数df和基体损伤参数dm分别表示为[19]
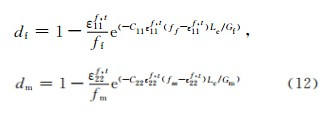
式中Lc为材料积分点处的特征长度;Gm为剪切模量。
在渐进损伤过程中,刚度矩阵根据纤维损伤参数df和基体损伤参数dm进行衰减,刚度退化方案为
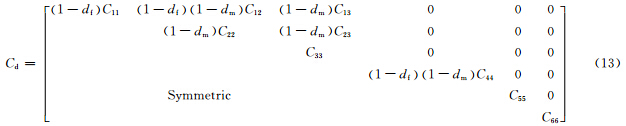
模型中加入了刚度退化方案,但是由于刚度的大幅度折减易引起计算收敛难,在显式分析中往往表现为大变形下单元的过度扭曲而导致分析进程的中止,为了提高收敛度,本工作引入基于黏滞规律的技术[16],黏滞变量为
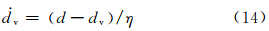
式中:η为黏滞系数;d为计算得到的纤维损伤参数或基体损伤参数;dv黏滞变量。黏滞系数的选择取决于对结果精度的要求,当黏滞系数选取较大时,其会明显延缓材料的刚度折减进程。为了在t0+Δt时刻更新损伤变量,定义t0+Δt时刻损伤变量为
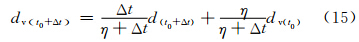
采用直径为16mm的冲头进行落锤冲击实验,冲击点为实验件的中央处,如图1所示。冲击完成后,测量冲击点处的凹坑深度,并使用超声C扫描测量损伤面积和损伤直径。
 | 图1 冲击位置 Fig.1 The position of impact | |
对复合材料加筋壁板进行建模。本模型将实验件分为两个部分:蒙皮和筋条。蒙皮采用连续壳单元SC8R,筋条采用实体单元C3D8R,两者用Cohesive(COH3D8)单元连接。蒙皮与筋条的厚度与铺层方式一致,厚度为2.75mm,铺层为[(45/-45/0/90/0)4/45/-45],层合板的单层厚度为0.125mm,共22层。对于ABAQUS软件,由于Hashin准则只能应用于壳单元,因此,对于筋条部分的损伤需要编写子程序(VUMAT)。实验件示意图如图2所示。
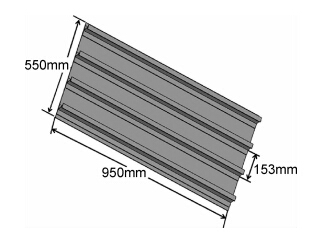 | 图2 实验件示意图 Fig.2 The sketch of test piece | |
冲头设为刚体,冲击点处进行网格细化。冲击能量分别选取10,15,20,25J。边界条件为蒙皮四边固支,复合材料加筋壁板的材料属性如表1所示。
| E1/MPa | E2/MPa | E3/MPa | ν12 | ν13 | ν23 | G12/MPa | G13/MPa |
| 135000 | 8800 | 8800 | 0.328 | 0.328 | 0.45 | 4470 | 4470 |
| G23/MPa | Xt/MPa | Yt/MPa | Xc/MPa | Yc/MPa | S12/MPa | S13/MPa | S23/MPa |
| 3260 | 1548 | 55.5 | 1226 | 218 | 89.9 | 110.5 | 110.5 |
本工作建立的仿真模型模拟了冲击过程中损伤的扩展情况,并计算了损伤区域的面积,如图3所示,红色区域ei≥1,即损伤区域,并与实验得到的无损检测C扫描图进行对比。由于冲击能量为10J的仿真结果与实验结果均没有出现损伤区域,因此将冲击能量为15,20,25J三个能量水平的损伤区域进行了对比。
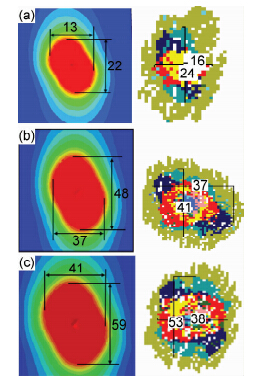 | 图3 损伤区域图 (a)15J;(b)20J;(c)25J Fig.3 The drawing of damage area (a)15J;(b)20J;(c)25J | |
由图3可以看出,由于复合材料结构各向异性,冲击损伤区域呈现出类似椭圆形状。且仿真得到的损伤区域与实验C扫描得到的损伤区域形状大致相同,损伤区域的最长和最宽处的比较接近。仿真与实验得出的损伤区域面积结果如表2所示。
| Impact energy/J | FEM result/mm2 | Test result/mm2 | Error/% |
| 10 | 0 | 0 | 0 |
| 15 | 203 | 235 | 13.6 |
| 20 | 1136 | 984 | 13.3 |
| 25 | 1568 | 1376 | 12.2 |
可以看出,模型计算得到的结果与实验结果相近,两者之间误差较小,说明建立的模型合理且有效。
3.2 冲击过程中的力学响应通过有限元计算得到不同冲击能量下接触力、复合材料加筋壁板吸收能量及损伤散逸能随时间的变化曲线,如图4所示。
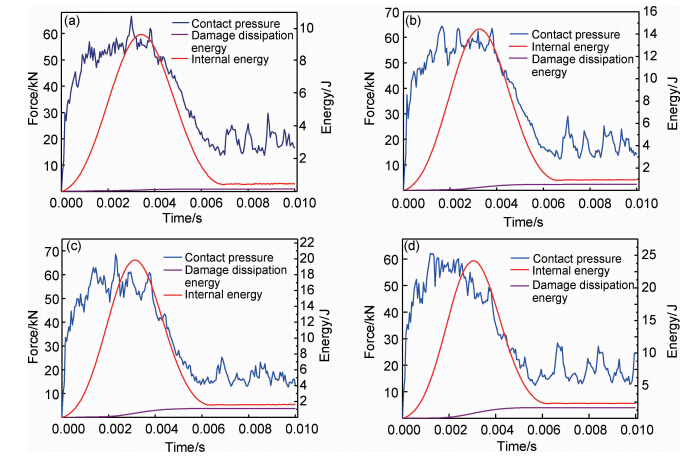 | 图4 冲击过程力学响应曲线 (a)10J;(b)15J;(c)20J;(d)25J Fig.4 Dynamics response curves in impact process (a)10J;(b)15J;(c)20J;(d)25J | |
在冲击过程的初始阶段,接触力随时间成线性增长,由于加入渐进损伤刚度退化方案,刚度矩阵出现衰减,接触力出现小幅振荡。当达到损伤判断准则时,复合材料加筋壁板开始出现损伤,刚度矩阵进一步衰减,接触力开始大幅度振荡。当能量增大到能够产生损伤时,损伤会耗散能量,接触力不再增加,出现一个平台,甚至损伤一开始便出现平台,没有线性上升。当冲击速度为0时,板吸收的能量达到最大值,但由于板的振荡波的存在,接触力在衰退的过程中仍然存在振荡。
对于能量的变化情况,随着冲头与板接触时间的增加,冲击能量逐渐转化为加筋壁板的内能,而当冲头的速度为0时,冲击能量为0,此时冲击能量绝大部分转化为加筋壁板的内能(少部分由于摩擦存在而转化为其他的能量)。此后,加筋壁板的内能随板的弹性变形和板的振荡动能而逐渐消失,但并没有完全消失。因为由于冲击载荷的作用,加筋壁板出现损伤散逸能,此部分能量随着损伤的出现而永久成为加筋壁板内能的一部分。
对于不同冲击能量,接触力、板的内能及损伤散逸能的变化曲线有所不同。由图4可以看出,冲击能量越大,在冲击速度为0时,板吸收的内能越大。不同冲击能量下,接触力峰值出现的时间也有所不同,对于10J冲击能量,接触力峰值与板内能最大值出现时间一致,而对于15,20J及25J的冲击能量,随着冲击能量的增大,接触力峰值较板内能出现时间变早,认为这是由于不同冲击能量对板的损伤程度有所不同,对于10J冲击能量,板几乎没有出现损伤,结构主要为弹性变形。由胡克定律可知,冲击速度为0时,板的变形最大,因此接触力也最大;而对于结构出现损伤的情况,刚度矩阵衰减,此时接触力峰值与变形量不成正比关系。对于25J冲击能量,损伤范围较大,刚度矩阵衰减严重,接触力峰值较板内能峰值出现早。本文认为,加筋壁板吸收的能量并不完全为损伤散逸能,还有部分用于产生板的永久变形(复合材料的“塑性变形”)。这体现在当冲击过程结束后,板的内能与损伤散逸能并没有完全重合。而不同冲击能量下两者之间的差值不同,冲击能量越大,两者之间的差值越大,具体如表3所示。
| Impact energy/J | Internal energy/mJ | Damage dissipation energy/mJ | Different value/mJ |
| 10 | 462.359 | 143.257 | 319.102 |
| 15 | 959.066 | 538.26 | 420.806 |
| 20 | 1631.27 | 1110.44 | 520.83 |
| 25 | 2279.19 | 1637.43 | 641.76 |
冲击过程中全部的冲击能量分配如图5所示。
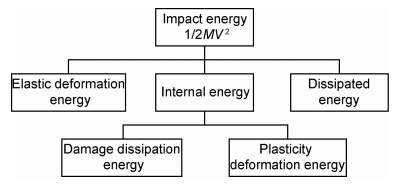 | 图5 冲击能量分配图 Fig.5 Distribution map of impact energy | |
落锤冲击实验后,进行了凹坑深度测量和C扫描无损检测,得到了不同冲击能量下凹坑深度和损伤面积与冲击能量的关系,如图6,7所示。凹坑深度和损伤面积的大小取决于冲击能量的大小,对于低速未穿透性损伤,两者之间基本呈线性关系,即冲击能量越大,凹坑深度越深,损伤面积越大。
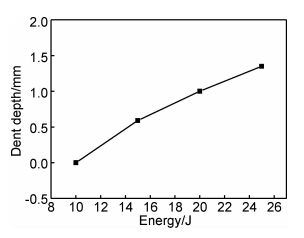 | 图6 凹坑深度与冲击能量关系 Fig.6 Dent depth versus impact energy | |
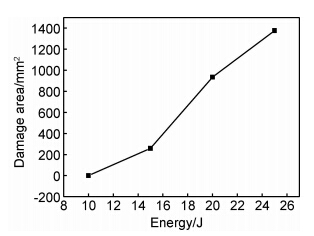 | 图7 损伤面积与冲击能量的关系 Fig.7 Damage area versus impact energy | |
(1)建立的仿真模型有效地模拟了低速冲击过程中加筋壁板损伤扩展情况,所得损伤区域与实验C扫描结果吻合较好,不同冲击能量下仿真结果与实验结果误差在13%左右。
(2)接触力在冲击开始阶段成线性增加,当加筋壁板出现损伤时,刚度矩阵衰减,接触力曲线发生振荡;随着冲击能量的增加,接触力峰值出现时间前移,并且板吸收的内能与损伤散逸能之间的差值变大。
(3)在低速未穿透冲击能量下,随着能量增大,凹坑深度与损伤面积具有较好的正相关关系。
| [1] | 中国航空研究院.复合材料结构设计手册[M].北京:航空工业出版社,2001.China Aviation Academy. Composite Material Structure Design Manual[M]. Beijing:Aviation Industry Press,2001. |
| [2] | DAVIES G A O, ZHANG X. Impact damage prediction in carbon composite structures[J]. International Journal of Impact,1995,16(1):149-170. |
| [3] | SCHOEPPNER G A, ABRATE S. Delamination threshold loads for low velocity impact on composite laminates[J]. Composites Part A:Applied Science and Manufacturing,2000,31(9):903-915. |
| [4] | FERABOLI P J, KEDWARD K T. A new composite structure impact performance assessment program[J]. Composites Science and Technology,2006,66(10):1336-1347. |
| [5] | FERABOLI P J, KEDWARD K T. Enhanced evaluation of the low-velocity impact response of composite plates[J]. AIAA Journal,2004,42(10):2143-2152. |
| [6] | FERABOLI P J. Some recommendations for characterization of composite panels by means of drop tower impact testing[J]. Journal of Aircraft,2006,43(6):1710-1718. |
| [7] | LOPES C S, CAMANHO P P, GURDAL Z, et al. Low-velocity impact damage on dispersed stacking sequence laminates.part II:numerical simulations[J]. Composite Science and Technology, 2009,69(8):937-947. |
| [8] | WANG Y Q, TONG M B, ZHU S H. Three dimensional continuum damage mechanics model of progressive failure analysis in fibre-reinforced composite laminates[A]. AIAA/ASME/ASCE/ AHS/ASC Structures,Structural Dynamics,and Materials Conference[C]. California:Palm Springs,2009. |
| [9] | 王一飞,张晓晶,汪海.复合材料层压板低速冲击响应与损伤参数关系研究[J].固体力学学报,2013,34(1):63-72.WANG Yi-fei, ZHANG Xiao-jing, WANG Hai. Low-velocity impact response of composite laminate and its relationship with damage parameters[J]. Chinese Journal of Solid Mechanics,2013,34(1):63-72. |
| [10] | 王仁鹏,陈普会,沈真.准静态压痕力作用下复合材料层压板的损伤阻抗分析[J].复合材料学报,2008,25(3):149-153. WANG Ren-peng, CHEN Pu-hui, SHEN Zhen. Damage resistance analysis of composite laminates subjected to quasi-static indentation[J]. Acta Materiae Compositae Sinica,2008,25(3):149-153. |
| [11] | 古兴瑾,许希武.复合材料整体化加筋壁板高速冲击损伤数值模拟[J].航空学报,2012,33(2):258-272. GU Xing-jin, XU Xi-wu. Numerical simulation of damage in stiffened integral composite panels under high velocity impact[J]. Acta Aeronautica et Astronautica Sinica,2012,33(2):258-272. |
| [12] | 严实,赵金阳,陆夏美,等.基于声发射技术的三维编织复合材料低速冲击损伤分析[J].材料工程,2014,(7):92-97. YANG Shi, ZHAO Jin-yang, LU Xia-mei,et al. Low-velocity impact response of 3D braided composites by acoustic emission[J]. Journal of Materials Engineering,2014,(7):92-97. |
| [13] | JOHNSON K L. Contact Mechanics[M]. New York:Cambridge University Press,1985. |
| [14] | HAGENBEEK M,HENGEL V C, BOSKER O J, et al. Static properties of fiber metal laminates[J]. Applied Composite Materials,2003,(10):207-222. |
| [15] | 伊鹏跃,于哲峰,汪海.复合材料层合板低速冲击刚度退化方案研究[J].力学季刊,2012,33(3):469-475. YI Peng-yue, YU Zhe-feng, WANG Hai. Stiffness degradation methodology for low-velocity impact simulation in composite laminate[J]. Chinese Quarterly of Mechanics,2012,33(3):469-475. |
| [16] | 张丽,李亚智,张金奎.复合材料层合板在低速冲击作用下的损伤分析[J].科学技术与工程,2010,10(5):1170-1174. ZHANG Li, LI Ya-zhi, ZHANG Jin-kui. Low-velocity impact damage analysis in composite laminates[J]. Science Technology and Engineering,2010,10(5):1170-1174. |
| [17] | LINDE P, PLEITNER J, BOER H, et al. Modeling and simulation of fiber metal laminates[A]. ABAQUS Users Conference[C]. California:Abaqus Inc,2004.421-439. |
 2015, Vol. 43
2015, Vol. 43


