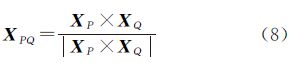1 引 言
地球椭球面上任意两点之间的最短距离为大地线,大地线是一条既有曲率又有扰率的空间曲线,不便于应用;而大椭圆是通过椭球面上两个已知点和椭球中心所作的平面切割椭球产生的截面椭圆,是与大地线十分接近的规则曲线,大椭圆算得的大地距离与用严密公式算得的大地线长相差极小[1, 2]。因此,按地球椭球面上的大椭圆航行是一种经济可行的远洋航法。然而传统的船舶远洋和极区航行一般采用沿地球球体上两点间的大圆弧即大圆航线航行。但是,地球实际上并不是一个标准的球体,而是一个近似的旋转椭球体。大圆航线设计阶段采用的球体模型和航行阶段现代导航设备采用的椭球体模型间不统一,使得船舶使用现代导航设备执行航行计划存在误差,影响船舶的正常航行和安全。大圆航线与大椭圆航线的航程误差,最大可达大椭圆航程的0.5%[3],在极区的相对误差也比其他地区偏大,因此为了满足现代导航对远距离、高纬度和高精度的要求,远洋和极区航行中航线的设计应该以规则的大椭圆为依据,以提高航线设计精度。
对大椭圆航线进行设计,首先需要计算两个大椭圆航线基本参数:大椭圆航程和大椭圆方位角,然后根据分点原则(等经差或等航程[4])求解分点坐标,最后计算出各分点间的恒向线航向和航程。本文主要针对前两个方面进行研究,目前研究大椭圆航线的方法与工作主要体现在以下方面:①将椭球面描写到球面上,采用球面几何的方法,解算大椭圆航程和航线坐标[5, 6, 7];②利用圆弧与大椭圆弧的对应关系,对大椭圆航程进行求解[8];③采用大地坐标系下的空间曲线方程及其曲线相关矢量的方法,计算大椭圆航线航程和方位角[9, 10];④采用位置矢量的方法,研究大椭圆航线航程、方位角和正反解问题[11, 12, 13];⑤采用单位速度矢量的方法,研究大椭圆航线航程、方位角和正反解问题[14, 15, 16]。从以上分析来看,空间矢量方法计算推导最为简洁,研究内容多关注于大椭圆导航中参数解算和航线方程正反解确定问题,在船舶大椭圆航线系统设计方面,尚需进一步研究以形成一套完善的大椭圆航线设计方法。
针对此问题,通过直接求解大椭圆顶点位置坐标,应用两个基本矢量推导大椭圆航线方位和航程计算公式,进而研究航线设计算法,重点研究基于Newton-Raphson(N-R)[17]等距离航线设计算法。
2 大椭圆描述方法 2.1 位置相关矢量[12]地球形状是一个凹凸不平的扁球体,为了获得精确航海计算的平滑地球模型,通常把地球近似为一个绕其短轴旋转的参考椭球体。如图 1所示,参考椭球表面上任意一点的位置可以用地理纬度φ和地理经度λ来确定,设参考椭球表面上一点P的坐标为(φ,λ),与之对应的位置矢量X可表示为
式中,RN为卯酉圈曲率半径;e为偏心率。

|
| 图 1 地球椭球体 Fig. 1 Earth ellipsoid |
同样,点P的位置也可以用地心纬度φ和地心经度λ(与地理经度数值相等)来确定,则点P的坐标又可表示为(φ,λ),位置矢量X也可表示为
式中,r为点P到参考椭球中心O的距离,即 式中,a为参考椭球长轴半径。由式(1)和式(2)相等得地理纬度和地心纬度的转换关系
根据地理经纬度与地球坐标系的关系,可得点P处的单位法线矢量TU、等纬度圈单位切线矢量TE和子午线单位切线矢量TN分别为
2.2 大椭圆顶点、长轴矢量和短轴矢量如图 2所示,弧为AB赤道半圆,参考椭球上任意两个点决定大椭圆,大椭圆的圆心在参考椭球的中心,长轴在大椭圆平面与赤道平面的交线上,长度为2a,短轴过椭圆圆心与长轴垂直。设P(φP,λP)和Q(φQ,λQ)为一个大椭圆上的两个点,满足φP、φQ不能同时为零且λP≠λQ,对应的位置矢量分别为XP和XQ,则大椭圆平面的单位法线矢量为

|
| 图 2 大椭圆顶点、长轴矢量和短轴矢量 Fig. 2 Vertex,major-axis vector and minor-axis vector of great ellipse |
大椭圆长轴既在大椭圆平面内又在赤道平面内,因此沿大椭圆长轴的一个单位矢量I0为
大椭圆短轴既与长轴垂直又与大椭圆的法线垂直,因此沿大椭圆短轴的一个单位矢量J0为
则大椭圆短轴与参考椭球在北半球的交点V的地心纬度满足考虑到短轴与参考椭球有两个交点,这里为了得到北半球的交点,因此对反正弦函数取绝对值。点V相应的经度为
将φV代入式(3),易知大椭圆短半径b为
由式(3)可知,北半球范围内大椭圆上的点与参考椭球球心的距离是关于纬度的减函数,短半径为该函数的最短距离,因此V点为大椭圆上纬度最高的点[18],即大椭圆的顶点。
定义大椭圆的长轴单位矢量I和短轴单位矢量J分别为
式中,I与I0相等或相反;J与J0相等或相反。但上述定义没有考虑两种特殊情况:一是当φP、φQ同时为零,此时大椭圆和赤道重合,可定义 二是当λP=λQ,此时大椭圆与子午圈重合,可定义采用长轴单位矢量I和短轴单位矢量J描述大椭圆,方便下文的公式推导和计算。
3 大椭圆航线航程和方位角 3.1 大椭圆航线航程计算大椭圆剖面图如图 3所示,其方程可以用式(17)的参数方程表示
式中,θ为矢量I绕中心O逆时针旋转到大椭圆上任意矢量X/|X|所需的角度,θ∈[0,2π),即 ρ=b/ 为大椭圆上一点到中心O的距离。
为大椭圆上一点到中心O的距离。

|
| 图 3 大椭圆剖面图 Fig. 3 Section of Great ellipse |
矢量aI对应的位置点沿大椭圆逆时针方向到矢量X对应的位置点的弧长S(θ)为
式(19)为椭圆积分,没有解析解,具体计算方法参考文献[2]。
P和Q分别为大椭圆航线的始点和终点,应用式(18)求出相应的θ角,分别为θP和θQ,考虑参考椭球上两点之间的大椭圆航线为劣弧,因此P和Q两点之间的航程为
3.2 大椭圆航线方位角计算大椭圆航线方位角(如图 4所示)通过计算大椭圆航线的单位切线矢量和子午线单位切线矢量的夹角进行求解。大椭圆航线上任意点处的一个单位切线矢量既垂直于大椭圆平面的法线又垂直参考椭球的法线,即

|
| 图 4 大椭圆航线方位角 Fig. 4 Azimuth of Great ellipse |
考虑到同一点处大椭圆航线的单位切线矢量有TGE和-TGE两种情况,因此大椭圆航线方位角也存在两种情况,即
4 大椭圆航线设计算法 4.1 等经差大椭圆航线设计算法大椭圆航线上任意一点的位置矢量X、长轴单位矢量I和短轴单位矢量J共面,因此满足
将式(2)和式(14)代入式(23),解得
将地心坐标转换为地理坐标得
根据等经差的分点原则确定分点经度后,利用式(25)确定分点纬度,然后计算出各分点间的恒向线航程和方位。
当大椭圆航线在赤道上或者子午圈上时,按大椭圆航线航行即按恒向线航行,无须进行大椭圆航线设计。
4.2 等距离大椭圆航线设计方法先根据式(20)求出总航程S,确定分点数量n,每段航程S为
则第i个分点与始点P的距离为
设第i个分点对应的位置向量为Xi,θ角为θi,P点对应的θ角为θP,则θi满足f(θi)=0,考虑多种情形,则
式(28)解析解可通过复杂的推导得到,也可以通过采用Newton-Raphson(N-R)方法[17]近似获得,即
如果在递推过程中出现θi,k∉[0,2π),通过判断θi,k所处的象限确定在定义域内对应的角度。很明显f′(θi)在f(θi)=0根θi附近不为零,f″(θi)存在,并满足
因此,N-R方法在θi∈[0,2π)上收敛,θi,0在区间[0,2π)上任意取值。
注意到椭圆的长、短半轴近似相等,很自然的把式(31)当成初始值
设置初始值同样会出现θi,0 [0,2π),通过判断θi,0所处的象限确定在定义域内对应的角度。
将式(18)和式(25)联立,可得
求出θi后,利用式(32),求解分点地心纬度及地理纬度,然后利用式(25)求分点经度,即
会出现λi∉[-π,π],也需要进行象限判断和确定。确定好分点纬度和分点经度,然后计算出各分点间的恒向线航程和方位。 5 算例分析为验证本文提出的大椭圆航线设计方法以及比较大椭圆航线和大圆航线设计差别,以非洲好望角(35°S,20°E)到澳大利亚墨尔本(38°S,145°E)之间的航线为例进行分析,大圆航线设计采用航海学半径为6 366 707 m的球体模型,大椭圆航线设计采用WGS-84参考椭球模型,分段恒向线航程和方位计算方法参照文献[19, 20],结果见表 1-3。
| 大椭圆航线 | 大圆航线 | |
| 总航程/n mile | 5 474.484 | 5 458.840 |
| 初始方位角 | 139°39′44″ | 139°47′23″ |
| 大椭圆航线 | 大圆航线 | |||||||||
| 分点经度/(°) | 分点纬度/(°) | 分段大椭圆航程/n mile | 分段恒向线航程/n mile | 分段恒向线方位/(°) | 分点经度/(°) | 分点纬度/(°) | 分段大圆航程/n mile | 分段恒向线航程/n mile | 分段恒向线方位/(°) | |
| 20.000 | -35.000 | 825.335 | 826.015 | 135.875 | 20.000 | -35.000 | 824.402 | 826.654 | 135.875 | |
| 32.500 | -44.890 | 629.327 | 630.021 | 127.141 | 32.500 | -44.890 | 627.727 | 629.616 | 127.141 | |
| 45.000 | -51.226 | 507.419 | 508.066 | 117.436 | 45.000 | -51.226 | 505.684 | 507.292 | 117.436 | |
| 57.500 | -55.121 | 437.811 | 438.412 | 107.197 | 57.500 | -55.121 | 436.096 | 437.525 | 107.197 | |
| 70.000 | -57.277 | 404.946 | 405.521 | 96.686 | 70.000 | -57.277 | 403.263 | 404.604 | 96.686 | |
| 82.500 | -58.062 | 401.322 | 401.894 | 86.080 | 82.500 | -58.062 | 399.645 | 400.975 | 86.080 | |
| 95.000 | -57.606 | 426.120 | 426.712 | 75.529 | 95.000 | -57.606 | 424.413 | 425.812 | 75.529 | |
| 107.500 | -55.832 | 484.985 | 485.618 | 65.199 | 107.500 | -55.832 | 483.248 | 484.801 | 65.199 | |
| 120.000 | -52.443 | 591.257 | 591.941 | 55.321 | 120.000 | -52.443 | 589.592 | 591.398 | 55.321 | |
| 132.500 | -46.835 | 765.961 | 766.656 | 46.277 | 132.500 | -46.835 | 764.768 | 766.921 | 46.277 | |
| 145.000 | -38.000 | - | - | - | 145.000 | -38.000 | - | - | - | |
| 总计/n mile | 5 474.484 | 5 480.856 | 5 458.840 | 5 475.599 | ||||||
| 大椭圆航线 | 大圆航线 | |||||||||
| 分点经度/(°) | 分点纬度/(°) | 分段大椭圆航程/n mile | 分段恒向线航程/n mile | 分段恒向线方位/(°) | 分点经度/(°) | 分点纬度/(°) | 分段大圆航程/n mile | 分段恒向线航程/n mile | 分段恒向线方位/(°) | |
| 20.000 | -35.000 | 547.448 | 547.615 | 137.320 | 20.000 | -35.000 | 545.884 | 547.084 | 137.325 | |
| 27.876 | -41.717 | 547.448 | 547.767 | 131.523 | 27.858 | -41.704 | 545.884 | 547.237 | 131.540 | |
| 37.480 | -47.768 | 547.448 | 548.031 | 123.595 | 37.448 | -47.752 | 545.884 | 547.504 | 123.621 | |
| 49.359 | -52.817 | 547.448 | 548.418 | 113.123 | 49.321 | -52.805 | 545.884 | 547.896 | 113.152 | |
| 63.826 | -56.400 | 547.448 | 548.800 | 100.208 | 63.794 | -56.395 | 545.884 | 548.282 | 100.227 | |
| 80.382 | -58.018 | 547.448 | 548.890 | 85.958 | 80.368 | -58.017 | 545.884 | 548.374 | 85.960 | |
| 97.387 | -57.374 | 547.448 | 548.602 | 72.258 | 97.395 | -57.373 | 545.884 | 548.081 | 72.245 | |
| 112.898 | -54.594 | 547.448 | 548.188 | 60.655 | 112.921 | -54.588 | 545.884 | 547.663 | 60.637 | |
| 125.903 | -50.122 | 547.448 | 547.866 | 51.650 | 125.926 | -50.112 | 545.884 | 547.338 | 51.636 | |
| 136.437 | -44.460 | 547.448 | 547.670 | 44.984 | 136.451 | -44.450 | 545.884 | 547.140 | 44.979 | |
| 145.000 | -38.000 | - | - | - | 145.000 | -38.000 | - | - | - | |
| 总计/n mile | 5 474.484 | 5 481.847 | 5 458.840 | 5 476.598 | ||||||
表 1为大椭圆航线和大圆航线航程和初始方位角结果比较。可以看出,大椭圆航线航程比大圆航线航程长15.644 n mile,初始方位角比大圆航线初始方位角小7′39″。
表 2为大椭圆航线和大圆航线等经差设计算法结果比较,可以看出,分点经度和分点纬度完全一样,分段恒向线方位几乎一样(误差量级为10-12°),但仅仅是数值上相等,由于采用地球模型不一致,其几何意义完全不同。除此之外,分段恒向线航程误差最大可达0.919 n mile,总航程误差达5.257 n mile。
表 3为大椭圆航线和大圆航线等距离设计算法结果比较,可以看出,大椭圆航线和大圆航线设计各参数均不相同,分点经度最大误差可达2′15″,分点纬度最大误差可达59″;分段恒向线方位最大误差可达1′42″,分段航程最大误差可达0.531 n mile,总航程误差达5.249 n mile。
大椭圆航线设计与航行阶段现代导航设备采用的椭球体模型保持一致,航线设计解算的参数与导航设备输出参数基准坐标系相同,除受风流影响外,能够较好地执行航行计划,而大圆航线设计阶段与航行阶段采用地球模型不一致,受此影响航行的执行会存在较大误差。通过以上结果分析可得,大圆航线设计采用球体模型会存在误差,主要体现在:航程和初始方位角参数存在误差;等经差航线设计算法对于两种航线的分点坐标和分段恒向线航向影响不大,而分段恒向线航程和总航程有较明显误差;等距离航线设计得到的各段参数均存在明显误差。因此,采用大椭圆航线设计算法代替传统的大圆航线设计算法,使得航线设计和航行阶段采用的地球模型一致,可以消除大圆航线计划阶段和航行阶段由于地球模型不同引起的误差,一定程度上提高了航海计算精度。
6 结 论本文提出了依据长轴矢量和短轴矢量的大椭圆描述方法,推导了大椭圆航线方位和航程计算公式,研究了航线设计算法,包括等经差航线设计算法和基于N-R方法的等距离航线设计算法。对比算例表明,大圆航线与大椭圆航线设计结果差异明显,而采用大椭圆航线设计与现代导航设备采用的地球模型相同,不会引起由模型差异导致的误差,因此大椭圆航线设计算法可以消除大圆航线计划阶段和航行阶段采用不同地球模型引起的误差,提高航海计算精度,且提出的算法可适用于航线设计的程序化设计。
| [1] | WILLIAMS R.The Great Ellipse on the Surface of the Spheroid[J]. Journal of Navigation, 1996, 49(2):229-234. |
| [2] | LI Houpu, WANG Rui. Great Ellipse Nautical Method and Its Navigation Parameters Calculation[J]. Journal of Naval University of Engineering, 2009, 21(4): 7-12. (李厚朴, 王瑞. 大椭圆航法及其导航参数计算[J]. 海军工程大学学报, 2009, 21(4): 7-12.) |
| [3] | EARLE M A. Sphere to Spheroid Comparisons[J]. Journal of Navigation, 2006,59(3): 491-496. |
| [4] | HONG Deben. Planning Ocean Route in the Way of Analytical Method [J].Journal of Dalian Maritime University, 1997, 23(4): 22-24. (洪德本. 解析法大圆航线的设计[J]. 大连海事大学学报, 1997, 23(4): 22-24.) |
| [5] | DING Jiabo. Study on the Relationship between Rhumb Line and Great Ellipse[J]. Tianjin Hanghai, 1994(2): 28-29. (丁佳波. 论等角航线和大椭圆之间的关系[J]. 天津航海, 1994(2): 28-29.) |
| [6] | DING Jiabo. Analytical Formula of Great Ellipse in Geographic Coordinate[J]. Tianjin Hanghai, 1993(2): 41-43. (丁佳波. 大椭圆地理坐标的解算公式[J]. 天津航海, 1993(2): 41-43.) |
| [7] | DING Jiabo. Distance Calculation Error between Great Circle Sailing and Great Ellipse Sailing[J]. Tianjin Hanghai, 1996(3): 3-4. (丁佳波. 大圆航法与大椭圆航法的航程计算误差[J]. 天津航海, 1996(3): 3-4.) |
| [8] | HE Yongqiang, LU Xin’gen, SHEN Chonghuan. Mathematical Model of Flight CouseⅠ[J]. Journal of Zhejiang Wanli University, 2001, 14(1): 4-8. (何永强, 陆新根, 沈重欢. 飞越北极数学建模方案Ⅰ[J]. 浙江万里学院学报, 2001, 14(1): 4-8.) |
| [9] | FANG Xuedong, HUANG Runqiu, WEI Guangxing. Calculation Method of FANS Route Based on Ellipsoid Model[J]. Journal of Southwest Jiaotong University, 2006, 41(4): 512-516. (方学东, 黄润秋, 魏光兴. 基于椭球模型的FANS航线算法[J]. 西南交通大学学报, 2006, 41(4): 512-516.) |
| [10] | FANG Xuedong.RNAV Route Planning with Regard to Earth Ellipticity[J]. Science of Surveying and Mapping, 2008, 33(6): 149-150. (方学东. 基于椭球模型的RNAV航路设计[J]. 测绘科学, 2008, 33(6): 149-150.) |
| [11] | EARLE M A. A Vector Solution for Navigation on a Great Ellipse[J]. Journal of Navigation, 2000, 53(3): 473-481. |
| [12] | EARLE M A. Vector Solutions for Azimuth[J].Journal of Navigation, 2008, 61(3):537-545. |
| [13] | EARLE M A. Accurate Harmonic Series for Inverse and Direct Solutions for the Great Ellipse[J]. Journal of Navigation[J]. Journal of Navigation, 2011, 64(3):557-570. |
| [14] | TSENG Weikuo, LEE Hsuanshih. Navigation on a Great Ellipse[J]. Journal of Marine Science and Technology, 2010, 18(3): 369-375. |
| [15] | TSENG Weikuo, GUO Jiunnliang, LIU Chungping. A Comparision of Great Circle, Great Ellipse and Geodesic Sailing[J].Journal of Marine Science and Technology, 2010, 21(3): 287-299. |
| [16] | SJÖBERG L E. Solutions to the Direct and Inverse Navigation Problems on the Great Ellipse[J]. Journal of Geodetic Science, 2012, 2(3): 200-205. |
| [17] | WU Yuanxin, WANG Ping, HU Xiaoping. Algorithm of Earth-centered Earth-fixed Coordinates to Geodetic Coordinates[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1457-1461. |
| [18] | NASTRO V, RANCREDI U.Great Circle Navigation with Vectorial Methods[J].The Journal of Navigation, 2010, 63(3): 557-563. |
| [19] | WANG Rui, LI Houpu. Symbolic Expressions of the Track Calculation Methods Based on the Ellipsoidal Model[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 151-155. (王瑞, 李厚朴. 基于地球椭球模型的符号形式的航迹计算法[J]. 测绘学报, 2010, 39(2): 151-155.) |
| [20] | GUO Yu.Navigation[M]. Dalian: Dalian Maritime University Press, 2011: 31-33. (郭禹. 航海学[M]. 大连: 大连海事大学出版社,2011: 31-33.) |