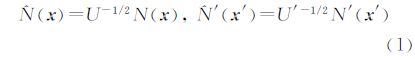2. 中国测绘科学研究院, 北京 100830
2. China Academy of Surveying & Mapping, Beijing 100830, China
影像配准是对取自不同时间、不同传感器或不同视角的同一场景的两幅或多幅影像进行最佳匹配的过程[1]，其在信息融合[2]、变化检测[3]等领域有着广泛的应用。影像配准主要包含影像匹配和配准模型建立这两个关键步骤。配准模型有多项式变换模型、透视投影变换模型等。常用的影像匹配方法可分为基于灰度和基于特征的方法[4]。基于上述影像匹配研究成果主要是针对影像变形不大的情况[5, 6, 7]，而对于存在较大仿射(透视)变形的倾斜影像的配准依然是目前的研究难点和热点[8, 9, 10]。
针对具有较大几何畸变的影像匹配问题，源于计算机视觉界的基于不变特征提取与描述的方法被广泛使用，如：文献[11]采用Harris算法提取特征并利用SIFT算法对特征进行描述匹配；文献[12]应用SIFT算法从海量特征数据库中识别目标特征。在此基础上，基于不同的出发点和思路，研究者们又提出了许多改进算法，如：文献[5]将多尺度Harris特征点和SIFT描述子相结合，提出一种基于场景复杂度与不变特征的航拍视频图像配准算法；文献[6]通过融合Harris-Affine与SIFT互补特征实现影像的自动配准；文献[13]利用影像间的几何关系对待配准影像进行粗纠正，在此基础上提出主方向改进的SIFT特征提取方法，实现了有较大差异的影像配准；为提高配准精度，文献[8]和文献[14]分别提出了基于SIFT和Harris特征点的高精度最小二乘匹配(least square matching,LSM)算法。对于存在较大几何变形的影像，应用LSM方法的关键是如何获得迭代参数初值。文献[8]的方法较好利用了SIFT特征尺度与方位信息作为最小二乘匹配迭代初值进行匹配优化；而文献[14]则是在仿射参数的量化空间内采用穷举搜索的方法来获得；文献[15]提出的两阶段影像配准算法，即首先采用基于SIFT的特征匹配方法进行粗配准以最大限度地消除影像间的几何变形，然后采用基于逐像素相关的方法来实现影像的精确配准。
为实现倾斜影像的高精度、稳健自动配准，上述方法存在如下缺陷：
(1) 多数研究采用的尺度不变特征点如多尺度Harris或SIFT特征点，当影像间存在较大的透视投影变形时，获得的匹配点较少甚至无法获得匹配。
(2) 最小二乘匹配迭代参数初值的获取过程较为复杂。相比于尺度不变特征，仿射不变区域特征对通常存在较大仿射(透视)变形的倾斜立体影像具有较好的适应性，然而文献[16]对现有的多种仿射不变特征的检测性能试验[16]表明：没有任何一种仿射不变特征能够适应所有不同类型、不同视点大小变化的影像。一般而言，MSER算法[17]能够提取图像中灰度一致的目标区域，而Harris&Hessian Affine[18](Ha&HeA)能够检测出灰度变化强烈的局部区域，因此，二者的有效融合可以获得更多的匹配特征，且利用其固有的区域仿射几何信息，易于为LSM迭代提供良好初值。
鉴于此，提出一种基于最大稳定极值区域(maximally stable extremal regions,MSER)与Ha&HeA的互补仿射不变特征高精度自动配准算法。算法在互补特征提取与优选的基础上，采用一种多层次自适应特征匹配算法来获得初始匹配，然后在基于同名仿射不变特征间的协方差矩阵与主梯度方位获得迭代参数初值的基础上，实现最小二乘匹配的迭代优化；最后基于投影变换模型实现影像之间的配准融合。实际影像数据试验证明了算法的有效性。
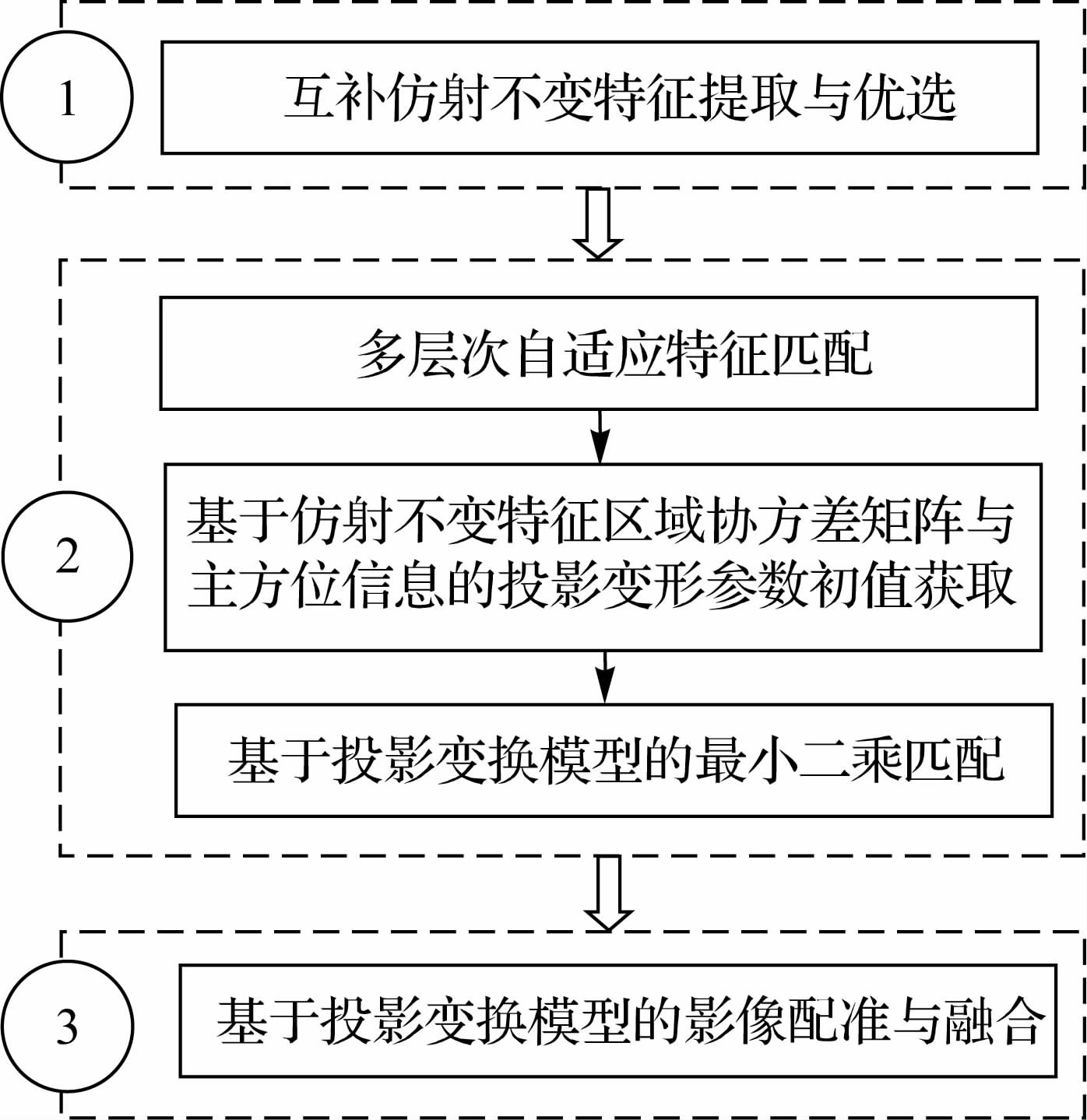
2 算 法本文算法流程如图 1所示。
|
| 图 1 本文算法流程 Fig. 1 Flow chart of the proposed algorithm |
(1) 特征提取。MSER提取算法借鉴地形中分水岭思想，首先对影像进行二值化聚类，获得众多极值区域，再根据极值区域的面积变化率检测得到MSER及其协方差矩阵。然后求取MSER重心作为特征坐标。MSER形状是任意的，为便于特征描述，进一步被拟合为椭圆形区域。Ha&HeA提取算法首先利用多尺度Harris&Hessian检测子提取初始特征点，即获得位置和尺度较为准确的初始估计，然后利用该特征协方差矩阵确定的椭圆表征局部各向异性结构，并由迭代过程来同步调整特征点的坐标和区域形状，收敛得到Ha&HeA特征。由上述可知，两种特征的提取原理差异较大，特征类型应具有较好的互补性，各提取算法分别详见文献[17, 18]。
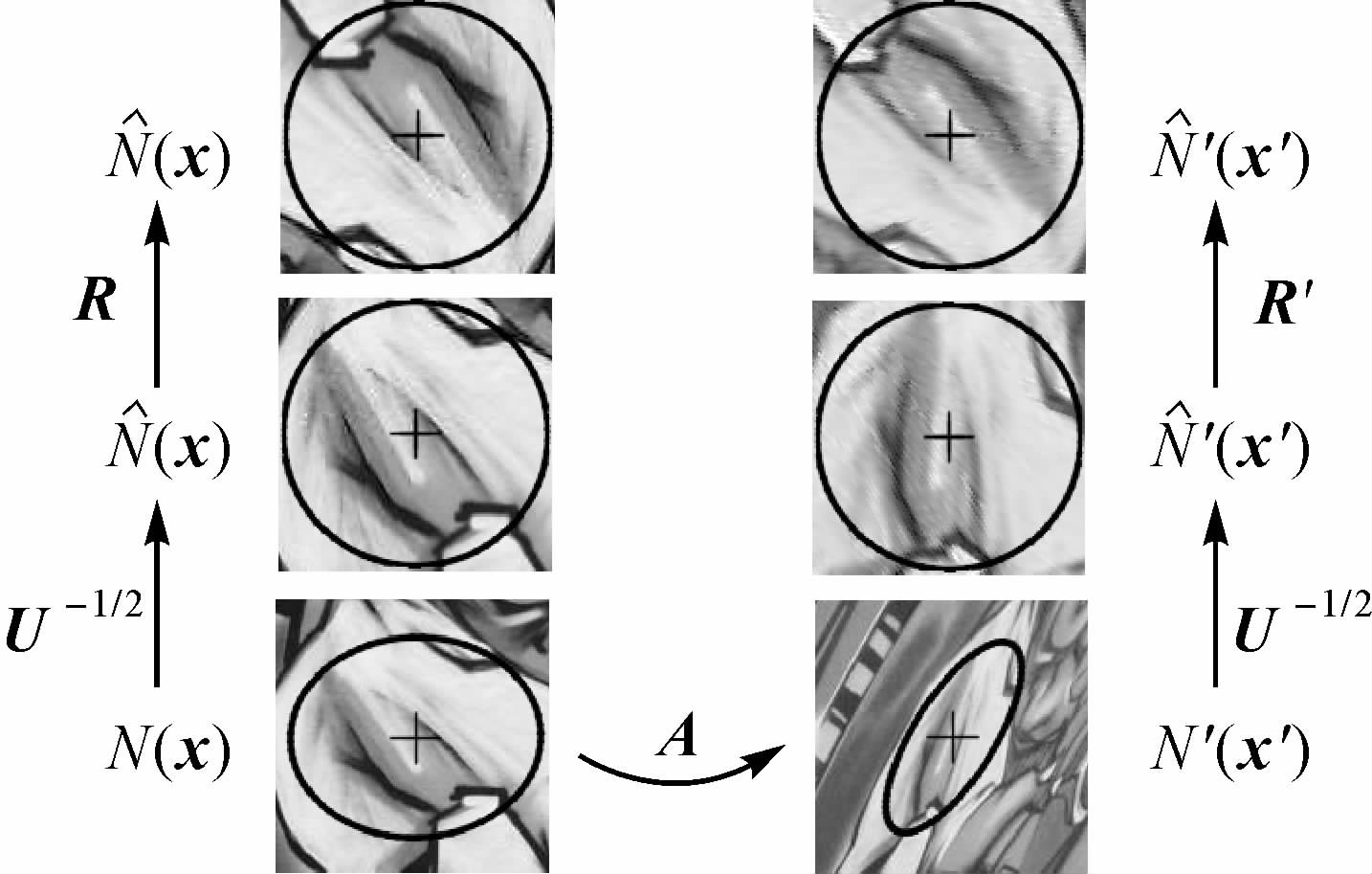
(2) 特征归一化。设f=(x,U)与f′=(x′,U′)为基准和待配准影像中任意同名特征，其中x、x′代表同名特征点坐标，U、U′为特征区域协方差矩阵，可分别唯一确定椭圆形特征区域N(x)和N′(x′)(见图 2)，其长短轴与长轴倾角值由各自协方差矩阵的特征值与特征向量求取。Ñ
(x)与<Ñ
′(x′)对应的归一化步骤如图 2所示：即首先利用式(1)进行仿射归一化，得到(x)与′(x′)，为克服方向奇异性，对(Ñ
x)与Ñ
′(x′)分别进行梯度直方图统计与曲线拟合，得到各自的主方位θ与θ′，按式(2)可构成旋转矩阵R与R′，(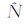
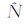x)与′(x′)再按式(3)分别进行旋转变换，得归一化区域(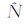x)与′(x′)
|
| 图 2 仿射不变特征归一化过程 Fig. 2 Normalization of invariant features |
(3) 特征描述。在归一化的区域中提取描述符。
2.1.2 互补不变特征优选
互补特征被提取后，特征区域交叠严重，这将在一定程度上影响匹配性能[19]。为此，采用如下步骤对特征进行优选：① 利用特征椭圆的长轴a与短轴b及其比率(10≤(a+b)/2≤80,a/b≤5)筛选中间尺度且稳定的特征；② 利用式(4)计算上步结果的信息熵均值H－ave，然后通过设定较小的全局熵阈值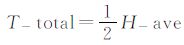
，过滤掉信息量明显差的特征；③ 根据特征点之间的欧氏距离，建立最小生成树(minimum spanning tree,MST)，再由距离约束关系完成特征分类。针对各类特征的优选方法为：按式(4)计算同类特征的H－avei，然后通过设定较高的熵阈值T－locali=H－avei，优选出同类中高信息熵特征，并保存最终的优选结果
采用一种多层次自适应策略来进行特征匹配，以最大限度地排除误匹配，具体步骤如下：
(1) 初始匹配。基于从归一化区域中已提取的SIFT描述符，并采用最/次近邻距离比率(nearest/next distance ratios，NNDR)测度来获得特征匹配。
(2) 基于自适应双重约束的相关系数匹配。基于式(5)采用随机采样一致性(random sample consensus,RANSAC)算法在剔除外点的同时估计基本矩阵F与单应矩阵Hg，其中，F描述了对应点之间应满足的极线约束条件；Hg则描述了对应点之间一一映射关系。然后，在对极与单应几何双重约束下，左右影像中经过归一化的不变特征，分别作为相关窗口W和W′，按式(6)进行相关系数匹配
式中，εF和εH分别代表匹配点到对应极线距离的均方根误差和单应矩阵的均方根误差；n为匹配点数。设定双重约束阈值
(3) 误差自适应的迭代匹配。在双重约束下按照步骤(2)的方法对初始特征重新进行匹配，保存特征匹配集并计算εF和εH，如果εF小于3.0像素并且εH小于4.0像素，则退出程序，否则重新执行步骤(2)。
(4) 重复步骤(3)，直至误差不再变化为止。
约束阈值系数k如果设置过小，容易出现匹配退化情况，试验表明，k取2.0为宜。NNDR测度阈值设为0.8，相关系数阈值设为0.75。
2.3 基于投影变换模型的最小二乘匹配 2.3.1 投影变形参数初值获取以特征点x为中心取大小为(2w+1)×(2w+1)的邻域。利用投影矩阵H近似x邻域与x′邻域窗口之间的几何变换关系，则有下式成立<
令
，则
。
其中，A表征邻域窗口间的仿射变形；t、v分别代表邻域窗口间平移与透视变形。进一步令u=[u,v]T∈[-w,w]，u′=[u′,v′]Τ为u按式(7)进行投影变换后的坐标。则以x和x′为中心的两个相关窗口W和W′可表达为
W与W′间的相关系数按上式(6)计算。注意，此处利用式(6)时，Wmn直接从影像中提取，W′mn则通过双线性插值得到。
基于式(8)，并进一步引入灰度补偿参数h0和h1，可建立基于投影变换模型的最小二乘匹配条件方程，线性化后可得最小二乘匹配的误差方程式[8]。误差改正矩阵ΔX=[Δh0,Δh1,Δa1,Δa2,…,Δa8]T包含了需要迭代估计的参数改正值。
相比于仿射变形，灰度、平移和透视变形相对较小，其相应的待求参数初始值可分别设置为h00=0，h01=1，a03=a06=a07=a08=0。因此投影变换参数初值获取问题进一步转化为如何求取仿射变换矩阵A的初值。
现以图 2为例，说明A的求取过程。前文已设N(x)与N′(x′)为同名区域，N(x)与N′(x′)之间的仿射变换关系可用式(9)表示。N(x)与N′(x′)按式(10)被分别归一化为(x)与′(x′)。
又由仿射几何知识可知，经归一化后的(x)与′(x′)的图像内容应一致，即(x)=′(x′)，因此，式(10)可进一步合并为
比较式(9)与式(11)，可得
2.3.2最小二乘匹配
LSM需要较为良好的待求参数初始值。对任意对特征匹配结果f与f′，便可用本文投影变形参数初值获取方法为最小二乘LSM提供初值，迭代求取最优的投影变换模型H。迭代终止条件可设为W、W′间相关系数ρ不再变化为止或达到预定的最大的迭代次数。迭代运算完成后，按式(13)对x′的坐标进行精确补偿。表 1给出了两组LSM投影变换窗口、相关系数ρ及匹配点投影误差ε(单位为像素)随迭代次数的变化，其中匹配点投影误差(利用已知的投影矩阵H0按式(14)计算得到
最小二乘匹配结束后，采用RANSAC算法进一步剔除粗差，得到最终匹配点。
2.4 基于投影变换模型的影像配准与融合由于投影变换模型比仿射变换更能严密地描述立体像对间的几何变换关系。因此，本文仍然选用式(7)表达的投影变换作为配准模型。利用最终的匹配点对作为配准控制点，采用最小二乘法求解式(7)中的8个投影变换参数。确定影像之间几何变换参数后，采样双线性插值方法，对参考影像进行重采样，并统一到基准影像的像素坐标系下，最终得到配准融合结果。
| 待匹配窗口 | 初值投影变换窗口 | 1次迭代 | 2次迭代 | 3次迭代 | 4次迭代 |
 | |||||
选取两组实际影像数据进行算法试验。第1组为存在70°视角变化的地面近景影像(记为Graf1、Graf2)，影像的投影矩阵H0已知，影像大小为800像素×640像素；第2组为存在约45°视角变化的无人机倾斜立体影像(记为UAV1、UAV2)，影像大小为1500像素×1500像素。各组试验人工选取15对检查点。第2组试验需要利用该组人工选取的检查点计算投影矩阵H0并视为已知。评价指标主要包括：① 正确匹配点数nε0，利用已知投影矩阵H0按式(14)计算匹配点投影误差，并对其设一阈值ε0，如投影误差小于ε0，则认为该点对为正确匹配，以此来统计正确匹配点数nε0。② 匹配正确率利用p=nε0/n计算，式中n代表匹配点总数。③ 配准误差εRMSE通过式(15)计算。式中xi与x′i为人工选取的检查点对，Hr为利用上文估算得到的投影配准模型
3.2 试验结果与分析
有5种方法被用于对比试验，分别是① 本文方法(proposed)；② ASIFT方法：全仿射ASIFT算法[20]是通过在对原始影像进行全方位模拟重采样基础上运用SIFT算法来实现的，虽可获得大量匹配点但运算复杂度较高，且在重复纹理区域容易出现误匹配，本文先利用ASIFT算法获得初始匹配，然后采用RANSAC算法估计投影矩阵，进一步剔除误匹配；③ Ha&HeA方法与④ MSER方法均采用本文多层次自适应特征匹配方法获得匹配点；⑤ 文献[6]方法：提取SIFT和Harris Affine特征，采用SIFT描述符与NNDR进行匹配，并利用马氏距离删除误匹配。
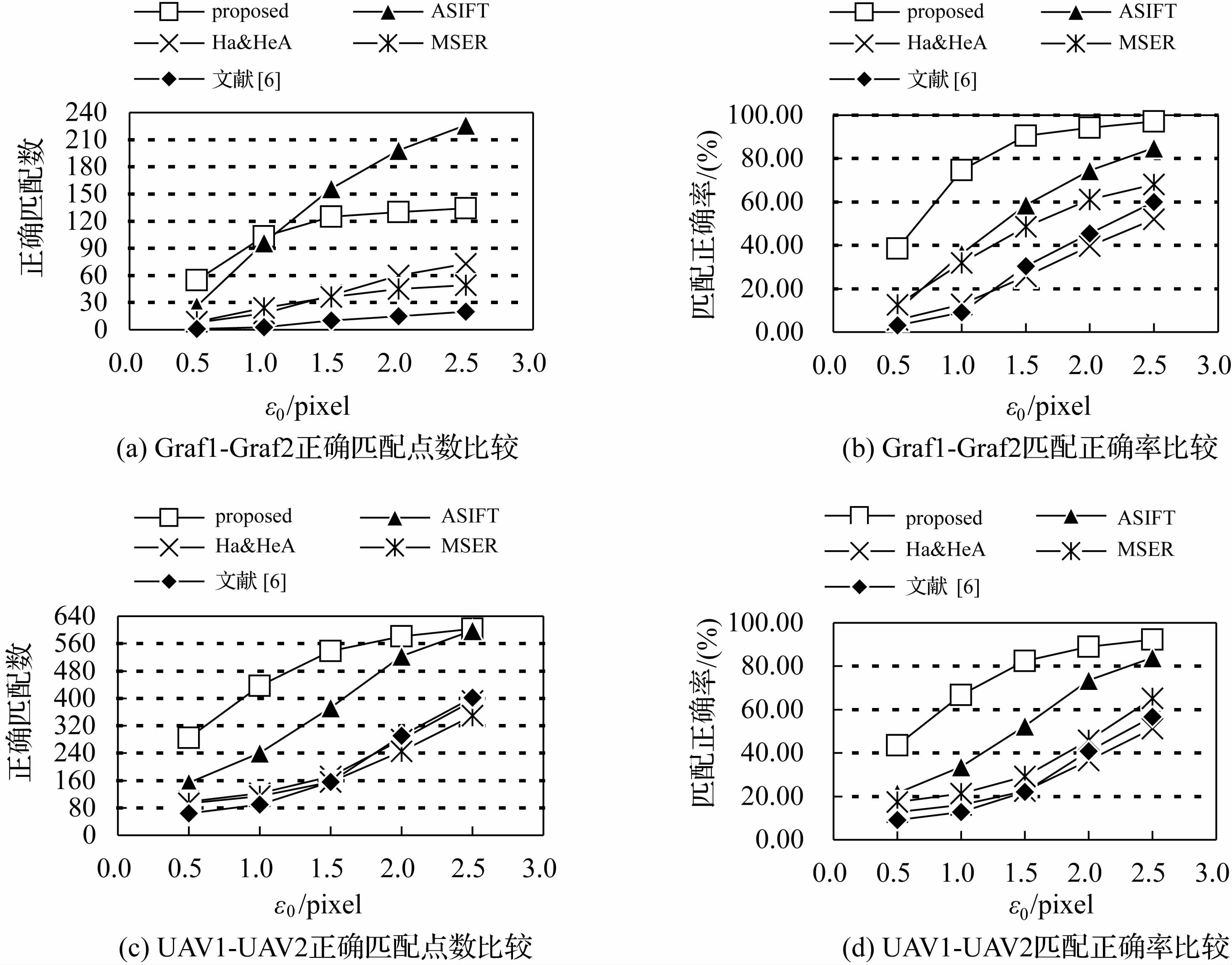
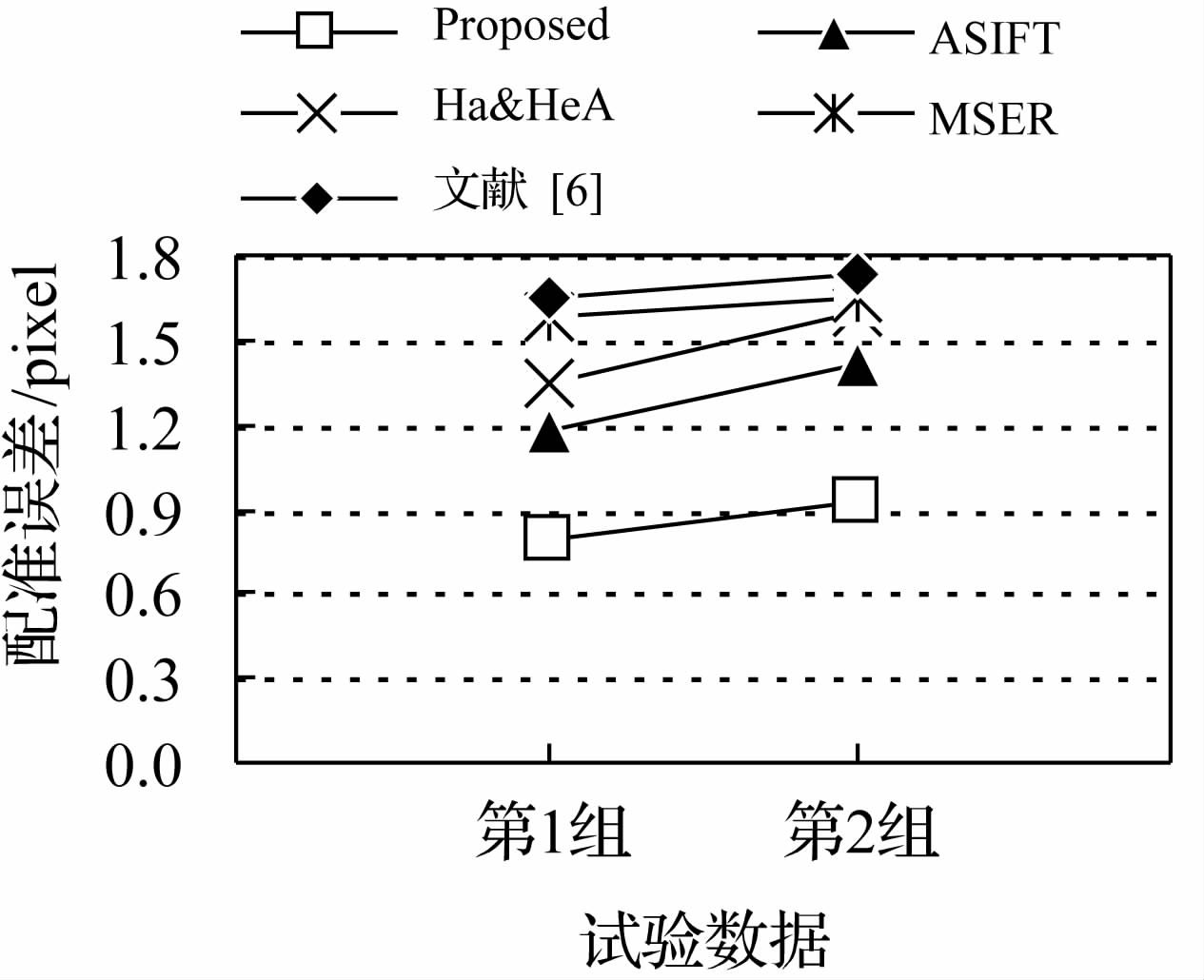
在配准过程中，离群点的剔除很关键，上述方法均采用了有效的误匹配剔除策略，以实现对各方法的客观评价。试验结果包括：① 图 6给出Graf1-Graf2与UAV1-UAV2分别利用各方法在ε0=2.5、2.0、1.5、1.0、0.5像素时正确匹配点数、匹配正确率结果；② 图 7给出Graf1-Graf2与UAV1-UAV2分别基于各方法的配准精度结果；③ 表 2给出本文算法由粗到精的匹配结果，表中n表示匹配点数，εRMSE为利用式(15)求取的配准误差，图 3给出本文方法的互补特征匹配结果与LSM精匹配结果。图 4给出ASIFT方法的匹配结果(为节省篇幅，其余方法的匹配结果不再给出)，图 5给出本文方法最终配准结果。
| 试验数据 |
|
| Graf1-Graf2 | 311 | 1.441 | 156 | 0.824 | 138 | 0.788 |
| UAV1-UAV2 | 1564 | 1.637 | 802 | 1.157 | 603 | 0.923 |
|
| 图 3 本文方法的匹配结果 Fig. 3 The matching results based on the proposed method |
|
| 图 4 ASIFT方法的匹配结果 Fig. 4 The matching results based on ASIFT method |
|
| 图 5 本文算法的配准结果 Fig. 5 Results of registration based on the proposed method |
综合上述试验结果，分析如下：
(1) 表 1表明，利用仿射不变特征区域协方差矩阵与主方位信息易于为LSM迭代提供良好的投影变形参数初值，显示出本文算法的鲁棒性。如表 1中第1组对应影像块之间即使存在70°的透视畸变，4次迭代后其相关系数为0.900，匹配精度达到0.371像素。然而，表 2说明，基于仿射不变特征匹配结果进行的LSM匹配，仍有部分点难以收敛，即使是LSM的精匹配结果，也会含有少量粗差点，分析原因，较复杂的仿射(透视)畸变数据与较多的辐射和几何畸变改正参数会影响到LSM匹配的收敛性及其收敛的可靠性。
(2) 对存在较大仿射(透视)变形的地面近景和低空倾斜立体影像，在较高的定位精度水平下，本文方法正确匹配点数与匹配正确率均优于其余方法。ASIFT方法虽能够匹配出许多同名像点，但其中能够达到子像素精度的同名点数却不及本文方法，原因在于本文采取两阶段紧凑匹配策略，即首先获取互补特征匹配，继而利用最小二乘匹配对特征匹配结果进行优化。由于特征检测与特征匹配的相对独立性，使得大多数特征匹配结果难以达到子像素级精度，如图 6 (a)所示的地面近景影像试验，在匹配定位精度水平从ε0=2.5像素提高到ε0=1.0像素过程中，ASIFT方法的匹配点被大量排除，而本文方法的匹配点仅有少量被排除，所以，在ε0=1.0像素时，本文方法的正确匹配点数开始占有优势；图 6 (c)所示的低空无人机影像试验表明，各定位精度水平下，本文方法的正确匹配点数均多于其余方法；图 6 (b)与(d)表明，随定位精度水平提高，本文方法的匹配正确率具有明显优势。
(3) 本文方法具有较高的配准精度。图 7直观地表明，针对不同类型的影像，本文方法均可达到子像素级的配准精度，而其余方法的配准精度则不及本文方法。由表 2可以看出，本文算法由粗到精的匹配，离群点被逐步排除，其中多层次自适应特征匹配的外点通过相关系数阈值排除，LSM阶段的外点通过其迭代收敛性排除，对LSM精匹配后可能包含的粗差点采用RANSAC算法排除。表 2还表明，针对LSM匹配结果并不完全可靠的问题，可采用RANSAC算法来进一步提高配准精度。
|
| 图 6 各方法在ε0=2.5、2.0、1.5、1.0和0.5像素时正确匹配点数、匹配正确率结果比较 Fig. 6 The correct matching number and correct rate with ε0=2.5、2.0、1.5、1.0 and 0.5 pixels for various methods |
|
| 图 7 配准精度结果比较 Fig. 7 Comparison of registration accuracy |
(4) 本文方法融合多种互补不变特征，有效保证了配准控制点的多量性和空间分布均匀性，继而提高配准的稳健性。图 3表明：集成多种互补不变特征匹配，与采用单一特征的MSER或Ha&HeA方法对比，能够显著增加不同类型的匹配区域，进而增加LSM精匹配点数，实现配准增强。另外，由图 4 (b)可以看出，低空无人机影像中部偏上的长条铁轨区域包含大量重复纹理，ASIFT方法的匹配点较少，而本文方法能够获得较多的Ha&HeA精匹配点(见图 3 (d))。
4 结 论针对存在较大仿射(透视)畸变的倾斜立体影像，先通过融合MSER与Harris&Hessian Affine多种仿射不变特征，能够获得较多的特征匹配；继而基于仿射不变特征区域协方差矩阵与主方位信息易于获取LSM匹配初值，通过迭代达到对原始特征匹配误差的精确补偿。试验结果表明本文方法在正确匹配点数、匹配正确率、匹配点分布的均匀性以及配准精度方面具有优越性，因此本文为倾斜影像的高精度配准探索了一种可行的思路。但本文算法仅对平面场景和地形较平坦区域进行试验验证，把互补匹配点由单平面场景匹配传播到多平面场景中是本文下一步要研究的内容。
| [1] | BROWN L. A Survey of Image Registration Techniques [J]. ACM Computing Surveys, 1992, 24(4): 325-376. |
| [2] | MARCELLO J, MEDINA A, EUGENIO F. Evaluation of Spatial and Spectral Effectiveness of Pixel-level Fusion Techniques [J]. IEEE Geosciences and Remote Sensing Letters, 2012, 10(3): 432-436. |
| [3] | KIM Y S, LEE J H, RA J B. Multi-sensor Image Registration Based on Intensity and Edge Orientation Information [J]. Pattern Recognition, 2008, 41: 3356-3365. |
| [4] | ZHANG Qian, LIU Zhengkai, PANG Yanwei, et al. Automatic Registration of Aero Photos Based on SUSAN Operator [J]. Acta Geodaetica et CartoGraphica Sinica, 2003, 32(3): 245-250. (张迁, 刘政凯, 庞彦伟, 等. 基于SUSAN算法的航空影像的自动配准[J]. 测绘学报, 2003, 32(3): 245-250.) |
| [5] | YANG Tao, ZHANG Yanning, ZHANG Xiuwei, et al. Scene Complexity and Invariant Feature Based Real-time Aerial Video Registration Algorithm [J]. Acta Electronic Sinica, 2010, 38(5): 1069-1076. (杨涛, 张艳宁, 张秀伟, 等. 基于场景复杂度与不变特征的航拍视频实时配准算法[J]. 电子学报,2010, 38(5): 1069-1076.) |
| [6] | LI Lingling, LI Cuihua, ZENG Xiaoming. An Automatic Image Registration Method Based on SIFT and Harris-Affine Features Matching [J]. Journal of Huazhong University of Science & Technology, 2008, 36(8): 13-16. (李玲玲, 李翠华, 曾晓明. 基于Harris-Affine和SIFT特征匹配的图像自动配准[J]. 华中科技大学学报:自然科学版, 2008, 36(8): 13-16.) |
| [7] | LUO Nan, SUN Quansen, GENG Leilei, et al. An Extended SURF Descriptor and Its Application in Remote Sensing Images Registration [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 383-388. (罗楠, 孙权森, 耿蕾蕾, 等. 一种扩展SURF描述符及其在遥感图像配准中的应用[J]. 测绘学报, 2013, 42(3): 383-388.) |
| [8] | YANG H C, ZHANG S B, WANG Y B. Robust and Precise Registration of Oblique Images Based on Scale Invariant Feature Transformation Algorithm [J]. Geoscience and Remote Sensing Letters, 2012, 9(4): 783-787. |
| [9] | ANTONIO M G, TOMMASELLI, MAURICIO G, et al. Generating Virtual Image from Oblique Frames [J]. SIAM Journal on Imaging Sciences, 2013, 5(4):1875-1893. |
| [10] | PODBREZNIK P, POTOCNIK B. A Self-adaptive ASIFT-SH Method [J]. Advanced Engineering Informatics, 2013, 27(1):120-130. |
| [11] | QIU Jianguo, ZHANG Jianguo, LI Kai. An Images Matching Method Based on Harris and Sift Algorithm [J]. Journal of Test and Measurement Technology, 2009, 23(3): 271-274. (邱建国, 张建国, 李凯. 基于Harris与Sift算法的图像匹配方法[J]. 测试技术学报, 2009, 23(3): 271-274.) |
| [12] | JIA Shijie, WANG Pengxiang JIANG Haiyang, et al. Study of Image Matching Algorithm Based on SIFT [J]. Journal of Dalian Jiaotong University, 2010, 31(4): 17-21. (贾世杰, 王鹏翔, 姜海洋, 等. 基于SIFT的图像匹配算法[J]. 大连交通大学学报, 2010, 31(4): 17-21.) |
| [13] | YUE Chunyu, JIANG Wanshou. An Automatic Registration Algorithm for SAR and Optical Images Based on Geometry Constraint and Improved SIFT [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 570-576. (岳春宇, 江万寿. 几何约束和改进的SIFT的SAR影像和光学影像自动配准方法[J]. 测绘学报, 2012, 41(4): 570-576.) |
| [14] | XIAO J J, SHAH M. Two-frame Wide Baseline Matching[C]//Proceedings of IEEE Conference Computer Vision, Nice:[s.n.], 2003: 603-609. |
| [15] | MONTOLIU R, PLA F. Generalized Least Squares-based Parametric Motion Estimation [J]. Computer Vision and Image Understanding, 2009, 113: 790-801. |
| [16] | MIKOLAJCZYK K, TUYTELAARS T, SCHMID C. A Comparison of Affine Region Detectors [J]. International Journal of Computer Vision, 2005, 60(1):163-186. |
| [17] | MATAS J, CHUM O, URBAN M, et al. Robust Wide-baseline Stereo from Maximally Stable Extremal Regions [J]. Image Vision Computing, 2004, 22(10): 76-767. |
| [18] | MIKOLAJCZYK K, SCHMID C. Scale & Affine Invariant Interest Point Detector [J]. International Journal of Computer Vision, 2004, 60(1):63-86. |
| [19] | CHENG Liang, GONG Jianya, SONG Xiaogang, et al. A Method for Affine Invariant Features Extraction with High Quality for Wide Baseline Stereo Image Matching [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 77-82. (程亮, 龚健雅, 宋小刚, 等. 面向宽基线立体影像匹配的高质量仿射不变特征提取方法[J]. 测绘学报, 2008, 37(1): 77-82.) |
| [20] | MOREL J M, YU G S. ASIFT: A New Framework for Fully Affine Invariant Image Comparison [J]. Siam J. Imaging Sciences, 2009, 2(2): 438-469. |