2. 西安测绘研究所,陕西 西安 710054;
3. 西安测绘信息技术总站,陕西 西安 710054;
4. 65051部队,辽宁 大连116031
2. Xi’an Institute of Surveying and Mapping, Xi’an 710054,China;
3. Xi’an Technical Division of Surveying and Mapping, Xi’an 710054,China;
4. 65051 Troops, Dalian 116031,China
在我国大地测量产品序列中,坐标转换格网模型是2000中国大地坐标系(CGCS2000)[1, 2, 3, 4]启用后,继重力异常格网模型、高程异常格网模型和垂线偏差格网模型之后又一新的大地测量数字格网模型产品形式。
坐标转换格网模型是一定范围内两坐标系坐标分量差值的离散化数字表达,是该范围内所有等间距格网点坐标分量差计算值的集合,在数据库中以格网数据结构的形式存储。格网数据结构是把建库的地理范围按经纬线划分成规则的梯形格网,以格网的纵横交点作为节点,存储对应于该交点的坐标分量差值。
坐标转换格网模型在国际上已有20多年的应用历史。美国1927北美基准(NAD27)至1983北美基准(NAD83)的转换最先采用了这一方法[5],该方法的转换精度在美国主要大陆地区为±0.15m[6],满足了测量和制图等工作的需要。后来日本[7]、新西兰[8]、澳大利亚[9]、加拿大[10]等国也相继构建了格网坐标转换模型,不同的是在构建格网模型时,根据本国的实际采用了不同的数学方法,如最小曲率法、最小二乘配置法、多元回归法等。除了经典大地坐标系与现代大地坐标系的转换外,美国还建立了NAD83向高精度区域网(HARN)转换的格网模型,由于HARN是美国各州建立的,所以几乎每个州都有一套格网模型。目前常用的GIS软件(如ArcGIS)中,内置有格网坐标转换模型,许多国家的坐标转换格网文件存储在安装目录下,用户可直接调用。在我国,对于坐标转换的数学模型已有了较深入的研究[11, 12, 13, 14, 15, 16],但对用于地图坐标变换的坐标转换格网模型的研究和应用还刚起步。
针对我国CGCS2000启用后坐标转换应用的多类型,可按精度指标分3类构建我国坐标转换模型产品,一是用于大众化导航应用的低精度转换,坐标分量精度为±5~±10m;二是用于三维坐标相似转换的中精度转换,坐标分量精度为±0.5~±5m;三是用于地形图图廓线和坐标网转换的高精度转换,坐标分量精度不超过±0.5m。本文针对高精度转换应用类型,阐述了我国CGCS2000高精度坐标转换方法,讨论了坐标转换最小曲率方程,提出了格网节点迭代计算方法和区域性格网模型的建立方法,构建了格网模型数据结构,给出了全国范围CGCS2000高精度坐标转换格网模型的最优格网间距和转换精度。CGCS2000高精度坐标转换格网模型已在全国1∶25万和1∶5万地形图更新生产等工程中应用。
2 坐标转换格网模型的高精度建立某区域的坐标转换格网模型就是把该区域按经纬线划分成等间距的规则格网单元,根据区域内公共点上已知的坐标分量差值,采用一定的数学模型(如最小曲率法)求得各个格网节点的坐标分量差。坐标转换格网模型能实现高精度的坐标转换,理由如下:
分析产生两坐标框架间坐标差异的原因,可分为以下3类:一是两坐标系的定义差,二是建立该两坐标框架(即大地控制网)时的局部性系统误差,三是建立该两坐标框架时的偶然误差。对于偶然误差,如控制点的坐标值一经确定,则观测偶然误差也将以系统性偏差的特性对控制测图产生影响,而这类误差是非常复杂的。文献[17]针对卫星导航数据的误差特性也作过类似的分析。因此,综合这3类偏差,要用一个数学公式构建高精度坐标转换模型是不可能的。坐标转换格网模型将数学模型和数字模型有机结合,可以高精度地拟合两坐标框架间的各种偏差,从而实现高精度的坐标转换。
3 最小曲率法坐标转换格网模型 3.1 坐标转换最小曲率方程
建立格网模型的数学公式较多,有最小二乘配置法、多元回归法、相似变换、最小曲率法等[18],单从转换精度看,这些模型相差不大。如果某一模型的精度不够,可通过改进计算策略、缩小搜索半径来提高精度。例如文献[13, 14]采用相似变换模型通过缩小分区范围也可获得很高的转换精度。但采用最小曲率法还可得到很好的光滑性。
在第2节中分析的坐标差异产生的3类原因中,定义差和大区域性的系统偏差导致的差异在地理空间是平滑改变的,曲率也是连续的,体现为整体性的光滑;小区域性的系统偏差和测量中的偶然误差导致的差异则为局部性,体现为局部性的光滑。
通过最小曲率法建立最小曲率格网曲面来拟合坐标之间的差异,能够同时满足整体光滑和局部光滑的要求。
把格网化的坐标位移值所属地理区域比作一块大的薄片,各点都对这个薄片施加垂直方向上的拉力,则薄片会发生弯曲和变形,每个点上变形的幅度取决于在这个点上施加的力,距离点较远处的变形则取决于临近的拉力,显然,点之间的弯曲是平滑的。点上的坐标位移值等同于点上施加的向上的拉力,位移表面的平滑弯曲代表着各个位置的坐标位移。
描述平面变形的双谐偏微分方程为
式中,fn为施加的力;L、B为点位的经纬度坐标;u为位移量(分别取两坐标系的经差ΔL、纬差ΔB、大地高差ΔH)。式(1)的解是一个二维空间变量的三阶多项式,要求观测点上的位移值等于观测值,即 式中,u(Lm,Bm)是观测点m处的位移量;wm是点m处的观测值,分别取m点两坐标系的经差ΔLm、纬差ΔBm、大地高差ΔHm。对于一个平面来说,认为边界外不存在外力,且曲面在边界法线方向上弯曲率为0,即 为边界条件。
格网点(Li,Bi)上的曲率是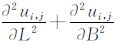 ,取所有格网节点的曲率平方和为极小,可推导出计算格网节点的估计值ui,j的差分方程[19]
,取所有格网节点的曲率平方和为极小,可推导出计算格网节点的估计值ui,j的差分方程[19]
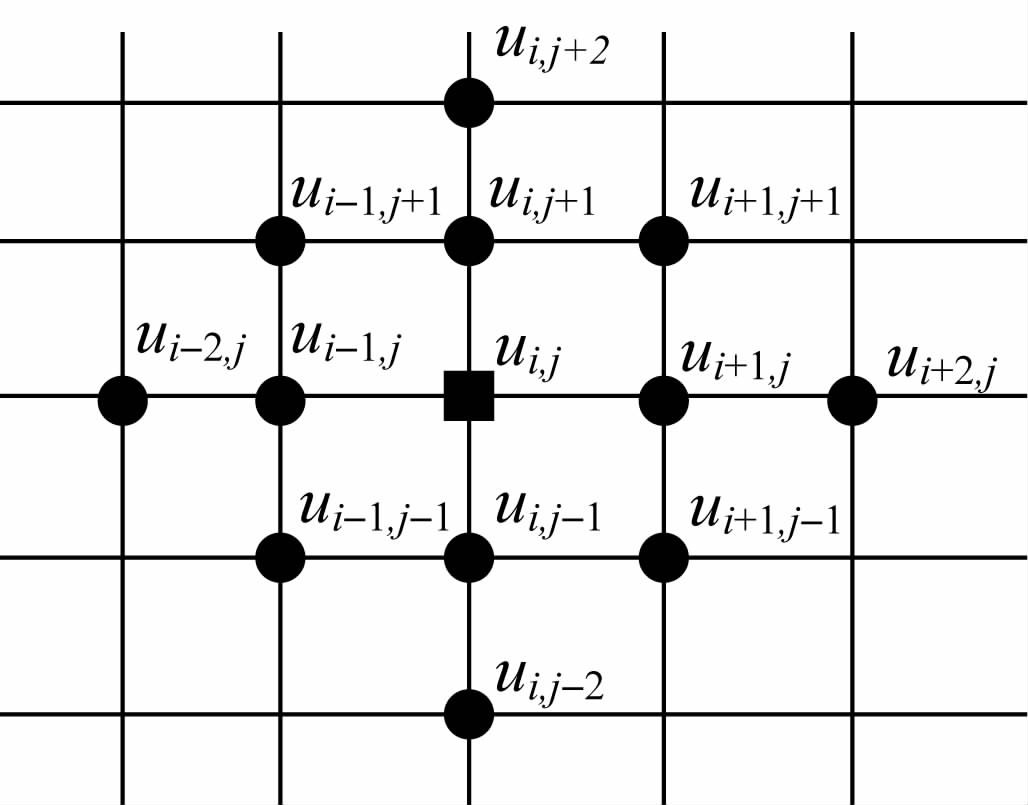
可见要求当前节点的基准位移值ui,j,需知道周围其他12个节点的基准位移值(见图 1)。
|
| 图 1 差分方程中的节点布局 Fig. 1 The nodes distribution in difference equation |
式(4)适用于离开边界且周围没有观测点的情况。当格网节点位于边界上或附近有观测点,则格网节点的曲率计算公式需要作相应的调整[19, 20]。
由上可知,用最小曲率法生成的插值面类似于一个通过各个数据值的具有最小弯曲量的薄弹性片。最小曲率法试图在尽可能严格地尊重数据(见式(2))的同时,生成尽可能光滑的曲面(见式(4))。式(4)的效果与分段连续样条函数一样,可以同时模拟整体和局部光滑。而采用其他数学模型(如多元回归[18]、分区七参数模型[13, 14]等)建立格网,节点值是采用该节点搜索半径范围内的观测值来计算的,转换精度虽然很好,但并不顾及节点间的光滑性。
3.2 格网节点的最小曲率法迭代计算
由式(4)可知,计算每个节点都要用到邻近的其他节点,所以为了解出差分方程,需要给所有节点赋初值,且进行迭代计算。
迭代时,从代表长波趋势的粗格网开始,在两维方向上逐次加密格网,每次加密格网都需要迭代,这样可以兼顾整体光滑和局部光滑的要求。格网间隔的选择极为重要,间隔过于稀疏会混淆数据,间距过密将不能真实地描绘区域趋势。但究竟该取多大的格网间距才算最优,只能根据多次试验结果,依据我国大地控制网的实际情况确定。
将粗格网细化的方法按如下步骤实现:
(1) 确定最优格网间距以及划分的格网数。为了减少各向异性误差的影响,将二维方向的格网间距取成一致。
(2) 确定粗格网的格网间距。为了能使用差分方程,第一次按粗格网间距划分的格网数必须大于等于4,而且能整除最优格网的格网数。
(3) 依次细化粗格网直到达到最优格网。第一次所用的粗格网节点的初值可以用离格网节点最近的观测值,或者由周围的观测值加权得到。迭代过程中加密格网产生的新格网的初始值可通过上一次细化的粗格网线性内插来获得。初始值越接近渐进可展解的值,所需迭代的总次数就越少。
3.3 格网模型的数据结构通过格网模型构建了描述两坐标框架差异空间分布的有序数值阵列,它是表示区域D内的3个三维向量有限序列组
式中,Li、Bi是第i个格网点的平面坐标;ΔLi、ΔBi、ΔHi是两坐标系的坐标差值。当该序列中各平面位置格网呈规则排列时,其平面坐标可省略,因每一个格网点与其他相邻格网点之间的拓扑关系都隐含在该阵列的行列号当中。此时式(5)就简化为一维向量序列组 在地图和影像等产品的生产应用中,只需要平面基准的转换,而不需要大地高的转换,因而式(6)只取前两式。从实用的角度看,采用两维方向间距相同的正方形格网在数据处理方面有很多优点,一是结构简单,除了每个格网点处的坐标分量偏差外,只需要记录一个起算点的位置坐标和格网间距,数据存储量很少;二是计算方便,可以根据该区域的原点坐标和格网间距,对相应矩阵元素的行列号经过简单的运算而获得任意格网点的平面位置;三是适合于实时服务以及大规模使用和管理,可以借助于简单的格网数据处理方法进行数据压缩处理,如行程编码法、四叉树法、多级格网法和霍夫曼码法等。
格网坐标转换模型数据文件包括3个逻辑部分:① 元数据,指描述格网坐标转换模型一般特征的数据,如名称、边界、构建单位、精度等参数;② 数据头,定义格网坐标转换模型的起点坐标、坐标类型、格网间隔、行列数等;③数据体,沿行列分布的坐标分量偏差值数字阵列。
格网坐标转换模型数据库按分块层次结构建立空间索引实现格网数据的快速查找、存取和计算操作等。按国家标准图幅大小进行块的划分,一个块就是一幅图的范围,末级子块由若干行和若干列的格网单元组成。通过行列结构索引,便可唯一确定格网坐标转换模型数据库范围内任意空间位置的坐标偏差值。由这种分块和行列层次划分形成的空间索引可以保证格网坐标转换模型数据的快速查找和无缝存取。
格网模型可采用多级格网结构,不同级格网间距不同,格网越小,所表达的连续坐标分量差值的分辨率越高。例如,将建库地区根据已知数据的分布分为多个区域,不同区域采用不同间距的格网。
4 全国范围CGCS2000坐标转换格网模型的建立 4.1 最优格网间距的选取
以一幅典型的1∶50万地形图幅为例说明最优格网间距的选取试验。该图幅范围内(34°B~36°B,114°L~117°L)有410个全国天文大地网与空间大地网联合平差点,这些公共点具有1954北京坐标系(BJS54)、1980西安坐标系(XAS80)和CGCS2000坐标,数据点的平均间距约为7.2′(约13km)。按照每10个点中取1点的方式均匀提取41个点作为检核点,剩下的369个点建立模型。
按照最小曲率法建立格网模型的方法,采取不同格网间距,分析格网间距的差异对最终转换精度的影响。
| 坐标转换 | 格网 间距 |
|
| BJS54 → CGCS2000 |
|
| XAS80 → CGCS2000 |
|
| 坐标转换 | 格网 间距 |
|
| BJS54 → CGCS2000 |
|
| XAS80 → CGCS2000 |
|
由最小曲率方程可知,理论上表 1的内符偏差值应为0,实际上由于求内插点值时采用了线性内插,故使之不为0。因而,表 1的内符偏差反映了格网点和内插点之间的坐标差值存在非线性变化的程度。
由表 2可知,转换精度与格网密度相关,在观测数据分辨率范围内,格网间距越小,转换精度越好,但格网密度超过观测数据分辨率时,受高频振荡影响,转换精度反而会变差。
表 2中,BJS54到CGCS2000的转换,格网间距为2.5′×2.5′时,转换精度已经很好,继续加密取1.5′×1.5′时已经没有改进,外符精度反而变差了。说明在2.5′×2.5′范围内,两坐标系差值的变化已比较平缓,按线性内插已基本符合实际情况。因此2.5′×2.5′的格网间距应该作为BJS54到CGCS2000转换的最佳选择。
表 2中,XAS80到CGCS2000的转换,格网间距为3.0′×3.0′时,转换精度已经很好,取2.5′×2.5′时已经没有改进,外符精度反而会变差。说明我国天文大地网经整体平差后局部精度也已提高。因此3.0′×3.0′的格网间距应该作为XAS80到CGCS2000转换的最佳选择。
由此可见,我国大地网的最优格网间距大约为公共点平均间距(7.2′)的0.3倍到0.4倍(4~5km),在这一尺度上,任一点的大地坐标改正值可按双线性内插方法获得。
4.2 格网模型的构建
以全国天文大地网与空间大地网联合平差建立的2000国家大地控制网[21]的48433个点为观测量,建立最小曲率法坐标转换格网模型。格网间隔统一取为2.5′×2.5′。对于XAS80,因3.0′×3.0′与2.5′×2.5′的结果差别不大,为实用方便,也取为2.5′×2.5′。计算结果见表 3。
| 坐标转换 | 格网间距 | 公共点数 | 中误差/m | |
| B分量 | L分量 | |||
| BJS54 →CGCS2000 | 2.5′×2.5′ | 48 433 | 0.062 | 0.071 |
| XAS80 →CGCS2000 | 2.5′×2.5′ | 48 433 | 0.006 | 0.012 |
将2000国家大地控制网48433个点按经纬度排序,每隔100点选取1点,在全国范围共选出484个点作为外部检核。剩余47949个点为观测量,建立2.5′×2.5′间隔的格网模型。将未参与构建格网模型的484个点的BJS54(或XAS80)坐标按所建格网模型转换至CGCS2000,并与已知的CGCS2000坐标比较,计算坐标转换标准偏差,结果见表 4。计算表明,我国BJS54到CGCS2000坐标转换格网模型的点位精度约为0.25m,XAS80到CGCS2000坐标转换格网模型的点位精度约为0.03m。相比可见XAS80的局部性误差比BJS54已大大减弱。
| 坐标 转换 | 格网 间距 | 公共 点数 | 外检 点数 | 中误差/m | 点位误差 /m | |
| B分量 | L分量 | |||||
| BJS54 → CGCS2000 | 2.5′×2.5′ | 48 433 | 484 | 0.124 | 0.259 | 0.259 |
| XAS80 → CGCS2000 | 2.5′×2.5′ | 48 433 | 484 | 0.017 | 0.028 | 0.028 |
全国性坐标转换格网模型不一定能满足城市区域性测绘工作的应用需求,例如:分米级精度的格网模型不能满足1∶1000地形图的坐标转换精度要求。我国还有十多万个直接用于控制测图的国家低等级控制网点和城市独立坐标系控制网点,这些点尚无CGCS2000成果,地方测绘部门通过区域网联合平差或GPS测量可以获得它们的CGCS2000坐标。公共点数量和密度的增加可以构建格网间距更密、精度更高的坐标转换格网模型。
从谱分析的观点来看,当对一个函数进行分格网取平均,则对该函数在一定程度上作了平滑,即对观测值进行了高频滤波。较大格网面积的数据意味着坐标差数据场的分辨率较低,这必然造成所确定的坐标差高频部分的丢失。区域性格网模型的构建将提高全国性格网模型在该区域的分辨率和精度。
根据区域内新增公共点构建区域格网的方法,采用文献[22]提出的拟合推估两步极小解法,第1步由全国格网点内插新增公共点上的拟合值,第2步由各公共点的剩余误差拟合协方差函数,再用拟合推估法构建区域格网。于是,区域格网节点的坐标改正量由两部分组成,一是全国性格网内插得到的量,二是残差改正量。地图数据库中的要素坐标使用区域格网模型转换得到的结果将与低等级控制点平差值的精度相匹配,相当于将地图坐标也进行了重新平差。
计算试验采用某区域(范围8°×12°)805个具有BJS54和WGS84(视为CGCS2000)坐标的公共点数据进行。均匀选取269个点视为国家等级点,模拟计算全国性格网。剩下的536个点视为城市控制点。536点中再均匀提取27个点作为外部检核点,剩下的509点进行区域格网模拟计算,具体方案如下:
试验1(全国格网模拟计算):用269个点建立0.3°的父格网,内插27个外部检核点,统计转换精度。试验2(区域格网模拟计算):在试验1的基础上,以509个点按拟合推估两步极小解法建立0.1°的区域格网,由区域格网内插27个外部检核点,统计转换精度。
计算中,协方差函数采用Reilly函数
式中,A为待定常数;σ2(0)为观测值方差,认为噪声Δ=0,则σ2(0)等于各点残差的平方和均值;σ(d)为两点间的协方差;d为两点间的距离。假如区域格网节点g周围有n个数据点,则该点的协方差推估方程为
根据周围数据点的残差值vi(i=1,2,…,n)便可推估出区域格网节点g的残差值vg。
试算结果见表 5。由表可见,区域格网不仅提高了全国格网的分辨率,也提高了转换精度。由于本算例采用的是同一控制网的数据,数据间的内洽性较好,故对转换精度的提高不太明显。实际应用中,由于城市控制网与国家控制网是分别布设和计算的,故存在区域性系统偏差,其将体现在区域格网模型中,从而较好地提高转换精度。
|
| 试验1 | -0.122 | -0.093 | 0.059 | 0.029 | 0.283 | 0.146 |
| 试验2 | -0.045 | -0.029 | 0.049 | 0.027 | 0.176 | 0.068 |
目前我国已建立了2.5′×2.5′的全国范围格网模型[23, 24],对于有更高转换精度要求的城市地区可在此基础上按上述方法加密区域格网。区域格网数据集作为全国格网的子集存储在各地分布式数据库中,如果应用范围位于区域格网内,则可根据精度要求调用该区域格网模型。
6 结 论(1) 我国BJS54、XAS80坐标系成果向CGCS2000的转换,按不同用户需求分为高、中、低精度3类,其中,高精度转换模型的转换精度为分米级,采用数学模型与数字模型相结合的格网模型构建。格网模型可以拟合大地控制网建立时的各种误差,满足制图等高精度转换的应用需求。
(2) 以最小曲率法构建格网模型,可以同时具备整体光滑和局部光滑特性,更好地符合地图线状要素坐标转换时的连续光滑性。
(3) 格网节点最小曲率法迭代计算,先要通过试验确定最优格网间距,然后依次细化粗格网直到最优格网。格网模型的数据结构可简化为一维向量序列组,按分块层次结构建立空间索引。格网模型可采用多级格网结构,不同级格网间距不同,格网越小,所表达的连续坐标分量差值的分辨率越高。
(4) 全国范围CGCS2000坐标转换最优格网间距为2.5′×2.5′。按48433个2000国家大地控制网点坐标构建了BJS54和XAS80到CGCS2000坐标转换格网模型,转换后的点位精度分别为0.26m和0.03m,已应用于全国1∶25万和1∶5万地形图更新生产。
(5) 在全国格网模型的基础上,根据各城市公共点的密度情况构建区域格网,以提高格网模型的分辨率,获得优于分米级的转换精度,满足1∶1000以上比例尺地形图的坐标转换精度要求。区域格网以全国格网为基础采用拟合推估两步极小法构建。
| [1] | CHEN Junyong. Chinese Modern Geodetic Datum:Chinese Geodetic Coordinate System 2000 and Its Frame[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(3):269-271. (陈俊勇. 中国现代大地基准:中国大地坐标系统2000及其框架[J]. 测绘学报,2008,37(3):269-271.) |
| [2] | YANG Yuanxi. Chinese Geodetic Coordinate System 2000[J]. Chinese Science Bulletin, 2009, 54(9): 2714-2721.(杨元喜. 2000 中国大地坐标系[J].科学通报,2009,54(16):2271-2276.) |
| [3] | WEI Ziqing. Proposal Concerning China Geodetic Coordinate System 2000[J]. Journal of Geodesy and Geodynamics, 2006, 26(2):1-4.(魏子卿. 关于2000中国大地坐标系的建议[J].大地测量与地球动力学, 2006, 26(2):1-4.) |
| [4] | CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS 80 and WGS 84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3):189-194.(程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J]. 测绘学报, 2009, 38(3):189-194.) |
| [5] | SCHWARZ C.North American Datum of 1983[R]. Rockville:National Geodetic Information Center, 1989:256. |
| [6] | DEWHURST W T. NADCON-The Application of Minimum Curvature Derived Surfaces in the Transformation of Positional Data from the North American Datum of 1927 to the North American Datum of 1983[R]. Rockville:NOAA Technical Memorandum, 1990:30. |
| [7] | TOBITA M. Coordinate Transformation Software “TKY2JGD” from Tokyo Datum to a Geocentric Reference System, Japanese Geodetic Datum 2000[J]. Times of Geographical Survey Institute, 2001, 97: 31-57. |
| [8] | OFFICE of the Surveyor-General. Standard for New Zealand Geodetic Datum 2000[S]. Wellington: Land Information New Zealand, 2007. |
| [9] | Intergovernmental Committee on Surveying and Mapping. Geocentric Datum of Australia Technical Manual Version 2.2[EB/OL].[2002-02-13].www.anzlic.org.au/icsm/gdatm/ |
| [10] | JUNKINS D R. Transforming to NAD83[R]. Ottawa:Canada Centre for Surveying, 1998. |
| [11] | LIU Jingnan, SHE Binbin. The Transformation Models for Combining Different Types of 3-D Positioning Network[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1990, 15(2):48-57.(刘经南, 佘彬彬. 不同类三维空间定位网联合处理的坐标转换模型[J]. 武汉测绘科技大学学报, 1990, 15(2):48-57.) |
| [12] | LU Zhiping, ZHU Huatong. The Testing and Unified Expression of Coordinate Transformation Models[J]. Acta Geodaetica et Cartographica Sinica, 1993, 22(3):161-168. (吕志平, 朱华统. 坐标转换模型的检验及统一表示[J].测绘学报, 1993, 22(3):161-168.) |
| [13] | LU Zhiping, XU Dongzhou, ZHU Huatong, et al. The Divide Minimum Method in Geocentric Coordinate Transformation[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(4):275-282.(吕志平, 许东周, 朱华统, 等. 地心坐标转换的分极小法[J]. 测绘学报, 1995, 24(4):275-282.) |
| [14] | CHENG Pengfei, CHENG Yingyan, WEN Hanjiang,et al. Practical Manual of CGCS2000[M].Beijing: Surveying and Mapping Press, 2008. (程鹏飞, 成英燕, 文汉江,等. 2000国家大地坐标系实用宝典[M]. 北京: 测绘出版社, 2008.) |
| [15] | SHEN Yunzhong, HU Leiming, LI Bofeng. Ill-posed Problem in Determination of Coordinate Transformation Parameters with Small Area’s Data Based on Bursa Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2):95-98. (沈云中,胡雷鸣,李博峰. Bursa模型用于局部区域坐标变换的病态问题及其解法[J]. 测绘学报, 2006, 35(2):95-98.) |
| [16] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(5):715-722. (陈义,陆珏. 以三维坐标转换为例解算稳健总体二乘方法[J]. 测绘学报, 2012, 41(5):715-722.) |
| [17] | YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650.(杨元喜.卫星导航的不确定性、不确定度与精度若干注记[J]测绘学报, 2012, 41(5):646-650.) |
| [18] | GUO Chong, LU Zhiping, XU Jigang. Comparison and Analysis of Application of Several Models in Grid Transformation[J]. Bulletin of Surveying and Mapping, 2009(5): 38-41.(郭充, 吕志平, 徐基刚. 几种模型在格网坐标转换应用中的比较与分析[J].测绘通报, 2009(5): 38-41.) |
| [19] | BRIGGS I C. Madrine Contouring Using Minimum Curvature[J]. Geophysics, 1974, 39(1) :39-48. |
| [20] | SMITH W H F,WESSEL P. Gridding with Continuous Curvature Splines in Tension[J]. Geophysics, 1990, 55(3): 293-305. |
| [21] | CHEN Junyong, YANG Yuanxi, WANG Ming, et al. Establishment of 2000 National Geodetic Control Network of China and It’s Technological Progress[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 1-8.(陈俊勇,杨元喜,王敏,等.2000国家大地控制网的构建和它的技术进步[J].测绘学报, 2007, 36(1): 1-8.) |
| [22] | YANG Yuanxi, LIU Nian. A New Resolution of Collocation by Two Minimization Steps[J]. Acta Geodaetica et Cartographica Sinica, 2002,31(3):192-195.(杨元喜,刘念. 拟合推估两步极小解法[J].测绘学报, 2002, 31(3):192-195.) |
| [23] | LU Zhiping, LI Jian, ZHANG Xiguang. China Geodetic Coordinate System 2000 and Its Application[M]. Beijing: PLA Press, 2012.(吕志平, 李健, 张西光. 2000中国大地坐标系及其应用[M]. 北京: 解放军出版社,2012) |
| [24] | YANG Huazhong, LI Jun, WANG Zhouping, et al. The Transformation from Old Coordinate Systems to CGCS2000 in China[J]. Geomatic Science and Engineering, 2007,27(4):1-6. (杨华忠, 李军, 汪舟平, 等. 我国常用大地坐标系与2000中国大地坐标系间的转换[J].测绘科学与工程, 2007, 27(4):1-6.) |