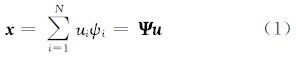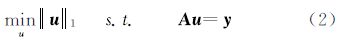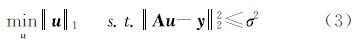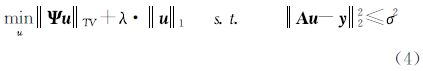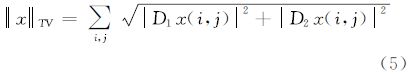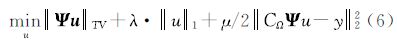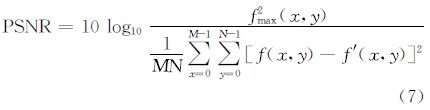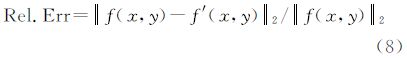1 引 言
随着航空地磁测量精度的提高以及高精度插值算法的应用,地磁数据的网格分辨率达到百米量级左右,大大提高了数据的空间分辨率,其丰富的纹理信息,更利于应用地磁及其梯度数据进行辅助导航[1, 2, 3, 4, 5]。但由于数据量的剧增,对导航数据库构建提出了较高的要求,研究大容量地磁数据的压缩方法,降低高分辨率数据库的存储容量具有重要意义。
传统数据压缩方法是以牺牲数据的高频细节信息为代价,通常运用BDCT(blocking discrete cosine transform)编解码技术对数据进行分块变换处理[6]。较大分块数据相关性较高,可以实现较大的压缩比,但大尺寸分块数据压缩时又会丢失数据的平稳性,引入振铃效应(ringing effect)噪声和块效应(block effect)边界误差[7, 8, 9]。由此重构的数据高频轮廓特征信息损失严重或引入重构噪声,增大了地磁辅助导航系统匹配失败或是误匹配的概率[10, 11],因此不适用于大容量的导航数据压缩。
压缩感知(compressed sensing,CS)作为一种新兴的稀疏信号精确重构理论已成为核磁共振和合成孔径雷达成像等图像处理领域的重要方法[12, 13]。由于地磁数据能量多集中在低频分量上,而压缩感知对稀疏信号的随机采样矩阵通常为局部傅里叶变换系数星形采样,这种采样矩阵破坏了低频分量系数之间的相关性,影响了数据重构精度[14, 15]。
为解决大容量地磁数据压缩的同时,又能较好地保存细节轮廓信息的问题,本文提出一种基于压缩感知理论的数据分频压缩及联合重构方法。
2 压缩感知理论压缩感知是一种新兴理论,它根据信号本身或在变换域中具有的稀疏特性,利用远少于Nyquist采样定理所需的采样数据就可以精确地重构原始数据,因此,该理论在各个领域中展开广泛研究及应用[16]。
假设离散信号x∈RN在小波变换下的稀疏度为K,则原始信号可用一组小波变换的稀疏基Ψ={ψi}i=1N线性表示为
根据压缩感知理论,当随机测量矩阵Φ与稀疏变换矩阵Ψ满足约束等距性(restricted isometry property,RIP)条件,即可利用信号x线性测量获得的观测值y=Φx=Au,通过解决以下l1范数最小值问题来实现原始数据的精确重构
式中,A=ΦΨ为感知矩阵,当线性测量值含有高斯噪声时,根据噪声大小σ对上式中l1范数约束条件适当松弛,寻找l1范数最小值问题可以表述为以下线性凸优化问题l1范数定义为||w||1=∑i|wi|,最小化||u||1保证求解的稀疏性,约束||Au-y||22≤σ2使求解与最优解具有一致性,式(3)是在稀疏变换域Ψ中寻找最优稀疏解。
对于时域中绝大多数图像数据,其离散梯度具有稀疏性,全变差(total variation,TV)正则化模型能够比较合理地保持图像的轮廓结构和边缘特征[17]。因此,全变差方法常作为稀疏变换,替代l1范数应用在压缩感知方法中[12]。文献[18, 19]结合TV正则化和l1范数的优点,给出同时在稀疏变换域以及稀疏梯度时域中寻找最优解的压缩感知模型
式中,规划参数λ≥0,选择适当的λ可以调整稀疏变换域中l1范数和时域全变差两种方法在凸优化寻求最优解过程中所占的比重。对于图像数据x,其全变差定义为 式中,D1x=x(i+1,j)-x(i,j),D2x=x(i,j+1)-x(i,j)为图像的像素点x(i,j)在水平和垂直方向上的有限差分。由于TV正则化和l1范数都具有非平滑、不可微分的特性,传统优化算法如共轭梯度法和匹配追踪算法在解决以上优化问题时,需要耗费大量的计算时间[20, 21]。近期一些快速算法如TwIST、FISTA、TVAL3和RecPF等的出现,使得在求解压缩感知问题时可以节省大量的时间[22, 23, 24, 25]。
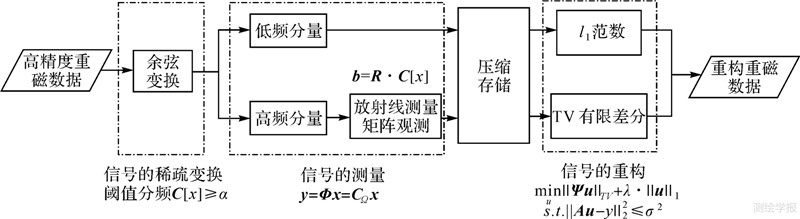
3 基于压缩感知的分频压缩及重构方法对于导航用地磁数据,压缩时需要保留精度较高的边缘、轮廓和纹理等局部高频特征,基于压缩感知理论的数据分频压缩及联合重构方法主要包含两部分内容:频域余弦变换的分频压缩和基于压缩感知的联合重构。
分频压缩方法的主要过程为:
(1) 以较大范围的高精度地磁数据作为整体进行二维离散余弦变换,以将数据进行多尺度频率分解。
(2) 设置变换域系数阈值α,将幅值大于阈值的低频分量系数进行无损编码。
(3) 高频分量系数包含边缘和纹理成分,利用放射线采样矩阵R对高频分量系数进行稀疏采样编码。
数据重构方法的主要过程为:
(1) 对分频压缩存储的低频系数和高频系数按所处位置进行重组,作为压缩感知重构中的线性观测值y=Φx。其中,测量矩阵Φ为局部余弦变换系数矩阵Φ=CΩ=Ω′·C[·],C[·]代表二维离散余弦变换,随机采样矩阵Ω′既包含对高频分量系数的随机放射线采样,又含有对大于阈值的低频系数的确定性采样。 (2) 将上述局部余弦变换系数作为观测采样值,通过求解式(4)在小波稀疏变换域中l1范数最小化以及时域全变差正则化的问题重构原始地磁数据。
实现数据分频压缩与重构方法的部分伪码如下:
步骤1:加载地磁异常数据x,对数据进行归一化处理,设置二维网格数据的间距为Δx、Δy,网格数为m、n参数。
步骤2:进行余弦变换系数分频。对整体地磁数据进行离散余弦变换u=DCT(x),设置分频系数阈值参数α,将变换域系数分解为高频和低频系数。
步骤3:局部余弦变换系数采样压缩。对低频系数进行无损压缩编码u′L=uL,利用放射线采样矩阵R对高频系数进行稀疏采样压缩编码u′H=R·uH。
步骤4:获得重构的线性观测采样数据。对压缩编码系数解码,根据采样位置生成局部余弦变换测量观测值y=CΩ·x。
步骤5:公式(4)可转换为拉格朗日无约束项形式的TVL1-L2压缩感知模型公式
步骤6:根据公式(6),利用文献[25]提出的RecPF算法求解TV正则化和l1范数最小化的优化问题,最终获得压缩重构的地磁数据。该方法基于经典的带参数拉格朗日算法,利用方向选择算法实现优化问题的快速计算,在每次迭代过程中仅包含局部余弦变换系数阈值计算,迭代次数更少,抗差性更强。
通过步骤1~3实现了分频压缩,对大多数地磁数据而言,高频分量可近似认为是稀疏的,但低频分量不是稀疏的,它是数据主要能量在较低频率下的逼近信号。如果将高、低频系数一起与放射线采样矩阵R相乘,则在较低采样率的情况下会破坏低频分量系数之间的相关性,导致重构效果变差。另外由于低频系数所占的比重很小,约3%左右,因此完整保留这些少量的含有重要信息的系数不会影响到数据的压缩效率,反而由于精确地保留了这些系数,可以有效提高重构数据的质量。
而采用步骤4~6利用压缩感知方法精确重构地磁数据。该方法不仅在小波变换域中严格稀疏,而且在时域具有较小的全变差,有效地解决了数据平滑与轮廓维持之间的矛盾,在优化重构过程中抑制高频误差噪声的同时不对最优解加强平滑作用,较好地保留了地磁数据的轮廓和纹理特征,减少了重构中的高频误差。算法结构框图如图 1所示。
|
| 图 1 基于压缩感知的数据分频压缩及重构算法结构框图 Fig. 1 The block diagram of data frequency divisive compression and reconstruction algorithm based on compressed sensing |
美国国家地球物理数据中心(NGDC)网站提供反映当地区域内磁场高频分量的地磁异常磁数据。以2002年发布的美国加州地区某处航磁测量数据作为本文仿真试验数据,机载磁力仪精度为1 nT,数据采样频率为2 Hz,地磁异常数据已消除了地磁场的日变影响,误差在2 nT以下或更低。对航磁测线数据经过Kriging插值、滤波处理形成了100像素×100像素网格数据,如图 2(a)所示,数据经度范围:-122.04°~-121.9°,纬度范围:36.20°~36.34°,分辨率为5″,地磁异常数据统计特征如表 1中所示。

|
| 图 2 原始地磁异常数据及余弦变换局部系数采样模式 Fig. 2 The original geomagnetic anomaly data and DCT domain sampling pattern |
| nT | ||||
| 特征参数 | 最大值 | 最小值 | 平均值 | 标准差 |
| 852.72 | 47.75 | 508.59 | 66.33 | |
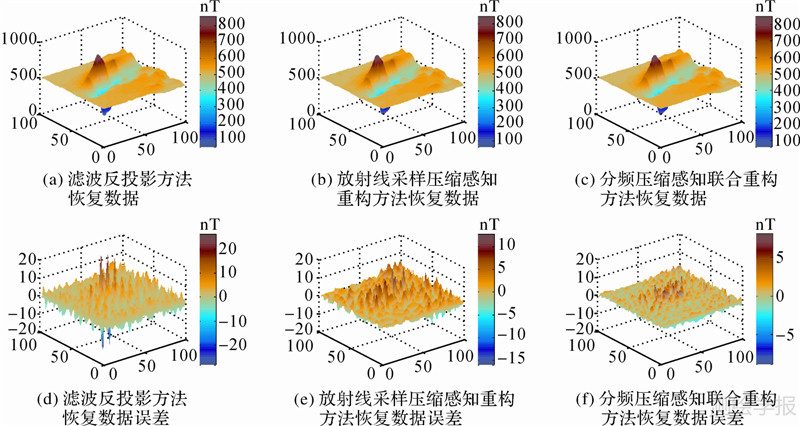
为分析重构数据精度,以及压缩感知和分频压缩在数据重构中独立发挥的作用,另外给出两个压缩重构方法进行对比:一个为滤波反投影方法(filtered back projection);另一个为直接放射线采样方法,即对余弦变换系数不进行分频采样压缩,并同样利用压缩感知方法来重构地磁异常数据。
首先对地磁异常数据归一化处理并进行离散余弦变换,由于离散余弦变换具有频率分解和能量压缩的特性,使得数据在变换域中较大的系数集中在图像的左上角,本文方法通过设置离散余弦变换阈值参数α,将地磁数据在频域中分为低频和高频分量。本仿真试验中根据实际情况取α=0.5,则余弦变换低频分量系数采样率为2.45%,如图 2(b)所示。然后对高频分量系数进行随机采样,采样系数为28条放射线测量,如图 2(c)所示。将以上获得分频压缩总采样率为25%的采样系数作为本文方法及滤波反投影方法的重构观测数据。同时利用放射线直接采样获得同样总采样率的系数作为直接放射线采样方法重构观测数据。表 2给出不同采样方法高频和低频系数所占比例。
| 重构方法 | 总采样率/(%) | 低频采样率/(%) | 高频采样率/(%) | PNSR/dB | ΔPNSR/dB | 相对误差/(%) | 重构时间/s |
| 滤波反投影 | 25 | 2.45 | 22.55 | 47.79 | -- | 0.54 | 0.1 |
| 放射线采样 | 25 | 2.07 | 22.93 | 49.63 | 1.84 | 0.44 | 1.6854 |
| 分频压缩 | 25 | 2.45 | 22.55 | 52.60 | 4.81 | 0.25 | 1.6925 |
利用图像质量客观评价标准:峰值信噪比和相对误差对复原数据结果进行评价。峰值信噪比定义如下
相对误差定义为 式中,fmax(x,y)为地磁异常数据最大值;f(x,y)为原始数据;f′(x,y)为待评价重构数据;M、N为数据网格数;‖·‖2为l2范数。图 3中(a)~(f)为总采样率均为25%时,3种压缩重构方法恢复地磁数据以及相对于原始数据误差。表 2给出3种重构方法恢复数据的峰值信噪比和相对误差统计结果。可以看出,虽然滤波反投影重构方法与分频压缩方法为相同的观测重构系数,但在重构算法中利用压缩感知能更精确地重构高频分量数据,峰值信噪比提高了4.81 dB。而与放射线采样方法相比,分频压缩方法通过阈值采样,在较低采样率下保留更多的低频分量系数,重构数据中含有更精确的低频分量数据信息,峰值信噪比相对放射线采样方法提高了2.97 dB。从重构算法的计算时间来看,本文方法需要求解l1范数最小化和TV正则化等凸优化问题,虽然计算时间比滤波反投影重构方法长,但在可允许的计算时间内提高重构数据精度是值得的。
|
| 图 3 采样率为25%时3种重构方法恢复数据结果 Fig. 3 The retrieval results of three different algorithms with sampling ratio 25% |
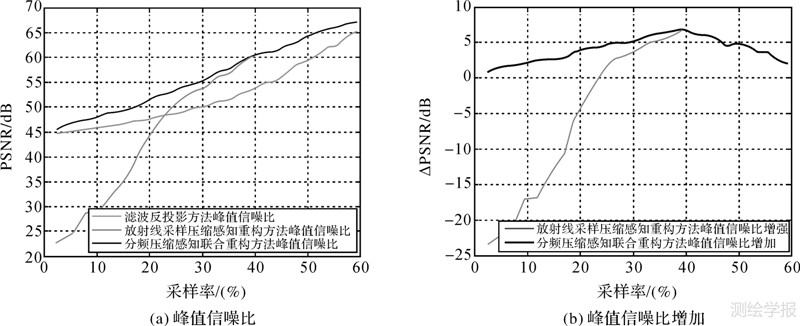
离散余弦变换阈值参数α的设置决定了在数据压缩中低频分量的采样率,而放射线采样矩阵R决定高频分量的采样率,为分析不同采样率对3种方法重构数据的峰值信噪比影响,图 4给出各方法在不同采样率下的峰值信噪比,以及相对于滤波反投影重构方法,其他两种方法增加的峰值信噪比。通过分析可以得出以下两点结论:
|
| 图 4 不同数据采样率下重构算法峰值信噪比分析 Fig. 4 Analysis of reconstruction algorithms’ PSNR via different sampling ratios |
(1) 基于压缩感知的分频压缩方法在不同采样率下重构数据均具有更高的峰值信噪比,与传统滤波反投影方法相比可分别增加1~6 dB左右。表明将压缩感知方法应用于高压缩比的地磁数据压缩重构中具有明显的优势。
(2) 由于采用余弦变换阈值进行分频压缩,有效保留了低频分量数据,可以避免如放射线采样方法在采样率小于23%时,峰值信噪比低于滤波反投影重构方法的情况,表明本文方法在较低采样率条件下仍能保证较高的重构精度。随着采样率增加,放射线采样方法逐渐包含更多重要的低频分量系数,重构精度增加,在采样率大于40%以后精度与本文方法相同。
5 结 论地磁辅助导航系统中需存储大量高精度地磁数据作为基准图数据库。针对传统数据压缩方法存在高频细节信息损失严重的问题,提出基于压缩感知理论的分频压缩联合重构方法,在余弦变换压缩编码过程中不对其低频变换系数压缩使之处于特殊的地位,而对高频变换系数进行稀疏采样压缩编码,实现数据压缩。这样不仅能较完整地保存低频分量数据,同时利用压缩感知重构算法,优化了重构方法中的随机观测矩阵,可以精确重构原始数据中高频分量特征,因此重构数据不会像滤波方法使整个数据图像平滑,而是保留清晰的轮廓,从而在较高数据压缩比条件下获得更高质量的重构数据。
| [1] | HEMANT K, THÉBAULT E, MANDEA M, et al. Magnetic Anomaly Map of the World: Merging Satellite, Airborne, Marine and Ground-based Magnetic Data Sets[J]. Earth and Planetary Science Letters, 2007, 260(1-2): 56-71. |
| [2] | NABIGHIAN M N, GRAUCH V J S, HANSEN R O, et al. The Historical Development of the Magnetic Method in Exploration[J]. Geophysics, 2005, 70(6): 33N-61N. |
| [3] | ZHOU Jun, GE Zhilei, SHI Guiguo, et al. Key Technique and Development for Geomagnetic Navigation[J]. Journal of Astronautics, 2008, 29(5): 1467-1472. (周军,葛致磊,施桂国,等. 地磁导航发展与关键技术[J]. 宇航学报, 2008, 29(5): 1467-1472.) |
| [4] | QIAN Dong, LIU Fanming, LI Yan, et al. Comparison of Gravity Gradient Reference Map Composition for Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 736-744. (钱东,刘繁明,李艳,等. 导航用重力梯度基准图构建方法的比较研究[J]. 测绘学报, 2011, 40(6): 736-744.) |
| [5] | WANG Shicheng, WANG Zhe, ZHANG Jinsheng, et al. Technology of Preparation of Reference Map Using Total Geomagnetic Intensity Gradient Module[J]. Systems Engineering and Electronics,2009, 31(4): 881-885. (王仕成,王哲,张金生,等. 总磁场强度梯度模作为匹配特征量的基准图制备技术[J]. 系统工程与电子技术, 2009, 31(4): 881-885.) |
| [6] | RAO K R, YIP P. Discrete Cosine Transform: Algorithms, Advantages, Applications[M]. Waltham:Academic Press, 1990. |
| [7] | KASEZAWA T. Blocking Artifacts Reduction Using Discrete Cosine Transform[J]. IEEE Transactions on Consumer Electronics,1997, 43(1): 48-55. |
| [8] | XU Jinbo. An Improved Algorithm to Remove the Block Effect in Transform Encoder Images[J]. Computer Engineering and Science,2006, 28(2): 51-53. (徐金波. 变换编码中消除图像“块效应”的优化算法[J]. 计算机工程与科学,2006, 28(2): 51-53.) |
| [9] | ZOU J J, YAN H. A Deblocking Method for BDCT Compressed Images Based on Adaptive Projections[J]. IEEE Transactions on Circuits and Systems for Video Technology,2005, 15(3): 430-435. |
| [10] | LUO S, WANG Y, LIU Y, et al. Geomagnetic- Matching Technology Based on Improved ICP Algorithm[J]. Journal of Computer Applications, 2008(s1): 351-354. |
| [11] | WANG Xianglei. The Study of Some Key Technology in Geomagnetic Matching Navigation[J]. Engineering of Surveying and Mapping, 2011, 20(1): 1-5. (王向磊. 地磁匹配导航中几项关键技术研究[J]. 测绘工程, 2011, 20(1): 1-5.) |
| [12] | CANDÉS E J, ROMBERG J, TAO T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. |
| [13] | PATEL V M, EASLEY G R, HEALY J D M, et al. Compressed Synthetic Aperture Radar[J]. IEEE Journal on Selected Topics in Signal Processing, 2010, 4(2): 244-254. |
| [14] | CANDES E J, TAO T. Near-optimal Signal Recovery from Random Projections: Universal Encoding Strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425. |
| [15] | PATEL V M, MALEH R, GILBERT A C, et al. Gradient-based Image Recovery Methods from Incomplete Fourier Measurements[J]. IEEE Transactions on Image Processing, 2012, 21(1): 94-105. |
| [16] | TROPP J A, LASKA J N, DUARTE M F, et al. Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals[J]. IEEE Transactions on Information Theory,2010, 56(1): 520-544. |
| [17] | RUDIN L I, OSHER S, FATEMI E. Nonlinear Total Variation Based Noise Removal Algorithms[J]. Physica D: Nonlinear Phenome- na, 1992, 60(1-4): 259-268. |
| [18] | CANDÉS E J, ROMBERG J K. Signal Recovery from Random Projections[C]//Proceedings of SPIE. San Jose: [s.n.], 2005. |
| [19] | CANDÉS E, BRAUN N, WAKIN M. Sparse Signal and Image Recovery from Compressive Samples[C]// Proceedings of International Symposium on Biomedical Imaging: From Nano to Macro. Arlington: [s.n.], 2007. |
| [20] | LUSTIG M, DONOHO D, PAULY J M. Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging[J]. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195. |
| [21] | TROPP J A. Greed is Good: Algorithmic Results for Sparse Approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. |
| [22] | BIOUCAS-DIAS J M, FIGUEIREDO M A T. A New TwIST: Two-step Iterative Shrinkage/Thresholding Algorithms for Image Restoration[J]. IEEE Transactions on Image Processing, 2007, 16(12): 2992-3004. |
| [23] | BECK A, TEBOULLE M. Fast Gradient-based Algorithms for Constrained Total Variation Image Denoising and Deblurring Problems[J]. IEEE Transactions on Image Processing, 2009, 18(11): 2419-2434. |
| [24] | ZUO W, LIN Z. A Generalized Accelerated Proximal Gradient Approach for Total-Variation-Based Image Restoration[J]. IEEE Transactions on Image Processing, 2011, 20(10): 2748-2759. |
| [25] | YANG J, ZHANG Y, YIN W. A Fast Alternating Direction Method for TVL1-L2 Signal Reconstruction from Partial Fourier Data[J]. IEEE Journal on Selected Topics in Signal Processing,2010, 4(2): 288-297. |