影像匹配是指通过一定的匹配算法在两幅或多幅影像之间识别同名点的过程,它是图像处理及计算机视觉领域中的一个非常重要的热点问题[1]。所以,稳定、精确、快速的影像匹配算法有利于进行对图像信息的后续处理的研究。影像匹配方法大致分为两类:基于影像灰度的匹配[2]与基于特征的匹配[3]。SIFT算法[4]是由文献[5—6]提出的一种提取局部特征的方法[7],由于利用了图像中数量较少、特征较稳定的一些点、线或边缘等进行匹配,大大压缩了所需处理信息量,使得匹配搜索的计算量小,速度较快。而且该方法对图像灰度的变化具有鲁棒性,是目前研究最多、应用最广的一类匹配方法。SIFT算法通过在尺度空间探测极值,提取具有稳健性的特征描述向量[4]。在传统SIFT算法的基础上,本文提出了一些改进的SIFT算法。为了综合利用影像的结构特征和灰度特征,文献[8]中提出了基于SIFT特征和灰度特征的综合匹配相似性测度的计算方法。考虑到在图像发生旋转后,特征点周围的区域都会发生变化,而圆具有很好的旋转不变性,文献[9]中提出可以用圆来构造 SIFT 特征点描述符,在以特征点为中心的圆形区域内构造4个圆环,在每个圆环内分别计算(0°,360°)均匀分布的 12 个方向上的梯度直方图。针对匹配中存在的重复匹配和多对一匹配等问题,文献[10]优化了其关键点匹配策略,通过比较匹配点对的像素坐标值和遍历对应点对的索引值将其全部提取出来,这就提高了匹配点对的精确度。
传统RANSAC在假设检验时采用的是随机抽样,即认为每个点的正确点先验概率是相同的,这在有很多粗差点存在时会增加迭代次数,严重地影响运算效率。为提高运算效率,本文引入了基于贝叶斯抽样一致性的BAYSAC算法[11]。该算法在每次假设检验时总是选择正确点概率最高的点,能有效地减少找到最优模型所需的迭代次数和运算时间,提高匹配的效率。本文在原有BAYSAC算法基础上,对正确点先验概率确定和概率更新两部分进行了优化。
2 基于SIFT特征匹配的BAYSAC算法SIFT算法是基于特征的匹配方法,它的匹配能力很强,但受各种外部噪声因素的影响,要准确地对特征点进行无歧义的匹配难度很大,通常会在一定程度上引起特征的误匹配。因此,影像匹配中通过实现模型参数的稳健性估计剔除误匹配。传统的模型参数的稳健性估计方法,例如RANSAC算法,已经在图像匹配的领域取得了良好的效果。BAYSAC算法以RANSAC算法的原理为基础,结合了贝叶斯估计的原理,能有效剔除影像匹配粗差点,得到精确可靠的匹配结果,提高SIFT算法的稳健性。
2.1 SIFT算法简介SIFT (尺度不变特征变换:scale invariant feature transform)算法由D. G. Lowe在1999年所发表,2004年完善总结。它通过在尺度空间探测极值,提取具有稳健性的特征描述向量。SIFT特征匹配算法的匹配能力很强,它能够处理两幅影像之间发生平移、旋转、仿射变换情况下的匹配问题,寻找匹配最佳点位。
SIFT特征匹配的主要步骤如下[12]:
① 建立尺度空间;② 尺度空间极值探测;③ 确定特征点方向;④ 提取SIFT区域特征描述向量;⑤ 寻找最佳匹配点位。
2.2 RANSAC算法RANSAC(random sample consensus)算法,也称作随机抽样一致性算法,它是一种稳健性的算法,最早于1981年由文献[13]提出。与M-estimator[14]、L-estimator[15]和LMedS[16]等统计方法类似,该算法广泛运用在计算机视觉的各领域,成为估计基本矩阵的基本方法之一。RANSAC算法估计基本矩阵时,要求在置信概率为p的条件下,在预匹配的特征点集组中随机抽样n次,每次抽样的数据量为m,要保证至少有一次抽样的数据全是正确点[17]。传统的RANSAC算法为剔除影像误匹配提供了有效的途径,它尽可能地剔除了粗差点,一定程度地提高了影像匹配的稳健性。
2.3 BAYSAC算法 2.3.1 算法原理BAYSAC(Bayes sample consensus)算法是指贝叶斯抽样一致性,由文献[11]提出。传统RANSAC方法下由随机产生的假设点集估计基本矩阵模型,并选择符合点数最多的模型作为最佳模型。BAYSAC算法则是利用可能拥有的每个点的正确点可能性(概率)作为先验信息,在每次抽样时总选择具有最高先验概率的n个点作为假设点集计算模型参数,用模型符合点数判断该模型是否是更好的模型;之后结合贝叶斯公式更新每个样本点的正确点概率,作为下次假设检验时的正确点先验概率,进入下一次抽样。BAYSAC算法在每次抽样时总选择正确点概率最高的n个点作为假设点集,能够减少得到最佳模型所用的时间,提高计算效率。
本文引入了原始BAYSAC算法基于随机概率的先验概率确定方法,并对原始BAYSAC算法进行改进,主要体现在:① 结合影像对的几何成像原理确定几何约束以确定先验概率;② 对概率更新公式进行优化,用检验模型最优的概率来估计假设点集整体为局内点最优的可能性,并用k/D作为检验模型是否最优的评价指标。 2.3.2算法步骤
(1) 由如下公式获得欲抽样的次数T
式中,p为置信区间;ε为数据集的错误点所占的比率;n为样本容量;(2) 选择数据集合中正确点概率最高的n个点作为假设点集;
(3) 由所选假设点集计算基本矩阵;
(4) 对数据集内剩余的点进行检验,以点到对应核线的距离判断正确点和粗差点,将距离超出阈值的点作为粗差点剔除;
(5) 每次循环结束前更新每个点的正确点概率Pt(i∈I),进入下一次循环;
(6) 重复步骤2—5,直至达到抽样次数T;
(7) 记录符合点数最多的模型,认为该模型为最佳基本矩阵模型;
(8) 用符合最佳基本矩阵模型的点估计最终的模型参数。
BAYSAC算法要解决的核心问题是正确点先验概率的估计,以及每次假设检验之后正确点概率的更新。
2.3.3 正确点先验概率估计方法BAYSAC算法是基于RANSAC算法的改进,体现在以每个点的正确点先验概率作为抽样的依据。然而在实际应用中,正确点先验概率是很难得到的,因此要尽可能准确地估计点的正确点先验概率。本文分析了不同影像的成像特点,确定了3种正确点先验概率的估计方法:
2.3.3.1 基于随机概率U(0,1)的正确点先验概率估计方法这种估计先验概率的算法由文献[11]提出。由于概率值为分布在(0,1)之间的浮点数,因此,选取基于随机概率U(0,1)分布的随机值作为每个点的正确点先验概率。这种方法可通用于不同影像。试验中这种正确点先验概率的估计算法用RANDOM-BAYSAC表示。但由于其概率估计的随机性,很有可能将较大的概率值赋给原本是误匹配的点,导致无法有效剔除误匹配,保留正确匹配。因此本文还结合了不同的影像成像原理,提出了两种正确点先验概率的估计方法。
2.3.3 .2 基于像点到像片中心距离比值的正确点概率估计方法
沿主光轴方向拍摄的地面影像在拍摄时,摄影机是沿主光轴推进的。影像同名点间的几何关系如图 1所示。

|
| 图 1 地面影像坐标几何关系 Fig. 1 Geometric relationships of ground image coordinates |
图 1中S1(S2) 为两个摄站,r1(r2) 为S1(S2)沿基线到像片的距离,ΔS为基线长度,LA(LB)为物方点A(B)到其主光轴上投影点的距离,DA(D′A) 和DB(D′B)是物方点A(B)所在平面与摄站S1(S2) 间的距离,lA(l′A)和lB(l′B)是同名点a(a′)/b(b′)到同名像对中心的距离,取像幅长(宽)的一半作为像片中心的坐标。即可得到如下所示的几何关系
如式(2)所示,对于一对同名像点,像点到两张像片中心的距离与像点到两摄站的距离成反比。像点到两摄站的距离差为基线长度ΔS ,ΔS是一个常量。ΔS 相对于多数D′都是一个较小的值,使得ΔS/D′成为一个较小的量。因此对于不同的同名点对,如式(3)所示,比值l′/l是一个集中在1附近的变量,即一个近似于常量1的变量。用SIFT匹配得到的同名点坐标计算每个点l′/l的值,并统计该比值的分布,计算其在出现峰值的区域内的均值,该均值即被看作是描述两张像片几何关系的比值常量的最近似值。在改进的算法中,以同名像点与像片中心的距离的比值在峰值区域内的均值作为赋予先验概率的参考。若某个点的距离比值偏离这个均值太多,则认为该点是错误匹配的可能性较大,即赋予其较小的先验概率。试验中这种正确点先验概率的估计算法用RATIO-BAYSAC表示。
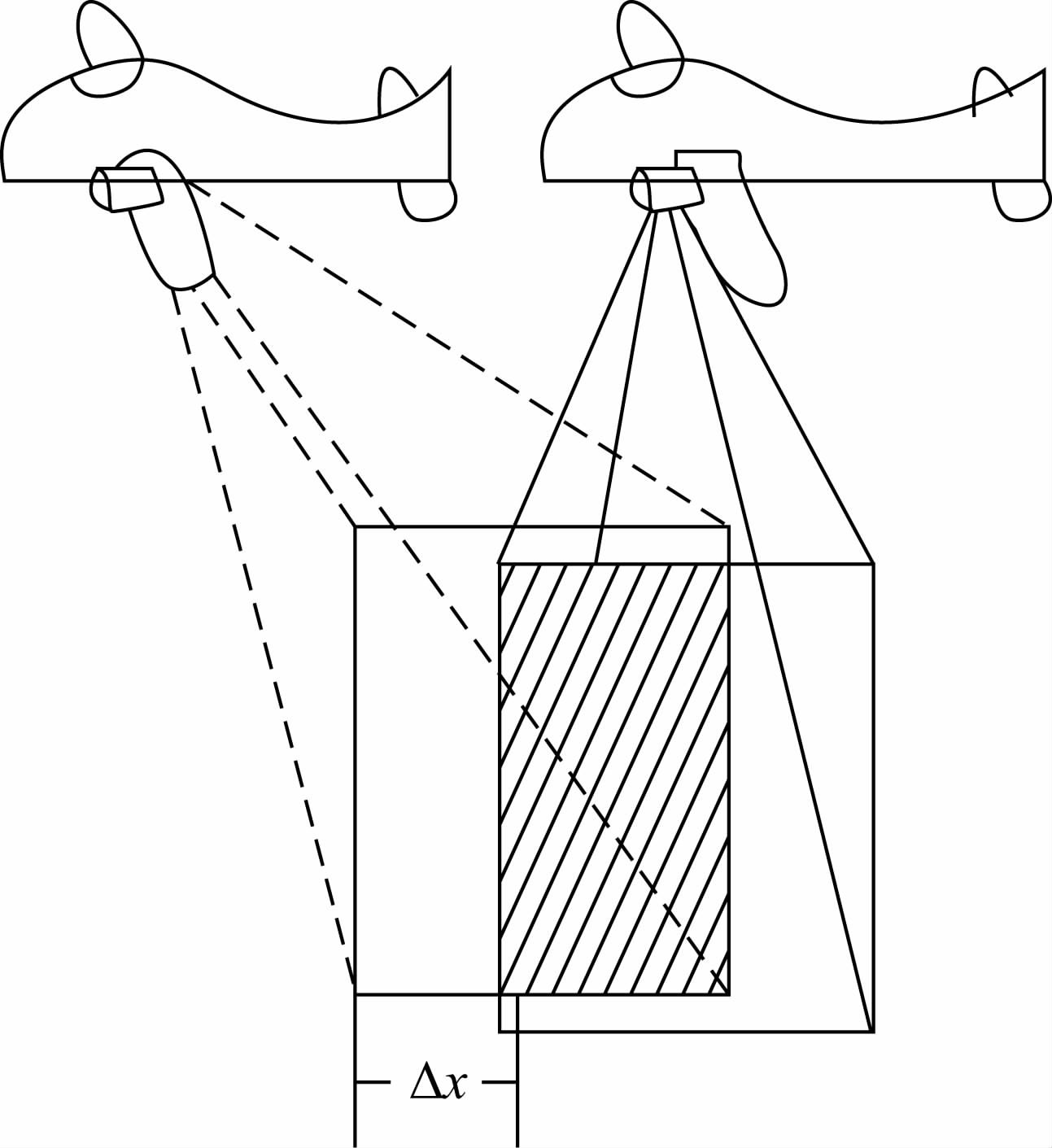
2.3.3 .3 基于影像重叠度的正确点先验概率估计方法航空影像在拍摄时,相邻相片的航向重叠度一般应为60%~65%,最大不大于75%,最小不小于56%[18]。因此在航行基本稳定,航高和航向没有太大的变化时,对于每个物方点,它在两幅图像上对应的视差应该是一个常量,如图 2。
为估计视差的常量,用SIFT匹配得到的同名点坐标计算每个点的视差,并统计该视差的分布,计算其在出现峰值的区域的均值,该均值即被看作是描述两幅相片偏移关系的最近似值。在改进的算法中,以两幅图像对应方向的视差在峰值区域内的均值作为赋予先验概率的参考。若某个点的坐标偏移量偏离这个均值太多,则认为该点是错误匹配的可能性较大,即赋予其较小的先验概率。试验中这种正确点先验概率的估计算法用OVERLAP-BAYSAC表示。
|
| 图 2 航空影像坐标偏移 Fig. 2 Coordinate shift of aerial image |
“嫦娥一号”卫星搭载的三线阵CCD立体相机,在卫星飞行过程中连续获取前视、正视、后视3个线阵的数据,形成3幅连续影像,同一地物在一定的时间内分别被前、正、后视3条线阵扫过[19]。由于相机的前视、正视和后视线阵之间的夹角不大,获取的前视、正视和后视影像两两之间都存在近100%的重叠度[20]。适用于基于影像重叠度的正确点先验概率估计方法。
2.3.4 概率更新公式文献[11]中提出的贝叶斯公式更新正确点先验概率的公式如下
式中,Pt-1i∈I表示更新前的正确点先验概率;Pti∈I表示更新后的正确点先验概率;P(Ht⊄I)表示样本数据中存在粗差点的概率;P(Ht⊄I|i∈I)表示i点为正确点时样本数据中存在粗差点的概率。贝叶斯公式可按照相似性度量的原理进行简化
其中,L(A|B)反映了概率更新前后的相似性。若某次假设检验符合点数较多,则认为其选择的假设点集较优。用每次检验模型最优的概率来估计假设点集整体为局内点最优的可能性,并用此评价检验前后正确点概率的相似性 式中,k为某次假设检验模型的符合点数;D为所有的数据点。即可优化贝叶斯抽样一致性正确点概率更新的公式 3 试 验本文用基于不同成像原理的两组像对的试验结果为例,比较RANSAC算法和BAYSAC算法在剔除误匹配时的表现。其中像对Ⅰ是沿主光轴方向拍摄的地面影像,像对Ⅱ为“嫦娥一号”卫星搭载的三线阵CCD相机推扫的月表影像。
SIFT算法提取匹配点时,当两幅图像的SIFT特征向量生成后,可以用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取出图像A中的某个关键点,并找出其与图像B中欧式距离最近的前两个关键点。获得这两个关键点后,给定一个小于1的数值作为阈值θ,用距离最近的两个关键点点中最近的距离除以次近的距离,若获得的比值少于θ,则接受这一对匹配点。一般情况下,θ取0.6时,能得到稳健的匹配点。提高这个比例阈值,SIFT匹配点数目就会增加,但容易出现误匹配点。为比较RANSAC算法和BAYSAC算法在不同数量的误匹配存在时的表现,分别将SIFT算法的阈值θ设置为0.6和0.8,这样一个像对能得到两组数量不同的同名点,试验数据见表 1。用RANSAC算法和BAYSAC算法对由SIFT算法得到的每幅影像的两组数据分别进行处理,匹配效果见表 2。
| 序号 | θ=0.6 (误匹配点百分比) | θ=0.8 (误匹配点百分比) |
| I | 368(18.2%) | 571(21.5%) |
| II(1) | 839(0.9%) | 903(5.3%) |
| II(2) | 703(3.0%) | 781(10.4%) |
像对I是沿主光轴拍摄的地面影像,影像分辨率为4500像素×3000像素。θ=0.6时由SIFT算法提取的匹配点数为368个(见图 3);θ=0.8时由SIFT算法提取的匹配点数为571个(见图 4)。

|
| 图 3 θ=0.6时SIFT匹配的同名点 Fig. 3 Correspondences extracted by SIFT with the threshold 0.6 |

|
| 图 4 θ=0.8时SIFT匹配的同名点 Fig. 4 Correspondences extracted by SIFT with the threshold 0.8 |
如表 1,当SIFT算法的阈值不同时,提取的同名点有不同的误匹配率。对于像对I,θ=0.6和θ=0.8时的误匹配点率都较大,导致RANSAC运行效率较低;而RANDOM-BAYSAC和RATIO-BAYSAC的运行效率则很高,并能有效剔除粗差点,如图 5。
图 5 (a)、(b)、(c)分别为RANSAC、RANDOM-BAYSAC和RATIO-BAYSAC算法试验结果的细部放大图。图中可以看到,经RATIO-BAYSAC算法处理后,图像右侧边缘(图 5 (c))的错误匹配得到了有效的剔除。

|
| 图 5 像对I匹配细部放大图 Fig. 5 Zoom-in parts of image pair I |
像对Ⅱ(1)是“嫦娥一号”卫星搭载的三线阵CCD相机推扫的月表前视/正视影像,影像分辨率为512像素×8745像素。θ=0.6时由SIFT算法提取的匹配点数为839个;θ=0.8时由SIFT算法提取的匹配点数为903个。各算法匹配效果见表 2。
3.2.2前视/后视影像像对Ⅱ(2)是“嫦娥一号”卫星搭载的三线阵CCD相机推扫的月表前视/后视影像,影像分辨率为512像素×8745像素。θ=0.6时由SIFT算法提取的匹配点数为703个;θ=0.8时由SIFT算法提取的匹配点数为781个。各算法匹配效果见表 2。
| 序号 | 所用方法 |
|
| Ⅰ |
|
| Ⅱ(1) |
|
| Ⅱ(2) |
|
通过两个指标对试验结果进行分析:
(1) 计算效率:统计不同算法在误匹配率不同时运算效率的变化情况,比较结果见图 6。
(2) 可靠性:以沿主光轴拍摄的像对I和“嫦娥一号”卫星搭载的三线阵CCD相机推扫的月表前视/后视影像为例(θ=0.6),分析不同算法的匹配可靠性。分析结果见表 3。

|
| 图 6 运算效率比较 Fig. 6 Comparison of computation efficient |
当SIFT的阈值不同时,同名点的误匹配率随之变化。图 6比较了各算法在不同误匹配率时的运行效率。从图中可以看出,随误匹配率提高,RANSAC算法的运行时间显著的增加,运算效率明显降低,而本文提出的RANDOM-BAYSAC、RATIO-BAYSAC和OVERLAP-BAYSAC算法的运算效率则在误匹配率变化时仍表现平稳。
| 序号 | 内容 | RANSAC | RATIO- BAYSAC | OVERLAP- BAYSAC | 分析 /(%) |
| I |
|
| II(2) |
|
本文试验结果表明,针对不同影像,基于不同正确点先验概率估计方法的算法能将运算效率提高至少2倍以上,保留的正确匹配和匹配正确率也有不同程度的提高。
文章引入了一种通用的基于随机概率正确点先验概率估计方法,又提出了另外两种有针对性的正确点先验概率估计方法,3种方法给出的总是估计值,尽管能得到良好的试验结果,但这样的值不是精确的。在以后的研究中,可以设法获得更加精确的正确点先验概率,并能通用于不同影像中,就能得到更可靠的结果。
| [1] | QU Tianwei, AN Bo, CHEN Guilan. Application of Improved RANSAC Algorithm to Image Registration[J]. Journal of Computer Applications, 2010, 30(7):1849-1852. (曲天伟, 安波, 陈桂兰. 改进的RANSAC算法在图像配准中的应用[J]. 计算机应用, 2010, 30(7): 1849-1852.) |
| [2] | ZHU Q, WU B, XU Z. Seed Point Selection Method for Triangle Constrained Image Matching Propagation[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(2): 207-211. |
| [3] | YOU J, BHATTACHARYA P. A Wavelet-based Coarse-to-fine Image Matching Scheme in a Parallel Virtual Machine Environment[J]. IEEE Transactions on Image Processing, 2000, 9(9): 1547-1559. |
| [4] | LOWE D G. Distinctive Image Feature from Scale-invariant Keypoints[J]. International Journal of Computer Vision. 2004, 60(2): 91-110. |
| [5] | YANG Xuemei, GONG Junbin, WANG Peng, et al. Registration Algorithm for SAR and Optical Images Based on Improved SIFT[J]. Aerospaced Control, 2010, 28(6): 13-17. (杨雪梅, 龚俊斌, 王鹏, 等. 基于改进SIFT的SAR图像与可见光图像配准[J]. 航天控制, 2010, 28(6): 13-17.) |
| [6] | GONG Junbin, ZHANG Dazhi, YANG Xuemei, et al. Automatic Registration Algorithm for SAR and Optical Images with Rotation and Scale Invariability[J]. Journal of Astronautics, 2011, 32(6): 350-358. (龚俊斌, 张大志, 杨雪梅, 等. 抗旋转和缩放的SAR与可见光图像自动配准算法[J]. 宇航学报, 2011, 32(6): 350-358.) |
| [7] | YUE Chunyu, JIANG Wanshou. An Automatic Registration Algorithm for SAR and Optical Images Based on Geometry Constraint and Improved SIFT[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 570-576. (岳春宇, 江万寿. 几何约束和改进SIFT的SAR影像和光学影像自动配准方法[J]. 测绘学报, 2012, 41(4): 570-576.) |
| [8] | ZHANG Ka, SHENG Yehua, YE Chun. Digital Close-range Stereo Image Matching Based on Digital Parallax Model and Improved SIFT Feature[J]. Acta Geodaetica et Cartographica Sinica, 2012, 39(6): 624-630. (张卡, 盛业华, 叶春. 基于数字视差模型和改进SIFT特征的数字近景立体影像匹配[J]. 测绘学报, 2012, 39(6): 624-630.) |
| [9] | YAO Wenwei, ZHANG Zhibin, LI Guo, et al. Improvement of Image Matching Algorithm SIFT[J]. Geomatics and Information Science of Wuhan University, 2011, 26(6): 67-70. (姚文伟, 张智斌, 李国, 等. 图像匹配算法SIFT 的改进[J]. 武汉大学学报: 信息科学版, 2011, 26(6): 67-70.) |
| [10] | LI Fangfang, XIAO Benlin, JIA Yonghong, et al. Improved SIFT Algorithm and Its Application in Automatic Registration of Remotely-sensed Imagery[J]. Geomatics and Information Science of Wuhan University. 2009, 34(10): 1245-1250. (李芳芳, 肖本林, 贾永红, 等. SIFT算法优化及其用于遥感影像自动配准[J]. 武汉大学学报: 信息科学版, 2009, 34(10): 1245-1250.) |
| [11] | BOTTERILL T, MILLS S, GREEN R. New Conditional Sampling Strategies for Speeded-up RANSAC[C]//Proceedings of British Machine Vision Conference: BMVC 2009, London: British Machine Vision Association, 2009: 223-233. |
| [12] | LI Ersen, ZHANG Baoming, LIU Jingzheng, et al. The Application of SIFT Feature Matching Method in the Automatic Relative Orientation[J]. Science of Surveying and Mapping, 2008, 33(5): 16-18. (李二森, 张保明, 刘景正, 等. SIFT特征匹配技术在自动相对定向中的应用[J]. 测绘科学, 2008, 33(5): 16-18.) |
| [13] | MAINS J, CHUM O. Randomized RANSAC with Td,d Test[J]. Image and Vision Computing, 2004, 22(10): 837-84. |
| [14] | ZHANG Z Y. Determining the Epipolar Geometry and Its Uncertainty: A Review[J]. International Journal of Computer Vision, 1998, 27(2): 161-198. |
| [15] | FISCHLER M A, BOLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. |
| [16] | TORR P H S, MILRRAY D W. The Development and Comparision of Robust Methods for Estimating the Fundamental Matrix[J]. International Journal of Computer Vision. 1997, 24(3): 271-300. |
| [17] | FAN Xuedong. Base on the Fundamental Matrix Study of Matching Algorithm[D]. Changsha: Central South University, 2006. (范学栋. 基于基本矩阵的匹配算法研究[D]. 长沙: 中南大学, 2006.) |
| [18] | WANG Dongliang, XIAO Jianhua, WAN Youchuan, et al. Aerial Route Design Approach for Stereomapping Based on Stereomodel Overlap[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 188-193. (王东亮, 肖建华, 万幼川, 等. 基于立体模型重叠度的航空摄影航线设计[J].测绘学报, 2011, 40(2): 188-193.) |
| [19] | CUI Tengfei, CHEN Shengbo, WANG Jingran. Three-dimensional Modeling of the Lunar Surface Based on Stereo Camera Onboard Chang’e Orbitor[J]. Remote Sensing for Land & Resources, 2009, 4(32): 31-34. (崔腾飞, 陈圣波, 王景然. 基于“嫦娥卫星”三线阵CCD立体相机的月球表面三维建模[J]. 国土资源遥感, 2009, 4(32): 31-34.) |
| [20] | LI Qiaozhi, ZHANG Wuming, YAN Guangjian, et al. Simulation of Three-line CCD Satellite Images of the Moon[J]. Journal of Beijing Normal University, 2007, 43(3): 298-302. (李巧枝, 张吴明, 阎广建, 等. 月球卫星三线阵CCD影像模拟[J]. 北京师范大学学报: 自然科学版, 2007, 43(3): 298-302.) |