2. 南通大学 地理科学学院,江苏 南通 226007
2. School of Geographic Science, Nantong University, Nantong 226007, China
地图综合涉及空间数据的尺度变换问题,是地图学中最具挑战性和创造性的研究领域之一[1, 2]。由于建筑物在大比例尺地形图的数值载负量和面积载负量中均占有很大比重,因而建筑物多边形的化简是大比例尺地图综合的重要内容[3]。地图上多边形表现为由轮廓线围成的区域,其综合的基础是线综合[4]。早期的线综合主要是对局部有序点集直接处理实现化简,较为典型的方法有距离法、角度法、Lang法、Opheim法、光栅法等[5, 6, 7, 8, 9, 10, 11]。这些方法具有简单、高效、易于实现等优点,但往往存在整体形态难以保持、自相交、起始点敏感等难点问题。建筑物化简不同于一般的线化简,其轮廓是闭合曲线,局部形态又表现为直角形、任意折线、曲线或其组合形态,化简时需要综合考虑轮廓形态、面积等的保持[12]。虽然一些线化简算法被改进如基于面积保持的Douglas-Peucker改进算法[13]用于多边形化简,但均难以兼顾建筑物形态和面积保持。近些年来诸多学者从全局考虑相继提出多边形化简方法,如针对直角转折的建筑物,通过建立外接矩形或进行矩形差分组合判断凹凸部面积进行取舍实现化简[12, 14, 15];建立三角网进行全局控制,再对凹凸部进行填充、删除或夸大[16, 17, 18, 19],该类方法需要对所有特征点进行三角剖分再对三角形逐一判别、处理,复杂度较高,且对于复杂多边形仍需寻求新的策略以避免边界相交[16]。可见全局处理方法虽有优势,但也难以兼顾效率、特征保持和避免自相交等严格要求。
考虑到建筑物多边形化简实质上是对组成建筑物数据的空间点进行删除或者移位,而空间点的重要性直接受到邻近点及其相对关系的影响。因此,本文提出的邻近四点法(adjacent four-point method,AFPM)借鉴早期的线化简方法,并基于对建筑物轮廓形态和面积大小的保持考虑,将线化简中对局部三点或多点拓展为对邻近四点化简,有针对性地采取全局检查消除自相交现象,并探讨了起始点的选取方案,实现对建筑物多边形的快速有效化简。
2 AFPM的基本思路 2.1 几个基本概念 2.1.1 最小可视长度阈值建筑物多边形的化简应保持人眼对其图形在视觉感受上的一致性,如有长度小于规定阈值(一般以综合目标图上的0.3 mm为标准)的短边则需要化简[20]。因此,将人眼在图上能够分辨的最小长度所对应的实地距离称为最小可视长度阈值,以其作为建筑物多边形化简最基本的判别依据。
2.1.2外延角一般建筑物的边界主要由一些垂直线段构成,但也有些建筑物的形状并不规整,特别是在制图过程中,还需要经常对建筑物进行合并,使得地图上很多多边形呈现不规则形态。因此,多边形上邻近四点构成的3条边中首末两条边的延长线一般有一夹角α,本文称该夹角为邻近四点组合的外延角。
2.1.3 近似平行与近似共线考虑到方法的普适性和综合要求,本文将建筑物多边形中邻近四点组合的外延角小于10°,视其首末两条边为近似平行,大于170°时视为近似共线。
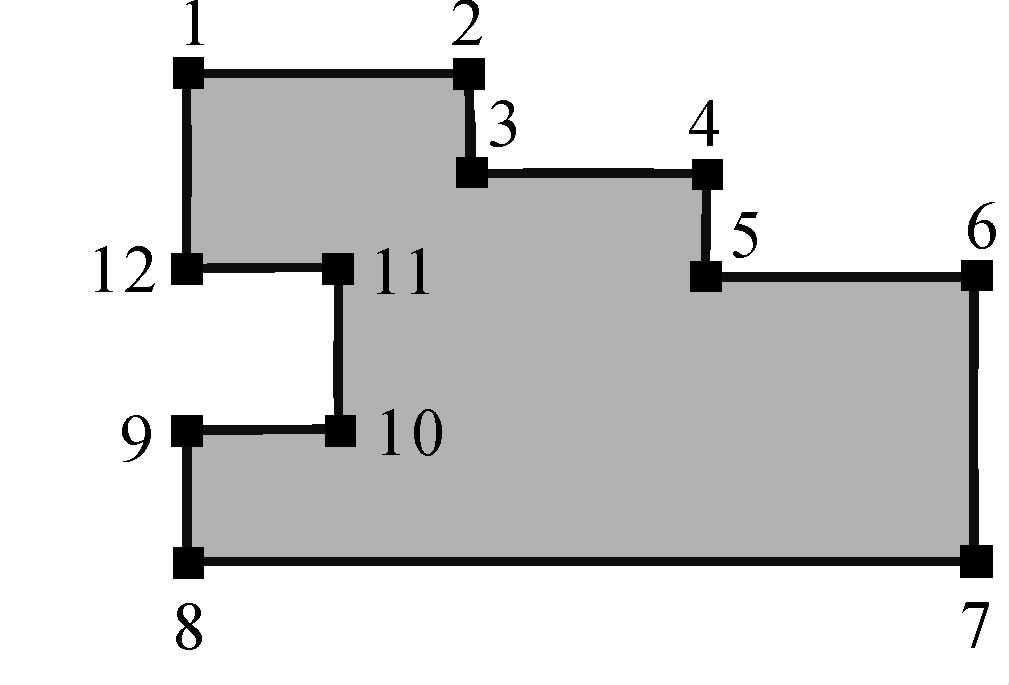
2.2基本思路早期的线化简方法如垂距法、偏角法等采用三点为基本单元,但用三点来化简建筑物有诸多不妥之处。首先,对矩形建筑物综合时需充分考虑其形状的直角化特点,采用三点法化简难以顾及直角形态和面积大小,其他线化简方法如Lang算法[9]、Opheim算法[10, 11]、DP算法[21]等也是如此;此外,多边形的化简关键在于依据比例尺的变化程度,评估建筑物多边形外部轮廓的凸凹状态及其相互联系,进而采取填凹或者扩大凹凸部等处理手段,而凸、凹部形态至少要四个邻近点才能描述,如图 1中的5、6、7、8和9、10、11、12四点。邻近四点即多边形上三条相邻边,还可以描述多边形上的梯形形态如3、4、5、6四点;而且其首末两条边的距离决定了该局部组合在地图上的可见程度。因此,以多边形上相邻四点作为基本处理单元,可通过判断其构成的三边中首末两条边的距离来确定采取删除或移位处理进行化简。对于局部线化简方法的执行顺序依赖、拓扑异化等缺点[6, 7, 8],可单独采取针对性措施如选取合适的特定起始点、全局检查消除自相交等加以改善,实现建筑物的快速有效化简。
|
| 图 1 建筑物多边形 Fig. 1 Building polygon |
根据建筑物多边形凹凸部的不同情形对基本处理单元作了分类定义,按顺序取建筑物多边形(特征点按顺时针或逆时针排列皆可)上的邻近四点1、2、3、4,设S12、S23、S34分别为对应两点间的距离,SV为目标比例尺下最小可视长度阈值。
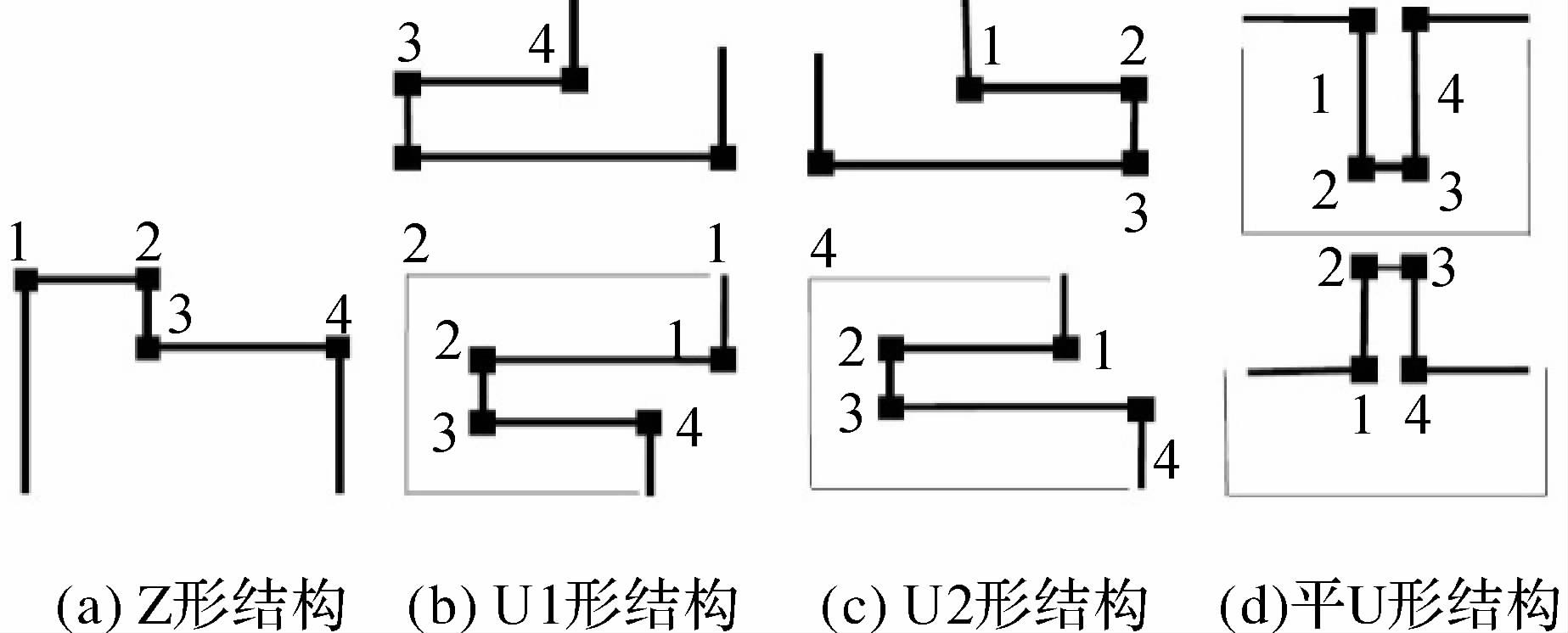
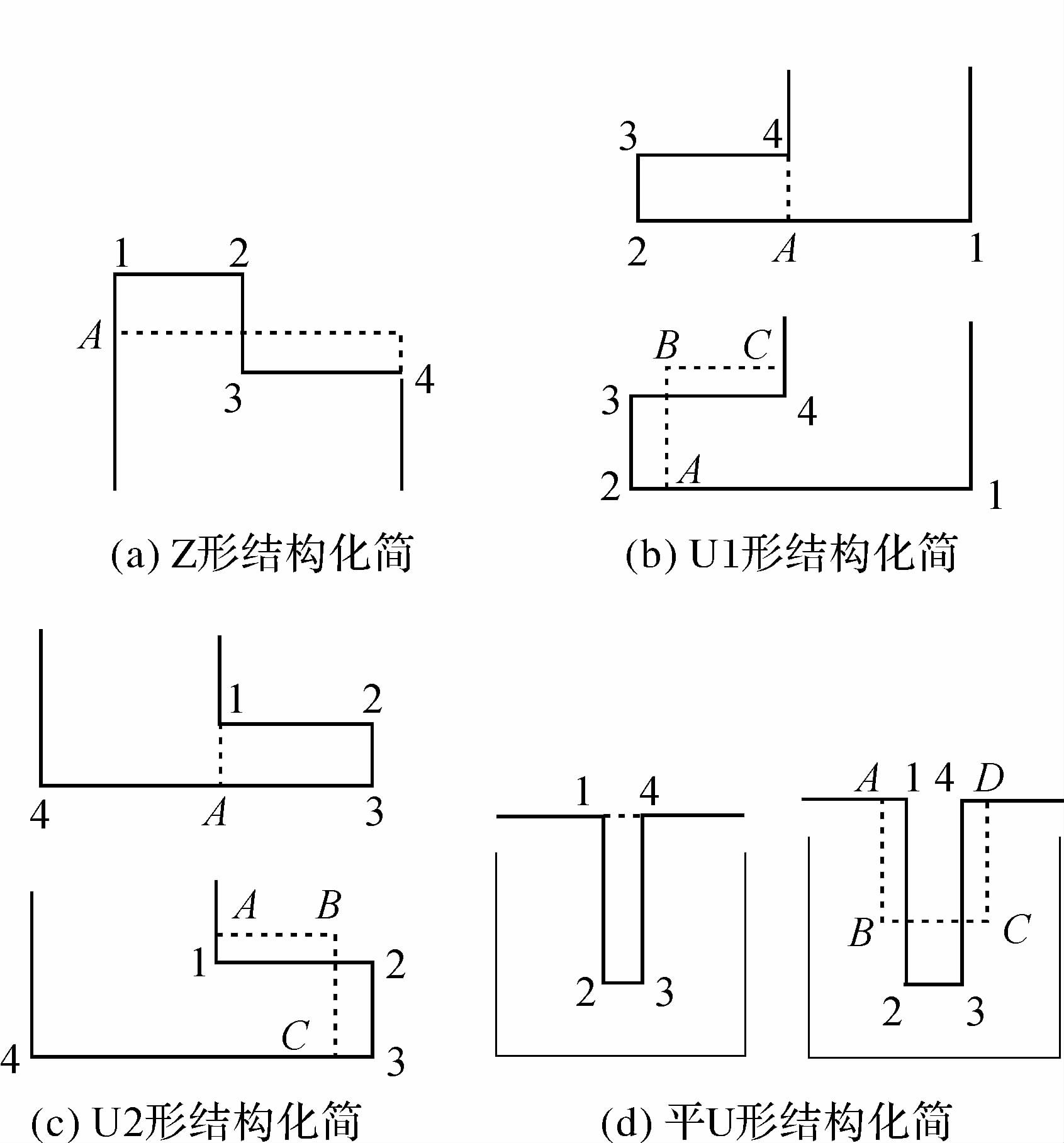
定义1:若1、4两点位于线段23两侧,将该四点组合结构称为“Z形”结构,如图 2 (a)所示;否则称之为“U形”结构,如图 2(b)—(d)所示,该结构涵盖了多边形中的凹、凸部形态。
在具体化简过程中按照四点组合构成的三边中首末两条边长度即S12、S34的不同,对U形结构又做了进一步区分。
定义2:若S12>S34,称该结构为U1形,如图 2 (b)所示。
定义3:若S12
定义4:若S12=S34,称该结构为平U形,如图 2 (d)所示。
|
| 图 2 邻近四点组合结构 Fig. 2 Structure of adjacent four-point groups |
需要指出的是由于数据采集误差、制图不规范等原因,使得地图上建筑物多边形中的平U形结构寥寥无几,出于方法合理性考虑,本文选取最小可视长度阈值的1/5作为缓冲距离,对以上定义做出如下修正定义。
定义5:U形结构中,若S12>S34且S12-S34>SV/5,称该结构为U1形;若S12
要辨别不同的邻近四点组合结构,首先要判断1、4两点相对于线段23的位置关系,设1、2、3、4点的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4),则1、4两点是否位于线段23的两侧可根据下列公式中same的值进行判断[22]
式中,dx=x3-x2;dy=y3-y2;dx1=x1-x2;dy1=y1-y2;dx2=x4-x3;dy2=y4-y3。same<0时,1、4两点在线段23的两侧,即为Z形结构;same>0时,1、4两点在线段23的同侧,即为U形结构。然后可根据定义5进一步辨别不同的U形结构,具体判别公式在此不作赘述。 4 基于AFPM的建筑物多边形化简 4.1 邻近四点组合结构的化简
街区的化简意味着在基本保持形态特征和面积大小的同时,通过减少轮廓线的冗余细节使得街区能更简洁有效地表达[20],AFPM的着手点是对不同邻近四点组合进行处理使其满足综合要求。在实际地图上四点组合并不全是直角形态,甚至经常出现尖角、点重合、多点共线等复杂情况。此时需要对多边形先进行削尖处理,目的是削除尖角并使四点组合中间两点的距离能够反映首末两条边的近似距离,为进一步化简作准备。
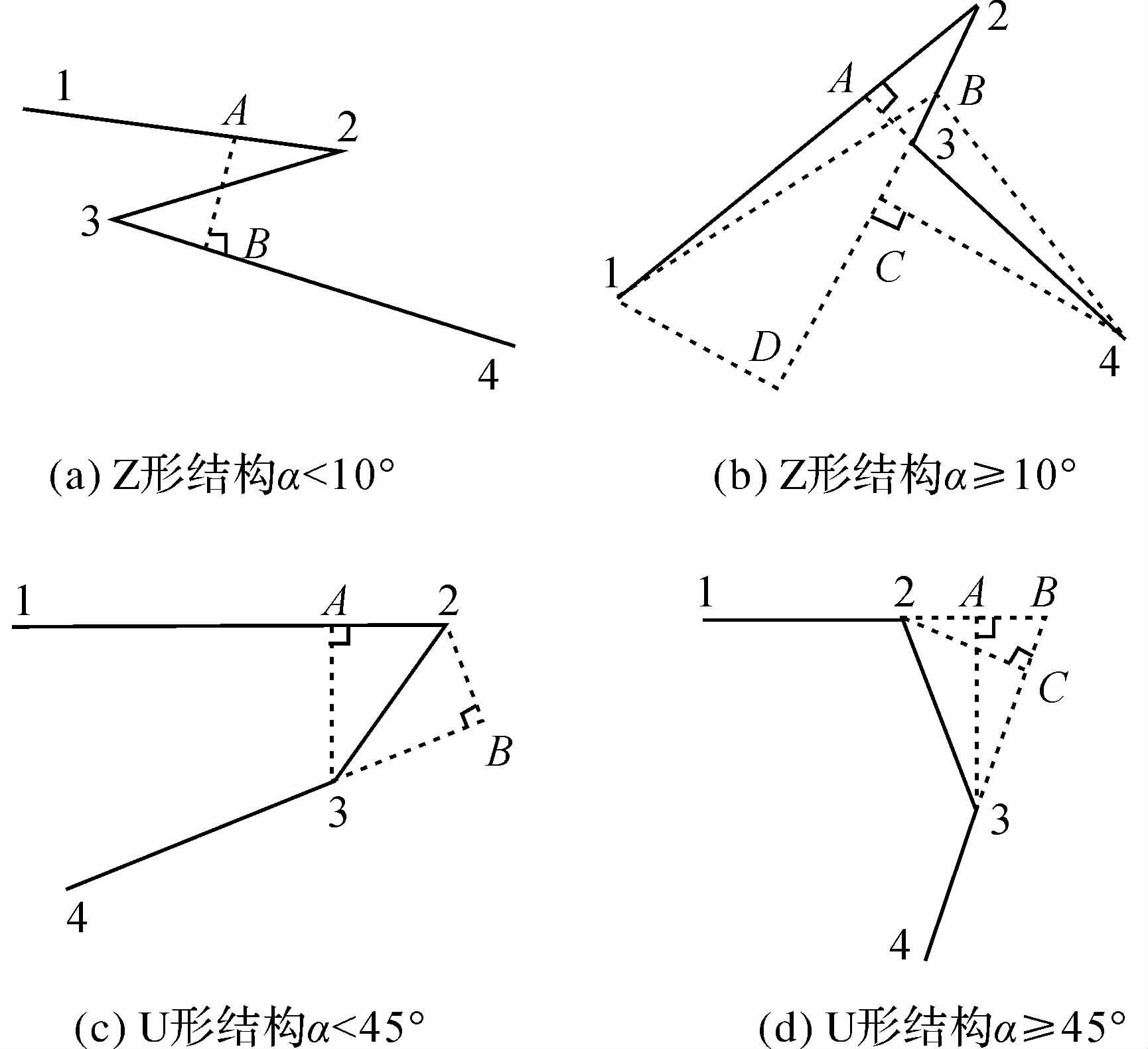
取建筑物上邻近四点组合1、2、3、4,其外延角为α,设S12、S23、S34、SAB、SBC、SCD分别为相应两点间的距离,2点到34边的距离为S1,3点到12边的距离为S2,SV为目标比例尺下最小可视长度阈值。其中,S1、S2直接或间接反映了四点组合构成的三边中首末两边的距离关系,是判断是否需要削尖的重要依据;而削尖后S23可近似反映该距离,若S23<SV则在目标比例尺下是无法辨识的,需要对特征点进行删除或移位,否则不需化简。下面介绍具体的削尖和化简操作。
4.1.1 削尖处理(1) 若为Z形结构,S1<SV或S2<SV且首末两条边近似平行,取中间边23的中点向其余两条边中的较长边作垂线(长度相同时取首边),垂线及其延长线分别交首末边于A、B点,则1、A、B、4为处理结果,如图 3 (a)所示。
(2) 若为Z形结构,S1<SV或S2<SV且首末两条边不近似平行,如图 3 (b)所示,则删除3点,将2点按23方向移位至B处,为尽量保持面积不变,根据1、4两点至23边的垂线长度S1D、S4C和2、3点的距离S23,设定位移量为S2B=S23S4C/(S1D+S4C)。
|
| 图 3 削尖处理 Fig. 3 Removing sharp corners |
(3) 若为U形结构,只有当S1、S2都小于SV时才进行削尖。本文设定45°为角度限值,当四点组合的α角小于45°取边12、34中较长边(长度相同时取首边)的对应垂线段作为新边,如图 2 (c),削尖后四点组合变为1、A、3、4点。
(4) 若为U形结构,S1
(1) Z形结构化简,删除2、3点并将1点按23方向移位至A点,4点按相反方向移至B点。遵循点所在边长度越大位移量越小的原则,分别设定1、4点的移位权重为q1=S34/S12+S34,q2=S12/S12+S34,则点的位移量为其移位权重与23的模即S23的乘积。移位结果如图 4 (a)所示(虚线为化简结果)。
(2) 若为U1形且S23 S34 < S2V ,则凹凸面积过小,直接删除2、3点并将4点按32移位至A点,如图 4 (b)上图所示。
(3) 若为U2形且S12 S23 < S2V ,删除2、3点并将点1按23移位至A,如图 4 (c)上图所示。
(4) 若为U1形且S23 S34 ≥S2V ,则其面积较大需要保留并作夸大处理,将2、3、4点分别移位至A、B、C点,遵循化简前后面积不变且图形清晰可辨的原则,因此要求移位后SAB=SV并且SABSBC=S23S34,如图 4 (b)下图所示。
|
| 图 4 邻近四点组合化简 Fig. 4 Simplification of adjacent four-point groups |
(5) 若为U2形且S12 S23 ≥S2V 则也进行夸大,移位1、2、3点至A、B、C点,要求移位后SAB=SV且SABSBC=S12S23。处理结果如图 3 (c)下图所示。
(6) 剩余情况按照平U形处理。若S12 S23 < S2V 或S23 S34 < S2V ,则直接删除该2、3点,如图 4 (d)上图所示;否则,对该结构进行夸大,分别移动1、2、3、4点至A、B、C、D,要求使SBC=SV且SABSBC=S12S23。移位后效果如图 4 (d)下图所示。
4.2 建筑物多边形化简 4.2.1 化简规则基于以上结构划分和判别处理来化简建筑多边形,基本目标是化简完成后建筑物多边形任何局部在目标比例尺下都是清晰可辨的,并较大限度地保持多边形的轮廓形状和面积。由于采用局部控制整体策略,因此更需要注意整个化简过程的完备性。使用该方法对整个多边形化简时应遵循以下规则。
规则1:化简过程必须遍历多边形数据所有不同的邻近四点组合,以保证化简完成后每条边以及局部结构在图上都是可见的。
规则2:化简邻近四点组合前必须先进行削尖处理。
规则3:削尖处理后,只有四点组合中间两点的距离小于目标比例尺下最小可视长度阈值时,才对该结构进行化简,否则不作处理,向后重新取点。
规则4:鉴于以上规则,对不同四点组合结构进行化简后,由于点位可能发生变化,因此应该重新确定下一步从哪个点位开始继续取邻近4点:① Z形结构,取点位置不变;② U形结构,若有删除操作,取点位置减一位,若采用夸大操作,取点位置增加两位。
4.2.2化简过程给定一建筑物多边形(特征点按顺时针或逆时针排列皆可),以其化简起始点重新排序,设其排序后按点号0,1,2,…,N-1共N个点组成。假定多边形首末点即第0点和第N-1点位置相同,每次从P点向后取4点进行判别处理,初始取点位置P为0,“%”为取余运算符。基于以上各规则,可以得到整个建筑物多边形的化简流程:
步骤1:若P=N-1或N<4,到步骤5;否则取P%N、(P+1)%N、(P+2)%N、(P+3)%N四个点。
步骤2:判别4点组合的结构并判断是否需要削尖处理,如不需削尖,P加1到步骤1。
步骤3:进行削尖处理,如削尖后点数有变化进入步骤1,否则进入下一步。
步骤4:判断邻近四点组合是否需要化简,如不需要P加1到步骤1。
步骤5:对不同4点组合结构进行化简,同时及时更新多边形点数N并按照规则4更新取点位置P,到步骤1。
步骤6:将首点位置赋给末点,结束化简。
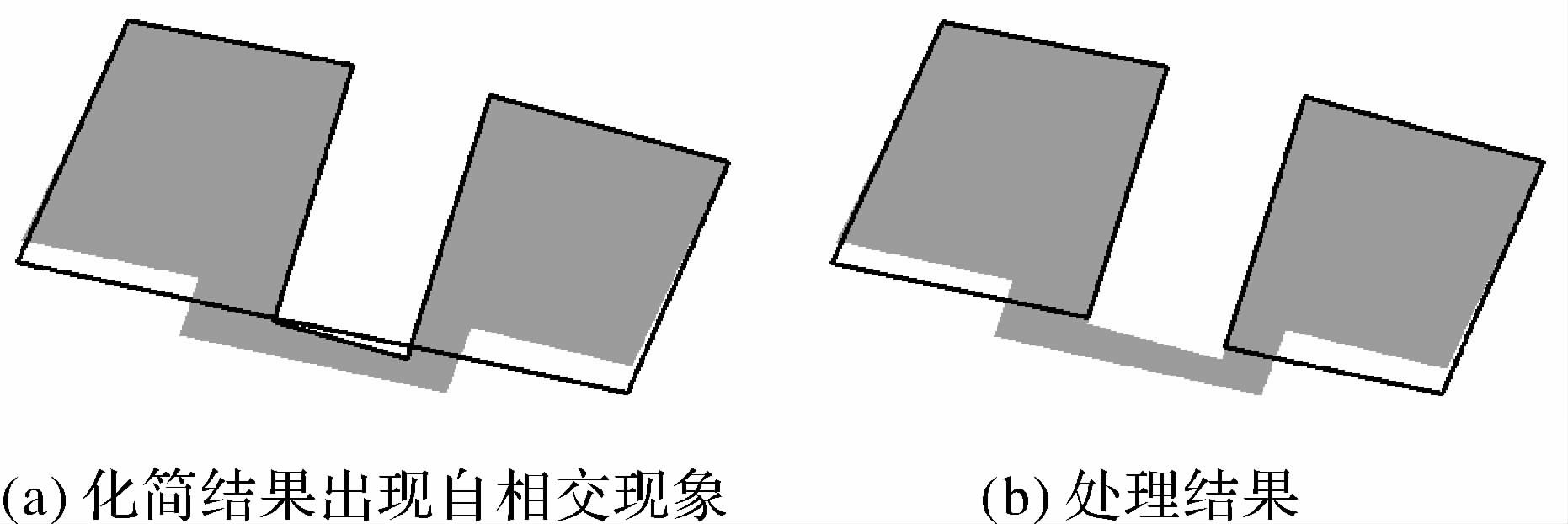
4.3 建筑物多边形化简中的特殊情形地图上建筑物形态繁杂多样,无论采用局部化简还是整体处理都很难完全消除自相交现象。上述过程对点位相隔较远但位置又相距较近的边难以觉察,造成化简结果中可能存在过窄区域甚至自相交现象。如图 5 (a)所示,这是在建筑物化简中较为特殊的情况,但化简时必须考虑到并尽可能避免产生该种冲突[20]。因此上述化简完成后,还需要进行全面检查,对存在空间冲突的建筑物进行处理以保证其清晰可辨以及整体显示效果。文献[12]将直角形建筑物多边形中边相距过近甚至重合的现象称为共线性,提出了通过判断线段距离和投影区域面积识别该结构并确定夸大或者删除,该方法同样适用于非直角型建筑物化简的冲突处理。
|
| 图 5 建筑物多边形化简中的特殊情形 Fig. 5 Peculiar status of building polygon simplification |
本文在Visual Studio 2010环境下结合ArcGIS Engine 10对提出的方法进行了试验和分析。试验选取1∶10000比例尺下庐山地区部分面积在500m2以上的建筑物群为试验数据,以图上距离3mm为最小可视长度阈值进行了多组化简试验。
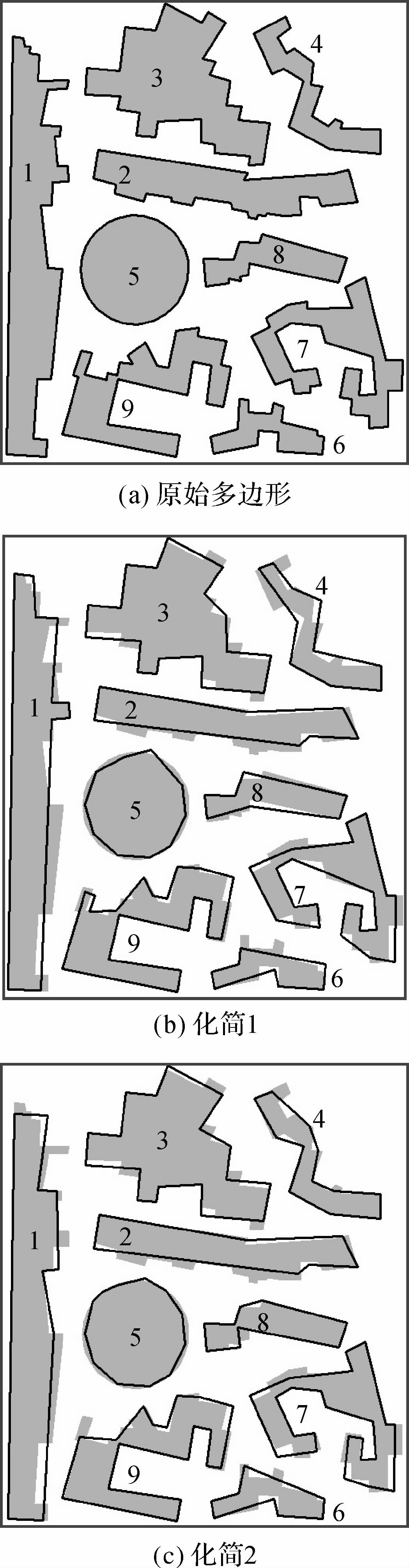
5.1 起始点选取由于本文采用局部处理策略,从不同起点开始化简得到的结果可能不同。分别选取建筑物上最大外接圆上的点、最长边起点作为化简起始点进行了1、2两组试验,发现选取的729个多边形中有36个化简结果不一致,观察它们的轮廓多呈现连续的短小起伏形态,如图 6为筛选其中较为典型的一组多边形,试验统计数据如表 1。可以看出以最长边开始化简结果优于最大外接圆上的点,因本文提出的方法主要依据四点组合中边的长度和距离进行处理,最大外接圆上的点更易受其所在的不同邻近四点结构中相邻点的影响,也很有可能被删除,因此不具优势。所以应选取建筑物多边形上最长边起点作为化简起始点。
|
| 图 6 起始点敏感问题 Fig. 6 Problem of starting point |
| 多边形 | 原始边长 | 原始面积 | 化简 | 边长 | 变化率/(%) | 面积 | 变化率/(%) |
| 1 | 545.60 | 4335.68 | 1 | 488.17 | 10.5 | 4082.12 | 5.8 |
| 2 | 473.91 | 13.1 | 4173.02 | 3.8 | |||
| 2 | 337.17 | 2364.16 | 1 | 303.71 | 9.9 | 2110.91 | 10.7 |
| 2 | 303.59 | 10.0 | 2112.06 | 10.6 | |||
| 3 | 381.67 | 3605.31 | 1 | 350.67 | 8.1 | 3581.31 | 0.7 |
| 2 | 356.46 | 6.6 | 3572.73 | 0.9 | |||
| 4 | 268.63 | 1184.72 | 1 | 223.63 | 16.8 | 1181.87 | 0.2 |
| 2 | 229.76 | 14.5 | 1148.87 | 3 | |||
| 5 | 176.51 | 2469.28 | 1 | 169.19 | 4.1 | 2169.97 | 12.1 |
| 2 | 170.11 | 3.6 | 2231.51 | 9.6 | |||
| 6 | 190.64 | 788.56 | 1 | 156.04 | 18.1 | 721.31 | 8.5 |
| 2 | 159.07 | 16.6 | 790.81 | 0.3 | |||
| 7 | 452.07 | 2193.61 | 1 | 416.59 | 7.8 | 2136.69 | 2.6 |
| 2 | 414.00 | 8.4 | 2137.21 | 2.6 | |||
| 8 | 195.38 | 1047.86 | 1 | 180.25 | 7.7 | 1010.15 | 3.6 |
| 2 | 192.94 | 1.2 | 1039.03 | 0.8 | |||
| 9 | 450.92 | 2334.68 | 1 | 415.01 | 8.0 | 2359.02 | 1.0 |
| 2 | 397.49 | 11.8 | 2334.49 | 0.0 | |||
| 注:表中各变化率是指化简前后的差值与原始值的比率。 | |||||||
建筑物多边形化简中特征点的提取、基本形状以及面积的保持是评定各种算法精度和效率的重要标准[23]。为检验方法的可行性,对建筑物多组化简试验数据作了统计,如表 2所示。
| 化简 方式 | 阈值 /m | 比例尺 | 多边形 个数 | 点 数 | 周长总和 /m | 面积总和 /m2 | 点数变化 率/(%) | 周长变化 率/(%) | 面积变化 率/(%) |
| 原始数据 | 1∶10000 | 729 | 9333 | 180057.5 | 1765209.6 | ||||
|
直接 化简 |
7.5 | 1∶25000 | 729 | 7053 | 172026.1 | 1768095.1 | 24.4 | 4.5 | 0.2 |
| 15.0 | 1∶50000 | 729 | 5692 | 154229.2 | 1720224.3 | 39.0 | 14.3 | 2.5 | |
| 22.5 | 1∶75000 | 729 | 5155 | 136655.8 | 1601546.5 | 44.8 | 24.1 | 9.3 | |
| 渐进式 化简 |
7.5 | 1∶25000 | 729 | 7053 | 172026.1 | 1768095.1 | 24.4 | 4.5 | 0.2 |
| 15.0 | 1∶50000 | 729 | 5272 | 152667.2 | 1740529.2 | 43.5 | 15.2 | 1.3 | |
| 22.5 | 1∶75000 | 729 | 4252 | 131214.4 | 1652604.1 | 54.4 | 27.1 | 6.4 | |
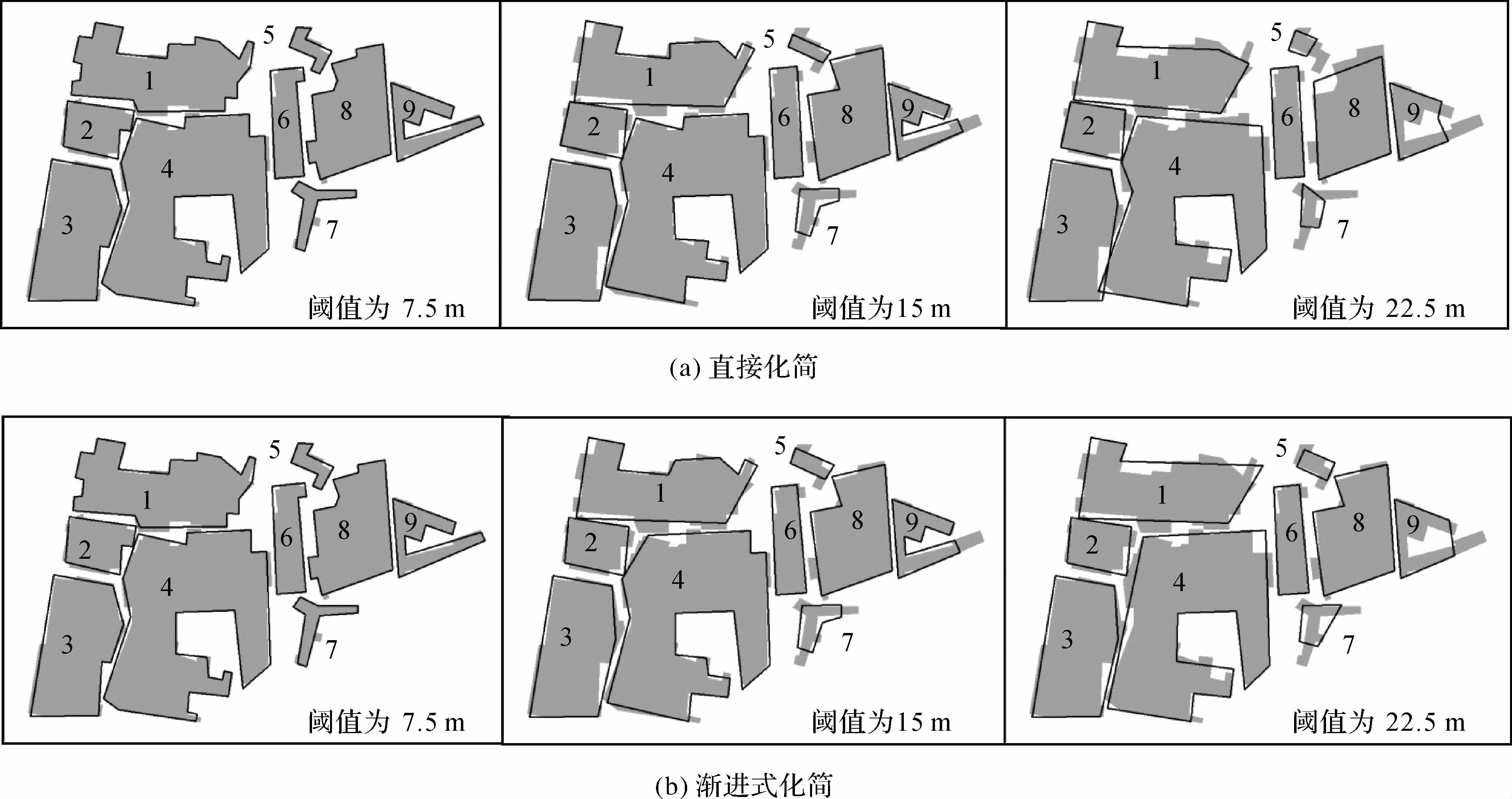
可以看出化简有效地减少了特征点数量,且比例尺跨度较小时能够较好地保持多边形轮廓和面积大小。设置较大阈值直接进行化简时,建筑物面积变化较大,分析其原因主要是化简时阈值过大导致删除点增多。但渐进式化简在多边形特征点筛选、面积保持方面明显优于直接化简。图 7为其中较为典型的一组多边形的化简试验,灰色区域为原始建筑物,深色轮廓为化简结果。
与统计数据类似,从图中可以看出本方法化简效果较好,但另外也发现以下问题:
(1) 设置较大阈值直接化简时不仅面积变化较大,个别多边形的轮廓形态或位置也出现较偏差,如阈值为22.5m时多边形5、7等。这也主要因为设置大阈值对四点结构化简时移位幅度较大、删除点较多,导致多边形的中心位置、形态及面积变化较大。但同样可采用渐进式化简缓解上述问题。
(2) 相邻多边形化简后出现相交现象。这是由于相邻多边形局部靠得太近,移位、删除点等操作引起相交。解决的办法是化简前先进行合并。
|
| 图 7 采用不同阈值的化简 Fig. 7 Simplification on different thresholds |
基于AFPM化简建筑物多边形是用简单思路来解决复杂的综合问题的一次尝试,主要出发点是满足综合后的可视化要求,综合考虑了最短边长度、最小角、最小距离和最小面积等可视化参数约束[24],取得了较好的综合效果。总结该方法的特点如下:能较好地保持建筑物多边形的轮廓特征和面积,考虑了化简尺度,化简结果基本符合制图规范;以四点组合为基本处理单元,基本操作流程只是简单的取点、判断和处理,容易实现,效率较高;采用局部控制整体兼顾全局检查等策略,对局部算法的不足有所改善。需要指出的是,本文仅考虑单个建筑物的化简且在比例尺跨度较大时需采取渐进式化简。在今后的研究中将进一步探讨方法在顾及建筑物群组空间关系、配合多边形合并、移位处理以及跨大尺度条件下的改进。
| [1] | LI Weisheng. Conceptual Frameworks and an Example for Neighboring Relationships in Computer Supported Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(3): 231-238.(李伟生. 地图制图自动综合中相邻关系的概念框架及例子[J]. 测绘学报, 1995, 24(3): 231-238.) |
| [2] | DENG Hongyan, WU Fang, ZHAI Renjian, et al. Study of Generalization Knowledge Base for Quality Control Based on Database[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 121-127, 134.(邓红艳, 武芳, 翟仁健, 等. 基于数据库的保质设计制图综合知识库研究[J]. 测绘学报, 2008, 37(1): 121-127, 134.) |
| [3] | LIU Pengcheng, AI Tinghua, DENG Jifang. Simplification and Rectangularity of Building-polygon Based on Least Squares Adjustment[J]. Journal of China University of Mining & Technology, 2008, 37(5): 699-704.(刘鹏程, 艾廷华, 邓吉芳. 基于最小二乘的建筑物多边形的化简与直角化[J]. 中国矿业大学学报, 2008, 37(5): 699-704.) |
| [4] | TIAN Peng, ZHENG Kougen, PAN Yunhe. Polygon Simplification Based on Strip-tree in Scaleless GIS [J]. Journal of Software, 2001, 12(10): 1495- 1502. ( 田鹏, 郑扣根, 潘云鹤. 基于Strip-Tree的无级比例尺GIS多边形化简技术[J]. 软件学报, 2001, 12(10): 1495- 1502. ) |
| [5] | MCMASTER R B. Automated Line Generalization[J]. Cartographica: The International Journal for Geographic Information and Geovisualization, 1987, 24(2): 74-111. |
| [6] | ZHANG Chuanming, PAN Mao, WU Huanping, et al. Study on Simplification of Contour Lines Preserving Topological Coherence [J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2007, 43(2): 216-222.(张传明, 潘懋, 吴焕萍, 等. 保持拓扑一致性的等高线化简算法研究[J]. 北京大学学报:自然科学版, 2007, 43(2): 216-222.) |
| [7] | QIAN Haizhong, WU Fang, CHEN Bo, et al. Simplifying Line with Oblique Dividing Curve Method[J]. Acta Geodaetica et Cartographica Sinica, 2008, 36(4): 443-449.(钱海忠, 武芳, 陈波, 等. 采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报, 2008, 36(4): 443-449.) |
| [8] | CHEN Yi, PENG Rencan, ZHENG Yidong, et al. Line Generalization Based on Douglas Both-sides Multi-way Tree[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 310-315.(陈轶, 彭认灿, 郑义东, 等. 基于 Douglas 双侧多叉树的曲线综合算法研究[J]. 测绘学报, 2010, 39(3): 310-315.) |
| [9] | LANG T. Rules for Robot Draughtsmen[J]. Geographical Magazine, 1969, 42(1): 50-51. |
| [10] | OPHEIM H. Smoothing a Digitized Curve by Data Reduction Methods[M]. Amsterdam:North-Holland Publishing Company, 1981: 127-135. |
| [11] | OPHEIM H. Fast Data Reduction of a Digitized Curve[J]. Geo-processing, 1982, 2: 33-40. |
| [12] | GUO Qingsheng. The Method of Graphic Simplification of Area Feature Boundary as Right Angle[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(3): 255-258.(郭庆胜. 以直角方式转折的面状要素图形简化方法[J]. 武汉测绘科技大学学报, 1999, 24(3): 255-258.) |
| [13] | HUANG Wanli, DAI Wenyuan, YU Shan. Using Modified Douglas-Peucker Algorithm Based on Area Preservation to Simplify Polygons[J]. Science Technology and Engineering. 2009, 9(24): 7325-7328.(黄万里, 戴文远, 余珊. 基于面积保持的Douglas-Peucker改进算法的多边形化简[J]. 科学技术与工程, 2009, 9(24): 7325-7328.) |
| [14] | GUO Renzhong, AI Tinghua. Simplification and Aggregation of Building Polygon in Automatic Map Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(1): 25-30.(郭仁忠, 艾廷华. 制图综合中建筑物多边形的合并与化简[J]. 武汉测绘科技大学学报, 2000, 25(1): 25-30.) |
| [15] | BAYER T. Automated Building Simplification Using a Recursive Approach[J]. Cartography in Central and Eastern Europe, 2010: 121-146. |
| [16] | AI Tinghua, GUO Renzhong, CHEN Xiaodong. Simplification and Aggregation of Polygon Object Supported by Delaunay Triangulation Structure[J]. Journal of Image and Graphics, 2001, 6(7): 703-709.(艾廷华, 郭仁忠, 陈晓东. Delaunay 三角网支持下的多边形化简与合并[J]. 中国图象图形学报, 2001, 6(7): 703-709.) |
| [17] | ZHANG Jing, ZHOU Ye, LIU Yu. An Improved Algorithm for SDS Model Based Polygon Simplification and Aggregation[J]. Journal of Image and Graphics, 2006, 11(7): 1010-1016.(张晶, 周烨, 刘瑜. SDS 模型化简合并多边形的一个改进算法研究[J]. 中国图象图形学报, 2006, 11(7): 1010-1016.) |
| [18] | QIAN Haizhong, WU Fang, ZHU Kunpeng, et al. A Generalization Method of Street Block Based on Dimension-reducing Technique [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 102-107.(钱海忠, 武芳, 朱鲲鹏, 等. 一种基于降维技术的街区综合方法[J]. 测绘学报, 2007, 36(1): 102-107.) |
| [19] | CHEN Wenhan, LONG Yi, SHEN Jie, et al. An Improvement Selection Method of GIS Information Generalization Based on Rough Set Structure Recognition and Progressive Simplification of the Concaves of Building Polygon Based on Constrained D-TIN[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5): 584-587.(陈文瀚, 龙毅, 沈婕, 等. 利用约束 D-TIN 进行建筑物多边形凹部结构识别与渐进式化简[J]. 武汉大学学报: 信息科学版, 2011, 36(5): 584-587.) |
| [20] | WANG Huilian, WU Fang, ZHANG Linlin, et al. The Application of Mathematical Morphology and Pattern Recognition to Building Polygon Simplification[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 269-276.(王辉连, 武芳, 张琳琳, 等. 数学形态学和模式识别在建筑物多边形化简中的应用[J]. 测绘学报, 2005, 34(3): 269-276.) |
| [21] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. Cartographica: The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112-122. |
| [22] | ZHOU Peide. Computational Geometry: Analysis and Design of Algorithms[M]. Beijing:Tsinghua University Press, 2000: 138-139.(周培德. 计算几何——算法分析与设计[M]. 北京: 清华大学出版社, 2000: 138-139.) |
| [23] | TONG Xiaohua, XIONG Guofeng. Aggregation, Simplification and Adjustment of Building Polygon Objects in Multi-scale Map Generalization[J]. Journal of Tongji University:Natural Science, 2007, 35(6): 824-829.(童小华, 熊国锋. 建筑物多边形的多尺度合并化简与平差处理[J]. 同济大学学报: 自然科学版, 2007, 35(6): 824-829.) |
| [24] | WANG L, ZHANG J, YAO G. The Analysis and Experiments of Least-squares Method for Settlements Generalization[C]//Proceedings of Information Science and Technology 2012 International Conference.Wuhan: ICIST, 2012:210-214. |