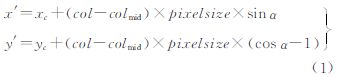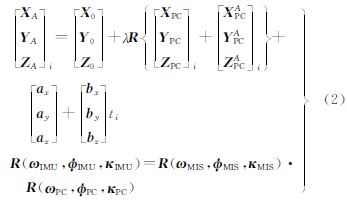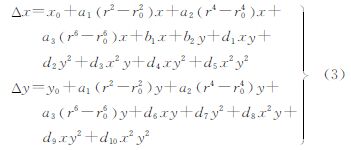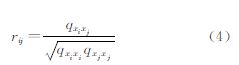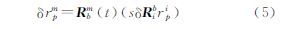2. 国家基础地理信息中心,北京 100830
2. National Geomatic Center of China,Beijing 100830,China
1 引 言
线阵相机是随着GNSS/IMU技术的成熟推出的机载多线阵传感器系统,因此相机的标定涵盖相机内方位元素误差、光学系统畸变差,以及GNSS/IMU单元与相机之间的相对关系等内容。特别是IMU坐标轴与相机坐标轴之间的夹角实际是不可能平行的,它们之间的相对位置用仪器无法精密量测,只能通过试验场检校来测定。
目前普遍采用的相机检校方法是自检校技术,自检校模型的研究和应用已有多年的历史[1, 2, 3]。国内对线阵相机标定也作了一定研究,文献[4, 5, 6]介绍了采用地面试验场自检校法解算线阵相机的系统误差参数,但都必须要利用地面检校,几何定标的结果取决于地面检校场中控制点网的数量、分布、精度等要素。基于地面检校场对三线阵相机ADS40 影像的区域网平差数学模型也进行了相关研究,分析了不同几何条件、控制点数量对影像几何定位精度的影响[7, 8, 9]。但是对于基于航带设计方案脱离地面控制点完成相机检校工作的相关报道很少,在国内也是首次对该方法开展研究和试验工作。
本文从理论上分析机载线阵传感器影像定向过程中的误差来源,参考基于地面试验场的检校平差方式,围绕利用航线结构去除各项误差参数之间相关性的关键问题以及航线优选展开了分析与研究。通过设计检校和验证数据进行试验,证明了双航高十字往返航线进行相机检校的可行性和正确性。
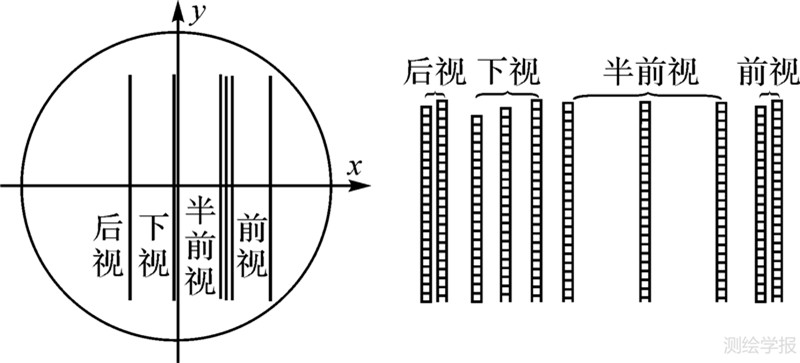
2 误差模型 2.1 相机误差模型线阵传感器和传统的框幅式相机在几何特性上有较大的不同。以ADS40三线阵扫描成像航摄仪为例,它在同一像平面内垂直于飞行方向平行排列10条CCD线阵,如图 1所示。每条CCD线阵包含12 000个像元,像元尺寸6.5 μm,所有像元在焦平面上的中心坐标(xc,yc)都记录在相机文件里面。
|
| 图 1 ADS40 CCD线阵排列 Fig. 1 Arrangement of ADS40’s CCD Lines |
每条扫描行由同一焦平面上的不同CCD线阵成像获取,每个像元的内定向参数不同,式(1)为像点的焦平面坐标系x′Oy′与影像坐标系rOc之间的转换关系
式中,α为CCD线阵与焦平面坐标系y轴的倾角,col是CCD影像列号,colmid是位于中心位置的CCD影像列号,pixelsize为像元尺寸。相机检校文件是每一个CCD像元在焦平面上的坐标值。
2.2 POS误差模型线阵传感器将飞行方向上采集的一系列以时间序列的定向点作为投影中心,基于POS系统记录定向点曝光时刻的位置、姿态数据,通过差分GPS、卡尔曼滤波、坐标系转换、拉格朗日多项式内插等处理获得每条扫描行的外方位元素。
理想状态下,POS系统获得的外方位元素即可作为实际观测值。但是通常情况下,POS系统受GPS天线偏心分量、GPS时间漂移、IMU视准轴偏心角等误差影响,直接观测获得的外方位元素存在明显的系统误差[10]。对应于时刻ti,式(2)为直接观测的外方位元素与实际外方位元素之间的转换关系
式中, XA、YA、ZA为在地面坐标系下的坐标; X0、Y0、Z0为地面坐标系与POS坐标系之间的转换参数; λ为摄影比例尺因子;R为地面坐标系与相机坐标系之间的旋转矩阵; XPC、YPC、ZPC为成像时刻相机在地面坐标系下的坐标; XAPC、YAPC、ZAPC为天线中心与相机曝光中心的距离; ax、ay、az、bx、by、bz为GPS漂移参数; ωMIS、φMIS、κMIS为IMU视准轴误差。式(2)中相机姿态矩阵R(ωPC,φPC,κPC)是在IMU坐标系下测量的,R(ωMIS,φMIS,κMIS)是IMU轴系与相机坐标轴系之间的视准轴误差旋转矩阵。由于ADS40和IMU集成经过精密安置,IMU偏移误差很小,地面分辨率在150 mm以内,相对位置而言,IMU轴系与相机坐标轴系无法严格平行,一般精度在分级,相当于3个像素的误差。因此,进行IMU视准轴误差补偿是ADS40检校的必需内容。
2.3 检校平差模型对线阵CCD传感器几何畸变特性的研究表明,几何变形特征较为复杂,涉及CCD线阵在焦平面内的平移、旋转、缩放、弯曲变形。但在实际工作中,还是可以利用传统的引入附加参数的自检校算法。如式(3)表示的Brown自检校平差模型[11]适用于线阵相机CCD线阵几何变形误差的建模
式中共有17个附加参数,x0和y0表示像主点坐标,附加参数组(a1,a2,a3)表示径向畸变参数,(b1,b2)表示仿射变形参数,(d1,d2,…,d10)表示胶片变形以及非径向畸变差参数;r为像点在像片上的径距;r0为一给定常量。除沿用了一部分框幅式相机的参数,如主点偏移、主距变化、仿射变形参数,在模型中取消了不适用的有关参数,如CCD压平引起的变形不会超过2μm,CCD线阵线性形变不超过1μm,以避免参数过度化引起的模型失真。 3 参数相关性分析及航线结构优选 3.1 参数相关性分析众所周知,内定向参数与外方位元素、附加参数与附加参数、附加参数与坐标未知数之间具有相关性。式(4)为任意两个未知数之相关系数,其值为
表 1是附加参数之间相关系数阵的一个计算实例。可以看出,(a1,a2,a3)径向畸变参数、(d9,d10)参数之间存在强相关,这种相关与多项式模型的高次项有关。考虑到平差中不可能允许有两个彼此强相关的附加参数,应当对具有强相关的附加参数进行剔除。
| a1 | a2 | a3 | d1 | d2 | d3 | d4 | d5 | d6 | d7 | d8 | d9 | d10 | |
| a1 | 1.0 | ||||||||||||
| a2 | -1.0 | 1.0 | |||||||||||
| a3 | 0.9 | -1.0 | 1.0 | ||||||||||
| d1 | -0.1 | 0.0 | 0.0 | 1.0 | |||||||||
| d2 | -0.3 | 0.3 | -0.3 | 0.0 | 1.0 | ||||||||
| d3 | 0.0 | 0.0 | 0.0 | -0.4 | -0.1 | 1.0 | |||||||
| d4 | -0.1 | 0.0 | 0.0 | 0.3 | 0.3 | -0.1 | 1.0 | ||||||
| d5 | 0.3 | -0.3 | 0.2 | 0.0 | -0.5 | 0.1 | -0.6 | 1.0 | |||||
| d6 | 0.3 | -0.2 | 0.1 | -0.2 | -0.3 | 0.0 | -0.6 | 0.6 | 1.0 | ||||
| d7 | 0.0 | 0.0 | 0.0 | -0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | |||
| d8 | 0.1 | -0.3 | 0.3 | 0.3 | -0.1 | 0.0 | 0.4 | 0.1 | -0.5 | 0.0 | 1.0 | ||
| d9 | 0.0 | 0.0 | 0.0 | -0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.6 | 0.0 | 1.0 | |
| d10 | 0.0 | 0.0 | 0.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.7 | 0.0 | -0.9 | 1.0 |
表 2由协因素阵求出附加参数与坐标未知数的相关系数阵。从表中看出,相关性最大的附加参数为主距与高程,相关系数为1。其次是像主点与线元素,相关系数为0.7。另外,(d4,d5,d6)与角元素φ也表现出一定的相关性,相关系数为0.5左右。
| f | x0 | y0 | a1 | b1 | b2 | d1 | d2 | d3 | d4 | d5 | d6 | d7 | d8 | |
| XO | 0.0 | -0.7 | 0.1 | 0.0 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| YO | 0.0 | 0.1 | -0.7 | 0.0 | -0.1 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| ZO | -1.0 | -0.3 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| O | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 | 0.0 | 0.4 | 0.0 | 0.0 | 0.1 | 0.0 | -0.1 | -0.1 | 0.2 |
| P | -0.3 | -0.3 | 0.0 | -0.2 | -0.1 | 0.0 | 0.1 | 0.2 | 0.0 | 0.5 | -0.4 | -0.6 | 0.0 | 0.2 |
| K | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 |
在几何检校光束法平差过程中要同时解求这些相关参数,但它们之间可能会互为补偿和取代,并不能确保自检校平差有可靠的结果。为了消除或减少几何定标中各种参数的相关性及对定标结果的影响,在几何检校中对地面检校场会提出一些要求,如地面要有一定的高差等。
3.2 航线结构优选目前,对于在不同几何条件下改善附加参数相关的可测定性问题,可以采用增大旁向重叠、改变飞行方向或采用十字交叉飞行来提高参数的可测定性[12]。其基本原理是,从三线阵影像上提取大量连接点,经区域网平差整体解算得到成像数据的附加参数近似值。
IMU系统的陀螺比例因子变化会导致飞行方向相反的两条航线姿态角元素的跳变[13, 14],为了提高检校的可靠性,引入往返飞行的相邻两条航线作为一个整体求解视准轴误差。为了保证航线方向和垂直于航线方向的精度一致性和区域的稳定性,拟采用往返飞行交叉航线。
当在一个航高上时,焦距与Z坐标完全相关,需要增加控制点约束才能求解。焦距变化量Δf与坐标变化量ΔZ的关系为:Δf=ΔZf/Z。当在两个航高上时,地面高程变化ΔZ不变,但对Δf的影响不同,因此焦距与高程的相关性可以进行分离[15, 16, 17, 18, 19]。根据垂直高度上的差异计算得到Δf来确定视准轴误差。视准轴误差3个偏心角与主距误差在光束法平差中一并进行解求。
按文献[20]提出的式(5)建立视准轴误差与航高之间的几何关系表达式为
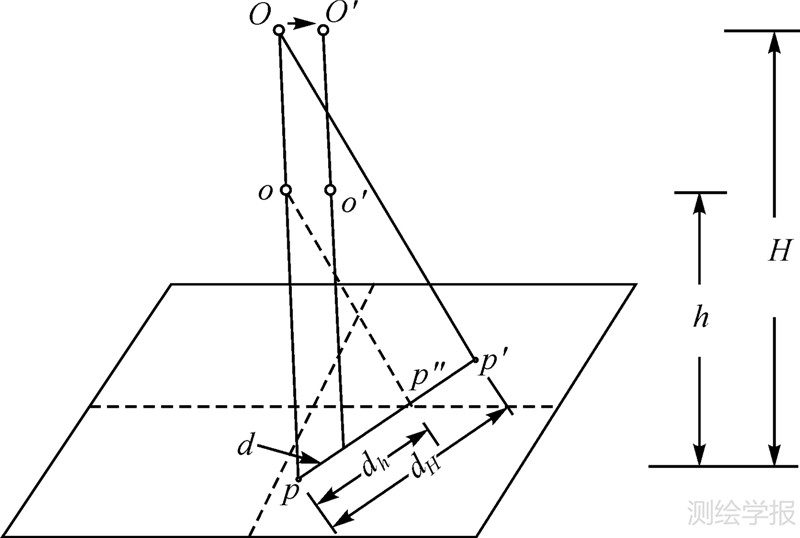
式中,δΔrpm为地面点的坐标偏移;Rbm(t)为IMU姿态角构成的旋转矩阵;s为摄影比例尺分母;Rib为IMU偏心角构成的旋转矩阵;rpi为像点坐标。从式(3)可以看出视准轴误差与航高成正比,若航高H引起像点位移dH,则航高h引起像点位移dh,而主点偏移引起的像点位移在航高H(h)上都是d,如图 2所示。
|
| 图 2 主点偏移与视准轴误差相关性 Fig. 2 The correlations between the principal point and misalignment parameters |
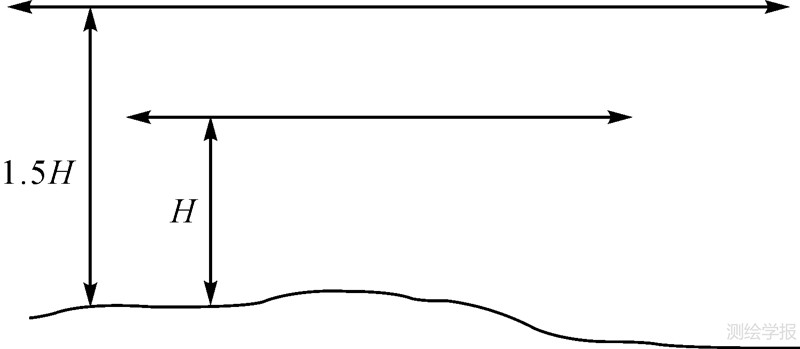
考虑到航线的地面覆盖范围、同名点的匹配精度等因素,大于1.5倍航高会导致航线重叠度降低;小于1.5倍航高,比例系数接近相关性增强,建议两个航高的比例关系为1.5倍,此时航线重叠度达到67%。
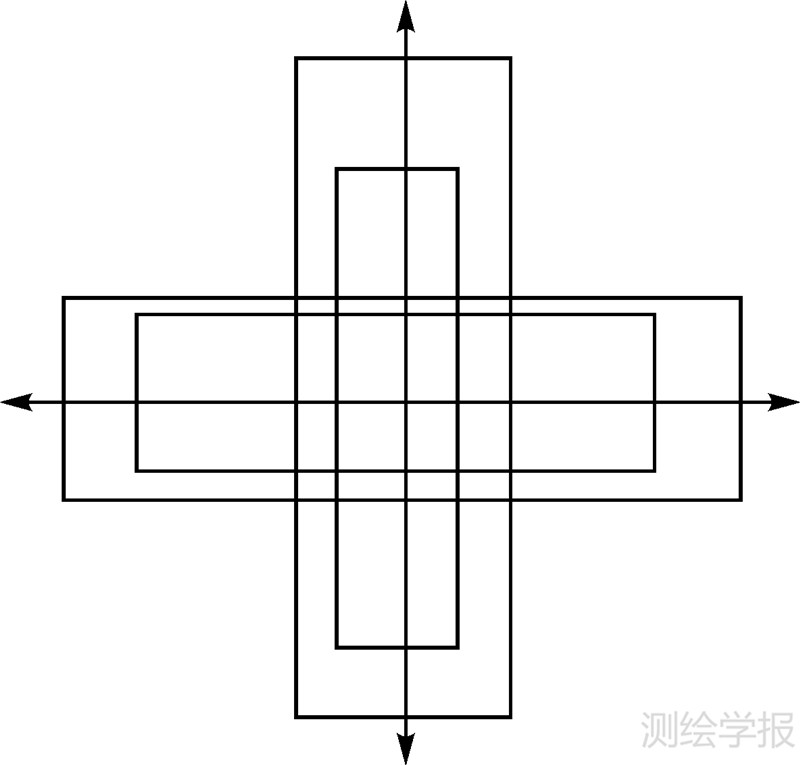
从上面的分析,线阵传感器几何定标可采用的航线结构如图 3和图 4。
|
| 图 3 双航高十字往返航线结构 Fig. 3 Structures of the two flight levels bi-directional cross flight line |
|
| 图 4 双航高的高度比例关系 Fig. 4 The block scale of the two flight levels |
用于试验的数据是2009—2011年在河南嵩山检校场获取的ADS40相机编号30053、30055的航空影像。其中30055数据两个航高为1250 m和1900 m,30053数据两个航高为600 m和1000 m。在试验中,也对本文基于航线结构的无地面控制点自检校方法和带控制点的自检校方法进行了比较。
4.2 检校结果和分析以30055相机为例,绕X、Y、Z轴为旋转轴的视准轴轴线夹角误差如表 3所示。
| rad | |||
| 视准轴误差 | φ | ω | κ |
| 检校前 | -0.000 409 441 | -0.014 890 213 | 0.005 349 507 |
| 检校后 | -0.000 412 242 | -0.014 854 570 | 0.005 362 958 |
| 改正值 | -0.000 002 801 | 0.000 035 643 | 0.000 013 451 |
由表 3可知,绕X轴旋转角φ改正值为-0.58″,绕Y轴旋转角ω改正值为7.35″,绕Z轴旋转角κ改正值为2.77″。如果以2000 m航高为例,ω改正值换算到地面上的投影误差为2 m,相当于1个像素的误差。比较三个角度的改正值可以看出,30055相机检校前Y方向上的精度要比于X方向的精度差。
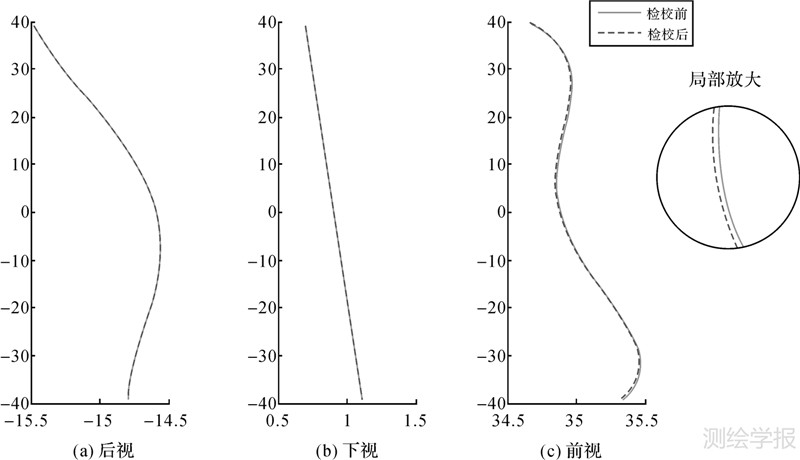
检校前后相机焦平面前视、下视、后视三条线阵的CCD像元排列如图 5所示,像元中心坐标值见表 4。
|
| 图 5 三线阵CCD像元排列 Fig. 5 Layout of three linear array CCD chip |
| mm | ||||||
| 波 段 | 0 | 6 000 | 12 000 | |||
| X | Y | X | Y | X | Y | |
| PAN B14A | -14.663 725 | -39.117 385 | -14.310 859 | -0.059 110 | -15.031 262 | 39.017 127 |
| GRNN00A | 1.327 075 | -39.279 315 | 1.166 624 | -0.128 601 | 1.012 498 | 39.022 558 |
| PAN F28A | 35.252 604 | 39.711 708 | 35.309 613 | 0.335 302 | 35.538 944 | -39.044 516 |
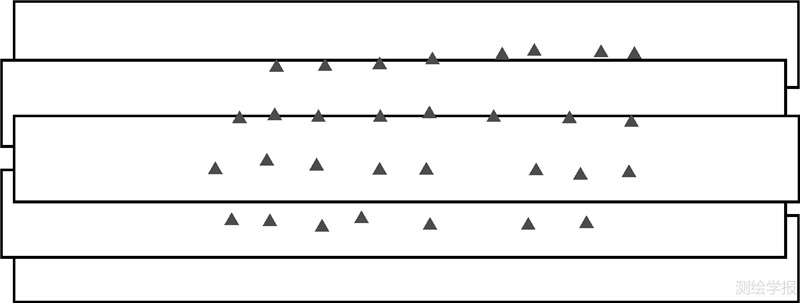
为了检验本文提出算法的结果,利用实际数据进行了检验验证,验证数据采用平行航线飞行5个航带,测区航线结构及控制点分布见图 6。相机30055选取1900 m航高数据,相机30053选取1000 m航高数据,量测地面控制点31个,区域网平差的几何精度如图 7所示。
|
| 图 6 航线结构及控制点分布 Fig. 6 The image block configuration and the GCP distribution |
|
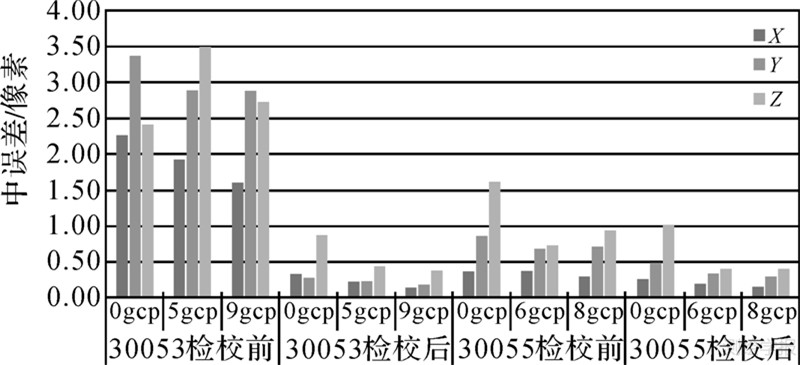
| 图 7 ADS40相机检校前后精度对比 Fig. 7 The comparison with accuracy results of three ADS40 sensors before/after calibration |
从试验结果可以看出,相机30053检校后平面精度由2.9个像素提高到0.2个像素,高程精度由2.7个像素提高到0.4个像素。相机30055检校后Y方向平面精度由0.7个像素提高到0.3个像素,高程精度由1像素提高到0.4像素。检校后无控制点平差的平面精度均达到了0.5像素,高程精度达到1像素,提高效果明显。
4.4 和利用地面控制点的检校方法的比较为了测定参数数值的可靠性,对本文方法和利用地面控制点的检校方法不同几何条件下的附加参数组进行对比检验,如表 5所示。C1航线结构所有附加参数的相关性都很低,使用双航高可以将像主点和视准轴误差之间的相关性减小到0.5,不影响检校结果的稳定性。从结果可知,两组参数数值之间无显著差异,C1航线结构的特点在于没有引入地面控制点,附加参数与坐标未知数之间的相关性都很小,相关性系数在0.3以内。
| 参数 单位 | f /mm | x0 /mm | y0 /mm | a1 /10-7 | b1 /10-4 | b2 /10-4 | d1 /10-8 | d2 /10-7 | d3 /10-7 | d4 /10-8 | d6 /10-5 | d7 /10-6 | d8 /10-8 |
| C1 | -62.713 | -0.02 | 0.02 | 1.30 | -5.57 | -2.16 | -2.7 | -9.3 | -1.16 | -7.73 | -1.17 | -3.8 | 7.5 |
| C2 | -62.709 | -0.05 | 0.01 | -0.6 | -6.45 | -1.22 | -3.4 | -11.8 | -1.22 | -6.36 | -1.16 | -3.4 | 8.2 |
| 注:C1,无地面控制点的双航高十字交叉往返飞行航线;C2,带地面控制点的水平+构架航线 | |||||||||||||
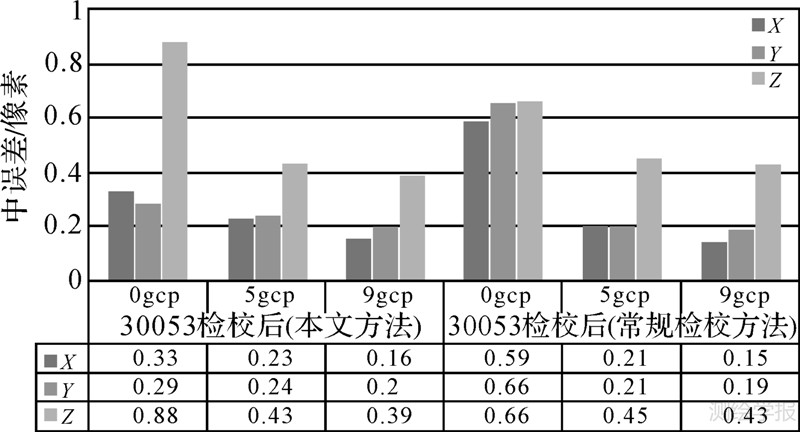
图 8给出了采用本文的方法和采用带控制点自检校的常规方法分别完成几何检校所达到定位精度的对比情况。
|
| 图 8 两种几何检校方法精度对比 Fig. 8 The accuracy comparison of two geometric calibration methods |
这个对比表明,选择5个控制点平差两种方法精度一致,平面精度达到0.2像素,高程精度为0.4像素。无控制点平差本文方法平面精度较高,为0.3像素,高程精度略低,为0.9像素。常规检校方法的局限性在于需要构建基于地面控制点的自检校平差模型,本文的方法不依靠地面检校场的航线结构方案,可以应用于无地面控制点情况下的相机检校。
5 结束语本文分别从理论和试验两个方面,阐述了用航线结构取代地面试验场进行线阵航空传感器检校的可行性。利用具体的ADS40影像数据进行试验,验证了双航高十字往返航线满足机载传感器几何检校精度的要求。试验结果表明,使用少量控制点平差即可得到稳定的结果:平面精度0.3像素,高程精度0.5像素。无控制点平差的平面精度0.5像素,高程精度1像素。
| [1] | KOCAMAN S, CASELLA V, FRANZINI M, et al. The Triangulation Accuracy of ADS40 Imagery over the Pavia Testsite[C/ CD] //Proceedings of the 2007 Conference of the Remote Sensing and Photogrammetry Society. Newcastle upon Tyne: ISPRS, 2007: 1-6. |
| [2] | HONKAVAARA E, ILVES R, JAAKKOLA J. Practical Results of GPS/IMU/Camera-system Calibration[C/CD]// Proceedings of International Workshop: Theory, Technology and Realities of Inertial/GPS Sensor Orientation. Castelldefels: [s.n.], 2003: 22-23. |
| [3] | SANDAU R, BRAUNECKER B, DRIESCHER H, et al. Design Principles of the LH Systems ADS40 Airborne Digital Sensor[C]// International Archives of Photogrammetry and Remote Sensing: 33(B1). Amsterdam: [s.n.], 2000: 258-265. |
| [4] | TU Xinru, XU Miaozhong, LIU Li. The Geometric Calibration of Airborne Three-line-scanner ADS40[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 78-83. (涂辛茹, 许妙忠, 刘丽. 机载三线阵传感器ADS40的几何检校[J]. 测绘学报, 2011, 40(1): 78-83.) |
| [5] | XU Miaozhong, TU Xinru. Geometric Calibration of ADS40 System Based on Test Field[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 771-775. (许妙忠, 涂辛茹. 基于定标场的ADS40系统几何检校[J]. 武汉大学学报: 信息科学版, 2011, 36(7): 771-775.) |
| [6] | WANG Tao, ZHANG Yongsheng, AHANG Yan, et al. Airborne Linear CCD Sensor Geometric Calibration Based on Self-calibration [J]. Acta Geodaetica et Cartographica Sinica, 2012,41(3): 393-400. (王涛, 张永生, 张艳, 等. 基于自检校的机载线阵CCD传感器几何标定[J]. 测绘学报, 2012,41(3): 393-400.) |
| [7] | ZHAO Shuangming, LI Deren. Experimentation of Adjustment Math Model for ADS40 Sensor[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 342-346. (赵双明, 李德仁. ADS40机载数字传感器平差数学模型及其试验[J]. 测绘学报, 2006, 35(4): 342-346.) |
| [8] | LIU Jun, WANG Donghong, LIU Jingxian, et al. IMU/DGPS Supported Block Adjustment of ADS40 Three Line Imagery Data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 55-60.(刘军, 王冬红, 刘敬贤, 等. IMU/DGPS系统辅助ADS40三线阵影像的区域网平差[J]. 测绘学报, 2009, 38(1): 55-60.) |
| [9] | LIU Jun, WANG Donghong, ZHANG Yongsheng, et al. Bundle Adjustment of Airborne Three Line Array Imagery Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2009, 37(4): 451-457.(刘军, 王冬红, 张永生, 等. 基于单位四元数的机载三线阵影像光束法平差[J]. 测绘学报, 2008, 37(4): 451-457.) |
| [10] | HINSKEN L, MILLER S, TEMPELMANN U, et al. Triangulation of the LH Systems’ ADS40 Using ORIMA GPS/IMU[C/CD]// International Archive of Photogrammetry, Remote Sensing and Spatial Information Sciences: 34(3A). Graz: [s.n.], 2002: 1-7. |
| [11] | BROWN D C. The Bundle Adjustment: Progress and Prospects[C]// International Archive of Photogrammetry: 2(III). Helsinki: [s.n.], 1976: 1-31. |
| [12] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Press of Wuhan University, 2002: 183-186.(李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉:武汉大学出版社, 2002: 183-186.) |
| [13] | CRAMER M, STALLMAN D. System Calibration for Direct Georeferencing[C]// International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences: 34(3A). Graz: [s.n.], 2002: 79-84. |
| [14] | YUAN Xiuxiao, YANG Fen, ZHAO Qing, et al. Boresight Misalignment Calibration of Integrated DGPS/IMU System[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1039-1043.(袁修孝, 杨芬, 赵青, 等. 机载POS系统视准轴误差检校[J]. 武汉大学学报: 信息科学版, 2006, 31(12): 1039-1043.) |
| [15] | TEMPELMANN U, HINSKEN L, RECKE U. ADS40 Calibration and Verification Process[C/CD]// Proceedings of International Workshop: Theory, Technology and Realities of Inertial/GPS Sensor Orientation. Castelldefels: [s.n.], 2003: 1-6. |
| [16] | HONKAVAARA E. Calibration Field Structures for GPS/IMU/Camera-system Calibration[J]. The Photogrammetric Journal of Finland, 2003, 18(2): 3-15. |
| [17] | SCHUSTER R, BRAUNECKER B. Calibration of the LH Systems ADS40 Airborne Digital Sensor[C/CD]// Proceedings of International Archives of Photogrammetry and Remote Sensing: 33(B1). Amsterdam: [s.n.], 2000: 288-292. |
| [18] | FUCHS T, ADIGüZEL M. Enhancement and Simplification of Leica ADS Calibration Process[C/CD]// Proceedings of European Calibration and Orientation Workshop EuroCOW. Casteldefells: [s.n.], 2010: 1-4. |
| [19] | JACOBSEN K. Aspects of Handling Image Orientation by Direct Sensor Orientation[C/CD]// Proceedings of the ASPRS Annual Meeting. St Louis: [s.n.], 2001: 1-8. |
| [20] | IP A W L. Analysis of Integrated Sensor Orientation for Aerial Mapping[EB/OL]. Calgary: Calgary University, 2005. [2012-01-12]. http://www.ucalgary.ca/engo_webdocs/NES/ 05.20204_ AlanIp.pdf. |