1 引 言
在空间数据尺度变换中随着表达空间的缩小会产生图形间的冲突,移位是一种解决这种冲突的有效操作[1, 2]。完备合理的移位在解决空间冲突时应满足以下两个条件:① 避免移位导致新的空间冲突,移位之后不在上下文中产生次生冲突;② 移位后能够保持空间群目标的相对位置和分布模式形态。
目前制图综合中移位主要基于两种思想,一是一次性调整相关冲突目标的空间位置,通过分析上下文环境下空间目标的冲突情形,计算出各相关目标需要移动的距离,一次性移位处理。在地图综合研究领域提出了多种方法,包括利用空间目标的中心点生成的三角网构建MST树,并由此计算每个空间目标的偏移量从而对空间目标进行移位[3, 4];根据空间目标分布密度划分区域进行多层次移位[5];将空间目标群作为一个完整的场,通过空间目标的Voronoi图来构建移位场,从而对建筑物进行移位[6]。这一类移位算法快速简单,能够较好地保持空间目标的分布形态,但是对于密集区域会因为移位而产生新冲突,只能通过后处理解决。第二种思想是引用优化技术通过多次迭代逐渐移动来解决空间目标的冲突。基于这种思想的移位算法包括利用模拟退火算法[7, 8]、遗传算法[9]、最小二乘算法[10, 11]、有限元方法[12]以及在有限元基础上利用弹簧模型进行移位的算法[13, 14]。利用迭代的思想对空间群目标进行移位能够较好地解决要素冲突,但是在多次移动中空间目标的分布模式往往被破坏,在迭代过程中“好的位置”的目标函数判断难以形式化、定量化建立,另外这类算法所需的计算量也比较大,而且每次运行的结果不同。
与其他地图综合算子相比,移位的显著特点在于上下文、目标群条件的考虑,该特征与空间场模型思想相吻合。基于场(域)的模型思想可以假定空间中的目标分布是某种力的平衡作用结果,就像重力场中的重力或电磁场中的磁力,在地图综合的删除、夸大、合并等操作中,力的平衡体系发生变化,通过位置调整来求得新的平衡,这便是移位。
运用物理学中的场论思想对移位过程建模,关键是场的表达与作用力的模拟,笔者前期研究[6]建立了移位场概念,以建筑物移位为例提出了移位中的等关系曲线,将冲突视为移位的斥力力源。但前期研究的移位模型只考虑了街道拓宽产生的单一力源,移位后可能会产生新的冲突,同时也可能破坏目标群的整体模式。为改进该方法本文提出一种多力源场模型,通过多源斥力的向量和计算得到最终移位的方向与偏移距离,来解决移位过程中多重冲突的问题。本文先分析文献[6]前期研究移位方法的不足,然后提出改进的多种力源的移位场模型,最后通过试验讨论改进方法在避免次生冲突、保持空间模式方面的特点。
2 单一力源移位场产生的问题在单一力源移位场模型中,利用Voronoi图构建空间目标群的无缝隙无重叠覆盖移位场。以移位场中空间目标剖分边界为力的作用对象。将外部收缩产生的向内挤压的力逐级递减向中心传递形成一系列的等势线。利用等势线确定空间目标受力大小及方向,从而对空间目标进行移位[6]。
单一力源移位场比较好地考虑了移位过程中的“传递性”与“衰减性”效应,但是由于只考虑了街道拓宽产生的“外力”作用,移位后可能产生次生冲突并破坏建筑物分布结构的完整模式。以图 1为例,单一力源移位场模型产生的问题包括:
(1) 破坏分布模式,如图 1(b)中所示A、B处的建筑群,移位后产生挤压或错位,破坏了原有的A区域的线性排列、B区域的折线排列模式。
(2) 加重局部冲突。图 1(b)中C、D、E区域原本就比较拥挤、已经存在一定冲突,在受到不同大小的作用力的情况下导致更加拥挤以致建筑物发生冲突。这种情况可以通过对Voronoi图分析快速地探测到冲突区域。
(3) 出现次生冲突。如图 1(b)中F、G区域,该区域建筑物移位前分布密度不大且没有冲突,在移位操作中由于受到不同方向的作用力,产生次生冲突,可以通过后处理解决。
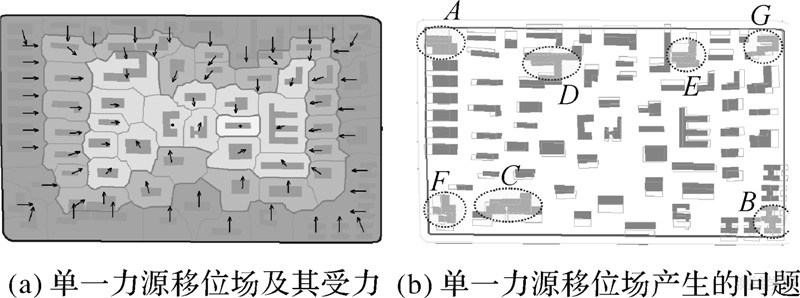
|
| 图 1 单一力源移位场产生的结果及问题 Fig. 1 The result and problems of single-source field model |
改进的移位场模型考虑空间冲突的产生来自多种力源,包括街道拓宽产生的外力、建筑物内部冲突产生的内力,以及次生冲突产生的内部斥力,多力源的探测是移位场模型建立的关键。空间目标密集区域容易在移位过程中产生冲突,空间分布密集特征需要定量化的计算方法。有很多参量可以用来体现空间目标分布的密集程度,包括空间目标与其影响范围的面积比、空间目标之间的距离等。距离直接影响移位后的空间目标是否冲突,本文采用距离作为冲突探测中的量化指标。多边形目标的距离有多种定义,本文采用空间目标的通视距离[16]来探测冲突。在空间目标群构建的Voronoi图[15]中,连接两个空间目标之间的区域为通视区域,通过计算通视区域的平均宽度可以得到通视距离。通视距离计算公式如下,其中,D为空间目标的通视距离,n为空间目标之间三角形的数目,hi为第i个三角形的高
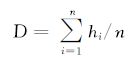
采用通视距离作为探测冲突的量化指标具有以下优点:① 提高计算效率,利用模型中构建的Voronoi图能够很快地计算出空间目标的通视距离;② 探测过程更准确,较之于欧氏距离,通视距离得到的是平均距离,能够更好地体现空间目标的现有冲突。
若任意相邻的两个空间目标Oi、Oj之间的距离Dij小于某一阈值Dmin,则位移后这两个空间目标可能发生冲突。令i、j在单一力源移位场模型中的移位距离分别为D(i)、D(j),则Dmin的值正比于|D(i)-D(j)|,同时空间目标之间需要保持一定的视觉辨析距离Dc(通常为图面0.4 mm),则有
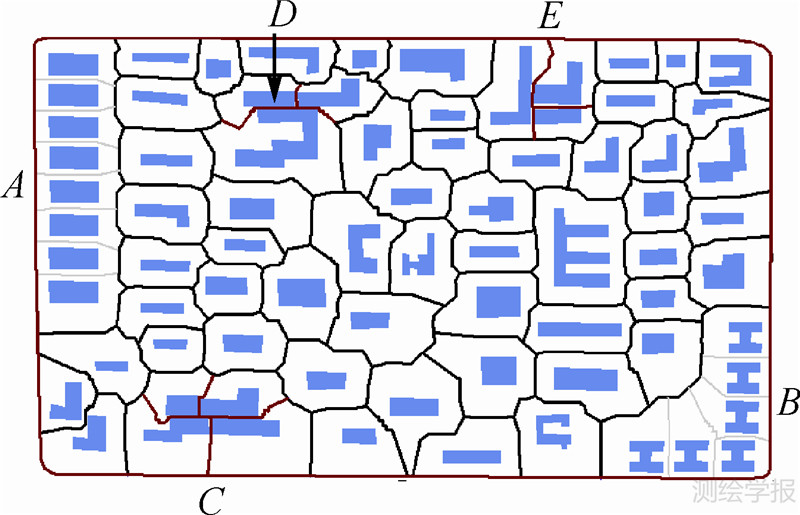
|
| 图 2 潜在冲突区域(C、D、E)与模式分布区域(A、B) Fig. 2 Area of conflicts(C、D、E)and area of spatial patterns(A、B) |
冲突边为移位场中的内力源,表现为斥力推动相邻目标移动,通过场的扩展逐渐向外扩散影响周围空间目标,其作用范围是一个衰减的过程。与冲突边相邻的空间目标设为0级目标,即该力源最直接作用的目标对象,然后依次向外递减从而得到内力场的等势线。顾及内力的影响范围不如街道拓宽外力作用强的特点,对内力效应作如下处理:① 不传递到所有空间目标而仅限定于内力源附近一定范围内,从多次试验的结果来看,内力的影响范围应该限制在距离冲突边3条等势线范围内得到的移位效果比较好,即邻近度大于或等于3的建筑物就不受该内力影响;② 内力源两侧空间目标受到的斥力fc的大小取决于冲突边两侧空间目标的距离Dij,距离越小则内力强度越大,但不超过外力大小。内力的大小同外力一样按照邻近度逐层递减,可以利用公式f(d)=fc-kd按线性衰减得到,方向由等势线的法线方向确定[6]。图 3(b)、(c)、(d)分别对应3个不同力源的内力场,矢量法表示的箭头的长短和方向描述了内力场中建筑物所受内力的情况。
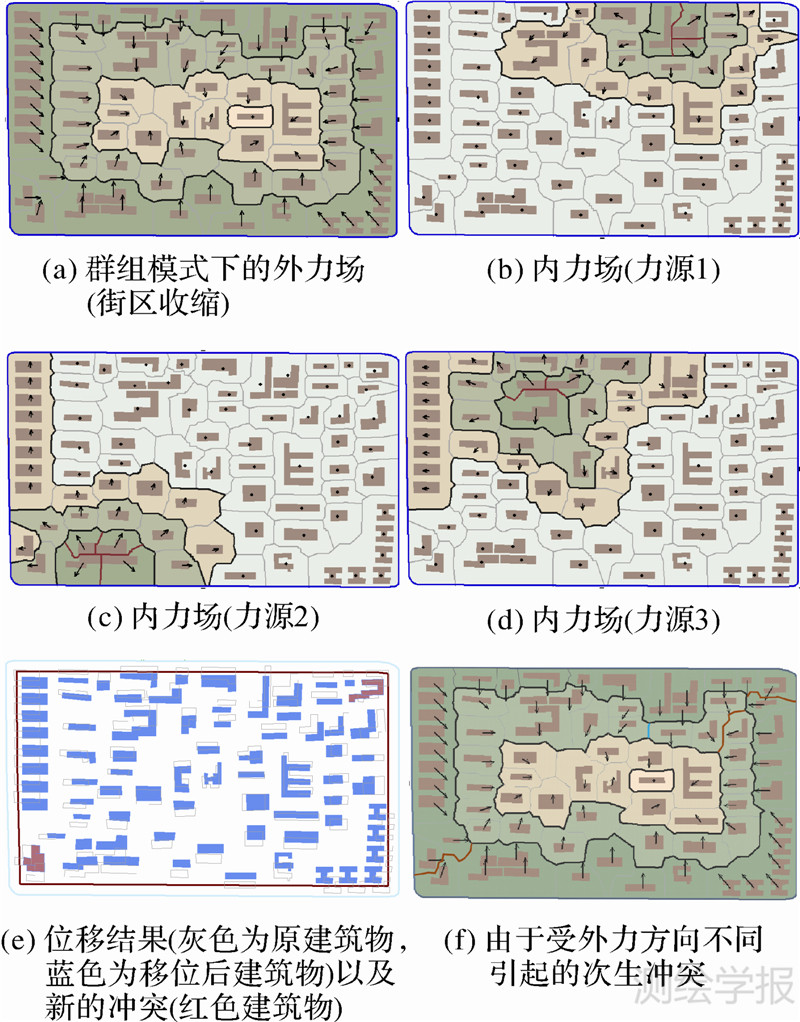
|
| 图 3 多力源移位场模型示意图 Fig. 3 The multi-source force field model |
每个建筑物受到外力的挤压,同时受到不同内部空间冲突的内力排斥,其最终的位置通过多个力的合力作用决定,依据向量和的平行四边形原则计算每个建筑物目标获得的多个力的合力,得到最终建筑物移动的方向和偏移量(图 3(e))。
利用通视距离探冲突并引入内力场可以消除因为外力挤压大小不同产生的次生冲突。而不同方向的外力也会导致空间目标的次生冲突,这种情况在街区转角处多有发生。根据邻近空间目标外力方向的差异,可以在冲突区域引入新的斥力发生源(图 3(f)红色边界)或引力发生源(图 3(f)蓝色边界)作为内力源以建立内力场,使得这种差异可以平均地分散到邻近空间目标,减少冲突的可能性并保持相对空间位置。引入内力场进行移位不能完全避免次生空间冲突,同时空间分布模式往往需要精确地保持空间目标的位置,因此,下一章将探讨空间模式的保持与次生冲突的消除。
4 空间模式保持与次生冲突消除保持空间群目标的分布模式是进行地图综合过程中一个重要的约束,分布模式主要指空间数据中重复出现的一些特征,如:形状、方向、连通性、密度和分布等特征[17]。建筑群的分布模式反映了特定时期的建筑风格。在尺度变换后同一模式下的目标组应以一个整体保持。在移位场模型中,分布模式相同的空间目标被当成一个完整的群组进行分析。在建立移位场模型之前,需要先识别出空间群目标中的完整模式。空间群目标分布模式有多种形式,包括阵列式、直线式、弧线式等[18, 19, 20]。关于如何识别多边形群空间分布模式超出了本文的研究范围,这里利用文献[18, 19, 20]的研究成果将识别的结果应用到移位场模型,改进移位场对空间的剖分。
同一分布模式的空间群目标的分布特征具有规则性,在利用移位场模型进行移位的时候容易受到不同大小和方向的力而破坏其规则性。在移位场模型中将其作为一个整体来分析它们在移位场中的受力情况,从而在移位过程中使得它们具有相同的偏移量,最终保持空间目标的分布模式。实现的方法是,对原Voronoi剖分结果重新处理,删除同一模式下的空间目标之间的公共剖分边(图 2中A、B区域内的灰色边),对这些空间目标以单个空间目标的方式分析受力并计算偏移量,利用偏移量对这些空间目标进行移位。
图 2中A、B区域分别为识别出的直线分布和曲线分布,在构建移位场的时候把A、B区域分别作为一个整体对待。同时在计算其受到的外力(图 3(a))和内力(图 3(b)、(c)、(d))时都将其当作一个整体对待。从图 3(f)可以看出,进行移位时群组内部的所有空间目标都具有相同的偏移量,移位后保持了原有的形态模式。
对图 3(f)分析可以发现通过冲突检测并引入内力场可以有效地避免绝大部分次生冲突,但个别次生冲突由于目标受到不同方向的作用力而出现。为了解决这个问题,本文采用后处理的方法,即在利用多力源移位场模型对空间目标群进行移位之后,检查空间目标是否出现重叠确定次生冲突区域(图 3(f)中的红色建筑物),对次生冲突区域的空间目标附加单独的作用力(图 4(a))进行移位而解决冲突。这个力的大小与冲突区域面积成正比,力的方向与冲突目标之间的邻近关系线的法线方向相同。
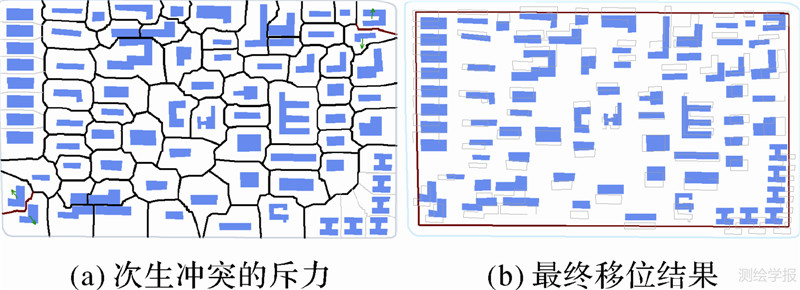
|
| 图 4 次生冲突斥力引入以及最终移位结果 Fig. 4 New conflict detection and resolution |
从最终移位结果(图 4(b))中可以看出,本模型有效避免了次生冲突、保持了目标群的形态模式。移位操作保持形态模式且避免次生冲突后,评价其好坏最关键的是相对位置关系的保持状况,即移位后能够良好地保持空间目标的密度对比关系。空间目标在Voronoi图中对应的剖分结构体现了其影响范围,通过对比移位前后影响区域面积可以考察相对位置关系的保持状况,进而评价移位效果。图 5(a)、图 5(b)分别为试验中移位前后建筑物影响区域。在图 5(c)中横坐标、纵坐标分别为为移位前、后各建筑物影响区域的面积,通过直线拟合得到横纵坐标的关系为:y=0.861x,其确定系数(R2)为0.883 9,说明移位前后影响区域的面积高度相关;另外通过统计计算得到影响区域前后面积比的平均值为86.1%、标准差为0.125,同样也说明了位移前后建筑物影响区域面积比值集中分布在86.1%附近(图 5(d)),从定量分析说明本模型良好地保持了空间目标的分布密度,维持了空间目标的相对位置关系。
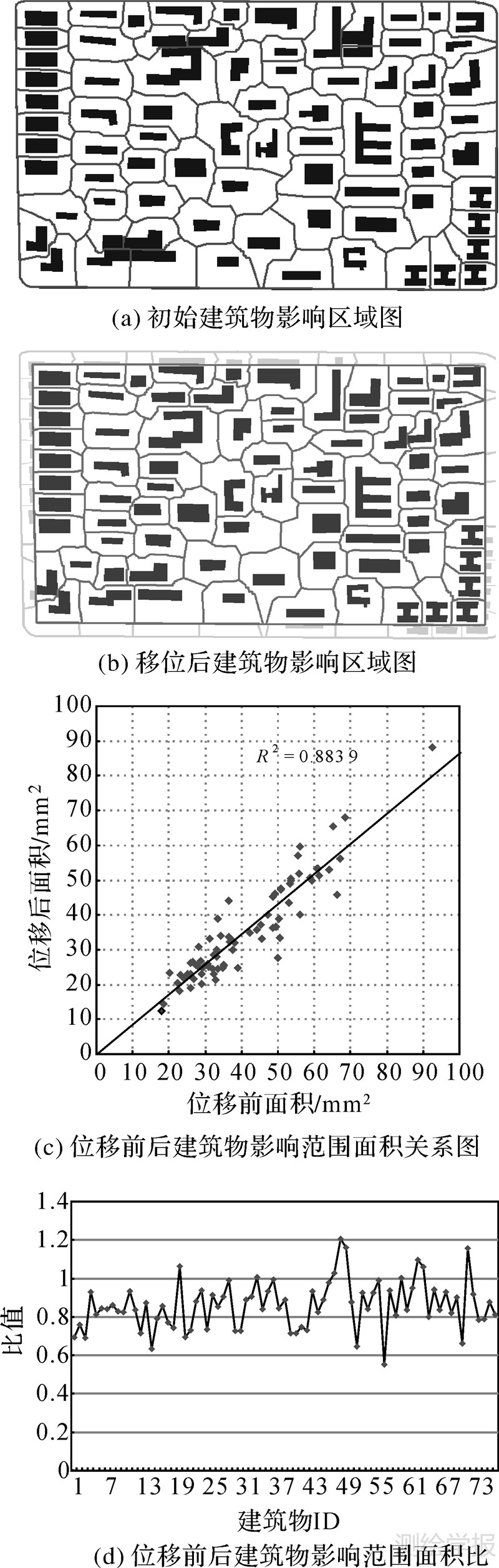
|
| 图 5 综合评价结果 Fig. 5 Numerical evaluation |
制图综合中的移位需要保持其空间分布模式同时避免空间目标之间的冲突,本研究借鉴“场论”的思想,将空间群目标作为一个整体,利用Voronoi图的空间剖分几何构造模拟空间目标场。引入外部挤压产生的对目标群的外力,通过邻近距离阈值探测空间冲突作为内力发生源而引入内力。外力与内力在空间场中逐级衰减传递以确定其强度与方向,同时探测并顾及空间目标的分布模式,最后通过计算外力与内力的矢量和得到每个空间目标最终移位的方向与偏移距离,建立了多力源作用下的移位场模型,该方法比较好地将多种空间冲突一次性集成考虑,避免顾此失彼,较好地保持空间目标的局部分布模式与整体分布特征,实现了满足以上条件的制图综合自动移位。
本模型与基于优化技术的移位算法相比,避免了多次迭代求取最优解,同时在计算过程中充分利用多边形目标的Voronoi图剖分结构,提高了运算效率,同时也避免多次迭代中导致空间目标的分布模式被破坏,适用于解决空间群目标在尺度变化中的空间冲突问题。当目标区域过于密集,应该结合其他综合操作如选取、合并、旋转解决空间冲突。本模型将空间目标作为最小操作单元,因此无法处理需要对空间目标进行局部移位的情况,如道路或河流需要对其中一段进行移位。
本文提出的面向多重空间冲突解决的移位场模型在实际应用当中可以结合具体情况作以下扩展:① 本模型可作为其他操作的后处理,例如对空间群目标中某个目标夸大后,将其作为新的斥力发生源引入本模型从而解决因夸大产生的冲突;② 本研究建立的Voronoi图剖分结构可以作为其他综合操作的支持,例如多边形聚类、多边形合并等综合操作也需要利用Voronoi图剖分结构;③ 在本模型中引入引力以保持空间目标的相对位置关系,例如在对道路进行化简后,会导致两侧的空间目标远离道路,此时可以引入道路对空间目标的引力,以保持它们的相对位置关系。
| [1] | TOPFER F.Cartographic Generalization[M]. Translated by JIANG Anning.Beijing:Surveying and Mapping Press,1982:152.(特普费尔.制图综合[M].江安宁,译.北京:测绘出版社,1982:152.) |
| [2] | PAUL A, MICHAEL F, GOODCHILD,et al.Geographical Information System-Principles,Techniques,Management and Application[M].New York:John Wiley,1999:125-155. |
| [3] | RUAS A.A Method for Building Displacement in Automated Map Generalisation[J].International Journal of Geographic Information Science,1998,12(7):789-803. |
| [4] | JONES C B,BUNDY G L,WARE J M.Map Generalization with a Triangulated Data Structure[J]. Cartography and GIS,1995,22( 4) :317- 331. |
| [5] | WU Xiaofang, DU Qingyun, XU Zhiyong. Disposal of Spatial Conflict between Roads and Buildings Based on the Multilevel Displacement Principles[J].Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 649-654. ( 吴小芳, 杜清运, 徐智勇.多层次移位原则的道路与建筑物空间冲突处理[J].测绘学报,2010,39(6):649-654.) |
| [6] | AI Tinghua. A Displacement of Building Cluster Based on Field Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 89-94. (艾廷华.基于场论分析的建筑物群的移位[J].测绘学报,2004,33(1):89-94.) |
| [7] | WARE J M,JONES C B. Confiict Reduction in Map Generaiization Using Iterative Improvement[J]. Geoinformatica,1998,2(4):383-407. |
| [8] | WARE J M,THOMAS N,JONES C B. Resolving Graphic Conflict in Scale Reduced Maps: Refining the Simulated Annealing Technique[C]//Proceedings of 5th Workshop on Progress in Automated Map Generalization.[S.l.]: ICA Commission on Map Generalization,2003. |
| [9] | WILSON I D, WARE J M, WARE J A. Reducing Graphic Conflict in Scale Reduced Maps Using a Genetic Algorithm[C]//Proceedings of 5th Workshop on Progress in Automated Map Generalization. [S.l.]: ICA Commission on Map Generalization,2003. |
| [10] | HARRIE L. The Constraint Method for Solving Spatial Conflicts in Cartographic Generalization[J]. Cartography and Geographic Information Science,1999,26(1):55-69. |
| [11] | HARRIE L,SARJAKOSKI T. Simultaneous Graphic Generalization of Vector Data Sets[J]. GeoInformatica,2002,6(3):233-261. |
| [12] | HGJJHOLT P. Solving Space Conflicts in Map Generalization:Using a Finite Element Method[J]. Cartography and GIS,2000,27(1):65-73. |
| [13] | BADER M,BARRAULT M,WEIBEL R. Building Displacement over a Ductile Truss[J]. International Journal of Geographical Information Science,2005,19(8-9):915-936. |
| [14] | WU Fang, HOU Xuan, QIAN Haizhong, et al. A Model for Road Network Displacement in Automated Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3):262-268. (武芳,侯璇,钱海忠,等. 自动制图综合中的线目标位移模型[J]. 测绘学报,2005,34(3):262-268.) |
| [15] | AI Tinghua,GUO Renzhong. Extracting Centerline and Building Street Network Based on Constrained Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica,2000,29(4):348-354.(艾廷华,郭仁忠. 基于约束Delaunay 结构的街道中轴线提取及网络模型建立[J]. 测绘学报,2000,29(4):348-354.) |
| [16] | AI Tinghua,GUO Renzhong. Polygon Cluster Pattern Mining Based on Gestalt Principles[J]. Acta Geodaetica et Cartographica Sinica,2007,36 (3):302-308.(艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报,2007,36 (3):302-308.) |
| [17] | MACKANESS W, EDWARDS G.The Importance of Modeling Pattern and Structure in Automated Map Generalization[C]//Proceedings of Joint Workshop on Multi-Scale Representations of Spatial Data. Ottawa:[s.n.], 2002. |
| [18] | REGNAULD N. Recognition of Building Cluster for Generalization[C]//Proceedings of the 7th International Symposium on Spatial Data Handling. Coimbra:[s.n.], 1996:85-198. |
| [19] | REGNAULD N. Contextual Building Typification in Automated Map Generalization[J].Algorithmica, 2001, 30(2):312-333. |
| [20] | ZHANG Xiang,AI Tinghua, STOTER J,et al. Building Pattern Recognition in Topographic Data: Examples on Collinear and Curvilinear Alignments[J]. Geoinformatica,2013, 17(1): 1-33. |


