近年来精密单点定位[1, 2, 3](precise point positioning,PPP)固定解已成为GPS领域的研究热点与前沿之一[4, 5, 6, 7, 8, 9, 10, 11]。国内外学者相继提出了星间单差和非差模型的分离相位小数周偏差(fractional cycle bias,FCB)的方法[4, 5]以及非差模型的整数卫星钟差方法[8, 9](integer-recovery clock,IRC)。以上两类方法理论上具有等价性,其关键都在于通过GPS观测网的数据分离出FCB,生成高精度的“整数卫星产品”恢复非差或星间单差模糊度的整数特性[10]。该FCB由接收机和卫星端未检校的硬件延迟引起[12]。在传统PPP浮点解模型中,FCB与整周模糊度参数难以有效分离,将两者作为整体进行估计。FCB不会影响传统的PPP浮点解精度,但破坏了模糊度参数的整数特性,使得传统模型无法利用其整数特性,其解算精度及可靠性较双差解略差。而对于PPP固定解,FCB的精度会影响模糊度固定的正确与否。目前FCB方法分别生成宽巷和窄巷FCB改正文件;IRC方法也分别提供宽巷FCB和保持L1模糊度整数特性的卫星钟差文件,服务于PPP模糊度固定。因此就本文关注的PPP固定解来说,无论是FCB还是IRC方法,获得稳定、可靠的卫星宽巷FCB产品,正确固定宽巷模糊度是实现PPP固定解的重要前提条件。
为估计高精度的卫星端FCB产品,文献[12]最早对FCB的时间稳定性进行了研究,指出其稳定度优于1ns。文献[13]的试验结果表明每天一组的星间单差宽巷FCB在数月内都保持稳定。文献[4]通过取平均的方法估计任意卫星对的单差FCB。其试验结果表明卫星端宽巷FCB在数天内的变化小于0.05周。上述研究证实了卫星端的宽巷FCB具有长期稳定性,估计星间单差宽巷FCB时可以无需考虑接收机端FCB的处理。
另一方面,在IRC方法中,文献[4, 5]等基于单天内接收机端宽巷FCB足够稳定(变化小于0.1周)的假设,选定某一接收机宽巷FCB作为基准,使用序贯最小二乘法估计每天一组卫星端与接收机端宽巷FCB。然而他们并未对接收机端宽巷FCB的时变性质进行分析,该方法的假设前提是否可靠还需进一步研究。实际上,接收机端宽巷FCB的稳定性不仅与接收机的硬件相关,还取决于其工作状态等众多影响因素[10, 12]。接收机端的宽巷FCB是否具有稳定性,目前还鲜有文献论述。因此,本文试图从计算宽巷FCB的基本原理出发,通过大量的数据从不同角度来深入分析接收机端与卫星端宽巷FCB的时变特征,检验文献[4, 5]等方法的前提假设是否准确,论证其估计非差宽巷FCB方法是否严密,为估计高精度非差宽巷FCB提供合理的建议。
2 宽巷FCB考虑接收机端与卫星端FCB,GPS相位L和伪距P的原始观测方程可表示为[11, 14]
式中,j代表信号频率;r为接收机;s为卫星;i代表历元;P为伪距观测值;Φ为载波相位观测值;ρ为接收机与卫星天线相位中心的距离,包括固体潮、海洋潮和相对论效应的影响;c为光速;dtr为接收机钟偏差;dts是卫星钟差;T是对流层延迟量;λ为载波波长;N为整周模糊度;br,j为接收机码偏差;bs,j为卫星端码偏差;Φr,j是接收机端相位偏差;Φs,j为卫星端相位偏差;Isr,1(i)表示L1频率视线方向的电离层群延迟;uj=λ2j/λ21。
依据上式使用Melbourne-Wübbena (MW)组合[15, 16]计算出宽巷浮点模糊度的估值如下
式中,Ñ w为MW组合计算得到的实数宽巷模糊度,Nw为实际的宽巷整周模糊度,fi、fk分别为接收机端与卫星端的宽巷FCB[6, 7, 10]。该组合观测值消除了电离层、卫星与接收机钟差项等影响,具有较长的波长(0.86m),能较为准确估计宽巷模糊度[17, 18]。由于伪距测量的噪声较大,需要对无周跳弧段内的数据进行平滑以获得较为准确的实数宽巷模糊度估值。通过对弧段内取平均得到 式中,〈 〉表示取平均。式(6)表明由于受接收机端与卫星端宽巷FCB的影响,使得计算出的宽巷模糊度失去了整数特性。该卫星端和接收机端的FCB可通过站星间双差予以消除,不会影响双差模糊度固定。对于PPP用户来说,如果能事先确定卫星端的宽巷FCB值fk,在定位时就可以利用fk去改正MW组合观测值,恢复宽巷模糊度的整数特性。其中接收机端宽巷FCB可通过在星间求差消除或是在非差模型用接收机钟差来吸收。因此,为固定宽巷模糊度,可利用全球或区域IGS跟踪站的观测数据先估计出卫星端宽巷FCB值,然后将卫星端宽巷FCB播发给PPP用户使用。 3 非差FCB估计对服务端观测网络每一个测站-卫星弧段,将式(6)改写成如下形式
式中,Rki为宽巷模糊度估值〈w〉的小数部分;fi和fk分别为接收机端与卫星端宽巷FCB。在IRC方法中文献[4, 5]等使用序贯最小二乘法估计非差卫星端宽巷FCB[8]。其具体算法流程为:首先在数据预处理过程中,通过加1周或减1周操作调整Rki值以保证相同测站-卫星对之间的宽巷FCB的连续性(在Rki接近0或1的情况下,如Rki多个取值分别为0.98、0.95、0.01时,0.01需要加1调整)。同时,剔除相同测站-卫星对不同弧段的数据间存在的粗差。从上述公式出发,选取某个测站i0的接收机端FCB 1 fi0 作为基准,将其固定为0,消除由式(7)联立形成的方程组的秩亏。在第一轮处理中估计1 fi 和1 fk的初值,同时进一步调整Rki值消除不同测站同一卫星对间可能存在的不连续性,最终固定所有Rki。最后使用最小二乘估计出所有测站与接收机端宽巷FCB。
该方法无需在星间作差,为消除方程组中的秩亏,选取某一接收机宽巷FCB为0,直接估计出每天一组非差宽巷FCB。实际假定了单天内接收机与卫星端宽巷FCB均足够稳定(文献[4, 5]认为其变化小于0.1周)。但是,关于接收机端宽巷FCB稳定性,还鲜有文献论述。因而文献[4, 5]给出的上述方法的前提假设成立与否还需要深入研究。此外,为得到精度较高的宽巷模糊度估值小数部分历元平滑结果Rki,文献[4, 5]等也没有给出可供参考的计算宽巷FCB的最短弧段长度阈值。
4 宽巷FCB时变特性分析 4.1 试验方案为分析宽巷FCB的时变特性,论证文献[4, 5]依据的前提假设是否严密,本文选取2009-12-27—2010-01-05共10 d全球350个IGS跟踪站[19]的大量GPS观测数据进行试验,截止高度角设置为10°。数据预处理阶段首先进行钟跳探测与修复,避免将接收机钟跳引起的观测值跳变误判为周跳[20, 21]。然后联合使用geometry-free(GF)与MW组合进行周跳探测[22],同时输出单历元非差宽巷FCB以及无周跳弧段内逐历元平滑后的宽巷FCB用于试验分析。
4.2 非差站星宽巷FCB序列分析以2010年001天ALGO、NRC1和AJAC站为例(测站的基本信息如表 1所示),图 1~3中给出了部分卫星在未发生周跳的弧度内非差FCB单历元结果与逐历元平滑结果。其他未绘图卫星的时间序列与之相似。图中每个弧段的时间长度约为6h,其中“GXX_0”表示PRN为XX卫星单历元结果,“GXX_1”为相应卫星的逐历元平滑结果。为方便绘图,部分卫星的FCB加/减某一整数值以便在图中与其他卫星区分开。
| 测站 | 纬度 | 经度 | 地区 | 接收机类型 |
| ALGO | 46.0° | -78.1° | Canada | AOA BENCHMARK ACT |
| NRC1 | 45.5° | -75.6° | Canada | ASHTECH Z-XII3T |
| AJAC | 41.9° | 8.8° | France | LEICA GRX1200GGPRO |
从图 1~3可以看出,站星间宽巷FCB的单历元系列基本表现为均值为一常数的平稳随机量,在高度角较低(约低于15°)的情况下,由于受观测噪声以及多路径效应的影响,序列噪声较大。噪声最小的AJAC站波动范围接近1周;最大的NRC1站波动范围则几乎接近3周。在低高度角情况下测站的观测噪声各不相同,这可能与接收机质量或具体观测环境有关。随着卫星高度角的升高,宽巷FCB序列噪声明显减小,ALGO和AJAC站时序变化小于0.5周,NRC1站在0.5周左右。
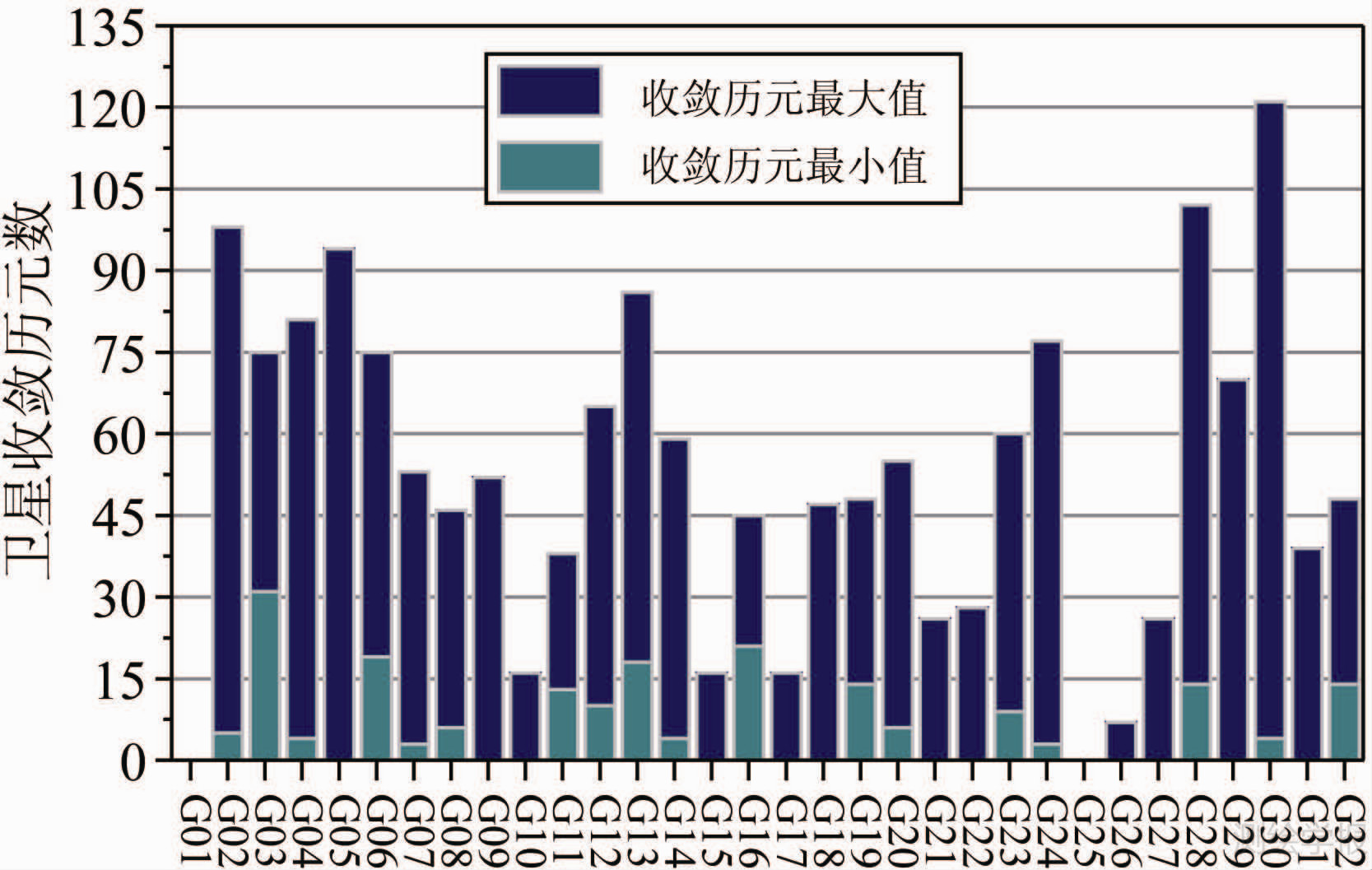
从图 1~3中的逐历元平滑结果来看,非差FCB在经过一段时间平滑“初始化”后即接近一条稳定的水平直线,显著削弱了伪距观测噪声对FCB估值的影响。笔者将所有历元最终平滑值作为参考,统计历元平滑结果达到0.1周精度所需的历元数(其中AJAC站G12和G29卫星存在数据中断,统计的是较长时间段的数据)。对于图中3个测站共16颗卫星,多数卫星经过40个历元(20min)平滑以后即可收敛到0.1周精度,最快为ALGO站G31卫星第一个历元开始的结果即收敛,最慢为ALGO站G28卫星需要74个历元。收敛所需历元数的多少主要与低高度角情况下的观测数据质量有关。对这3个测站进一步统计了所有卫星收敛历元数的最大最小值,如图 4所示。可以看出除了G02、G05、G28和G30卫星外,其他卫星最长收敛时间均不超过90个历元(45min)。而在大部分情况下这4颗卫星经过90个历元(45min)的平滑也能收敛到0.1周以内的精度。据此为了计算较高精度的非差宽巷FCB,本文建议数据的观测时间应不少于45min。

|
| 图 1 ALGO站单天非差宽巷FCB时间序列 Fig. 1 The daily undifferenced wide-lane FCB time series of ALGO |

|
| 图 2 NRC1站单天非差宽巷FCB时间序列 Fig. 2 The daily undifferenced wide-lane FCB time series of NRC1 |

|
| 图 3 AJAC站单天非差宽巷FCB时间序列 Fig. 3 The daily undifferenced wide-lane FCB time series of AJAC |
|
| 图 4 3个测站非差宽巷模糊度收敛历元数最大最小值 Fig. 4 The maximum and minimum number of convergence epoch of undifferenced wide-lane ambiguities at 3 stations |
值得注意的是图 3中,AJAC站G12与G29卫星宽巷FCB序列存在明显的分段现象(其他卫星均有明显分段现象),段内稳定性较好,而段与段之间有明显的跳跃,且两颗卫星的跳变值较为接近。检查该站原始观测文件,发现在06h 25m 30s与06h 28m 30s之间数据中断,重新观测后所有卫星载波相位发生周跳。而对比数据中断前后的历元平滑结果发现,两颗卫星fi-fk的跳变值均约为0.4周。由于卫星端保持连续正常工作,并未发生异常,因此推断出图 3中的跳跃现象是由AJAC站接收机重启所致。这说明接收机重启会使接收机端FCB重新赋值。这在现有的关于FCB估计的研究中是未被考虑到的。对于重新启动的接收机观测数据,在序贯最小二乘方法中必须增加新的接收机宽巷FCB参数以保证估值精度和可靠性。
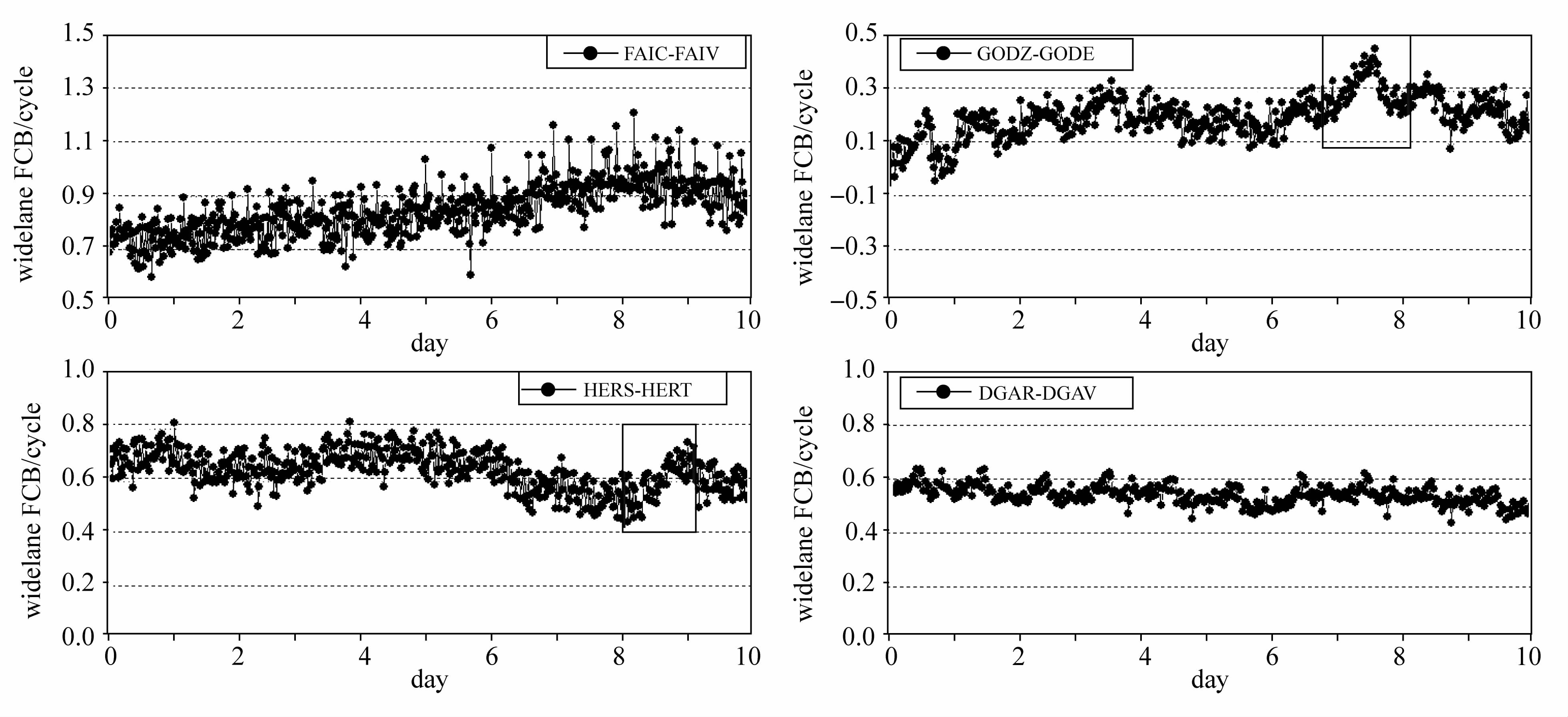
4.3 站间差宽巷FCB序列分析这里将两个测站相同卫星重叠时间在1h以上的非差宽巷FCB进行站间差分,以消除卫星端FCB的影响。随机选取4对短基线测站(FAIC-FAIV、GODZ-GODE、HERS-HERT、DGAR-DGAV),其信息如表 2所示。按时间顺序给出其10d内站间差FCB的序列,如图 5所示。从图 5可以看出,DGAR-DGAV站间差宽巷FCB在10d范围内都比较稳定,所有数据变化范围小于0.15周。FAIC-FAIV站间差宽巷FCB稳定性稍差,其在10d内的变化幅度约为0.25周。其余两组结果稳定性相对更差,10d内的变化量在0.3周左右。这说明接收机端宽巷FCB的长期稳定性与卫星端相比较差。此外,图中矩形分别标注的是GODZ-GODE第7天的站间差FCB和HERS-HERT第8天的站间差FCB结果。此两段数据站间差宽巷FCB时间序列变化较为剧烈,其单天内变化量即接近0.3周,远大于文献[4, 5]假定的小于0.1周的变化量。
|
| 图 5 4对短基线10d的站间差FCB序列 Fig. 5 The 10 day’s single-difference-between-station FCB time series of four short baselines |
| 测站对 | 纬度 | 经度 | 地区 | 接收机类型 |
| FAIC-FAIV | 65.0° | -147.5° | USA | TRIMBLE NETRS/JPS EGGDT |
| GODZ-GODE | 39.0° | -76.8° | USA | JPS EGGDT/ASHTECH UZ-12 |
| HERS-HERT | 50.9° | 0.3° | U.K. | ASHTECH Z-XII3/LEICA GRX1200GGPRO |
| DGAR-DGAV | -7.3° | 72.4° | U.K. | ASHTECH UZ-12/JPS EGGDT |
上述结果表明不同接收机的宽巷FCB稳定性不同,单天内接收机端宽巷FCB并非稳定不变的值,其在不同的天内随时间变化速率不一样,一天内最大变化量可以达到0.3周。因此,简单假定接收机宽巷FCB在一天内稳定并不可靠。
4.4 讨论与分析在IRC方法中,文献[4, 5]等基于单天内接收机端宽巷FCB足够稳定(变化小于0.1周)的假设,选定某一接收机宽巷FCB作为基准,使用序贯最小二乘法估计每天一组卫星端与接收机端宽巷FCB,但并未对该前提假设进行细致研究。结合本文的试验可知,该假设前提并不可靠。首先,接收机重启会使接收机端宽巷FCB重新赋值。重启前后其变化达到0.4周。这在现有的关于FCB估计的研究中是未被考虑到的。其次,不同接收机的宽巷FCB稳定性不同。单天内接收机端宽巷FCB也并非稳定不变的值,其在不同的单日内随时间变化速率不一样,一天内最大变化量可以达到0.3周。
由于文献[4, 5]等将单天的接收机FCB作为一个时不变参数进行估计,其变化量将会被卫星端FCB吸收,势必会影响FCB估计的精度。虽然该方法基于一定的质量控制策略能够减弱不合理假设带来的影响,但也增加了数据剔除率,未能充分利用可用的观测信息。为了避免上述不利影响,获得更高精度的非差宽巷FCB估值,对于接收机重新启动的观测数据,需要新增一个接收机FCB参数;而对于接收机FCB的时变特性,可以在估计时将其作为随机游走过程进行估计。
5 结论与展望笔者对IRC方法中估计非差宽巷FCB的序贯最小二乘方法进行了论述,指出其不足在于事先假定了单天内的(接收机端和卫星端)宽巷FCB稳定不变,而对其时变性质缺少讨论与分析。本文处理了2009-12-27—2010-01-05共10d全球350个IGS测站的GPS观测数据,从站星非差宽巷FCB、站间单差宽巷FCB序列两方面对接收机端宽巷FCB的时变特性进行了详细的分析和讨论。得出如下结论:
(1) 在没有周跳的连续弧段内宽巷FCB序列具有较好的稳定性。使用不少于90个历元(45min)的数据进行平滑即可以使宽巷FCB结果收敛到0.1周以内,并且保持精度稳定,继续增加观测历元对宽巷FCB结果影响很小。根据该结论,本文建议估计宽巷FCB的最短弧段不应少于45min。
(2) 单天内接收机端宽巷FCB并非稳定不变的值,其在不同的单日内随时间变化速率不一样,一天内最大变化量可以达到0.4周。因此简单假定接收机宽巷FCB在一天内稳定并不可靠。并且接收机重启会使其重新赋值,破坏FCB值的稳定性。
本文关于接收机端宽巷FCB时变特性的分析表明文献[4, 5]等的序贯最小二乘法所依据的假设前提并不可靠,为获得更高精度的非差卫星宽巷FCB估值,对于接收机重新启动的观测数据,需要新增一个接收机FCB参数;而对于接收机FCB的时变特性,可以在估计时将其作为随机游走过程进行估计。
基于本文的研究成果,在下一步的研究中期望利用更长时间的数据(如几个月甚至一年)进行接收机端宽巷FCB变化规律的分析与建模。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. |
| [2] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica Cartographica Sinica, 2010, 39(5): 478-483. (张宝成,欧吉坤,袁运斌,等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报,2010, 39(5): 478-483.) |
| [3] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver’s Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica Cartographica Sinica, 2011, 40(4): 447-453. (张宝成,欧吉坤,袁运斌,等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453.) |
| [4] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning(PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. |
| [5] | GENG J, TEFERLE F N, SHI C, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solution, 2009, 13(4): 263-270. |
| [6] | ZHANG Xiaohong, LI Xingxing. A New Method for Zero-differenced Integer Ambiguity Resolution and Its Application to PPP[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 657-660. (张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报: 信息科学版, 2010, 35(6): 657-660.) |
| [7] | LI Xingxing, ZHANG Xiaohong, LI Pan. PPP for Rapid Precise Positioning and Orbit Determination with Zero-difference Integer Ambiguity Fixing[J]. Chinese Journal of Geophysical, 2012, 55(3): 833-840. (李星星, 张小红, 李盼. 固定非差整数模糊度的PPP快速精密定位定轨[J]. 地球物理学报, 2012, 55(3): 833-840.) |
| [8] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation Journal of Institute of Navigation, 2009, 56(2):135-149. |
| [9] | LAURICHESSE D. The CNES Real-time PPP with Undifferenced Integer Ambiguity Resolution Demonstrator[C]//Proceedings of the ION GNSS 2011. Portland: [s.n.], 2011. |
| [10] | GENG J H, MENG X L, DODSON A, et al. Integer Ambiguity Resolution in Precise Point Positioning: Method Comparison[J]. Journal of Geodesy, 2010, 64(9): 569-581. |
| [11] | ZHANG Baocheng, OU Jikun. On the Different Strategies for Integer Ambiguity Resolution in Precise Point Positioning[J]. Acta Geodaetica Cartographica Sinica, 2011, 40(6): 710-716. (张宝成, 欧吉坤. 论精密单点定位整周模糊度解算的不同策略[J]. 测绘学报, 2011, 40(6): 710-716.) |
| [12] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000km[J]. Journal of Geophysical Research, 1989, 94(B8): 10187-10203. |
| [13] | GABOR M J, NEREM R S. GPS Carrier Phase Ambiguity Resolution Using Satellite-satellite Single Difference[C]//Proceedings of ION GNSS 12th International Technical Meeting of the Satellite Division. Nashville: [s.n.], 1999: 1569-1578. |
| [14] | TEUNISSEN P J G, KLEUSBERG A. GPS for Geodesy[M]. New York: Springer, 2009. |
| [15] | Melbourne W G. The Case for Ranging in GPS-based Geodetic Systems[C]//Proceedings of First International Symposium on Precise Positioning with the Global Positioning System. Rockville: [s.n.], 1985: 373-386. |
| [16] | WVBBENA G. Software Developments for Geodetic Positioning with GPS Using TI-4100 Code and Carrier Measurements[C]//Proceedings of First International Symposium on Precise Positioning with the Global Positioning System. Rockville: [s.n.], 1985: 403-412. |
| [17] | ZHU Huizhong, LIU Jingnan, TANG Weiming, et al. The Algorithm of Single-epoch Integer Ambiguity Resolution between Long-range Network RTK Base Stations[J]. Acta Geodaetica Cartographica Sinica, 2012, 41(3): 359-365. (祝会忠,刘经南,唐卫明,等. 长距离网络RTK基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3): 359-365.) |
| [18] | ZHOU Letao, HUANG Dingfa, YUAN Linguo, et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica Cartographica Sinica, 2007, 36(1): 37-42. (周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(1): 37-42.) |
| [19] | JIAO Wen hai, WANG Gang, JIA Xiaolin. Combination Analysis of Global IGS Network and Regional GPS Network[J]. Acta Geodaetica Cartographica Sinica, 2000, 29(S1): 90-95. (焦文海, 王刚, 贾小林. 全球IGS站数据与GPS区域网数据的联合处理[J].测绘学报, 2000, 29(S1): 90-95.) |
| [20] | ZHANG Xiaohong, GUO Fei, LI Pan, et al. Real-time Control Procedure for GNSS Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 940-944. (张小红, 郭斐, 李盼, 等. GNSS精密单点定位中的实时质量控制[J]. 武汉大学学报: 信息科学版, 2012, 37(8): 940-944.) |
| [21] | KIM D, LANGLEY R B. Quality Control Techniques and Issues in GPS Applications: Stochastic Modeling and Reliability Test[C]//Proceedings of the 2001 International Symposium on GPS/GNSS. Jeju Island: [s.n.], 2001. |
| [22] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. |