2. 安徽大学 资源与环境工程学院,安徽 合肥 230601
2. School of Resources and Environment Engineering,Anhui University,Hefei 230601,China
面状要素的骨架线是对面状地物主体形状的抽象描述,它反映了面状地物的主延伸方向和主体形状特征,在GIS中有着非常重要的应用,如在制图综合中双线河流的简化、面状地物注记的自动配置、多边形合并及其他空间分析[1]。此外,栅格骨架线还可以用于栅格数据的压缩[2]。
面状要素骨架线的提取算法通常有基于矢量方式和栅格方式两类方法。其中基于矢量方式的代表算法有平行线切割中点连线法[3]、Delaunay三角网法[4, 5]、Voronoi图法[6, 7, 8, 9]和曲率计算法[10]等。平行线切割中点连线法是最简单、最直观的求取骨架线的方法,但是它只能处理一些简单的多边形,对于复杂的多边形(如有岛多边形),处理起来比较困难。Delaunay三角网法的基本原理是:通过对多边形边界上的离散特征点建立Delaunay三角网,并连接各相邻的三角形外接圆圆心(或内接圆圆心)作为多边形的骨架线。该法仅能得到近似骨架线,并且,当应用于平行的轮廓如街道,所得到的中轴线存在很多“锯齿”[11]。基于Voronoi图的骨架线提取法主要利用的是Voronoi图与中轴之间的密切关系[12],即多边形边界的Voronoi图界线即为到不同边界元素等距点的轨迹。文献[12]论证了二维Voronoi图和骨架线(中轴线)的各自特征,并给出了二者在凸多边形、简单多边形等不同情况下的相互关系及证明。Voronoi图法与中轴的最大不同在于:Voronoi法中,多边形边界的划定将直接影响到骨架线提取;中轴线则是边界元素的内接圆的圆心轨迹,中轴线的构建对于边界元素的分段的变化不敏感,仅依赖于边界元素的几何形状。当Voronoi法应用于完全由直线段构成的凸多边形时,由于其边界划定明确、且往往与边界元素的图形几何形态一致,此时的多边形边界Voronoi图界线与中轴(骨架线)是完全相等的[12]。对于含复杂曲边、边界划分不明确的多边形,如何合理划分多边形边界是该类方法的关键和难点[7, 13]。曲率计算法是利用几何学原理设计的算法,由于无限曲率的存在,容易导致所提取的骨架线与原图形存在拓扑不同构。基于栅格方式的方法包括用距离变换法搜寻中轴线法[14, 15]、经典细化算法[16]、边缘跟踪剥皮法[17]、数学形态学方法[2]等。基于栅格的骨架线提取方法具有处理数据速度快、内存需求少和适应性强的优点。此外,还有其他算法,例如改进的Douglas-Peucker算法[18]、基于内侧缓冲区算法[19],通过对不规则多边形进行三角切割的多边形骨架线的方法[20]。
现有的骨架线提取方法各有优点,但存在的普遍问题有:① 骨架线未能延长到边[10, 16];② 所提取的骨架线与原图形存在拓扑不同构[10];③ 所提取的骨架线含有许多不必要的分支,即有毛刺[21],难以根据需要只提取主骨架线[6, 16];④ 难以提取多层次骨架线[10, 20, 21]等。
针对上述问题,本文提出一种面状要素的多层次骨架线提取方法。主要利用双缓冲变换所具有的“保凹”、“保平”、“减凸”特性识别面状要素多边形的弯曲单元,再通过障碍距离变换提取弯曲单元的顶点,并以这些弯曲顶点打断多边形边界,最后通过对分段后的多边形边界线建立Voronoi图,得到面状要素的骨架线。该方法一方面解决了Voronoi图的多边形边界分段难点问题,另一方面可以通过控制双缓冲变换尺度L实现不同级别和密度的骨架线提取,从而得到主次分明的多层次骨架线,符合骨架线所具有的多层次特性。
1 方法原理 1.1 骨架线定义及特性分析所谓骨架线(skeleton),是指用与原形状的连通性和拓扑结构相一致的细曲线作为理想表达的一种对象表示。简单地说,就是位于物体内部的,并能体现其形状特征的简化图形,它具有描述形状凸出的分支部分,也具有描述形状内部空洞的环状部分[22]。物体形态的骨架解释有许多模型,最简单直观的方法是火烧模型[23],常用的描述方法还有距离曲面脊线模型和最大圆盘几何中心模型。
骨架线是图像几何形态的一种重要的拓扑描述,由一些表明物体大致形状的细线组成。利用骨架线表示原始图像,可以在保持图像重要拓扑特征的前提下,减少图像中的冗余信息。在理论和实际应用中,骨架线具有以下特征。
(1) 拓扑一致性[24]:骨架线与原图形形状在拓扑结构上保持一致,它能够反映原图形形状拓扑结构和空间位置的相关信息,二者具有同态等价的关系。
(2) 重建性[23]:骨架线反映了原图形的主延伸方向和主体形状特征,因此,利用骨架线,再结合骨架线到原图形边界的距离,可以实现原始图形的重构。
(3) 对称性[25]:骨架线即中轴线,任意点到原图形两边边界的距离相等。
(4) 层次性:由于图形的形状具有层次结构特征,骨架线的识别与观察尺度有关,在不同尺度下,可以得到不同的骨架线,并且,它们构成层次关系。
1.2 相关变换在此,首先介绍本文方法所涉及的两个主要变换:双缓冲变换和障碍距离变换。
1.2.1 双缓冲变换双缓冲变换是一组综合操作算法,主要包括内、外缓冲变换。即先对原始多边形A(图 1(a))向内进行尺度为L的缓冲变换得到多边形B(图 1(b)),再对多边形B向外进行尺度为L的外缓冲变换得到多边形C(图 1(c)),最后将多边形C与原始多边形A进行叠加,并截取多边形的凸出部分,即弯曲单元(图 1(d))。

|
| 图 1 双缓冲变换分解示意图 Fig. 1 Illustration of double buffering transform |
经过双缓冲变换之后,图形的形态变化具有如下特征:
(1) “保凹”、”保平”、”减凸”,变换前后,总体上图形的大形态不变,及凹陷部分和直线部分的形态无变化,即“保凹”、“保平”。而图形的凸出部分趋于光滑,即“减凸”。
(2) “保凹”、“保平”、“减凸”的程度可控,它由双缓冲变换的宽度L控制。
(3) 由于凹凸相对,改变内外缓冲变换的顺序,可以得到曲线两侧的弯曲单元。
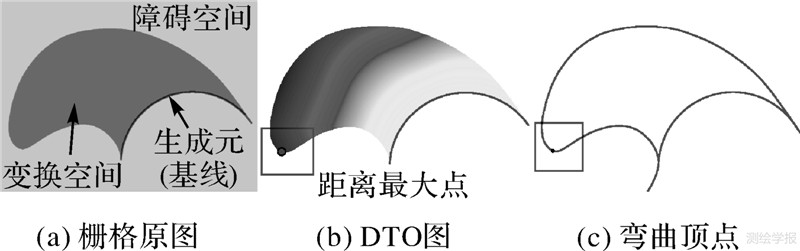
1.2.2 障碍距离变换距离变换的概念首先是由Rosenfeld和Pfalt于1966年引入,它是一种计算并标识各空间像元到最近实体像元的距离的变换。障碍距离变换(distance transformation with obstacles,DTO)是距离变换的一种特殊类型,即在障碍空间中的距离变换,其距离需要绕过障碍物进行传播或累积。目前,DTO生成方法有很多种[26],本文主要利用地图代数DTO生成方法,用来提取弯曲单元的顶点。以弯曲基线为生成元、以弯曲单元内部区域为变换空间、弯曲单元的外部区域为障碍(图 2(a)),进行障碍距离变换(图 2(b)),并提取距离图中距离最大值点,即多边形弯曲单元的顶点(图 2(c))。
|
| 图 2 弯曲顶点的提取 Fig. 2 Extraction of the vertex of the bend |
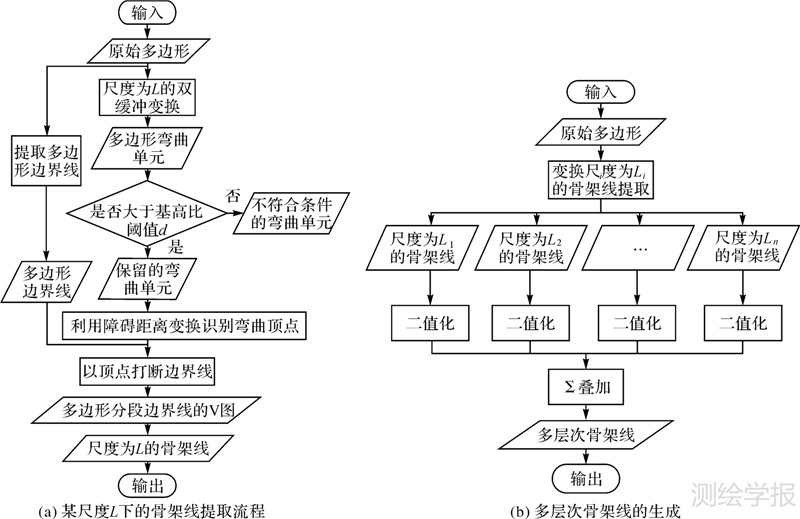
本文方法采用Visual Studio 2008编程和ArcGIS 9.3来实现,主要包括骨架线提取和多层次骨架线结构化两大步骤,如图 3所示。
|
| 图 3 提取多层次骨架线的流程图 Fig. 3 Flow chart of extracting multiscale skeletons for polygonal shapes |
本文方法的核心是某尺度L的多边形骨架线提取。在此,以国家基础地理信息1∶400万湖泊数据中的某一多边形(图 4(a))为例,说明具体的提取步骤:
(1) 对原始多边形进行双缓冲变换,即先对多边形区域进行尺度为L的内缓冲变换,再进行相同尺度的外缓冲变换,将得到的多边形与原始多边形进行裁剪,获得多边形弯曲单元(图 4(b))。
(2) 设置适当的基高比(注:基高比[27]可定义为凸多边形的面积A与多边形凸出线相对的那条边的长度BL的比值,即D=A/BL),并以该基高比剔除狭长弯曲单元,即计算和判定每个弯曲单元的基高比D是否大于设定的阈值d,若大于,则保留(图 4(c)),否则舍去。
(3) 对所保留下来的每个弯曲单元分别进行障碍距离变换,并取得障碍距离的最大值P为弯曲单元的顶点Pi(图 4(d))。
(4) 用弯曲顶点Pi打断多边形的边界,得到打断的多边形边界线,再建立分段的多边形边界线的Voronoi图(图 4(e)),提取Voronoi图边界线即为该尺度下的多边形的骨架线(图 4(f))。
(5) 改变双缓冲变换L值,重复步骤(1)~(4),可以得到不同尺度下的多层次骨架线。图 5为将双缓冲变换宽度L分别设为10.5 km、10 km、5 km、1.1 km(对应记为L1、L2、L3、L4),所得到的多层次多边形骨架线。

|
| 图 4 某一尺度下的骨架线提取分解图 Fig. 4 Schemes of skeleton extraction with a scale L |

|
| 图 5 某湖泊多边形(1∶400万)的多尺度骨架线的提取 Fig. 5 Multiscale skeletons extracted from a polygon in the 1∶4 000 000 lake map |
观察图 5中的多尺度骨架线可以发现:对同一图形,较大变换尺度对应于图形的主要骨架线,代表着图形的主体形态。随着变换尺度L的减小,所提取的多边形骨架线越来越精细。并且,较小变换尺度下的骨架线包含了所有在此之上的较大变换尺度下的骨架线。也即,骨架线在不同尺度的重合次数可以代表骨架线的主次性。
利用该规律,本文进一步对所得到的多尺度骨架线进行结构化组织,具体步骤如下:
(1) 将不同变换尺度Li下的骨架线分别二值化处理,即将骨架线上的像元赋为1,背景像元赋为0。
(2) 将这些骨架线二值图进行叠加运算,即对应像元的像元值进行和运算,从而利用骨架线在各变换尺度中的重复次数来表示骨架线像元的权值,权值越大,则说明该骨架线处于主要层次。如图 6中的权值为4的像元,表示在4个变换尺度都出现的骨架线像元,它们代表着该图形的主体骨架。而权值为1的像元,表示在4个变换尺度中只出现过一次的骨架线像元,它们代表着图形的最细微骨架。

|
| 图 6 1∶400万湖泊多边形多层次骨架线结构化 Fig. 6 Structured schemes of multi-scale skeletons extracted from a polygon in the 1∶4 000 000 lake map |
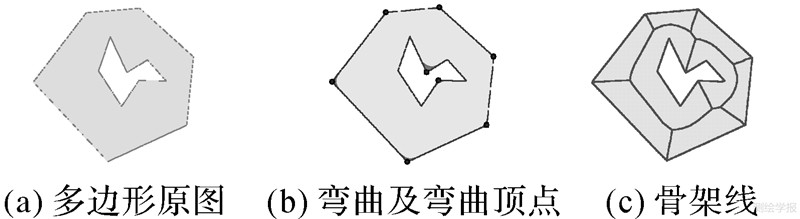
方法的通用性:传统骨架线提取方法并非对所有多边形都适用[16]。与现有方法相比,本文方法除了能够有效提取湖泊等复杂多边形的骨架线之外,而且对于简单多边形和含岛洞等复杂多边形也同样适用(图 5、图 7~图 10)。

|
| 图 7 简单多边形的骨架线提取 Fig. 7 Skeleton extraction of a simple polygon |
|
| 图 8 含岛洞多边形的骨架线提取 Fig. 8 Skeleton extraction of a polygon with a hole |

|
| 图 9 含噪声边缘的多边形提取 Fig. 9 Skeleton extraction of a polygon with noisy error in boundary |

|
| 图 10 无限曲率的多边形提取 Fig. 10 Skeleton extraction of an infinite curvature polygon |
骨架线提取层次的可控性:本文中提取的多边形骨架的层次和密度可以通过双缓冲变换宽度来控制,双缓冲变换尺度L越小,所选取的弯曲单元越多,则得到的骨架线分支越多越精确(图 5和图 10)。
抗噪性:一些方法提取的骨架线易受到边界噪声的干扰,容易出现毛刺[13, 28]。对此,本文方法可以通过控制基高比阈值d来剔除细小的弯曲单元,以此避免提取结果不受图形边界噪声的影响(图 5和图 9)。
拓扑一致性:一些传统方法难以处理曲率无限的情况,对于这种问题,文献[10]根据计算机辅助几何原理设计一序列算法来解决无限曲率附近的中轴点提取问题,从而使得中轴保持拓扑一致。如图 10(c)所示,本文方法对于曲率无限多边形,能够直接提取其骨架线,不用进行进一步处理,且方法简单有效,并可保持骨架线拓扑一致性。
层次组织具有宏观性:目前对骨架线的研究多是针对多边形骨架线的提取,而多边形骨架线本身具有多层次性,目前研究多层次骨架线的文献甚少,代表性的有文献[29]提出的顾及多因素的面状目标多层次骨架线提取,骨架线层次结构化采用的是二叉树的表达形式,结构化原理类似水系的SHREVE分级方法。该方法虽然分出骨架线的层次,但是所有骨架线均被节点打断,不能满足从宏观上识别目标的主骨架线的需要。本文的层次划分与河网层次的划分不同,不是简单地依据节点打断线,在宏观结构上没有破坏骨架线的整体性,因而能从宏观上识别目标的主骨架线,如图 6所示。
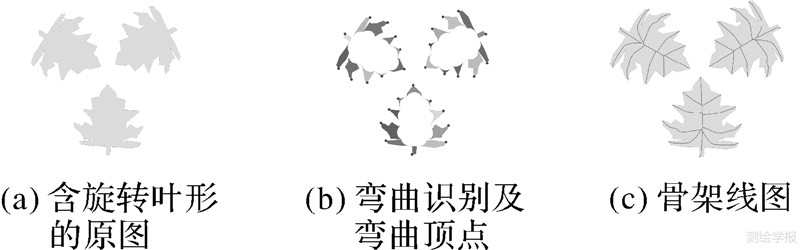
旋转不变性:传统方法中,尤其是利用几何算法、模板来提取骨架线的方法,一旦图形发生旋转或者相对坐标发生变化,则提取的骨架线也会发生变化[13]。如图 11(c)所示,本文方法提取的骨架线不受图形旋转的影响,具有旋转不变性。
|
| 图 11 带旋转的图形的骨架线提取 Fig. 11 Skeleton extraction of rotating leaf shapes |
形态特征保持性:利用双缓冲变换对图形形态的保持能力,本文方法能够在算法中一定程度上考虑面状地理现象的走向和分布因素,使得提取结果能够保持多边形的形态特征,符合视觉感受结果。例如,对于图 5中的1∶400万某湖泊多边形数据,随着双缓冲变换宽度L,本文方法可以得到不同观察尺度下的多边形骨架线。可以看到,变换尺度L1=10.5 km所对应的骨架线反映了该湖泊多边形的主体走向。而图 7(c)的骨架线呈现出一个大致圆心、且各方向骨架线分支的长度大致相等的形态,由此可判断该多边形的形态分布近似为圆形。图 11则说明该方法提取结果反映了原多边形的叶形分布特性。
4 结 论本文利用双缓冲变换和障碍距离变换,提出一种面状地物的多层次骨架线提取方法,主要通过控制双缓冲变换尺度来控制弯曲单元的大小和密度,从而提取不同密度和层次的骨架线。与现有方法相比,本文方法具有良好的通用性,能有效提取含直边、曲边的简单多边形的骨架线,也同样适用于含岛洞的复杂多边形。并且,该方法不受边界噪声的干扰,所提取的骨架线具有良好的连通性、准确性和拓扑一致性,不受图形旋转的影响。本文方法的最显著特点是能够提出多边形的多层次骨架线,可应用于面状要素的多尺度形态特征识别和相似性匹配等方面。后续工作将研究如何将本文方法应用于地图综合中的多边形综合效果评价问题。
| [1] | WU Hehai. Map Generalization Theory and Techniques [M].Beijing: Publishing House of Surveying and Mapping,2004.(毋河海.地图综合理论基础与技术方法研究[M].北京: 测绘出版社,2004.) |
| [2] | DU Shihong,DU Daosheng. A New Raster Based Algorithm for Extracting Main Skeleton Line of Polygon[J]. Journal of Wuhan Technical University of Surveying and Mapping,2000,25(5):432-436.(杜世宏,杜道生. 基于栅格数据提取主骨架线的新算法[J].武汉测绘科技大学学报,2000,25(5): 432-436.) |
| [3] | DU Ruiying,LIU Jingnian. A Research on Automatic Placement of Geo-Name in Area Feature [J]. Acta Geodaetica et Cartographica Sinica,1999,28(4):365-368.(杜瑞颖,刘镜年. 面状地物名称注记的自动配置研究[J].测绘学报,1999,28(4): 365-368.) |
| [4] | FRANZ A. Weighted Skeletons and Fixed Share Decomposition [J]. Computational Geometry,2008,40(2): 93-101. |
| [5] | SHAMIR A, SHAHAN A. Skeleton Based Solid Representation with Topology Preservation[J]. Graphical Models,2006, 68(3): 307-321. |
| [6] | XU Limin,XUE An. Terrain Reconstruction from Contours by Skeleton Extraction Using Delaunay Triangulation and Voronoi Diagram[J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2009,45(4):43-48.(许丽敏,薛安.基于Delaunay三角网与Voronoi图联合提取等高线骨架的地形重建算法研究[J].北京大学学报:自然科学版,2009,45(4):43-48.) |
| [7] | OGNIEWICZ R L, KUBLER O. Hierarchic Voronoi Skeletons [J].Pattern Recognition, 1995, 28(3): 343-359. |
| [8] | MAYYA N, RAJAN V T. Voronoi Diagrams of Polygons: A Framework for Shape Representation [C]//Proceedings of 1994 IEEE Computer Society Conference .[S.l.]:IEEE,1994. |
| [9] | OGNIEWICZ R, ILG M. Voronoi Skeletons: Theory and Applications[C]//Proceedings of 1992 IEEE Computer Society Conference .[S.l.]:IEEE,1992. |
| [10] | CHANG Yonghan, SONG Hwakwon, CHOI Hyeongin. Media Axis Transform of a Planar Domain with Infinite Curvature Boundary Points [J].Computer Aided Geometric Design,2012,52(4):147-153. |
| [11] | HU Peng,WANG Haijun,SHAO Chunli,et al. Polygon Medial Axis Problem and the Algorithm [J]. Geomatics and Information Science of Wuhan University,2005,30(10):853-857.(胡鹏,王海军,邵春丽,等. 论多边形中轴问题和算法[J]. 武汉大学学报:信息科学版, 2005,30(10): 853-857.) |
| [12] | DU Yongqiang, WANG Xiao, LIU Huixia. Character Differentiating between Voronoi Diagram and Medial Axis of Polygon [J]. Computing Technology and Automation,2005,24(3):60-62.(杜永强,王霄,刘会霞. 二维Voronoi图和中轴的特征区分[J]. 计算技术与自动化,2005, 24(3): 60-62.) |
| [13] | ANDRES S M,JOCHEN L. Skeleton Pruning by Contour Approximation and the Integer Media Axis Transform [J]. Computers and Graphics, 2012(4):151-159. |
| [14] | FRANK Y S,CHRISTOPHER C P. A Skeletonization Algorithln by Maximal Tracking on Euclidean Distance Transform[J]. Pattern Recognition,1995,28(3): 331-341. |
| [15] | GE Y. On the Generation of Skeletons from Discrete Euclidean Distance Maps[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1996, 11(18): 1055-1066. |
| [16] | GUO Bangmei,WANG Tao. Research on Algorithm of Polygon Skeleton Line Extracting[J].Bulletin of Surveying and Mapping,2010,17(12): 17-19, 53.(郭邦梅,王涛.面状要素骨架线提取算法的研究[J].测绘通报,2010,17(12): 17-19, 53.) |
| [17] | LI Xiaojun,FANG Jianglong,JIANG Zhifeng. Research of an Algorithm for Extracting Central Skeleton Line of TrueType Fonts[J].Journal of Mechanical Manufacturing,2010,48(1):19-21.(李小军,方江龙,蒋知峰.TrueType字体中心骨架线提取算法研究[J].机械制造,2010,48(1): 19-21.) |
| [18] | CHEN Huirong,ZHENG Yidong,GUAN Haibo. Improvement of Douglas-Peucker Algorithm Based on Skeleton Line[J].Hydrographic Surveying and Charting,2011,31(5): 18-20.(陈惠荣,郑义东,关海波.基于骨架线的Douglas-Peucker算法改进[J].海洋测绘,2011,31(5): 18-20.) |
| [19] | LIU Xiufang,YANG Yongping,LUO Ji. Research on Chart Contour Automatic Cartographic Generalization Based on Arc Info[J].Hydrographic Surveying and Charting,2010,30(5):46-48.(刘秀芳,杨永平,罗吉.基于内侧缓冲区算法的多边形骨架线提取模型[J].海洋测绘,2010,30(5):46-48.) |
| [20] | LIU Jing. Design and ImpleMentation of Skeletonization in GIS Cartography[J].Journal of South-Central University for Nationalities(Nature Science Edition),2007,26(4):78-80.(刘晶.GIS制图中骨架提取算法的设计与实现[J].中南民族大学学报:自然科学版,2007,26(4):78-80.) |
| [21] | DAVID T G C. Terrain Reconstruction from Contours by Skeleton Construction [J]. GeoInformatica,2000,4(4): 349-373. |
| [22] | MASAYUKI H,ALEXANDER G B,TOSIYASU L K. A Skeleton-based Approach for Detection of Perceptually Salient Features on Polygonal Surfaces [J]. Computer Graphics,2002,21(4):689-700. |
| [23] | DOMINIQUE A,JEAN DANIEL B,HERBERT E. Stability and Computation of Medial Axes:A State-of-the-Art Report[C]//Conference on Mathematics and Visualization. Berlin: Springer Verlag, 2008. |
| [24] | ZHU Weisong. A Study of Distance Transform Based Fiber Skeleton Determination Algorithm[D].Nanchang:Donghua University,2008.(朱维松.基于距离变换的纤维骨架提取算法研究[D]. 南昌:东华大学,2008.) |
| [25] | EFTEKHARIAN A A,HOREA T I. Distance Functions and Skeletal Representations of Rigid and Non-rigid Planar Shapes [J]. Computer-Aided Design,2009,41(12): 865-876. |
| [26] | GAO Wei, ZHANG Jianbo. The Algorithm and Its Application of Best Route Analysis Based on Raster Data Mode [J].Journal of Heilongjiang Institute of Technology,2006,18(1):22-24.(高伟,张剑波.基于栅格数据模型的最优路径分析算法及实现[J].黑龙江工程学院学报,2004,18(1):22-24.) |
| [27] | VASILIS M, ANDRONIKI X, BYRON N,VASILIS V. The Use of Epsilon-Convex Area for Attributing Bends along a Cartographic Line[C]//Proceedings of 12th International Cartographic Conference.Coruna:[s.n.],2005. |
| [28] | IVANOV D,KUZMIN E, BURTSEV S. An Efficient Integer-based Skeletonization Algorithm [J]. Computers and Graphics, 2000, 1(24): 41-51. |
| [29] | WANG Tao, WU Heihai. Extraction of Hierarchical Skeleton of Areal Object Based on Multivariate Analysis[J].Geomatics and Information Science of Wuhan University,2004,29(6):533-536.( 王涛,毋河海.顾及多因素的面状目标多层次骨架线提取[J].武汉大学学报:信息科学版,2004,29(6):533-536. |



