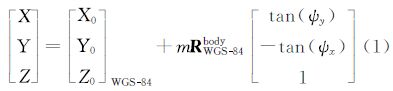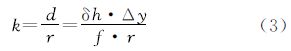2. 国家测绘地理信息局 卫星测绘应用中心，北京 100830
2. Satellite Surveying and Mapping Application Center,National Administration of Surveying,Mapping and Geoinformation,Beijing 100830,China
1 引 言
资源三号卫星是我国第一个高分辨率民用立体测绘卫星，于2012年1月9日成功发射。该卫星兼有测绘和国土资源普查的功能，用于1∶50 000立体测图及更大比例尺基础地理信息产品的生产和更新，以及开展国土资源调查与监测。文献[1, 2]分别对资源三号测绘卫星影像产品进行了精度验证，经验证表明资源三号测绘卫星影像产品能满足1∶50 000测图精度要求。
几何模型是影像数据几何处理的关键，其建立了影像上像点坐标与地面坐标的对应关系。为了便于资源三号影像的应用，资源三号卫星发布的基础产品是传感器校正产品。传感器校正产品是基于理想的线阵列传感器重成像生成的无畸变的影像产品，该产品提供有理多项式模型(rational function model，RFM)参数。有理多项式模型作为通用传感器模型，具有跨平台跨传感器的特点，已广泛应用于高分辨率遥感卫星中[3, 4]。文献[5]研究表明，RFM替代严密成像几何模型精度较低，主要是由于卫星影像中存在畸变和卫星姿态抖动等，ALOS三线阵影像的RFM模型替代严密成像几何模型的精度较低的主要原因是卫星姿态抖动[6]。
严密成像几何模型和高替代精度RFM是卫星影像几何应用的前提，本文首先介绍资源三号测绘卫星及其严密成像几何模型，基于多片CCD影像的严密成像几何模型，构建了无畸变的传感器校正产品的严密成像几何模型，并生产了传感器校正产品影像和RFM。理论分析表明，传感器校正产品的生产方式所引入的误差可以忽略不计，并利用安平和嵩山的三线阵数据对资源三号测绘卫星的几何精度进行验证。
2 资源三号测绘卫星严密成像几何模型资源三号测绘卫星采用线推扫式成像，即卫星在行方向(或垂轨向)为中心投影，而在沿轨向通过卫星飞行获取二维影像(若卫星为匀速直线运动即为平行投影)。在精确得知资源三号测绘卫星成像时的内外方位元素基础上，即可建立其严密成像几何模型。
外方位元素包含线元素和角元素两部分。资源三号测绘卫星影像的外方位线元素通过星上双频GPS接收机量测，其测量频率是1 Hz。由于陀螺量测的角元素的相对精度较高，而星敏量测的绝对精度较高，资源三号测绘卫星影像的外方位角元素采用星敏和陀螺联合滤波方式获得，其测量值频率4 Hz。
资源三号测绘卫星在发射前，载荷研制部门测量了卫星的三线阵相机和多光谱相机的内方位元素以及姿态轨道测量设备和相机之间的安装关系，但卫星发射中冲力影响以及太空中热环境等变化，地面测量的内方位元素和有效载荷之间的安装关系不再有效，需进行在轨几何检校[7, 8, 9]。内方位元素包括主点、主距、镜头畸变、CCD在焦平面的分布以及CCD探元的大小等。从物理意义上来说，CCD探元大小不规则等CCD相关的误差和镜头畸变是不同的，但两者对成像和定位影响不可区分，如CCD探元大小误差和主距误差都影响影像的分辨率。因此，资源三号测绘卫星相机的内方位元素用本体坐标系下CCD探元的指向角(ψx,ψy)表示，其中(x,y)为影像坐标系xoy下坐标，其定义如图 1所示。
|
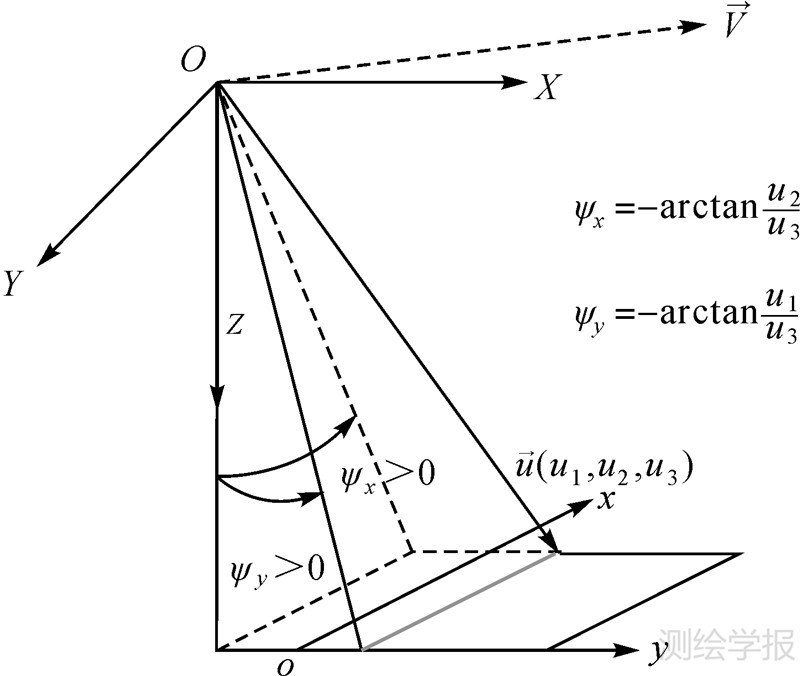
| 图 1 成像光线在本体坐标系下指向角与内方位元素关系 Fig. 1 The relation between look angle and interior orientation elements under body coordinate system |
图 1表示CCD探元光线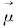
在本体坐标系OXYZ下指向(μ1,μ2,μ3)与内方位元素(ψx,ψy)关系。其中OXYZ为卫星本体坐标系，其中
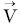为卫星飞行方向，X轴为沿轨向，Z轴指向地心，Y轴与其他两轴构成右手直角坐标系。而影像坐标系xoy以影像左上角点为原点，y轴指向沿轨向，x轴指向扫描方向。因此，通过像元的影像坐标系下坐标(x,y)内插标定后探元指向角(ψx,ψy)，即可得到像点在本体坐标系下指向角[tan (ψy)－tan (ψx)1]T。依据内外方位元素和像点、物点、投影中心3点共线原理建立起严密成像几何模型
资源三号测绘卫星为了获取较大的幅宽，其三线阵全色相机和多光谱相机均采用多片时间延迟积分(time delay and integration,TDI) CCD拼接的方式。星上下传原始影像数据是分片CCD的影像，让用户为每片影像建立对应的成像几何模型将增加用户使用的难度。为了方便用户使用，需要将全色相机的分片CCD影像拼接为单景影像，而多光谱相机要完成各个波段内CCD影像拼接和波段间的配准；并提供高精度的成像几何模型参数。
基于虚拟CCD重成像的拼接方式可以生成视觉无缝且几何无缝的传感器校正产品影像，而且由于消除了影像中的各类畸变，使得传感器校正产品的RFM替代精度较高。这种方法生产的无畸变传感器校正产品影像满足线中心投影，且生产过程中引入的投影差误差和交会误差可以忽略不计。
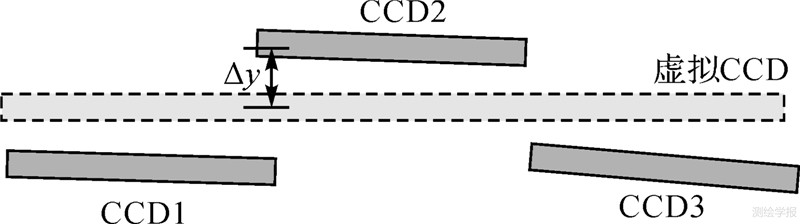
3.1 TDI CCD影像畸变分析与消除类似线推扫式传感器影像内外方位元素的区分方法，将影像上的畸变分为两类：内畸变和外畸变[7, 13]。其中，内畸变主要是指相机内部的畸变引起的CCD影像变形，主要包括以下3个部分：① 光学镜头畸变，主要包括径向畸变、偏心畸变[14]；② CCD畸变，主要包括CCD的大小不一致引起影像上各个像元对应地面范围变化，CCD之间不平行以及不共线(如图 2所示)将引起相邻CCD端点处像元获取地物不同，严重时可能使得成像中“有缝”(即影像不能完全覆盖地面)，CCD不平行于焦面上，使得各个CCD像元大小不一；③ 主点和主距的误差，将影响投影中心的位置。
|
| 图 2 虚拟CCD与真实CCD分布示意图 Fig. 2 The sketch map of virtual CCD and real CCDs distribution |
外畸变主要由以下3个原因所造成：① CCD积分时间不一致，由于资源三号卫星三线阵相机和多光谱相机均采用TDI CCD进行成像，其积分时间受纬度和地面高低起伏等因素影响，造成积分时间存在跳变，这将引起像元在沿轨向地面覆盖范围不一致；② 轨道参数中存在高频噪声，轨道参数中存在高频噪声将直接影响定位精度；③ 卫星飞行过程中姿态抖动导致影像的RFM替代精度不高[6]。
基于虚拟CCD重成像可以消除影像内畸变。重成像时应用的虚拟CCD相机具有以下特点：不考虑镜头畸变，为理想小孔成像；虚拟CCD是位于焦平面上的单组CCD；像元大小相同，等间隔分布；虚拟CCD覆盖各片CCD的成像范围。利用在轨几何检校的内方位元素(ψx,ψy)，计算出其位于焦平面上的像点坐标，拟合出最优的虚拟CCD位置，使得生产过程中引入的误差最小，如图 2所示。由于几何检校时，补偿了主点和主距误差，因此虚拟CCD影像中消除了主点和主距误差。
基于虚拟CCD重成像同时可以消除外畸变。通过积分时间规划(即一景之内每行影像的积分时间相同)，消除积分时间跳变对轨道和姿态内插的引起的成像几何模型的平滑性影响；针对轨道参数的高频噪声可通过滤波或直接利用精密轨道数据，消除轨道参数引起的外畸变；卫星姿态数据中的抖动可通过姿态低通滤波消除。
3.2 虚拟CCD重成像引入误差分析由于原始TDI CCD交错排列，故虚拟CCD与原始CCD之间在沿轨向存在错开现象，如图 2中Δy所示。当利用虚拟CCD的探元替代TDI CCD的探元时，其相对于投影中心在沿轨向成一定夹角，该夹角会引起投影差的差异。由于相机的主距f是相对稳定的，沿轨向夹角可转化为焦平面上CCD沿着轨道方向的距离Δy。重成像过程中高程不准确，会引入投影差误差，其误差的大小受虚拟CCD和TDI CCD对应探元相对于投影中心夹角和高程误差的影响。高程误差的引入主要包含两个因素：① DEM精度有限；② 卫星影像定位误差。当立体像对中同时存在投影差，前方交会求解地面点高程时引入交会误差。
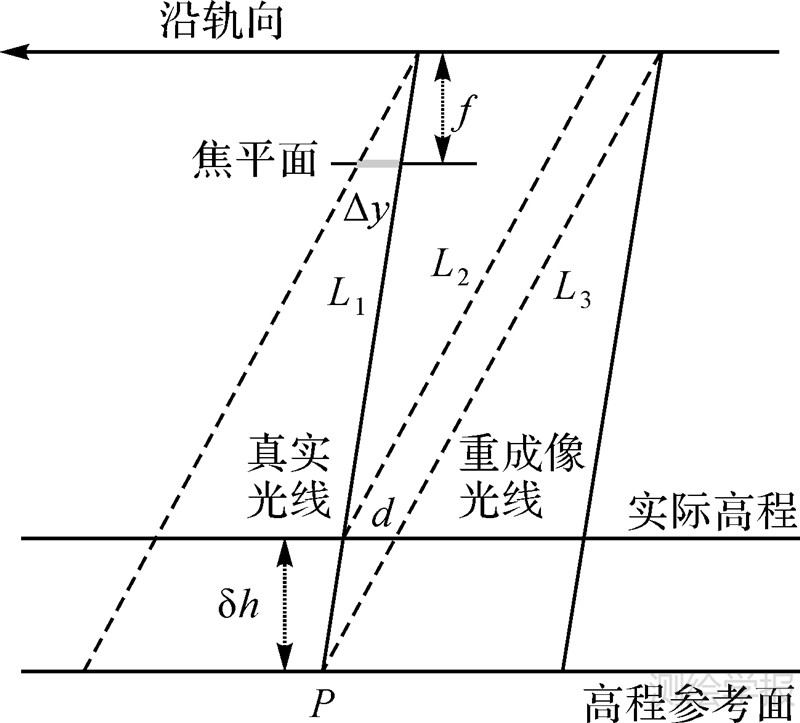
3.2.1 投影差误差图 3为卫星飞行沿轨向剖面图，其中实线和虚线分别表示真实成像光线和重成像光线，地面点P实际成像光线为L1，重成像时成像光线方向变化，改变量由虚拟CCD与TDI CCD在焦面上沿轨向错开Δy和相机主距f决定。当P点高程已知时，重成像光线为L2，此时不会引入投影差误差。然而P点高程存在误差δh，造成重成像光线平移为L3，其物方偏移值为d。焦平面与实际高程面平行，由相似三角形可以得到物方偏移值d、光线在焦面上的错开Δy、相机主距f以及高程误差δh之间的关系如下
将式(2)中的物方距离d除影像分辨率r即可得到其对应像方投影差误差k
|
| 图 3 高程不准造成的像点偏移示意图 Fig. 3 The sketch of image point’s offset caused by the error of elevation |
资源三号三线阵全色相机的CCD间Δy均小于0.5像素，根据式(3)只有当高程误差为106 m时，才会引起一个像元的投影差误差。而全球最高峰珠穆朗玛峰高程为8844 m，故资源三号测绘卫星三线阵全色影像在虚拟重成像时候可忽略投影差误差。因此，全色相机传感器校正产品生产中，高程参考面采用该景范围内的平均高程面。
资源三号上搭载了全反式拼接的多光谱相机，获取的多光谱影像有4个波段，每个波段对应有3片TDI CCD。针对资源三号多光谱相机，采用虚拟理想CCD同时对多光谱4个波段重成像的方式完成波段内拼接和波段间配准工作。多光谱相机各个波段TDI CCD在焦面上沿卫星飞行方向排布，第1波段与第4波段之间距离最大，因此第1波段与第4波段的探元指向出现相对较大的夹角，而波段内CCD在沿轨向的夹角相比于波段间的夹角可以忽略不计。根据公式(3)，当地面实际高程与高程参考面的误差在3.96 km时，将会造成第1波段与第4波段在沿轨向偏移差1像素。若要保证重成像影像波段间错位不超过0.2像素，虚拟重成像中采用高程参考面误差在0.79 km以内。因此，针对多光谱相机来说为满足波段内CCD拼接和多波段间配准精度，在虚拟重成像中采用SRTM(the shuttle radar topography mission) DEM[15]作为高程参考面，减少因生产流程而引入的误差。
3.2.2 交会误差资源三号测绘卫星采用前下后视相机构建立体模型，此时具有最大的基高比。在对前后视相机进行拼接的过程中，成像光线的改变将使得高程交会点位置发生变化，即重成像会引入交会误差。相比于投影差误差分析时，交会误差还受姿态抖动的影响。
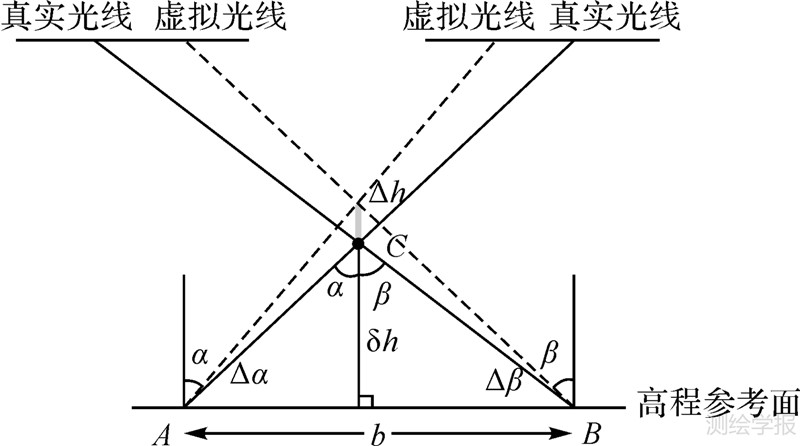
如图 4所示，资源三号前后视同时对地面点C成像时，由于重成像时投影到高程参考面上，成像点分别为A和B，其中A和B之间距离为b。虚拟光线与真实光线方向变化Δα、Δβ和高程参考面高程误差δh引起虚拟光线交会点与地面点C之间存在交会误差Δh。前后视相机成像时光线夹角α、β决定了基高比，由三角形相似原理可知，基高比等于b/δh。由三角公式并求对α、β偏导可以得到
因此，虚拟重成像引起的高程误差主要有高程参考面误差δh，相机倾角α、β和角度变化值Δα、Δβ。其中，角度变化包含两个部分：① 由于虚拟CCD替代原始CCD时，造成相对较为固定的角度改变;② 由于姿态滤波时，造成成像光线方向变化，对于资源三号测绘卫星而言主要是俯仰角的影响。资源三号卫星，其前后视相机的α、β角均约为22°，同时考虑俯仰角滤波和重成像的影响，当高程参考面高程误差为1000 m，重成像引起的高程误差为1.18 cm，对于资源三号前后视沿轨向3.7 m的分辨率来说，此误差可忽略。
|
| 图 4 虚拟成像引入高程误差 Fig. 4 The elevation error caused by virtual imaging |
通过内外畸变的消除，建立无畸变的传感器校正产品严密成像几何模型，依据该模型和多片CCD影像的严密成像几何模型以及高程参考面，建立了传感器校正产品与多片CCD的一一对应关系，基于这种对应关系即可完成灰度重采样，生产传感器校正产品影像。
当前RFM已经作为一种通用传感器模型广泛应用于摄影测量处理系统中，资源三号卫星提供RFM作为传感器校正产品几何模型。有理多项式系数计算有两种方法：地形相关和地形无关。其中，地形无关的求解方案是基于严密成像几何模型建立虚拟控制格网和检查格网，利用控制格网点求解有理多项式系数，利用检查格网评价模型的精度[16]。
4 试验分析 4.1 试验数据简介采用河北安平地区和河南登封地区的数据进行资源三号传感器校正产品的精度进行分析和评估。其中河北安平为华北平原地区，高程起伏较小。而河南登封地区为山地，高程起伏1255 m。安平数据获取时间为2012年2月18日，登封地区数据获取时间为2012年3月1日。
其中登封地区的地面控制数据为检校场数据，该地区尽管有大量控制点，但这些控制点原本是针对0.2 m的航空数据布设的，因此对于3.7 m分辨率的资源三号前后视全色数据来说，大量控制点无法识别，可识别的控制点仅有36个，这些控制点在影像范围内均匀分布。安平地区量测了574个地面控制点。安平地区为农田区域，缺少大量稳定地物作为控制点，所以选择道路交叉口。但外业测量员将其中很大一部分控制点布设到农田的角点处，这些控制点尽管在地面上容易辨识，但在全色影像上却无法准确刺点。因为角点处的模糊现象会使得角点的位置不准确。在删除识别不准确的控制点后，剩余474个控制点，控制点分布如图 5所示。
|
| 图 5 影像及控制点分布图 Fig. 5 Images with GCP information |
由于无畸变传感器校正产品为消除影像各种畸变后的理想线中心投影影像，因此其RFM替代精度较高。当消除内部畸变后，RFM替代精度优于0.7像素。在完成姿态滤波等外畸变消除后，RFM替代精度优于0.01像素。
本文采用平差对资源三号测绘卫星三线阵传感器校正产品进行几何精度分析和验证。对线阵列传感器卫星进行平差方法有3种：① 基于像方的多项式模型；② 基于物方的多项式模型；③ 对卫星的轨道和姿态进行修正[17, 18, 19]。其中采用像方仿射变换模型是最常用，且精度很高[20]。基于仿射变换模型，至少需要3个控制点求解6个未知参数。为了获得较好的精度，采用四角点布控方案[21]。
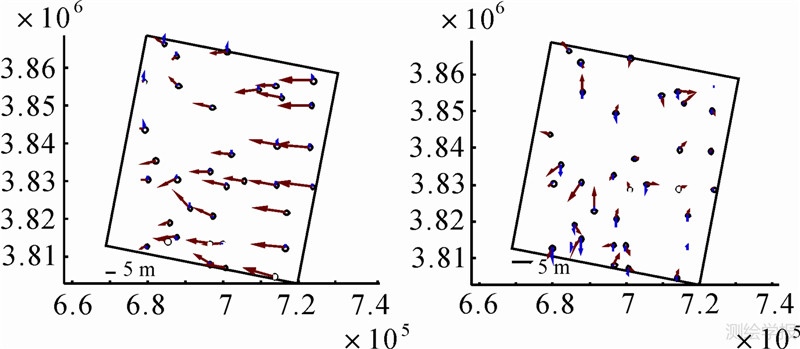
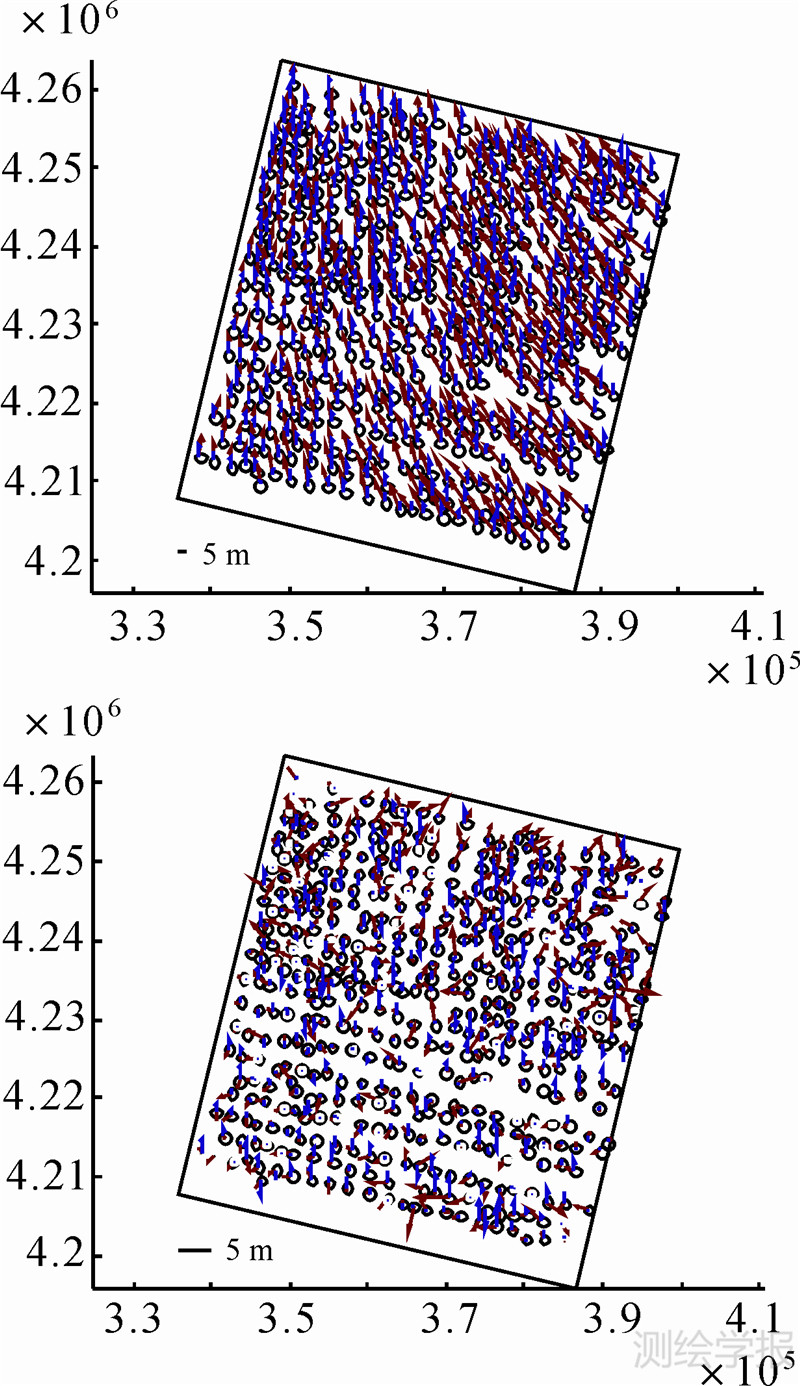
登封地区资源三号三线阵数据无控制点时，即将所有控制点当检查点进行平差，其检查点中误差为10.10 m，高程为1.88 m。四角点布控，其余点作检查点，检查点中误差平面为2.60 m，高程为1.58 m。其误差分布如图 6所示，图中红色为平面误差，箭头指向误差方向；蓝色为高程误差，箭头向上表示正值，向下表示负值。安平地区有大量控制点，为了减弱控制点选择误差的影响，采用四角的双点布控方案。无控平差时，其平面精度为15.11 m，高程精度为8.30 m；四角点布控时，其平面中误差为1.78 m，高程为1.46 m。其误差分布如图 7所示。从图 6和图 7中可以看出，当进行无控平差时，影像的误差呈现明显的系统性，当进行四角点布设控制点平差后，影像定位精度大幅度提高，且误差呈现随机性的特点。
|
| 图 6 登封地区无控制点平差(左)和四角点控制平差(右)误差分布图 Fig. 6 The error distributions of Dengfeng area without (left)/ with four corner(right) GCPs |
|
| 图 7 安平地区无控制点平差(上)和四角点控制平差(下)误差分布图 Fig. 7 The error distributions of Anping area without (top)/ with four corner(lower) GCPs |
针对两线阵平差试验，对于安平地区，两线阵平差检查点中误差在平面上为2.44 m，高程上为1.60 m。登封地区两线阵平差检查点中误差平面上为2.88 m，高程上为1.66 m，其误差分布如图 8所示。相比于前后视构成的两线阵立体，三线阵立体平面上增加了多余观测，而且其下视分辨率要高于前后视分辨率，能显著提高平面精度。
|
| 图 8 两线阵平差误差分布图 Fig. 8 The error distributions of two-line adjustment |
资源三号卫星影像应用的关键之一在于其高精度成像几何模型的建立。为了方便用户使用，资源三号主要发布无畸变的传感器校正产品，该产品带有RFM。该产品消除了内外畸变，且生产过程中引入误差可以忽略，故进行平差时精度很高。
利用虚拟CCD重成像的方式，消除了镜头、CCD以及主点主距的内畸变和积分跳变、轨道高频噪声以及姿态抖动引起的外畸变。基于多片CCD的严密成像几何模型和传感器校正产品的严密成像几何模型，在一定的高程参考面下即可建立两者的对应关系，完成影像灰度的重采样，利用地形无关求解方式计算的有理多项式系数的替代精度优于1%像素。
在重成像过程中，由光线改变和高程参考面不准确而引入的投影差误差对于资源三号全色相机来说可以忽略不计，对于前后视影像构建的立体模型来说，1000 m的高程参考误差引入的交会误差为1.18 cm，可忽略不计。为同时解决多光谱影像的波段内的拼接与波段间的配准问题，采用了单个理想CCD重成像的方式，生产了多光谱影像。由于其波段间沿轨向错开较大，需要利用全球SRTM DEM数据作为高程参考面。
资源三号卫星三线阵平差和两线阵平差相比，在平面上增加了多余观测，提高了平面定位精度，高程精度基本一致。资源三号卫星无地面控制点立体定位精度可以达到15 m。带控制点平差平面误差在3 m之内，高程误差在2 m之内，完全满足1∶50 000测图的需求。
| [1] | TANG Xinming, ZHANG Guo, ZHU Xiaoyang, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation [J].Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198. ( 唐新明,张过,祝小勇,等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报,2012, 41(2): 191-198.) |
| [2] | LI Deven. China′s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3 [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317-322. ( 李德仁. 我国第一颗民用三线阵立体测图卫星-资源三号卫星[J]. 测绘学报,2012, 41(3):317-322.) |
| [3] | DIAL G, BOWEN H, GERLACH F, et al. IKONOS Satellite, Imagery and Products [J]. Remote Sensing of Environment, 2003, 88(1-2): 23-36. |
| [4] | SAUNIER S, GORYL P, CHANDER G, et al. Radiometric, Geometric, and Image Quality Assessment of ALOS AVNIR-2 and PRISM Sensors [J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3855-3866. |
| [5] | TOUTIN T. Review Article: Geometric Processing of Remote Sensing Images: Models, Algorithms and Methods [J]. International Journal of Remote Sensing, 2004, 25(10): 1893-1924. |
| [6] | SCHWIND P, SCHNEIDER M, PALUBINSKAS G, et al. Processors for ALOS Optical Data: Deconvolution, DEM Generation, Orthorectification, and Atmospheric Correction [J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 4074-4082. |
| [7] | POLI D, TOUTIN T. Review of Developments in Geometric Modelling for High Resolution Satellite Pushbroom Sensors [J]. The Photogrammetric Record, 2012, 27(137): 58-73. |
| [8] | JACOBSEN K. Calibration of Optical Satellite Sensors [M].Casteldefels: International Calibration and Orientation Workshop EuroCOW,2006. |
| [9] | LEPRINCE S, MUSE P, AVOUAC J P. In-Flight CCD Distortion Calibration for Pushbroom Satellites Based on Subpixel Correlation [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(9): 2675-2683. |
| [10] | JEONG I S, BETHEL J. A Study of Trajectory Models for Satellite Image Triangulation [J]. Photogrammetric Engineering and Remote Sensing, 2010, 76(3): 265-276. |
| [11] | KIM T, DOWMAN I. Comparison of Two Physical Sensor Models for Satellite Images: Position-Rotation Model and Orbit-Attitude Model [J]. The Photogrammetric Record, 2006, 21(114): 110-123. |
| [12] | MCCARTHY D D, PETIT G. IERS Conventions (2003) [M]. Frankfurt: IERS Central Bureau, 2004: 127. |
| [13] | TOUTIN T. State-of-the-art of Geometric Correction of Remote Sensing Data: a Data Fusion Perspective [J]. International Journal of Image and Data Fusion, 2011, 2(1): 3 - 35. |
| [14] | LI Deren, ZHENG Zhaobao. Analytical photogrammetry [M]. Beijing: Publishing House of Survey and Mapping, 1992. (李德仁,郑肇葆.解析摄影测量学[M].北京:测绘出版社,1992.) |
| [15] | FARR T G, ROSEN P A, CARO E, et al. The Shuttle Radar Topography Mission [J]. Rev Geophys, 2007, 45(2): 247-262. |
| [16] | ZHANG Guo. Rectification for High Resolution Remote Sensing Image under Lack of Ground Control Points [D]. Wuhan: Wuhan University, 2005. (张过. 缺少控制点的高分辨率卫星遥感影像几何纠正[D]. 武汉:武汉大学, 2005.) |
| [17] | GRODECKI J, DIAL G. Block Adjustment of High-Resolution Satellite Images Described by Rational Polynomials [J]. Photogrammetric Engineering and Remote Sensing, 2003, 69:59-68. |
| [18] | FRASER C S, HANLEY H B. Bias Compensation in Rational Functions for Ikonos Satellite Imagery [J]. Photogrammetric Engineering and Remote Sensing, 2003, 69(1): 5. |
| [19] | XIONG Z, ZHANG Y. A Generic Method for RPC Refinement Using Ground Control Information [J]. Photogrammetric Engineering & Remote Sensing, 2009, 75(9): 1083-1092. |
| [20] | ORUN A, NATARAJAN K. A Modified Bundle Adjustment Software for SPOT Imagery and Photography: Tradeoff [J]. Photogrammetric Engineering and Remote Sensing, 1994, 60(12): 1431-1437. |
| [21] | ZHANG G, LI Z, PAN H B, et al. Orientation of Spaceborne SAR Stereo Pairs Employing the RPC Adjustment Model [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(7): 2782-2792. |