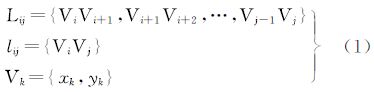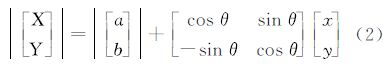2. 南京工业大学 测绘学院,江苏 南京210009
2. College of Geomatics Engineering, Nanjing University of Technology, Nanjing 210009,China
1 当前弯曲识别方法分析
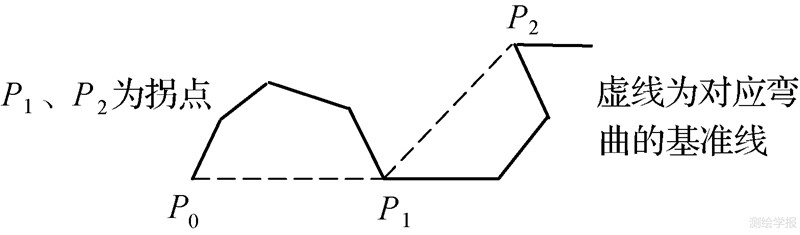
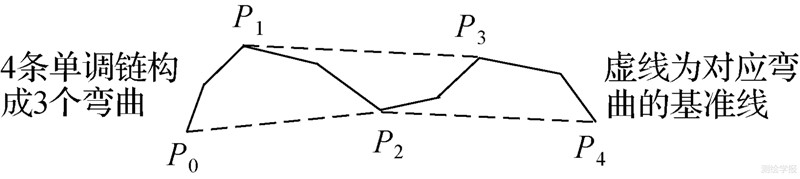
弯曲是曲线的结构特征之一,地图综合中常舍去小于规定尺寸的弯曲、夸大特征弯曲,以保持制图对象的形状特征[1],基于曲线弯曲的地图综合已成为研究的热点。弯曲的识别方法目前主要有3种:拐点法、单调链法、约束Delaunay三角网法。拐点法将若干个沿顺时针或逆时针方向首尾相连的线段集合定义为弯曲[2, 3, 4],其中线段绕动方向变化的点称为拐点,如图 1所示,点P1、P2为拐点,分别为图 1中两弯曲的分界点。单调链法将曲线拆分为沿X、Y方向同时单调的单调链集合,两相邻单调链组成一个弯曲[5, 6],如图 2所示,单调链P0P1、P2P3在X、Y方向同为单调增,单调链P1P2、P3P4在X方向单调增且在Y方向单调减,4条单调链构成3个弯曲。
|
| 图 1 基于拐点的弯曲识别 Fig. 1 Bend identification based on inflection points |
|
| 图 2 基于单调链的弯曲识别 Fig. 2 Bend identification based on monotone chains |
弯曲间存在层次关系,如:一个较大尺寸的弯曲分解为若干个形态各异的较小尺寸的弯曲,通常将满足以上关系的前者称为复合弯曲,称后者为该复合弯曲的子弯曲。以上两种弯曲识别方法的优点是方法简单且容易实现,但都存在着两个主要缺陷:一是它难以识别复合弯曲,两者都不能有效表达弯曲的层次性;二是弯曲识别结果敏感于个别线段的走向,识别时会产生不必要的弯曲。如图 3所示,两方法在A位置都会认为弯曲中断,在B附近又都会产生多个不必要的尺寸较小的弯曲,两者都不能识别曲线左边的复合弯曲,拐点法在判断曲线右边迂回曲线段C部分弯曲时会出错,文献[7]提出引入多种分界点来区分迂回弯曲,但如何选择分界点仍存在不确定性。文献[8]采用单调弧段来划分弯曲,根据弧段类型及大小进行区别化化简,该方法能保持化简后弯曲的轮廓特征,但仍不能表达复合弯曲。

|
| 图 3 拐点法与单调链法的缺陷 Fig. 3 Defects of methods based on inflection points and monotone chains |
基于约束Delaunay三角网的弯曲识别与综合方法先后由文献[9, 10, 11]提出,文献[9]提出联合外部点与曲线点构建Delaunay三角网,然后将曲线作为约束边插入得到约束Delaunay三角网,通过三角形搜索与分类来建立弯曲的二叉树模型。文献[12]在文献[9]的基础上,针对二叉树模型的不足,提出了基于约束Delaunay三角网的弯曲多叉树表达方法。基于约束Delaunay三角网的弯曲识别方法优点是弯曲删除不产生自相交,能一定程度上表达弯曲的层次性,但该方法也存在着一定缺陷,如:对弯曲识别能力仍有限,难以识别平缓曲线上的弯曲;弯曲删除后需局部动态重构,时间成本较高等。
2 曲线弯曲的多叉树表达方法 2.1 利用曲线轴线来划分弯曲曲线形态特征可用曲线上若干个节点来表示,本文中的曲线具体指无自相交的一系列首、尾相连的线段集合。曲线节点k用Vk表示,用Lij表示起点为i、终点为j的曲线,定义曲线Lij的轴线为连接i、j两点的直线段,记为lij,Lij与lij的方向都是从起点i指向终点j。Lij、lij、Vk可以被描述为
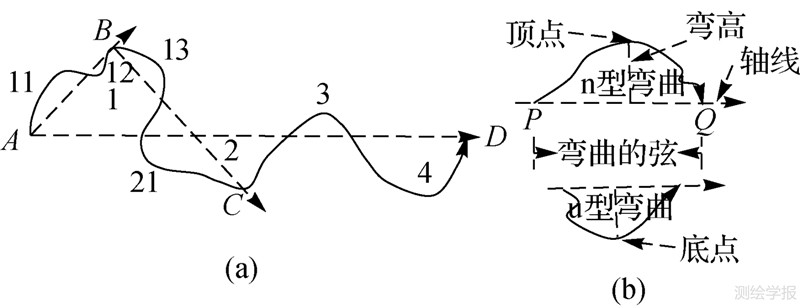
曲线形态特征(如弯曲、平滑、尖锐等)通常是相对于曲线轴线的。Lij表现为左右缠绕着lij,且Lij与lij(或lij的延长线)存在若干交点,这些交点把曲线Lij分为多个曲线段。若沿曲线Lij前进方向对所有交点按序排列,本文把每相邻两交点间的曲线段定义为一个弯曲。同时定义两种弯曲类型:n型弯曲与u型弯曲。从曲线轴线方向看,n型弯曲是两交点间曲线段位于轴线左边的弯曲,u型弯曲位于右边。n型弯曲、u型弯曲上距离轴线的最远点分别称为顶点、底点,顶点或底点到轴线的距离称为弯高,连接弯曲两端点的直线段称为弯曲的弦,弯曲具有弯高、弦长、面积、周长等属性,弯曲的基本特性是其弦与对应曲线段不相交。
如图 4所示,曲线LAD与其轴线lAD有5个交点,将曲线LAD分为4个曲线段,分别形成弯曲1、2、3、4。这4个弯曲不仅彼此相连且对称分布于轴线两侧。根据曲线LAB、LBC与其对应轴线lAB、lBC的关系,可对复合弯曲1、2进行分解,得到11、12、13、21四个子弯曲。由于轴线可在曲线的不同节点间生成,通过构建不同的轴线,可对曲线上不同方向、不同区间上的弯曲进行识别。另外,以曲线轴线为基准划分的弯曲具有连续性、对称性和层次性,符合视觉感受习惯。
|
| 图 4 弯曲定义及其类型 Fig. 4 Definition and types of curve bend |
弯曲的层次化提取是指先提取复合弯曲,然后提取组成复合弯曲的子弯曲,逐层进行。弯曲筛选是指在提取轴线上多个弯曲时,根据弯曲参数(如弯高、弯曲面积等)值进行筛选,只提取参数值相对较大的弯曲,以保证弯曲的典型性。如图 4所示,轴线lAD上的3号弯曲明显小于其他3个弯曲,在提取时应将其剔除。本文采用弯高值为筛选指标,令α(0≤α≤1)为显著性因子,当前轴线上的最大弯高为Hmax,则当前轴线阈值H=αHmax,α值由用户设定,其值越大,则筛选条件越严格,所提取的弯曲越典型。
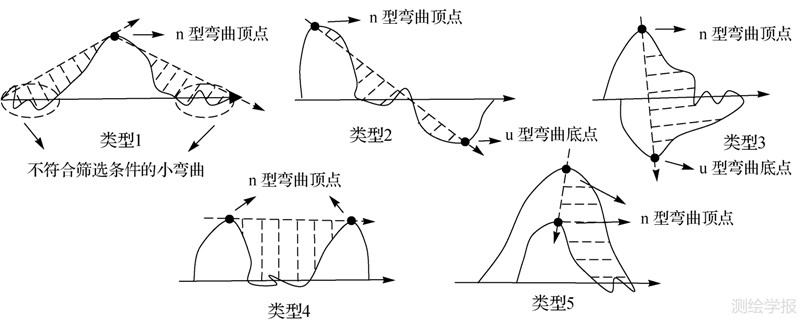
弯曲分裂是指将筛选后的复合弯曲分解为若干个子弯曲。将弯曲投影到轴线上,称其在轴线上对应的范围为弯曲的区间,根据弯曲区间是否重叠可将n、u型弯曲在轴线上的组合分为5类:第1类是n或u型,即只有一个n(或u)型弯曲;第2类是无重叠nu(或un)型,由一个n型弯曲和一个u型弯曲构成,同时两弯曲的区间相邻或相离,无重叠;第3类为重叠nu(或un)型,由一个n型弯曲和一个u型弯曲构成,但两弯曲区间有重叠;第4类、第5类分别为无重叠nn(或uu)型和重叠nn(或uu)型,两类都是由两个同类型弯曲(n或u型)构成,区别在于两弯曲区间前者无重叠而后者有重叠。任何轴线上的弯曲集合都可分解为这5种类型组合。本文约定:根据弯曲的顶点或底点来生成新轴线,在新轴线上递归搜索弯曲。图 5列出了这5种弯曲组合类型及其轴线的生成方法,图中带箭头实线为当前轴线,带箭头虚线为当前弯曲组合分裂后的新轴线,细虚线填充的区域为新轴线的作用范围,图中与轴线反复相交的微小曲线段(如类型1椭圆区域内的曲线段)表示不符合筛选条件的弯曲(即弯高小于阈值αHmax的弯曲)。这些不符合当前轴线筛选条件的弯曲只是暂时被剔除,它们将作为分裂后新轴线上的子弯曲(或子弯曲的组成部分)被提取。可以看出,以弯曲顶点、底点作为新轴线的方式能最大限度分解曲线形态特征。
|
| 图 5 弯曲组合的分裂方式 Fig. 5 Splitting mode of bend combinations |
弯曲分裂的最后是一组最小弯曲(指其轴线左边或右边仅有一个节点的弯曲)。删除与分裂是对弯曲的两个基本操作,弯曲删除表现为用轴线代替弯曲,弯曲分裂是根据弯曲顶点、底点的新轴线进行,因此,本文对弯曲参数的计算也是以曲线轴线为基准。
弯曲的层次化提取方法为:沿着当前轴线方向从左往右识别并筛选弯曲;在所提取弯曲的相邻顶点、底点间生成新轴线;在新轴线上递归提取弯曲。
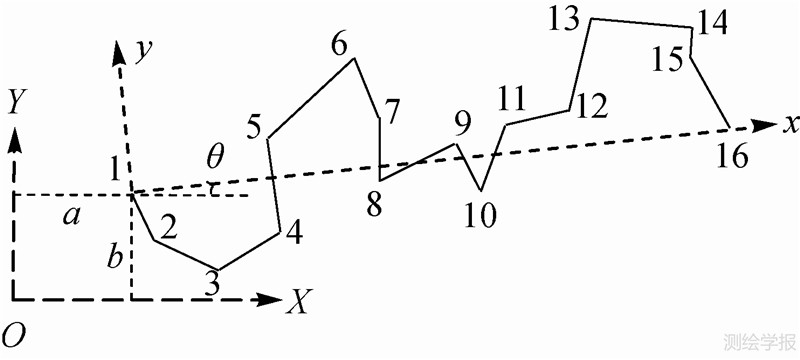
由弯曲定义知,弯曲是曲线上被其与轴线(或轴线延长线)交点分割的曲线段,本文利用坐标系变换来识别弯曲。设图 6中曲线L1、16原坐标系为XOY,在探测轴线l1、16上弯曲时,以轴线l1、16作为新坐标系x轴,轴线起点1为原点,建立新坐标系x1y,两坐标系X轴的夹角为θ,原点偏移量为(a,b),在两坐标系无长度变形情况下,存在转换关系式
|
| 图 6 利用坐标系变换识别弯曲 Fig. 6 Identifying bends using coordinate system transformation |
点1、16在XOY系统下坐标值是已知的,且在新坐标系x1y下坐标分别为(0,0)、(0,length(1、16)),length(1、16)为轴线段l1、16长度,可据此计算公式(2)中的转换参数,然后再按公式(2)来计算曲线L1、16上各点的新坐标值。通过遍历、跟踪各点在新坐标系下y值的正负号变化可识别出曲线L1、16与轴线l1、16是否相交,进而识别所有弯曲及其类型。层次化提取曲线Lij上弯曲的算法如下:
(1) 若i、j两点间无其他节点,则退出搜索;否则,以曲线Lij的轴线lij为新坐标系x轴,进行坐标系变换,求出曲线各点在新坐标系的坐标值。
(2) 遍历曲线Lij的各点新坐标值,根据节点y坐标值的正负号变化确定与轴线的交点,找出轴线lij上的所有弯曲,计算弯曲的弯高、弯曲面积等参数。
(3) 若上一步得到的弯曲都是最小弯曲,则提取,并退出搜索;否则,根据显著性因子α值,筛选上一步得到的弯曲。
(4) 在筛选后弯曲的顶点、底点间生成新轴线。
(5) 对上一步得到的每一条新轴线从左往右逐条重复以上步骤。
2.3 构建弯曲多叉树弯曲的层次化提取方法保证了先提取复合弯曲,而后提取组成复合弯曲的子弯曲。在弯曲分裂过程中,上层复合弯曲或独立分裂为若干个子弯曲,或与同层相邻弯曲一同分裂为若干个子弯曲,弯曲之间的嵌套、相邻等空间关系可用多叉树结构来描述,该多叉树特点有:
(1) 每个树节点与一条轴线相对应,存贮该轴线上经过筛选的一组弯曲,弯曲数组元素间的位置关系与它们在该轴线上对应弯曲间的位置关系相一致。
(2) 树的根节点与曲线的初始轴线相对应,其存贮的弯曲数组为沿着曲线首、尾端点连线所提取的弯曲集合。
(3) 树的子节点与其父节点弯曲分裂后的一条新轴线相对应,存贮该轴线上的弯曲集合。
(4) 树中同层兄弟节点间的左右邻接关系与它们父节点分裂后新轴线间的左右邻接关系一致。
(5) 树的每个非叶节点拥有子节点数目最多为它本身所存贮的弯曲数目加一。
(6) 叶节点存贮的弯曲为一组最小弯曲。
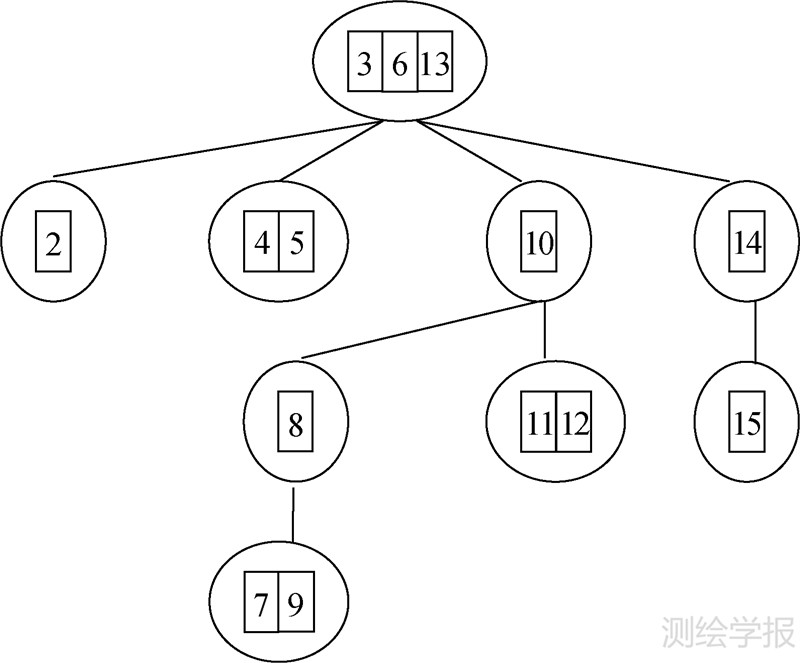
图 7是图 6曲线对应的弯曲多叉树,取α=0.3,为简单起见,用弯曲顶点或底点来表示具体弯曲。该多叉树即为弯曲的层次化提取结果,树的父、子节点所存贮的弯曲分别表示位于上下层关系的复合弯曲与其子弯曲,树中同层兄弟节点所存贮的弯曲位于同一层次。
|
| 图 7 弯曲多叉树 Fig. 7 Multi-way tree of bends |
弯曲的面积、弯高、周长等参数都从不同侧面描述了曲线结构特征,利用弯曲参数或其组合进行综合为用户提供了很大的灵活性。在图形简化过程中,空间目标之间的拓扑关系也会发生变化[13],主要表现为出现相交、自相交拓扑异常。文献[14]提出基于事先预防的策略并结合Douglas-Peucker算法[15]对等高线进行拓扑一致性化简,但该方法需引入多个约束点从而导致图形冗余。文献[16, 17, 18]提出事后检测并消除拓扑异常的方法以保证拓扑一致性,但其判断拓扑异常的时间不是最优。文献[19]提出的扫描线算法是判断直线段相交的经典算法,文献[20]针对曲线上直线段首尾相连特点,提出了基于单调链的求交算法,其时间效率较扫描线算法进一步提升。
基于VS 2005平台开发了基于弯曲的曲线综合试验系统,试验数据为一组线状河流要素,以弯曲面积为综合指标,对河流要素进行多分辨率化简。曲线综合试验方案为:首先对曲线按本文方法建立弯曲多叉树并记录各弯曲的面积值,然后以综合后曲线节点数与原曲线节点数的比值作为压缩率,通过动态调整弯曲面积阈值大小,使得在删除所有小于弯曲面积阈值的弯曲后的曲线满足指定压缩率,最后对化简后的曲线按X轴方向建立单调链,采用文献[20]的基于单调链的求交算法来搜索相交、自相交拓扑异常,通过恢复节点来消除相交。
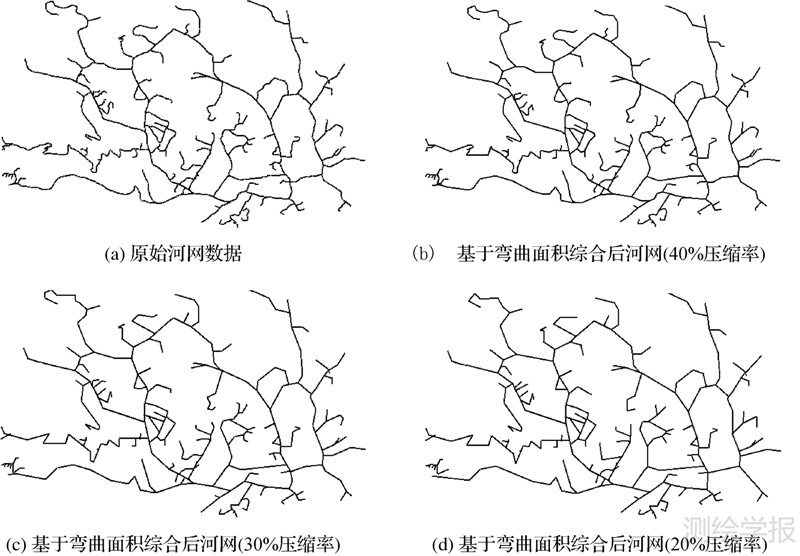
图 8为曲线综合前及其在40%、30%、20%压缩率下的综合后图形。随着弯曲删除数目的增多,曲线压缩率变高,综合后的曲线变平滑。因弯曲划分是相对于轴线的,而曲线轴线代表着曲线轮廓,对弯曲的删除操作不会使曲线偏离其轮廓,即使在20%的高压缩率下,综合后曲线仍保持着很高的图形相似度。
|
| 图 8 基于弯曲的曲线综合实例 Fig. 8 Example of line generalization based on curve bends |
曲线形态特征表现为弯曲间的相连、相对、嵌套,本文在弯曲的划分、提取与存贮结构等方面作了针对性研究,得出的结论有:① 基于曲线轴线划分的弯曲符合人视觉感受习惯,弯曲具有连续性、对称性和层次性;② 弯曲的层次化提取方法保证了复合弯曲先被提取,然后提取组成复合弯曲的子弯曲,通过弯曲分裂和坐标系变换可对不同方向、不同区间上的弯曲递归进行识别,对弯曲识别能力既强于约束Delaunay三角网法,又克服了拐点法、单调链法难以表达复合弯曲和识别结果敏感于个别线段走向的缺陷;③ 曲线轴线同时代表着曲线轮廓,随着弯曲分裂的深入,它会越来越逼近曲线,因弯曲划分是相对于轴线的,对弯曲的删除操作会使曲线向轴线逼近,综合后的曲线轮廓合理;④ 本文提出的多叉树结构具有很强的弯曲描述能力。较大尺寸的弯曲位于树的上层节点,较小尺寸的弯曲位于较低层节点,节点之间的父子、兄弟关系代表着弯曲间的嵌套、相邻等空间位置关系,通过弯曲的层次化提取方法可将曲线分解为一棵对应的弯曲多叉树。
| [1] | ZHU Guorui, GUO Lizhen, YIN Gongbai, et al. Map Design and Compilation [M]. Wuhan:Wuhan University Press,2001.(祝国瑞,郭礼珍,尹贡白,等.地图设计与编绘[M].武汉:武汉大学出版社,2001.) |
| [2] | WANG Z, MULLER J C. Line Generalization Based on Analysis of Shape [J]. Cartography and Geographic Information System, 1998, 25 (1):3-15. |
| [3] | PLAZANET C. Measurement Characterization and Classification for Automated Line Feature Generalization [C]// Proceedings of AutoCato. Bethesda:[s.n.], 1995:59-68. |
| [4] | ZHANG Qingnian, LIAO Ke. Line Generalization Based on Structure Analysis [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2001,40(5):118-121. (张青年,廖克.基于结构分析的曲线概括方法[J]. 中山大学学报:自然科学版, 2001,40(5):118-121.) |
| [5] | LUO Guangxiang, ZHU Guorui, WU Hehai, et al. The Study of the Model of Identifying Bends for Cartographic Linear Features Based on Analysing Coordinate Monotony [J]. Bulletin of Surveying and Mapping, 2005(10):21-24. (罗广详,祝国瑞,毋河海,等.坐标单调性分析下地图曲线弯曲识别模型的研究[J].测绘通报,2005(10):21-24.) |
| [6] | CHEN Huirong, PENG Rencan, ZHENG Yidong, et al. Coastline Generalization Based on Skeleton Line of Curve Bends [J]. Geomatics and Information Science of Wuhan University,2011,36(12):1418-1422. (陈惠荣,彭认灿,郑义东,等.以弯曲骨架线为化简指标的海岸线综合方法[J].武汉大学学报:信息科学版,2011,36(12):1418-1422.) |
| [7] | GUO Qingsheng, HUANG Yuanlin, ZHANG Liping. The Method of Curve Bend Recognition[J]. Geomatics and Information Science of Wuhan University,2008,33(6):596-599. (郭庆胜,黄远林,章莉萍.曲线的弯曲识别方法研究[J].武汉大学学报:信息科学版,2008,33(6):596-599.) |
| [8] | QIAN Haizhong, WU Fang, CHEN Bo, et al. Simplifying Line with Oblique Dividing Curve Method [J].Acta Geodaetica et Cartographica Sinica, 2007,36(4):443-449.(钱海忠,武芳,陈波,等.采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报,2007,36(4):443-449.) |
| [9] | AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Curve Hierarchical Structure in Depth [J]. Acta Geodaetica et Cartographica Sinica,2001,30(4):343-348. (艾廷华,郭仁忠,刘耀林.曲线弯曲深度层次结构的二叉树表达[J].测绘学报,2001,30(4):343-348.) |
| [10] | VAN DER POORTEN P M, JONES C B. Characterisation and Generalisation of Cartographic Lines Using Delaunay Triangulation [J]. International Journal of Geographical Information Science, 2002,16(8):773-794. |
| [11] | VAN DER POORTEN P M, SHENG ZHOU, JONES C B.Topologically-Consistent Map Generalisation Procedures and Multi-scale Spatial Databases [J].Lecture Notes in Computer Science, 2002, 2478:209-227. |
| [12] | ZHAI Renjian, WU Fang, ZHU Li, et al. Structured Representation of Curve Shape[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(2):175-182.(翟仁健,武芳,朱丽,等.曲线形态的结构化表达 [J].测绘学报,2009,38(2):175-182.) |
| [13] | GUO Qingsheng, LUE Xiuqin, CAI Yongxiang. Rule of the Spatial Topological Relation Abstraction in Graphic Simplification Process [J]. Geomatics and Information Science of Wuhan University, 2008, 33 (5):520-523.(郭庆胜,吕秀琴,蔡永香.图形简化过程中空间拓扑关系抽象的规律 [J].武汉大学学报:信息科学版,2008,33(5):520-523.) |
| [14] | ZHANG Chuanming, PAN Mao, WU Huanping, et al. Study on Simplification of Contour Lines Preserving Topological Coherence[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2007, 43(2):216-222.(张传明,潘懋,吴焕萍,等.保持拓扑一致性的等高线化简算法研究[J].北京大学学报:自然科学版,2007,43(2):216-222.) |
| [15] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Character [J]. The Canadian Cartographer, 1973,10(2):112-123. |
| [16] | CORCORAN P, MOONEY P, WINSTANLEY A. Planar and Non-planar Topologically Consistent Vector Map Simplification[J]. International Journal of Geographical Information Science, 2011, 25 (10):1659-1680. |
| [17] | CORCORAN P, MOONEY P, BERTOLOTTO M. Line Simplification in the Presence of Non-Planar Topological Relationships [C]//Lecture Notes in Geoinformation and Cartography:Bridging the Geographic Information Sciences. Avignon:Springer,2012:25-42. |
| [18] | SAALFELD A. Topologically Consistent Line Simplification with the Douglas-Peucker Algorithm [J]. Cartography and Geographic Information Science, 1999, 26(1):7-18. |
| [19] | BENTLEY J L, OTTMANN T A. Algorithms for Reporting and Counting Geometric Intersections [J]. IEEE Transactions on Computers, 1979, 28(9):643-647. |
| [20] | PARK S C, SHIN H. Polygonal Chain Intersection [J].Computers and Graphics, 2002, 26(2):341-350. |