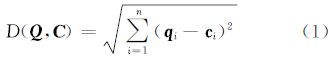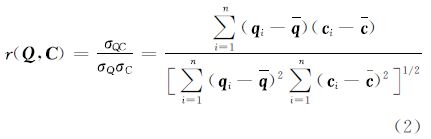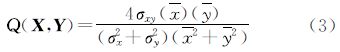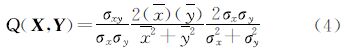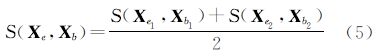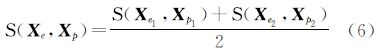2. 江苏北斗卫星应用产业研究院,江苏 南京 210032;
3. 南京工业大学 测绘学院,江苏 南京 210009
2. Jiangsu BDS Application Industry Institute,Nanjing 210032,China;
3. College of Geomatics Engineering,Nanjing University of Technology,Nanjing 210009,China
1 引 言
随着GPS接收机技术以及数据存储技术的不断发展,高频(1 Hz)和超高频(20~50 Hz)GPS接收机相继出现,同时单历元GPS处理技术亦逐渐成熟。GPS接收机被许多国内外学者作为一种“地震仪”来实时监测地壳运动,因此,一门新的前沿交叉学科--GPS地震学成为当前地震监测研究的热点[1, 2, 3, 4, 5, 6]。单历元高频GPS定位精度受跟踪GPS卫星数及分布情况、轨道误差、GPS和接收机钟差、大气延迟、天线相位偏差、多路径效应等众多因素影响[7, 8],其中很多影响因素都与GPS卫星-接收机的几何关系有关,因而可利用精确的GPS卫星运动周期来有效消除和减弱这些误差的影响。因GPS卫星重复周期约为一个恒星日,此滤波方法也称为恒星日滤波(sidereal filtering)。国内外学者对恒星日滤波及其应用进行大量研究,其中主要出发点是确定准确的GPS卫星重复周期,进而来削弱单历元定位噪声及分离多路径误差[9, 10, 11, 12, 13, 14]。
恒星日滤波的基本思想就是假设地震前后两天经过GPS卫星周期平移后的坐标时间序列的相关误差影响是相同的,理想情况下,震前、震中、震后3天数据的解算过程中,各时刻应采用相同的GPS卫星,相同的解算策略,解算相同的参数个数。但现实情况往往难以满足此条件,即使任何一颗GPS卫星的模糊度解算出现问题都可能导致最终的滤波出现较大的偏差;更极端的情况是,发生强震后由于地表建筑物等发生的巨大变化,地震前后两天的坐标时间序列大相径庭。这时仍然采用常规的恒星日滤波,非但无法提高精度,反而还可能会带来新的误差。文献[13]曾提出通过预处理观测数据等方法解决上述问题,但其计算工作量将十分巨大,而且极端的强震影响通过预处理也无法解决。
针对这一问题,本文提出一种顾及时间序列分段相似性的恒星日滤波优化算法,其基本思想是在构建滤波残差序列之前,首先确定用于构建滤波的坐标残差时间序列与地震当天坐标残差时间序列的相似性,根据相似性度量指标的大小确定权重后再进行滤波,滤波时设定一定的阈值,当相似度量指标低于该阈值时,该天的坐标残差时间序列将不参与构建滤波时间序列。
2 同震坐标时间序列的相似性分析 2.1 时间序列相似性定义时间序列相似性定义为[15]:给定两个时间序列Q={q1,q2,…,qn}和C={c1,c2,…,cn},如果dist(Q,C)≤α,就认为Q和C是相似的,其中dist(Q,C)是距离度量函数,比如欧氏距离;α是相似值阈值,用来调节相似程度。
时间序列的相似性分析是时间序列数据挖掘的基础问题,用于分析不同数据段之间的相似性和差异性,提取出有价值的信息。几乎所有的时间序列数据挖掘方法都和相似性分析有关,比如相似性搜索、聚类、分类、异常检测、分段和主题发现等。
2.2 时间序列相似性度量指标衡量两个时间序列之间的相似性一般通过距离或者相似性度量函数来衡量,相似性与距离成反比关系,距离越近越相似,否则越不相似[16]。众多学者已从不同的角度提出了多种距离或者相似性度量函数,距离函数主要有欧氏距离、动态弯曲距离、编辑距离等,相似性度量函数主要有余弦函数相似度、皮尔逊相关系数、通用影像质量评价指数。本文介绍其中比较常用的3个相似性度量指标。
2.2.1 欧氏距离(Euclidean distance,ED)欧氏距离[17]是时间序列相似性研究中最为广泛采用的相似性度量,其定义为
欧氏距离越短,表示序列之间越相似。但其最大的不足之处就是对时间轴上的偏移变化非常敏感,在进行相似性时间序列搜索时,时间轴上微小的偏差往往会导致搜索结果的错误。
2.2.2 皮尔逊相关系数(Pearson correlation coefficient,PCC)亦称简单相关系数,是统计学中常说的相关系数,它描述的是两个定距变量间联系的紧密程度。其定义为
式中,σQC为协方差;σQ、σC为标准差;q、c为时间序列的均值。相关系数的取值范围为[-1,1],-1表示全负相关,+1表示全正相关,0表示不相关。 2.2.3 通用影像质量评价指数(universal image quality index,UIQI)UIQI主要应用于影像质量评价,可认为是对皮尔逊相关系数的改进,其定义为[18]
此式可分解为
第1项即为相关系数,取值范围为[-1,1],当yi=axi+b(a、b为常数)时取最大值1或最小值-1;第2项是考虑序列的均值,取值范围为[0,1],当y=x时取最大值1,第3项是考虑序列的方差和协方差,取值范围为[0,1],当σy=σx时取最大值1。
从3个相似性度量的定义可以看出,欧氏距离越小表明相似性越高,而皮尔逊相关系数和UIQI绝对值越大相似性越高。
2.3 时间序列分段相似性的确定在研究地震同震形变时,其一般的研究对象是GPS站点坐标残差的时间序列,即站点坐标时间序列减掉坐标参考值后的残差序列[19, 20]。文中没有特殊说明的时间序列均指坐标残差时间序列。考虑到地震引起的形变,地震前后的站点坐标参考值分别通过地震发生前后一段时间的静态GPS观测得到。当地震发生时,地震波会导致站点的坐标时间序列出现较大的摆动波动,若直接求定地震前后的时间序列和地震当天序列的相似性,必然会造成相似性度量的不准确、不客观,同时也无法分辨强震导致震后相似性发生变化的情况。为解决该问题,本文提出采用分段相似性度量确定的方法,具体计算过程如下。
假定地震当天、前一天及后一天的坐标时间序分别为Xe(ti)、Xb(ti)和Xp(ti),(i=1,2,…,n),地震波到达的时刻为tk,持续历元为s,即tk~tk+s为受地震波影响的时间区间。根据地震波持续时间,将Xe(ti)、Xb(ti)和Xp(ti)分别划分为两段(根据实际情况可分为若干段)
根据分段后序列,分别求定每段时间序列间的相似性度量S:S(Xe1,Xb1)、S(Xe2,Xb2)、S(Xe1,Xp1)、S(Xe2,Xp2)。
一般情况下,地震前后两段时间序列的相似性基本相同,同时由于单历元定位误差的周期性,地震当天的时间序列与前后两天序列的相似性也基本相同,且会高于某一阈值ε,即
顾及分段相似性的恒星日滤波优化算法的基本思路,是在利用地震前后两天的时间序列构建滤波算子前,进行分段相似性度量的求定和判断,根据相似性度量S的大小进行定权,然后进行加权平均构建滤波时间序列。给定相似性度量的阈值ε,当时间序列的相似性度量低于ε时即认为不相关,不参与恒星日滤波的构建。具体相似性度量的情况及其处理方式总结见表 1所示。第4类情况即为发生强震的情况,由于无法分辨出环境发生变化的时刻,因而无法进行恒星日滤波。
| 情况分类 | 1 | 2 | 3 | 4 |
| S(Xe1,Xb1) | ≥ε | ≥ε | <ε | ≥ε |
| S(Xe2,Xb2) | ≥ε | ≥ε | <ε | <ε |
| S(Xe1,Xp1) | ≥ε | <ε | ≥ε | <ε |
| S(Xe2,Xp2) | ≥ε | <ε | ≥ε | ≥ε |
| 滤波处理方案 | 按照相似度加权平均震前后两天的序列 | 仅采用震前一天的序列滤波 | 仅采用震后一天的序列滤波 | 不能进行恒星日滤波 |
根据大量的试验统计和相关文献的研究结果[21],本文中对不同的相似性度量选取的阈值均为ε=0.5。由于不同的相似性度量的含义不同,对欧氏距离而言通过的是S≤0.5,而对皮尔逊相关系数和UIQI而言通过的则是|S|≥0.5。
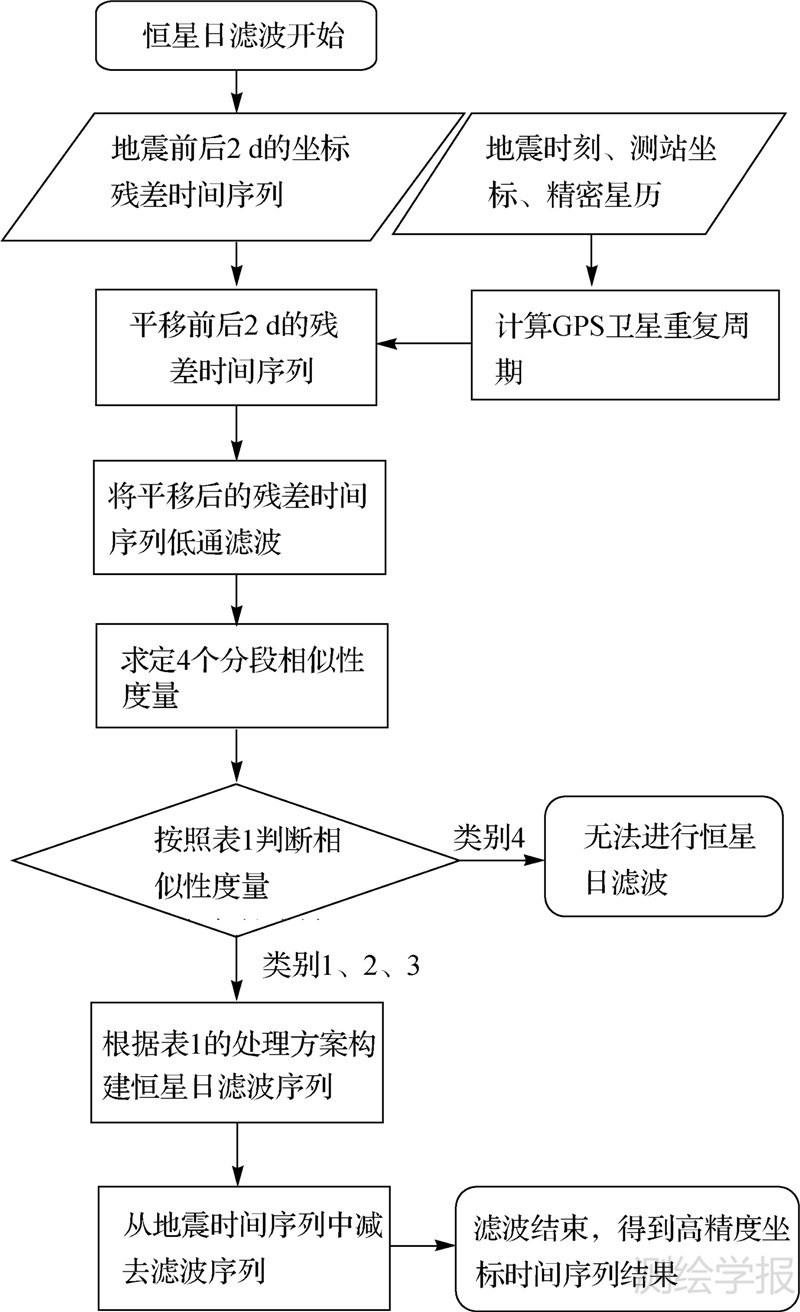
3.2 计算步骤根据上述基本思路,顾及分段相似性的恒星日滤波优化算法的具体计算步骤见图 1。
|
| 图 1 顾及分段相似性的恒星日滤波优化算法流程 Fig. 1 Process steps of improved sidereal filtering accounting for segments' similarity |
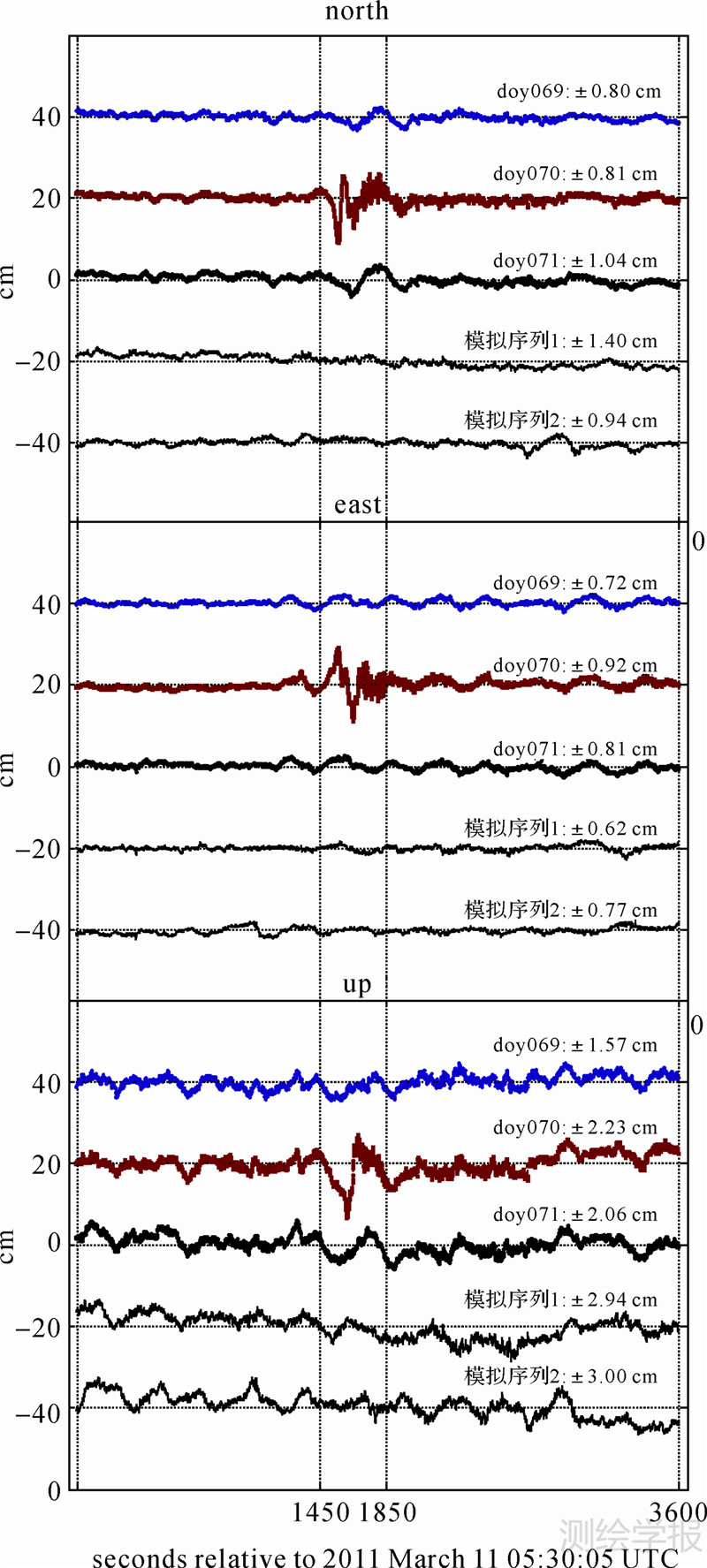
为评估相似性度量指标对恒星日滤波的影响,采用本文提出的方法对江苏省CORS网某GPS基准站的坐标残差时间序列进行滤波分析。试验数据对应的GPS年积日为2011年069、070和071 3 d,亦即2011年3月11日日本地震前后3 d的数据,069和071的时间序列已经根据计算得到的GPS卫星重复周期进行了相应平移。对站点071天N、E、U方向坐标残差时间序列分别加入了-4.0~4.0 cm区间的随机噪声,模拟GPS解算卫星、解算策略及解算参数个数不同等原因导致的定位误差或粗差。为了增强模拟算例的可靠性,模拟了两组不同的数据。站点3天各方向的坐标残差原始时间序列及加入噪声的时间序列见图 2所示。图中横轴坐标是相对于2011年3月11日UTC05∶30∶05的历元数。3个子图分别代表了N、E、U方向的时间序列,每个图中从上至下分别为年积日069、070、071、模拟数据一和模拟数据二的坐标残差时间序列,同时给出了坐标残差的中误差统计值。为了合理评定解算的中误差,在统计前先将发生地震时1450~1850历元的数据剔除。从图中可以明显看出,069、070和071 3 d的坐标残差时间序列的变化趋势非常相近,这也验证了前述周期性误差的存在,071天加入噪声后相似度明显降低。
|
| 图 2 站点3 d的坐标残差时间序列及第3天加入噪声的模拟序列 Fig. 2 Coordinate residual time series of 3 days and the 3th day's series with the simulation of the noise |
对这些坐标残差时间序列利用常规恒星日滤波以及分别采用欧氏距离、相关系数和UIQI等相似性度量的恒星日滤波优化算法进行处理。表 2为各种滤波处理后的坐标残差时间序列的统计。从表 2可以看出:
(1) 常规的恒星日滤波方法应对特殊情况的能力最差,滤波经常没有任何作用,如模拟算例1的N方向滤波前后精度保持不变;甚至有时会出现原始序列滤波后精度变差的情况,如模拟算例2的U方向精度从原始序列的±2.23 cm降低为滤波后的±2.56 cm。
(2) 顾及分段相似性的优化算法则大大改善了恒星日滤波的效果,提高了滤波的可靠性,特别是采用皮尔逊相关系数和UIQI作为相似性度量的优化算法,对于两个模拟算例都能得到满意的结果,且二者的精度相当。
(3) 选择欧氏距离作为相似性度量,虽然有时能够得到比较满意的结果,但有时精度较差,表现不稳定。
(4) 由于UIQI方法不仅顾及了时间序列间的相关系数,而且考虑了序列自身的均值和方差,因而本文建议采用UIQI作为恒星日滤波优化算法的相似性度量。
| cm | ||||||
| 恒星日滤波方法 | 模拟序列1 | 模拟序列2 | ||||
| N | E | U | N | E | U | |
| 滤波前定位精度 | ±0.81 | ±0.92 | ±2.23 | ±0.81 | ±0.92 | ±2.23 |
| 常规恒星日滤波 | ±0.81 | ±0.71 | ±1.78 | ±0.76 | ±0.74 | ±2.56 |
| 欧氏距离 | ±0.75 | ±0.68 | ±1.63 | ±0.71 | ±0.70 | ±2.34 |
| 皮尔逊相关系数 | ±0.64 | ±0.63 | ±1.43 | ±0.61 | ±0.61 | ±1.76 |
| UIQI | ±0.65 | ±0.63 | ±1.43 | ±0.61 | ±0.61 | ±1.76 |
本文将数据挖掘理论中的时间序列相似性分析引入恒星日滤波,提出了基于分段相似性度量的同震形变恒星日滤波优化算法,并研究了不同相似性度量指标对恒星日滤波优化算法的影响。研究结果表明,当由于GPS解算相关参数不同等原因引起解算误差较大或存在粗差时,或者强震后地表建筑物等发生了巨大变化而引起多路径效应等周期性误差发生根本性改变时,常规恒星日滤波非但不能起到提高精度的作用,有时还会适得其反。利用本文提出的顾及分段相似性度量的恒星日滤波优化算法则能有效克服传统恒星日滤波的缺点,大大提高了恒星日滤波的精度和可靠性。同时也发现,选择欧氏距离作为相似性度量的恒星日滤波算法精度不稳定;采用皮尔逊相关系数和UIQI作为相似性度量的优化算法,二者的精度较高且精度相当;由于UIQI方法不但顾及了时间序列间的相关系数,而且还考虑了序列自身的均值和方差,因而建议采用UIQI作为恒星日滤波优化算法的相似性度量。
| [1] | BILICH A, CASSIDY J F, LARSON K M. GPS Seismology: Application to the 2002 Mw 7.9 Denali Fault Earthquake[J]. Bulletin of the Seismological Society of America, 2008, 98(2): 593-606. |
| [2] | MENG Guojie, REN Jinwei, JIN Honglin, et al. Data Processing Methods of High Rate GPS and Its Application to Seismology[J]. Recent Developments in World Seismology, 2007(7): 613-620. (孟国杰, 任金卫, 金红林, 等. GPS高频数据处理方法及其在地震学中的应用研究进展[J]. 国际地震动态, 2007(7): 26-30.) |
| [3] | XU Caijun, LIU Yang, WEN Yangmao. Mw 7. 9 Wenchuan Earthquake Slip Distribution Inversion from GPS Measurements[J]. Acta Geodaetica et Cartographica Sinica,2009, 38(3): 195-201. (许才军, 刘洋, 温扬茂. 利用GPS资料反演汶川Mw 7. 9 级地震滑动分布[J].测绘学报, 2009, 38(3): 195-201.) |
| [4] | ZHONG Ping, DING Xiaoli, ZHENG Dawei, et al. Filter-based GPS Structural Vibration Monitoring Methods and Comparison of Their Performances[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 31-36. (钟萍,丁晓利,郑大伟,等. GPS结构振动监测数据滤波方法及其性能实验研究[J]. 测绘学报, 2007, 36(1): 31-36.) |
| [5] | BOCK Y. Continuous Monitoring of Crustal Deformation[J]. GPS World, 1991, 2(6): 40-47. |
| [6] | GENRICH J F, BOCK Y. Rapid Resolution of Crustal Motion at Short Ranges with the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(B3): 3261-3269. |
| [7] | HUANG Dingfa, DING Xiaoli, CHEN Yongqi, et al . Wavelet Filters Based Separation of GPS Multipath Effects and Engineering Structural Vibrations[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 36-41. (黄丁发, 丁晓利, 陈永奇, 等. GPS多路径效应影响与结构振动的小波滤波筛分研究[J]. 测绘学报,2001, 30(1): 36-41.) |
| [8] | XIONG Yongliang, DING Xiaoli, HUANG Dingfa, et al. Integrated Single Epoch Algorithm Based on Wavelet Transform and Its Application to Structural Vibration Monitoring [J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 202-207. (熊永良, 丁晓利, 黄丁发, 等. 基于小波变换的单历元算法及其在结构振动监测中的应用研究[J]. 测绘学报, 2005, 34(3): 202-207. |
| [9] | SEEBER G, MENGE F, VOLKSEN C, et al. Precise GPS Positioning Improvements by Reducing Antenna and Site Dependent Effects[C]//Advances in Positioning and Reference Frames. Berlin: Springer, 1997: 237-244. |
| [10] | PARK K D, NEREM R S, SCHENEWERK M S, et al. Site-specific Multipath Characteristics of Global IGS and CORS GPS Sites[J]. Journal of Geodesy, 2004, 77(12): 799-803. |
| [11] | CHOI K, BILICH A, LARSON M, et al. Modified Sidereal Filtering: Implications for High-rate GPS Positioning[J]. Geophysical Research Letters, 2004, 31(22): 1-4. |
| [12] | AGNEW D C, LARSON K M. Finding the Repeat Times of the GPS Constellation[J]. GPS Solutions, 2006, 11(1): 71-76. |
| [13] | LARSON K M, BILICH A, AXELRAD P. Improving the Precision of High-rate GPS[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B05): 1-11. |
| [14] | YIN Haitao, GAN Weijun, XIAO Genru. Modified Sidereal Filter and Its Effect on High-rate GPS Positioning[J]. Geomatics and Informaton Science of Wuhan University, 2011, 36(5): 609-611. (殷海涛, 甘卫军, 肖根如. 恒星日滤波的修正以及对高频GPS定位的影响研究[J]. 武汉大学学报: 信息科学版, 2011, 36(5): 609-611.) |
| [15] | FANG Jiaguo. Time Series Data Mining Based on Similarity Analysis[D]. Hangzhou: Zhejiang University, 2011. (方加果. 基于相似性分析的时间序列数据挖掘算法研究[D].杭州: 浙江大学, 2011.) |
| [16] | YANG Kang, LI Manchun, LIU Yongxue, et al. Accumulated Similarity Surface for Spatial Weights Matrix Construction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 259-265. (杨康, 李满春, 刘永学, 等. 基于累积相似度表面的空间权重矩阵构建方法[J].测绘学报, 2012, 41(2): 259-265.) |
| [17] | ZHANG Jun. Research on Data Mining Technology of Pattern-based Similarity Search in Time Series Database[D]. Nanjing: Southeast University, 2006. (张军. 基于时间序列相似性的数据挖掘方法研究[D]. 南京: 东南大学, 2006.) |
| [18] | WANG Z, BOVIK A C. A Universal Image Quality Index[J]. IEEE Signal Processing Letters, 2002, 9(3): 81-84. |
| [19] | FANG Rongxin, SHI Chuang, GU Shengfeng. Precise Point Positioning with High-rate GPS Data Applied to Seismic Displacements Analysis[J]. Geomatics and Informaton Science of Wuhan University, 2009, 34(11): 1340-1343. (方荣新, 施闯, 辜声峰. 基于PPP动态定位技术的同震地表形变分析[J]. 武汉大学学报: 信息科学版, 2009, 34(11): 1340-1343.) |
| [20] | FANG Rongxin. High-rate GPS Data Non-difference Precise Processing and Its Application on Seismology[D]. Wuhan: Wuhan University, 2010. (方荣新. 高采样率GPS数据非差精密处理方法及其在地震学中的应用研究[D]. 武汉: 武汉大学, 2010.) |
| [21] | ZHANG Qian, WANG Zhihe, ZHANG Guozhi. An Algorithm for Discovering Positive and Negative Association Rules Based on Correlation Coefficient[J]. Journal of Shanxi University of Technology, 2005, 21(4): 35-38. (张倩, 王治和, 张国治. 基于相关系数的正、负关联规则挖掘算法[J]. 陕西理工学院学报, 2005, 21(4): 35-38.) |