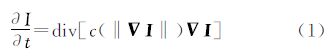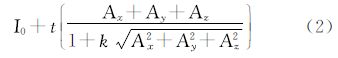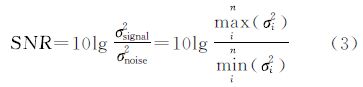1 引 言
地面激光扫描技术获取的激光点云不仅具有完整的三维空间信息,而且包含丰富的激光反射强度信息。通过对点云强度信息的处理和增强,有助于对不同类型的目标进行准确分割和识别。
激光强度信号受到各种因素影响而产生噪声,主要是高斯噪声和椒盐噪声[1]。高斯噪声是因激光发射、接收和大气传输等因素影响而产生的噪声,对强度反射特征的改变满足高斯分布规律,通过线性滤波方法可以有效抑制。椒盐噪声是因目标表面特定区域的反射特性(如不同材质或不同粗糙度),形成幅值近似相等但孤立而随机地分布在不同位置上,且均值不为0的噪声。椒盐噪声属于高频信息,常常与点云上的激光强度边缘和细节等高频信息混合在一起而难以区分,非常不利于目标区域的分割和识别。线性滤波的低通特点往往在滤波的同时也破坏了点云中的重要边缘和细节特征。
在图像处理领域,椒盐噪声的滤波方法主要有加权中值滤波[2, 3]、方向中值滤波[4, 5]、自适应滤波[6, 7]、各向异性扩散滤波[8, 9, 10]等方法。这些方法均能在消除图像椒盐噪声的同时,不同程度地保持图像边缘等细节特征。其中各向异性扩散滤波的保边缘特性尤为明显[11]。在SAR图像滤波领域,基于信噪比的自适应滤波[12]和基于特征保持的线性滤波[13]都能很好地保留雷达图像的纹理结构信息。在激光强度数据滤波方面,目前仅在成像激光雷达滤波[14, 15, 16]和机载Lidar强度滤波[17, 18]中有相关研究。文献[15]提出一种基于多级非线性加权平均中值滤波的散斑噪声抑制方法,并进行仿真试验。文献[17]提出一种融合强度图像像元邻域高程信息的均值滤波方法,该文主要考虑顾及地形平滑度的强度去噪,并未涉及椒盐噪声的滤波。文献[18]利用各向异性扩散方法进行强度滤波研究。该文献并没有给出详细的滤波算法,而是直接利用第三方图像处理工具包进行试验。无论是成像激光雷达滤波,还是机载LiDAR强度滤波,处理对象都是二维规则图像,并不直接对点云数据进行操作。但地面激光扫描通常获取360°空间范围内的各种地物,空间分布较为复杂,点云分辨率随距离和方位都呈现非线性改变,点的排列并不完全规则,将三维点云投影为二维图像难以避免像元重叠或者像元空洞的问题。另一方面,点云通常都会经过配准或地理坐标系转换等处理,此时投影中心已发生变化,成像几何关系难以恢复。因此,对于地面激光点云,采取图像的滤波方式并不合适。
本文针对地面激光扫描点云数据排列不规则、分布复杂的特点,以强度噪声滤波和边缘保持为目的,按照扩散滤波的原理,构造出点云强度的三维扩散滤波方程。通过研究扩散方程参数的性质和对比试验,分析并验证本文滤波方法的正确性。
2 扩散滤波原理基于扩散方程的滤波方法是一种非线性滤波技术,它是从物理中的扩散现象演绎而来。在扩散方程中设计合适的扩散系数来控制扩散方程的扩散行为,使得滤波过程可以缓慢而稳健地处理高频信息。为了防止扩散效应对边缘和细节的影响,根据扩散梯度值引入了一个边缘截止函数c(·)来改变扩散率。扩散的偏微分方程[19]为
式中,div[·]为散度算子;▽I是灰度梯度向量;c‖▽I‖为边缘截止函数,是灰度梯度向量▽I的非负单调递减函数;t是扩散时间(或扩散次数)。定义边缘截止函数c‖▽I‖=exp-(▽I2/k2)。k是边缘强度域的尺度参数。扩散方程在不同的方向上自动产生该方向上梯度的单调递减函数作为扩散系数。因此在同质区域内部,灰度值变化不大,梯度较小,于是它的扩散系数较大,可以有效地平滑同质区域内的噪声。而在边缘和细节部分,灰度值变化剧烈,梯度较大,扩散系数就较小,就能够保留边缘和细节信息。
3 点云强度三维扩散滤波方程的建立扩散方程要求对当前滤波点进行邻域方向梯度计算。邻域方向梯度计算在二维图像中比较容易实现,即对图像上相邻行列号的像元计算方向梯度。机载激光扫描点云通常沿平面分布,也可以通过二维投影的方法得到机载激光强度图像,按照图像邻域的构造方法间接得到点云的邻域和方向梯度。但是对于地面激光扫描点云,其空间分布的不规则性和不均匀性,难以用规则二维图像的邻域关系计算方向梯度,必须根据点云邻域的自身特点重新构造方向梯度的计算方法。
首先需要快速查找点云邻域。本文采用KNN算法[20, 21]建立点云的邻域集。若考察点P的激光强度为I,邻域集为Qi,对应强度值为Ii(i=1,2,…,n)。那么定义P点强度梯度为
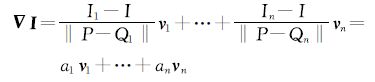
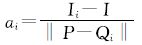
显然,强度梯度是定义在邻域点集内的所有方向上。由于点云散乱不规则,每一点的单位方向向量都不一致,每一点的梯度向量的维数也不同。为了在整个点云中进行统一表示,将任意方向向量投影到空间直角坐标向量上表达
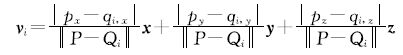
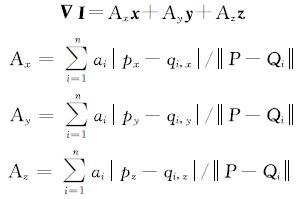
点云中各点强度梯度向量构成一个向量场,可以进一步得到强度梯度向量场的散度。散度是一个标量,其数值大小直接反映了梯度向量场中该点单位面积内发散(或汇集)梯度向量线的程度。在强度边缘处的梯度比较大,梯度变化也较大,所以位于边缘上的点的强度散度也比较大,而在平坦部分散度接近于0。因而定义P点强度梯度的散度为
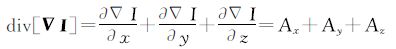
取边缘截止函数的简化形式c‖▽I‖=1/(1+k|▽I|),经过t次扩散后,P点强度为
式(2)就是激光点云强度的三维扩散滤波方程。其中参数Ax、Ay、Az由确定的邻域点集计算得到,与激光强度原始值I0同为点云的本征参数。扩散过程则由尺度参数k和扩散次数t控制。
激光点云强度噪声的三维扩散滤波算法步骤如下:
(1)计算待滤波点的k-邻域。
(2)逐一计算待滤波点和k-邻域集合中点的距离和强度差,形成强度梯度。
(3)根据三维扩散滤波方程,更新待滤波点的强度值。
(4)重复步骤(2)和步骤(3),直到满足强度值不发生改变。
4 试验及分析本文选取由Leica HDS6000地面激光扫描仪获取的某建筑物立面点云作为试验数据。该建筑物表面具有比较明显的不同反射特征区域和平面转折区域,具备了多种边缘和细节特征。点云数据的空间分辨率为2 cm,足够表达建筑物上的几何边缘。其强度量化等级为12 bit,具有很高的强度分辨率,可以表达数据中极其微小的反射特征差异和强度噪声。滤波算法是在Microsoft Visual Studio 2010编译环境下,利用C++语言,结合OpenGL进行编程实现。
为了验证强度扩散滤波方程,首先需要考虑的是如何评价滤波质量。点云中的边缘和细节区域具有最大信息量,强度统计为最大方差,噪声区域信息量极小,强度统计为最小方差,完全同质区域无信息量,方差为零。因此,本文采用信噪比作为评价手段。所用的信噪比计算方法为局部最小方差法[22],将点云局部强度方差的最大值作为信号方差,非零最小值作为噪声方差,其定义式[23]为
在试验进行的过程中,强度滤波和信噪比计算都依赖于邻域计算,因此邻域点数n的取值十分关键。n值过小,不具备统计意义,信噪比的计算不可靠。n值过大,邻域点过多,无法真实反映边缘和细节信息。在三维空间中,平面点的最小邻域点数n=8,二面相交棱上点的最小邻域点数n=8,三面相交交点的最小邻域点数n=6,因此邻域n值的最小分布范围应为[6, 8]。不失一般性,本文试验中取n=8。
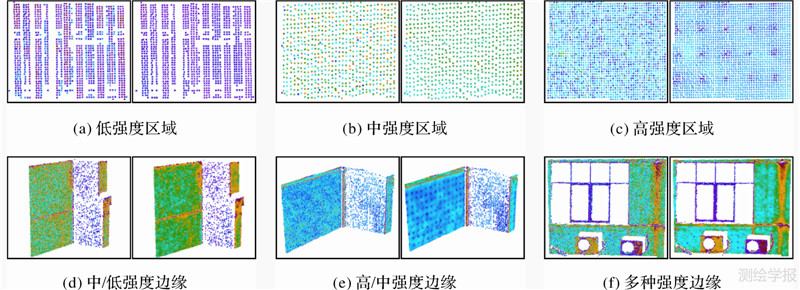
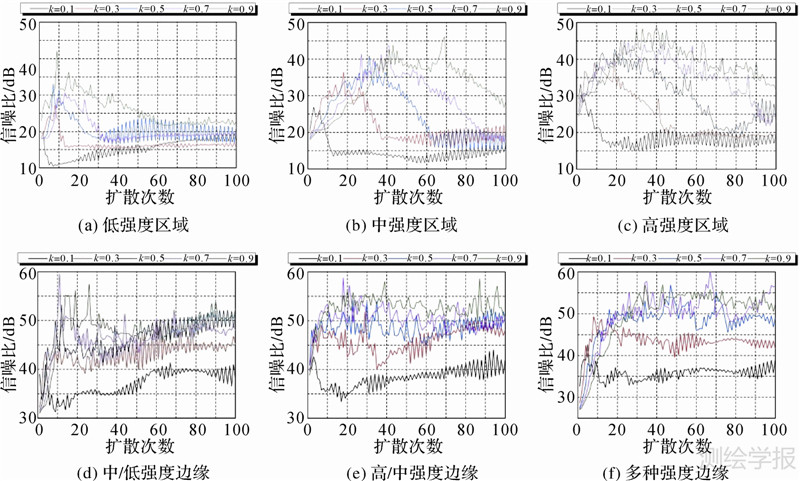
图 1中是6类试验点云,分别是低强度区域、中强度区域、高强度区域、中/低强度边缘、高/中强度边缘、多种强度边缘。每一区域中都含有噪声点云。根据扩散方程,扩散结果主要依赖于扩散尺度k的选择,因此需要重点考察不同扩散尺度对扩散后点云信噪比的影响规律,从而确定合适的扩散尺度。分别对这6类试验点云选取k=0.1、k=0.3、k=0.5、k=0.7、k=0.9进行100次扩散滤波,计算滤波的每一次点云信噪比,统计并绘制信噪比曲线(图 2)。
|
| 图 1 扩散滤波前后点云数据对比(k=0.9) Fig. 1 Comparison of point cloud before and after diffusion filtering |
|
| 图 2 点云信噪比随扩散次数的变化 Fig. 2 SNR of point cloud changes with diffusion times |
对图 2进行分析,可以发现以下特点:
(1) 信噪比曲线总体呈现先快速上升、后逐渐衰减的趋势,存在一个信噪比峰值。表明扩散方程在上升区间消除了强度噪声,而在衰减区间削弱了强度边缘。信噪比峰值对应的扩散次数可以作为滤波结束的条件。
(2) 信噪比曲线峰值的出现位置受扩散尺度控制。扩散尺度越小,信噪比达到峰值的扩散次数越小。
(3) 信噪比曲线峰值的大小也受扩散尺度控制。扩散尺度越大,信噪比峰值越大。
(4) 信噪比曲线在衰减区局部存在明显的振荡。这是因为在三维扩散滤波方程的本征参数中,包含一个Ii-I的表达,因此强度更新有正有负。当点云中不存在椒盐噪声后,滤波就仅仅表现为邻域内部强度信息的循环式扩散。
可见,扩散尺度在点云强度的扩散滤波中具有重要作用。扩散尺度太小,滤波后信噪比比较低,不利于边缘和细节特征的保持。扩散尺度较大时,信噪比峰值对应的滤波次数较大,滤波过程较长。因而在可容忍的扩散时间内选择较大的扩散尺度因子,用时间效率换取滤波质量,可以达到较好的滤波效果。此外,信噪比在扩散滤波中也具有积极作用。信噪比不仅可以作为扩散滤波效果的评价因子,还可作为滤波处理的结束条件。
为了进一步说明扩散滤波方程的效果,将中值滤波与其进行比较。中值滤波也是一种典型的非线性滤波,在点云中的处理方式是将邻域点云的强度进行排序,取序列中点的强度值代替待滤波点的强度值。
图 3是对3种包含边缘和细节信息的局部点云进行扩散滤波与中值滤波后的点云对比。很明显,中值滤波在去除噪声的同时,也削弱了主要边缘和细节。而本文的扩散滤波方程很好地保留了这些重要信息。

|
| 图 3 点云扩散滤波与中值滤波后边缘和细节对比(k =0.9) Fig. 3 Edge and detail comparison between diffusion filtering and median filtering |
表 1列出了两种方法对6类不同区域和全部点云进行滤波后的信噪比比较。从定量数值的比较中可以看出,两种方法都一定程度提高了信噪比,而扩散滤波方法要更优于中值滤波。
| 试验数据 | 低强度区域 | 中强度区域 | 高强度区域 | 中/低强度边缘 | 高/中强度边缘 | 多种强度边缘 | 全部点云 | |
| 信噪比/dB | 滤波前 | 16.99 | 17.26 | 23.58 | 30.55 | 36.05 | 26.66 | 53.61 |
| 中值滤波 | 37.22 | 37.75 | 37.39 | 54.51 | 56.69 | 54.47 | 72.43 | |
| 扩散滤波 | 42.02 | 46.04 | 48.75 | 57.43 | 57.99 | 56.82 | 77.94 | |
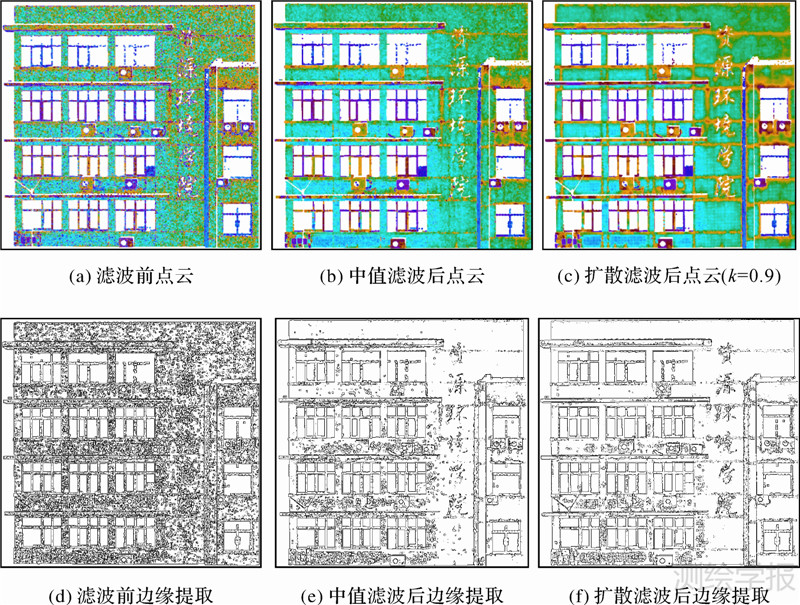
图 4是对全部点云进行扩散滤波与中值滤波后点云和边缘提取效果的对比。从对比中不难看出,滤波前噪声明显,边缘提取效果较差。中值滤波后得到一定改善,但细小边缘仍然较多,部分主要边缘也不明显。扩散滤波后效果较好,细小边缘明显减少,主要边缘更为明显,说明对同质区域的激光反射强度恢复能力强,更有利于进一步的区域分割和识别提取。
|
| 图 4 扩散滤波与中值滤波后点云和边缘提取效果对比 Fig. 4 Comparison of point cloud and edge extraction between diffusion filtering and median filtering |
本文将扩散滤波思想应用到点云强度滤波中,在点云邻域基础上研究强度的梯度和散度表达式,推导建立了点云强度的三维扩散滤波方程。深入分析了扩散尺度对滤波性能的影响,结合信噪比对滤波效果进行定量评价,进而为扩散滤波尺度参数的最优选择和收敛条件的设定提供了客观依据。通过试验对比,证实了本文方法在激光点云强度滤波过程中的去噪保边缘能力。
本文的工作主要集中在扩散尺度和滤波性能对比方面,而边缘截止函数的选择对滤波也具有一定影响,目前在光学图像处理、SAR图像处理、地震三维数据处理领域都是研究热点。因而在本文研究基础上,也有必要研究更为适用于点云强度数据的边缘截止函数,从而进一步提高点云数据质量。
| [1] | LI Ziqin, LI Qi, WANG Qi. Noise Characteristic in Active Laser Imaging System by Statistic Analysis[J]. Chinese Journal of Lasers, 2004, 31(9): 1081-1085. (李自勤, 李琦, 王骐. 由统计特性分析激光主动成像系统图像的噪声性质[J]. 中国激光, 2004, 31(9): 1081-1085.) |
| [2] | CHEN Yong, SHEN Yongzeng, JI Jiangbing, et al. A New Fast Weighted Median Filtering Algorithm[J]. Computer Engineering, 2003, 29(3): 89-90. (陈勇, 沈永增, 计建炳, 等. 一种新的加权中值滤波的快速算法[J]. 计算机工程, 2003, 29(3): 89-90.) |
| [3] | LI Xunbo, JIANG Dongsheng, WANG Zhenlin. Weighted Median Filtering of Im Based on Grads Similarity[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(1): 114-119. (李迅波, 蒋东升, 王振林. 梯度相似性的椒盐图像加权中值滤波算法[J]. 电子科技大学学报, 2012, 41(1): 114-119.) |
| [4] | FENG Xingkui, XIAO Xingming, YIN Hongjun. The Directional Medial Filtering with Weights[J]. Journal of Image and Graphics, 2000, 5(7): 609-611. (冯星奎, 肖兴明, 尹洪君. 方向加权中值滤波算法[J]. 中国图象图形学报, 2000, 5(7): 609-611.) |
| [5] | CZERWINSKI R N, JONES D L, O’BRIEN W D. Ultrasound Speckle Reduction by Directional Median Filtering[C]//Proceedings of International Conference on Image Processing. Washington D C: IEEE, 1995: 358-361. |
| [6] | LI Shutao, WANG Yaonan. Non-Linear Adaptive Removal of Salt and Pepper Noise from Images[J]. 2000, 5(12): 999-1001. (李树涛, 王耀南. 图像椒盐噪声的非线性自适应滤除[J]. 中国图象图形学报, 2000, 5(12): 999-1001.) |
| [7] | ZHAO Chunhui, HUI Junying, WANG Wei, et al. A Class of Adaptive Ranked-order Morphological Filters[J]. Journal of Image and Graphics, 2000, 5(8): 674-677. (赵春晖, 惠俊英, 王伟, 等. 一类自适应顺序形态滤波器[J]. 中国图象图形学报, 2000, 5(8): 674-677.) |
| [8] | MA Jie, YAN Jiabin, LIU Guizhong, et al. Anisotropic Diffusion Smoothing of Mixed Noise[J]. Journal of Central South University: Science and Technology, 2010, 41(1): 231-237. (马捷, 严家斌, 刘贵忠, 等. 混合噪声的各向异性扩散平滑[J]. 中南大学学报: 自然科学版,2010, 41(1): 231-237.) |
| [9] | BAI Jian, FENG Xiangchu. Fractional-order Anisotropic Diffusion for Image Denoising[J]. IEEE Transactions on Image Processing, 2007, 16(10): 2492-2502. |
| [10] | CHEN Shoushui, YANG Xin.A New Adaptive Diffusion Equation for Image Noise Removal and Feature Preservation[C]//ICPR '06 Proceedings of the 18th International Conference on Pattern Recognition: 3. Washington: IEEE, 2006: 885-888. |
| [11] | ZHANG Chunxiao, ZHAO Yan, LIAN Yuanfeng. Research on Anisotropic Diffusion Denoising Development[J]. Electronics Optics&Control, 2012, 19(5): 51-55. (张春晓, 赵剡, 连远锋. 各向异性扩散图像去噪现状研究[J]. 电光与控制, 2012, 19(5): 51-55.) |
| [12] | SUN Qian, ZHU Jianjun, LI Zhiwei, et al. A New Adaptive InSAR Interferogram Filter Based on SNR[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 437-442. (孙倩, 朱建军, 李志伟, 等. 基于信噪比的InSAR干涉图自适应滤波[J]. 测绘学报, 2009, 38(5): 437-442.) |
| [13] | YANG Shenbin, LI Bingbai, SHEN Shuanghe, et al. Structure Retaining Linear Multi-channel SAR Image Speckle Filte[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 364-370. (杨沈斌, 李秉柏, 申双和, 等. 基于特征保持的线性多通道最优求和SAR图像滤波算法[J]. 测绘学报, 2006, 35(4): 364-370.) |
| [14] | JIANG Lihui, ZHAO Chunhui, WANG Qi. Algorithm about Suppressing Speckle Noise in Coherent Laser Radar Imagery[J]. Acta Optica Sinica, 2003, 23(5): 541-546. |
| [15] | JIANG Lihui, ZHAO Chunhui. Speckle Noise Suppressing Based on Multilevel Nonlinear Weighted Mean Median Filter[J]. Laser & Inferared, 2003, 33(5): 380-382. |
| [16] | LI Ziqin, WANG Qi, LI Qi, et al. Comparison of Algorithms for Suppressing Speckle in Laser Imaging System[J]. Infrared and Laser Engineering, 2003, 32(4): 130-133. |
| [17] | LAI Xudong, ZHENG Xuedong, WAN Youchuan. A Kind of Filtering Algorithms for Lidar Intensity Image Based on Flatness Terrain[C]//Proceedings of International Symposium on Spatio-temporal Modeling, Spatial Reasoning, Analysis, Data Mining and Data Fusion. Beijing: [s.n.], 2005. |
| [18] | NOBREGA R A A, QUINTANILHA J A, O’HARA C G. A Noise-removal Approach for Lidar Intensity Images Using Anisotropic Diffusion Filtering to Preserve Object Shape Characteristics[C]//ASPRS 2007 Annual Conference.Tampa: Acta Press, 2007. |
| [19] | PERONA P, MALIK J. Scale-space and Edge Detection Using Anisotropic Diffusion[J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 1990, 12(7): 629-639. |
| [20] | ANDREWS L. A Template for the Nearest Neighbor Problem[J]. C/C++ Users Journal, 2001, 19(11): 40-49. |
| [21] | ARYA S, MOUNT D M, NETANYAHU N S, et al. An Optimal Algorithm for Approximate Nearest Neighbor Searching in Fixed Dimensions[J]. Journal of the ACM, 1998, 45(6): 891-923. |
| [22] | ZOU Mouyan. Deconvolution and Signal Recovery[M]. Beijing: National Defence Industry Press, 2004:186-188. (邹谋炎. 反卷积和信号复原[M]. 北京: 国防工业出版社, 2004: 186-188.) |
| [23] | WANG Xuewei, WANG Chunxin, ZHANG Yuye. Research on SNR of Point Target Image[J]. Electronics Optics & Control, 2010, 17(1): 18-21. (王学伟, 王春歆, 张玉叶. 点目标图像信噪比计算方法[J]. 电光与控制, 2010, 17(1):18-21.) |