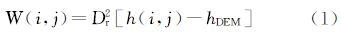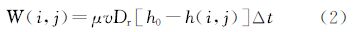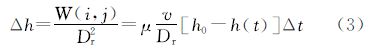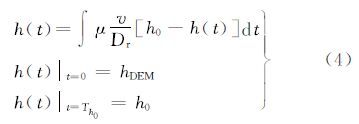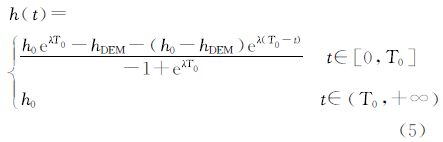2. 西南交通大学 地球科学与环境工程学院,四川 成都 610000;
3. 香港中文大学 霍英东遥感所,香港 999077
2. Faculty of Geosciences and Environmental Engineering,Southwest Jiaotong University,Chengdu 610000,China;
3. Fok Ying Tung Remote Sensing Science Building,The Chinese University of Hong Kong,Hong Kong 999077,China
1 引 言
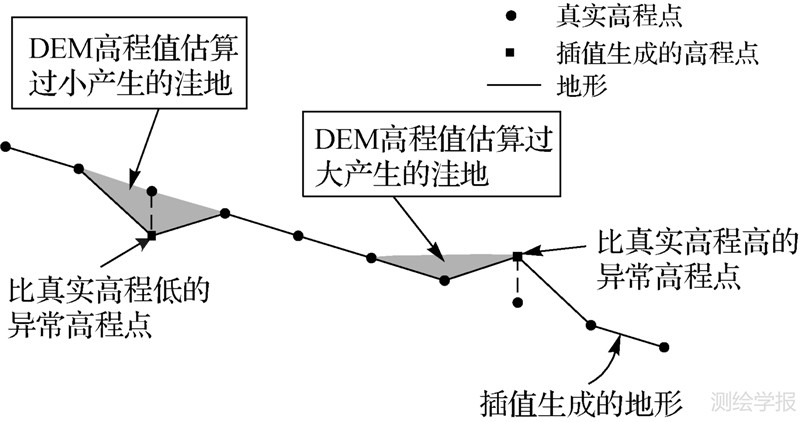
洪水淹没分析是准确提取洪水淹没范围、水深及历时等灾情信息的关键,作为灾前洪水预警预报和灾中洪水灾害评估的技术支持,在防洪抢险、救灾、减灾辅助决策过程中发挥着重要的作用。洪水淹没分析的实质是分析计算给定水位下,洪水在地理空间上的蔓延过程及淹没范围、淹没水深和造成的受灾程度。虽然严密的水文-水动力方法能够准确计算洪水淹没范围[1, 2, 3],但是由于水文水力学模型建模复杂,且受计算条件、数据观测与采集手段的限制,其实用性有限。针对灾害应急响应过程中灾情快速评估的需求以及数据不完备的情况,利用数字地形分析技术进行洪水淹没分析因其原理简单及数据需求低的特点,而成为普遍采用的方法[4, 5, 6, 7, 8, 9, 10, 11]。数字地形分析结果的可靠性和准确性主要受DEM格网分辨率以及高程精度等的限制,比如由于高程异常导致伪洼地(图 1)和平地的出现,而水流在洼地区域的不连续性以及在平地区域的不确定性、随意性使得格网点处水流流向的判定出现不确定性,因此对洼地的处理成为DEM水文分析的焦点问题之一[12]。传统的洪水淹没分析方法对洼地一般采用统一高程进行填洼处理[12, 13, 14, 15],反而造成许多相邻格网点具有相同高程,产生洪水流向新的不确定性[16, 17, 18, 19, 20]。为此,在对DEM上某一点进行流向追踪时,常采用其前向节点水位减去一个修正值作为参考水位的水位修正方法,该方法中水位修正值是依据地形高程值的变化率确定的。当整个地形的变化率基本恒定时,可以依据地形高程的整体变化率计算得到一个恒定的水位修正值。但是由于真实地形起伏导致高程变化率并非是一个恒定值,所以恒定水位修正值方法在实际使用过程中存在两个主要缺陷,即在高程变化率较大的区域将出现水面爬坡现象(图 2);以及在变化率较小的区域就会因为衰减太快而出现自阻断流现象,难以找到一个合适的恒定水位修正值。
|
| 图 1 洼地产生剖面图图解:由DEM高程值估算过小或过大产生的洼地 Fig. 1 Two-dimensional illustration of spurious depressions along valley bottom arising from underestimated elevation and from overestimated elevation |
|
| 图 2 自然水面与爬坡水面对比(自然水面局部水平,爬坡水面效果是水面边缘往坡上延伸,致边缘水位高于内侧水位) Fig. 2 Comparison between natural water and up-lifting of water |
针对上述问题,依据洪水演进规律,本文提出自适应逐点水位修正算法,在充分考虑水流速度和淹没时间的基础上计算水位修正值,克服恒定水位修正值带来的爬坡和断流现象,在此基础上确保准确计算洪水淹没范围、水深和洪水历时等模拟结果。
2 自适应逐点水位修正的种子点蔓延算法 2.1 淹没分析算法流程洪水淹没分析的基本算法之一是种子点蔓延算法。种子点蔓延是指在区域选定种子点,赋予特定的属性和作用规则,然后沿“四向连通区域”或“八向连通区域”蔓延扩散,将该属性和作用规则扩展到整个区域。利用种子点蔓延算法进行淹没分析,就是按给定水位条件,求取符合数据采集分析精度,且具有连通关联分布的点的集合,该集合计算得到连续平面就是要估算的淹没区范围,而满足水位条件,但与种子点不具备连通关联性的其他连续平面,将不能进入集合区内。该方法的主要特点是能充分考虑到“流通”淹没的情形,即洪水只能淹没它能流到的地方,较适合因上游来水(例如决堤)、洼地溢出水(例如局部暴雨引起的暴涨洪水向四周扩散)引起的淹没分析。传统的种子点蔓延分析方法中,洪水淹没过程仅考虑地形起伏,对淹没区内所有淹没点的水位采取同一值,并未考虑洪水的蔓延与扩散是与流速和淹没时间密切相关的,洪水淹没分析结果可靠性低。
如图 3所示,顾及洪水淹没的实际情况,本文方法的起始淹没点位置一般选在蓄滞洪区入口或者堤防溃决口处邻近的网格内,以该网格为种子点向外遍历其8邻域网格,将满足淹没条件的网格存入淹没缓存区,并不断迭代计算,直至获取整个淹没区范围。其中,网格淹没判断的条件为:① 是否与已淹没网格相邻;② 网格平均高程是否低于当前种子点修正后的水位。在种子点向外扩散过程中,如果对淹没区内所有的网格进行扩散计算,会降低洪水演进计算的效率,因此,本算法对淹没区边界网格和淹没区域内部网格采用不同的处理策略:对于淹没区的边界网格,将其视为新的种子点,进行新一轮的扩散计算;对于淹没区内部的网格,则在自适应水位修正的基础上,计算更新该网格的水深、历时等信息。
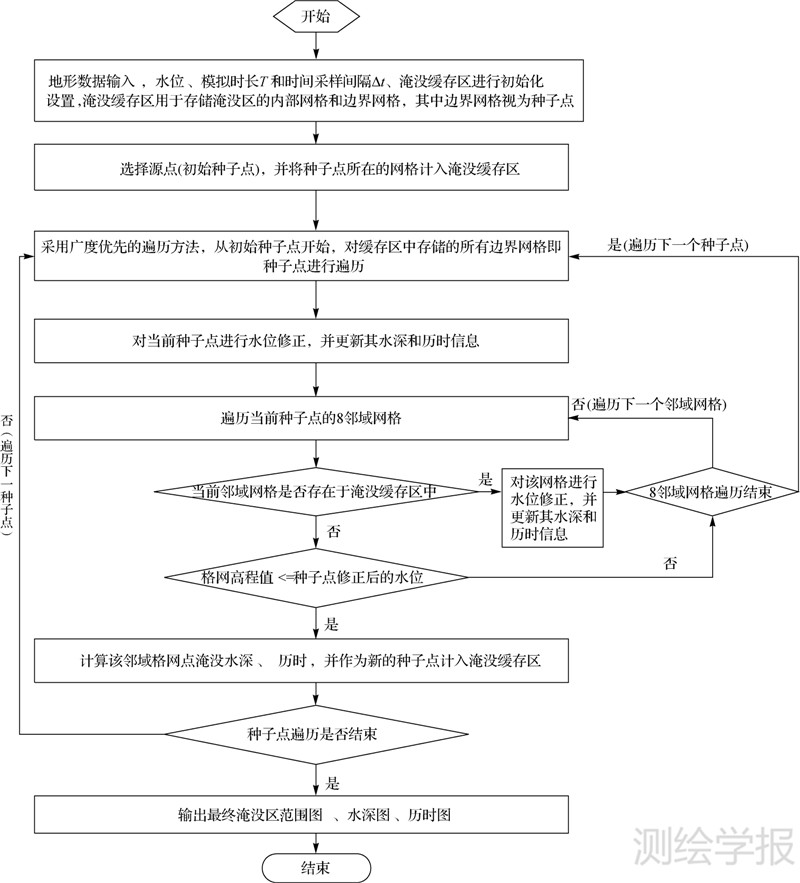
|
| 图 3 洪水淹没分析流程图 Fig. 3 Flow chart of the flooding analysis algorithm |
上述方法的核心是自适应的逐点水位修正。为了实现逐点水位修正,本文提出拟合洪水水位值的“体积法”(图 4),其基本思想是:根据洪水由高向低流动的重力特性和地形起伏情况,用洪水水量(由于漫堤或溃口流进城区或蓄滞洪区的洪水水量)与洪水淹没范围内总水量体积相等的原理来模拟洪水淹没范围[21, 22, 23, 24, 25, 26]。
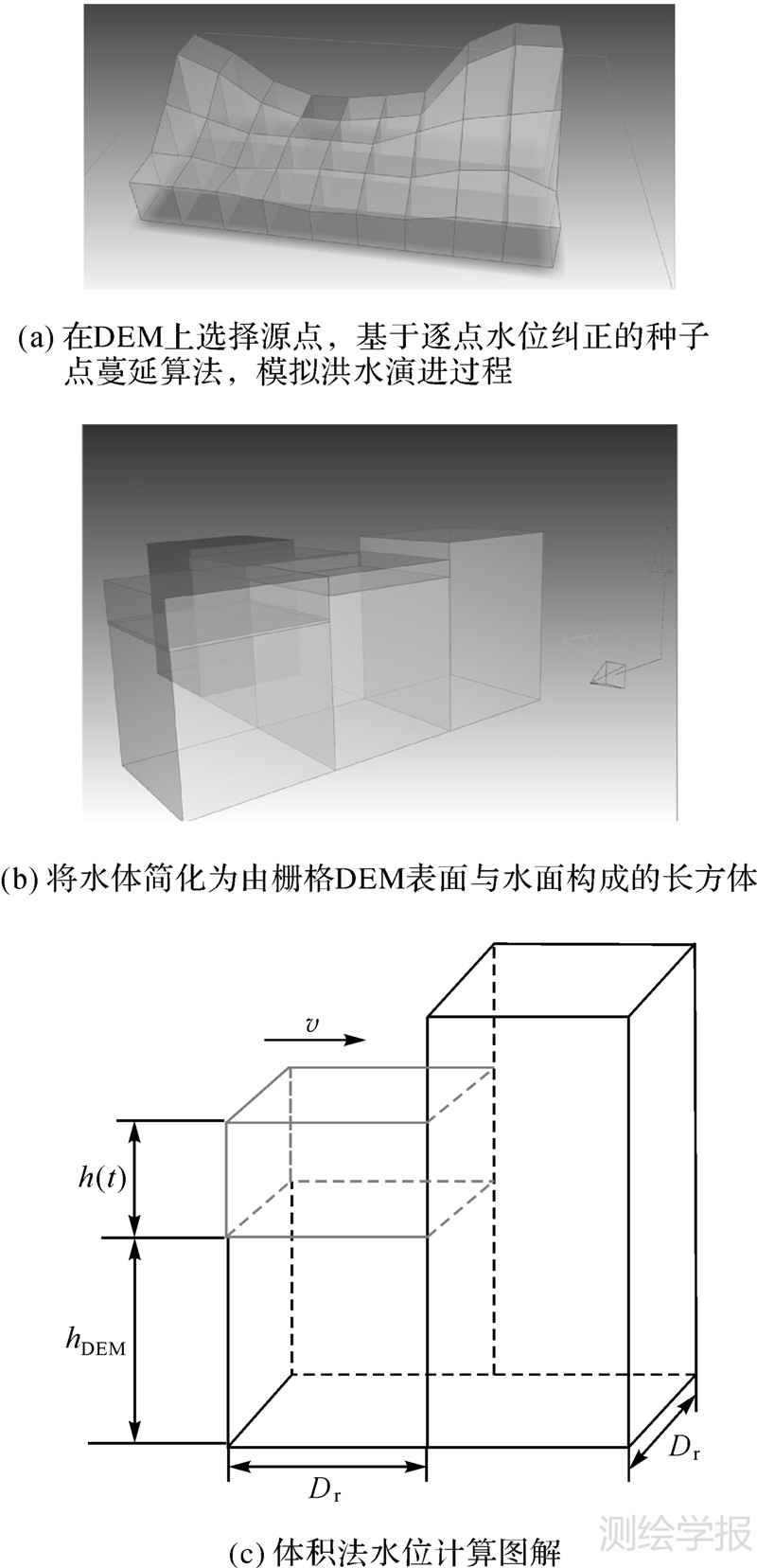
|
| 图 4 逐点水位修正示意图(对每个DEM格网点,选取一个修正邻域,考虑到水流速度和当前水位高度进行水位修正) Fig. 4 Method for water level correction(water level is corrected at each grid in DEM with a specific neighbourhood based on its height and the velocity of flow) |
理论上,洪水水面是一个沿地形起伏的复杂曲面,很难直接求得洪水水面的解析值,为了便于分析,一般需要对水面进行近似和简化。本文采用离散的方法将洪水淹没区离散为与栅格DEM对应的规则格网。对于任意第i行、第j列已被淹没的格网,流入该格网的洪水水量W(i,j)是以该格网水位h(i,j)与高程hDEM之差为高度,以格网当前水位表面为底面的柱体的容积,其中被淹格网的水面面积就简化为该格网在XOY面上投影的矩形面积
式中,W(i,j)标识时段流入该格网洪水水量;Dr为DEM格网间距;h(i,j)为当前格网的洪水水位;hDEM为当前格网的地面高程;i、j为格网行列号。自然地表水流总是由高处向低处流动,又总是沿着坡度最陡的方向流动,高程落差越大的地方,时段内流入的水量就越大。依据这个规律,假定在淹没Δt内流入网格(i,j)内的洪水量和上游来水水位h0与当前格网的水位h(i,j)之差、上游来水流速v以及格网淹没时间Δt成正比,另外考虑到下游流出的水量、流域蒸散发、地表渗透、降雨等对洪水水量的影响,本算法中引入一未知系数μ作为衰减量,可推得经验公式如下
式中,Δt为洪水淹没时间。因此,由式(1)代入式(2)推导可得出,在Δt内,淹没格网内的洪水增长高度为
最后,根据洪水淹没规律,假设在洪水淹没的初始时刻(即淹没时间为0时),格网的水位值同DEM高程hDEM相等(即水深为0);且假设在有限时间Th0内,淹没格网的水位将上涨至源头设置的初始水位h0。则各网格的水位h(t)是以下方程的解
式中,DEM高程hDEM、初始水位h0都是已知量;v为上游来水流速,即在一次洪水过程中某一时段通过漫堤或溃口水流向外流动的速度,流域离散后的不同计算单元流速可以通过水文或水力学[21, 22, 23, 24, 25]方法求解或通过不同水文观测站的流速观测值插值求解。由于式(4)包含两个边界条件,因此可以整理为二次微分方程来求解,令式中λ=μ ,则其解为
,则其解为
为了验证式(4)的可靠性,本文选用某一格网并设定该格网不同的hDEM、初始水位h0、洪水流速v值,进行了相关测试,对不同流速v下某一格网水位随淹没时间变化的状况进行了验证。结果表明,在t∈[0,Th0]内,设定格网的水位是时间的连续函数,并且水位上涨速度在t=0时最快,而在t=Th0时停止上涨。
3 试验与分析 3.1 试验数据本文选用格网间距为5 m的丘陵和复杂山地两种地貌类型的DEM数据进行了试验,如图 5所示。表 1所列为试验数据的基本描述信息,由表中的高程和坡度信息可得出:丘陵低区起伏平缓,绝对高程在0~500 m之间,部分区域地形起伏小,可用于检验水位自阻断流的问题,部分低洼地区可用于验证因洼地导致的水面不连续性问题的处理;复杂山区地形复杂,可用于验证水面爬坡问题的处理。

|
| 图 5 试验数据(图中标注位置为起始淹没点) Fig. 5 Experimental data(source point is pointed out on each area) |
| DEM类型 | 丘陵 | 山地 |
| 最大高程/m | 288.5 | 454.5 |
| 最小高程/m | 79.6 | 33.4 |
| 最大坡度/(°) | 36.3 | 51.5 |
| 最小坡度/(°) | 0.4 | 0.9 |
| 平均坡度/(°) | 14.1 | 35.5 |
| DEM规模 | 19 803×19 902 | 19 803×19 902 |
试验1利用表 1中的试验数据,分别采用传统方法和本文方法进行了对比,对比效果见图 6。图 6(a)所示的洪水淹没区边缘会出现较为明显的水面爬坡现象,而在同一位置下,采用逐点水位修正的洪水淹没分析方法则明显改善了这一问题,水深分布符合自然规律。图 6(c)所示普通种子点蔓延算法在丘陵地形中起伏平缓区域(例如湖面和道路路面等高程起伏较小的区域)会出现明显的水位自阻断流现象,采用逐点水位修正的洪水淹没分析方法则明显地改善了这一问题。

|
| 图 6 淹没效果对比图 Fig. 6 Comparison of flooding analysis results |
试验2,采用表 1中丘陵地区的DEM,进行了2 h的洪水演进模拟。试验结果(图 7)表明,当洪水从源点开始,在DEM起伏较缓的区域进行演进时,淹没范围内没有出现因为地势过于平坦造成水位自阻断流的现象;水面平缓连续,没有出现因为水流在洼地区域的不连续性和在平地区域的不确定和随意性导致水面不连续的问题。分析对比t时刻的历时图和水深分布图(图 8)可得出,淹没区域的水深值是渐变过渡,且淹没范围内任意格网点的水深值与淹没时间对应,淹没时间长的格网点水深值大,淹没时间短格网点水深值小。在洪水蔓延过程中,在已淹没的地形平坦区域,由于引入了自适应逐点水位修正,水位会随淹没时间、流速自适应增长,避免传统水位纠正方法中因全局改正值引起的自阻断流现象。当洪水演进到洼地中时,洼地中的水面会模拟现实水面平缓上升,直至水位高度高于洼地边缘,符合实际洪水蔓延的水流过程。
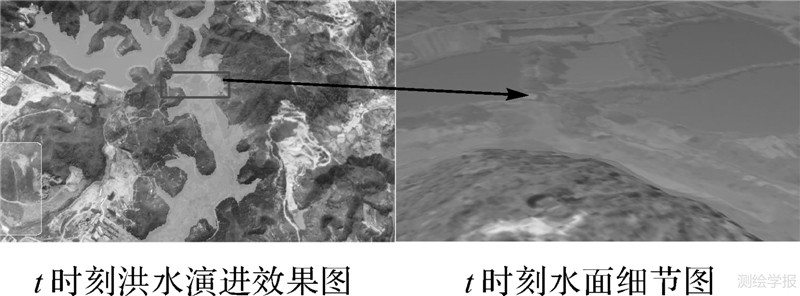
|
| 图 7 丘陵地区淹没效果图 Fig. 7 Flood modeling results in hilly area |
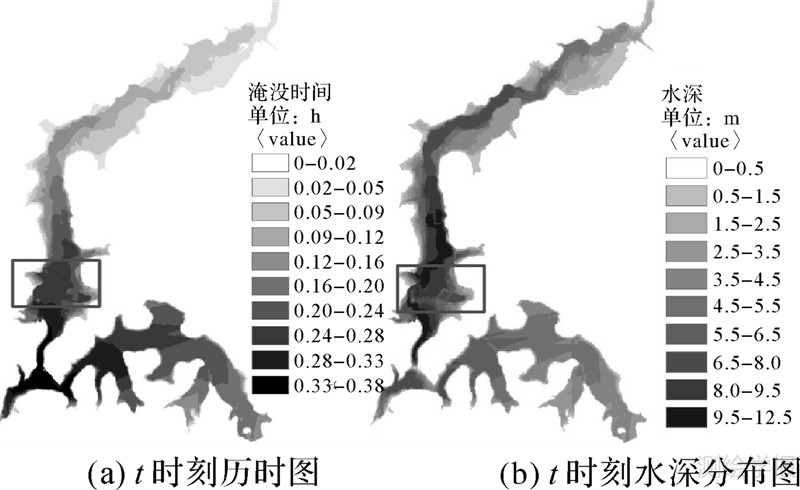
|
| 图 8 丘陵地区淹没历时图和水深分布图 Fig. 8 Flood duration and depth map in hilly area |
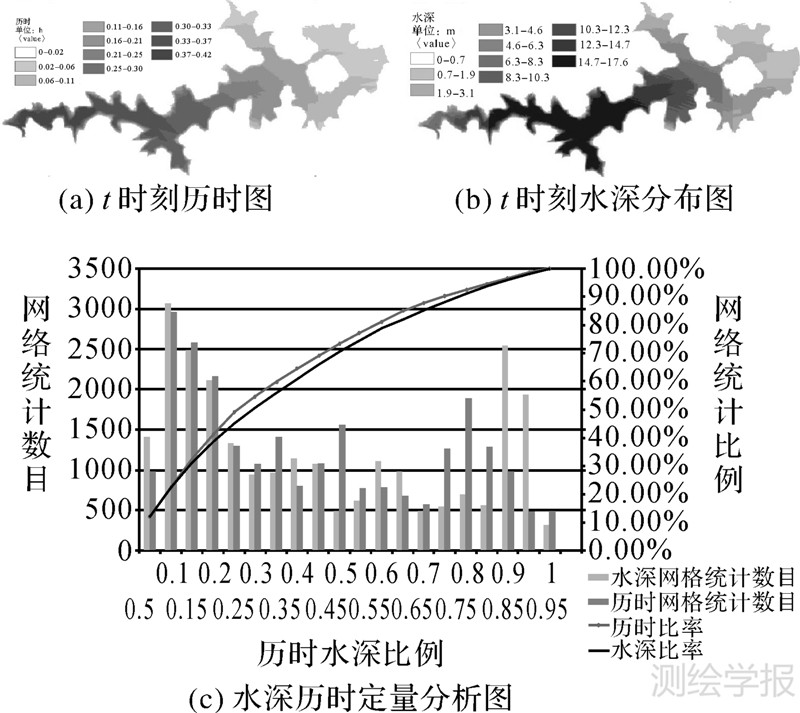
试验3,采用表 1中复杂山区类型的DEM,进行了3 h的洪水演进模拟。试验结果(图 9、图 10)表明,当洪水从起淹点开始,在复杂山区DEM数据上进行演进时,DEM上水深分布是渐变过渡,水面平缓连续,与格网点的淹没时间对应,被淹没的边缘点淹没时间最短,水深最低,接近为0。由于各网格的水深是淹没时间正相关的连续函数,随着淹没时间连续自然增长,水面边缘点水位不会因为陡然加入一个比较大的修正值导致水位突增而出现水面爬坡的现象。

|
| 图 9 复杂山区淹没效果图 Fig. 9 Experimental results in mountain area |
|
| 图 10 复杂山区淹没历时图和水深分布图 Fig. 10 Flood duration and depth map in mountain area |
为了验证水深与淹没时间之间的正相关关系,试验3基于t时刻复杂山区洪水淹没历时图和水深分布图统计获取的水深和历时分段直方图信息,进行了淹没水深和历时之间的定量分析,具体如图 10所示。图 10(c)的横轴“历时水深比例”以0至1代表历时从0至最大历时tmax之间的分布和水深从0到最大水深hmax之间的分布;左纵轴“网格统计数目”代表对应水深或历时下统计的网格数目;右纵轴“网格统计比例”表示网格统计数目与总网格数之比。为了定量分析水深与历时之间的关系,本文从洪水淹没历时图 10(a)上统计获取不同水深值分段区间内对应的网格个数,从水深分布图 10(b)统计获取不同历时值分段区间内对应的网格个数,并将统计的网格数目以直方图的形式显示于图 10(c)中。其中,折线“历时比率”和“水深比率”表示水深和历时不同取值范围内网格数目累加值与总网格数目的比值。由图 10(c)中水深与历时的直方图分布可知,淹没深度和历时基本成正相关关系,只是在分段区间“0.5~0.65”以及“0.75~0.95”之处水深和历时网格统计数目差异较大,这是因为DEM上存在洼地造成的,由2.3节的公式(4)、(5)可知,当洪水演进到洼地区域时,水位差较大,淹没深度会较快速的上涨,导致在较短的淹没时间内达到较大的水深。
4 结 论本文针对洪水演进过程中复杂起伏地形水面爬坡以及平坦地形水位断流的问题,提出了顾及流速和淹没时间的自适应逐点水位修正算法。采用不同地貌类型的DEM数据进行方法验证,试验结果表明:本文方法在种子点蔓延算法的基础上,对各淹没网格的水位进行自适应纠正,有效地解决了传统方法中的水面爬坡、水位断流和水面不连续等问题,提高了洪水淹没范围、水深和洪水历时等模拟结果的可靠性,为洪涝灾害的预警分析和精准评估提供了更加准确的信息。特别的,山地和丘陵地区两个DEM数据文件大小均为1.51 GB,数据量大,洪水演进的动态模拟都能保持每秒35帧以上的速率,证明本文算法是高效实用的。由于洪涝过程复杂,具有动态不确定性特征,已有洪涝灾害模拟模型难以综合考虑复杂环境中的下渗蒸散发、地下径流、地表径流、融雪径流等众多水文过程,导致对洪涝灾害的模拟、评估、预测以及应急响应决策的可靠性不高。因此,为了提高模拟可靠性,进一步的研究将考虑多源来水以及实时观测数据动态接入情况下的水位修正方法,通过实时观测信息与洪涝过程模拟之间的快速/相互检验与修正,达到提高模拟可靠性的目的,从而提升多源传感器信息在突发事件应急响应和环境监测高效分析等方面的分析与应用能力。
| [1] | REGGIANI P, WEERTS A H. A Bayesian Approach to Decision-making under Uncertainty: An Application to Real-time Forecasting in the River Rhine[J]. Journal of Hydrology, 2008, 356(1-2): 56-69. |
| [2] | LIANG Qiuhua. Flood Simulation Using a Well-balanced Shallow Flow Model[J]. Journal of Hydraulic Engineering, 2010, 136(9): 669-675. |
| [3] | BATES P D, DEROO A P J.A Simple Raster-based Model for Flood Inundation Simulation[J]. Journal of Hydrology, 2000, 236(1-2): 54-77. |
| [4] | HASHEMI B L, MOSTAFAVI M A, POULIOT J.3D Dynamic Simulation within GIS in Support of Disaster Management[C]//Lecture Notes in Geoinformation and Cartography.Berlin: Springer Berlin Heidelberg,2007:165-184. |
| [5] | VAN DER KNIJFF J M, YOUNIS J, DE ROO A P J. LISFLOOD: A GIS-based Distributed Model for River Basin Scale Water Balance and Flood Simulation[J]. International Journal of Geographical Information Science, 2010, 24(2): 189-212. |
| [6] | LI Zhiling, ZHU Qing. Digital Elevation Model[M]. Wuhan: Wuhan University Press, 2003. (李志林,朱庆. 数字高程模型[M]. 武汉: 武汉大学出版社, 2003.) |
| [7] | DING Zhixiong, LI Jiren, LI Lin. Method for Flood Submergence Analysis Based on GIS Grid Model[J]. Journal of Hydraulic Engineering, 2004(6): 56-60, 67. (丁志雄, 李纪人, 李琳. 基于GIS格网模型的洪水淹没分析方法[J]. 水利学报, 2004, 67 (6): 56-60.) |
| [8] | LIU Renyi, LIU Nan. A GIS Based Model for Calculating of Flood Area[J]. Acta Geogra Phica Sinica, 2001, 56(1):1-6 (刘仁义, 刘南. 基于GIS的复杂地形洪水淹没区计算方法[J]. 地理学报, 2001, 56(1): 1-6.) |
| [9] | GUO Lihua, LONG Yi. Analysis of Flood Submerging Based on DEM[J]. Bulletin of Surveying and Mapping, 2002(11): 25-27, 30. (郭利华, 龙毅. 基于DEM的洪水淹没分析[J]. 测绘通报, 2002(11): 25-27, 30.) |
| [10] | ZHANG Donghua, LIU Rong, ZHANG Yongxin,et al. The Design and Implement of a New Algorithm to Calculate Source Flood Submerge Area Based on DEM[J]. Journal of East China Institute of Technology (Natural Science), 2009, 32(2): 181-184. (张东华, 刘荣, 张咏新,等. 一种基于DEM的洪水有源淹没算法的设计与实现[J]. 东华理工大学学报:自然科学版, 2009, 32(2): 181-184.) |
| [11] | ZHANG Bingren, QIU Dianming, FENG Yulin. Dynamic Simulation Technology of the Original Flood Evolvement Based on Geo-Process[J]. Journal of Jilin University (Earth Science Edition), 2008, 38(5): 908-912. (张秉仁, 邱殿明, 冯雨林. 面向地学过程的源发型洪水演进仿真技术[J]. 吉林大学学报:地球科学版, 2008,38(5): 908-912.) |
| [12] | ZHU Qing, TIAN Yixiang, ZHANG Yeting. The Extraction of Catchment and Subcatchment from Regular Grid DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 129-133. (朱庆, 田一翔, 张叶廷. 从规则格网DEM自动提取汇水区域及其子区域的方法[J]. 测绘学报, 2005, 34(2): 129-133.) |
| [13] | XU Jingwen, ZHANG Wancang, FU Congbin. A New Method for Treating the Depressions and Flat Areas in DEM for Large-scale Hydrology and Climate Models[J]. Journal of Hydraulic Engineering, 2007, 38(12): 1414-1420. (徐精文, 张万昌, 符淙斌. 适用于大尺度水文气候模式的DEM洼地填充和平坦区处理的新方法[J]. 水利学报,2007, 38(12): 1414-1420.) |
| [14] | XIE Shunping, DOU Jinkang, WANG Lachun. Methods for Processing Depression and Flat Areas in Extracting Drainage Networks Based on the DEM[J]. Advances in Water Science, 2005, 16(4): 535-540. (谢顺平, 都金康, 王腊春. 利用DEM提取流域水系时洼地与平地的处理方法[J]. 水科学进展, 2005, 16(4): 535-540.) |
| [15] | ZHU Qing, ZHAO Jie, ZHONG Zhen, et al. The Extraction of Topographic Patterns Based on Regular Gird DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1):77-82. (朱庆, 赵杰, 钟正, 等. 基于规则格网DEM的地形特征提取算法[J]. 测绘学报, 2004, 33(1): 77-82.) |
| [16] | ZHU Qing, TIAN Yixiang, ZHAO Jie. An Efficient Depression Processing Algorithm for Hydrologic Analysis[J]. Computers and Geosciences, 2006, 32(5): 615-623. |
| [17] | DAVID G. A New Method for the Determination of Flow Directions and Upslope Areas in Grid Digital Elevation Models[J]. Water Resources Research, 1997, 33(2): 309-319. |
| [18] | JENSON S K, DOMINGUE J O. Extracting Topographic Structure from Digital Elevation Data for Geographical System Analysis[J]. Photogrammetric Engineering and Remote Sensing, 1988, 54(11): 1593-1600. |
| [19] | WANG Jianping, REN Liliang, WU Yi. A New Algorithm to Process Depressions in Digital Elevation Model[J]. Geo-information Science, 2005, 7(3): 51-54. (王建平, 任立良, 吴益. 一种新的DEM填洼处理算法[J]. 地球信息科学, 2005, 7(3): 51-54.) |
| [20] | LI Hui, CHEN Xiaoling, ZHANG Lihua. Depression Removal Method for Grid DEM Based on Three-direction Search. Advance in Water Science, 2009, 20(4): 473-479. (李辉, 陈晓玲, 张利华. 基于三方向搜索的DEM中洼地处理方法[J]. 水科学进展, 2009, 20(4): 473-479.) |
| [21] | LI Zhijia, ZHANG Ke, YAO Cheng. Comparison of Distributed Geological Models Based on GIS Technology and DEM[J]. Journal of Hydraulic Engineering, 2006, 37(8): 1022-1028. (李致家, 张珂, 姚成. 基于GIS的DEM和分布式水文模型的应用比较[J]. 水利学报, 2006, 37(8): 1022-1028.) |
| [22] | ZHAO Renjun. Watershed Hydrological Simulation-Xin’anjiang Model and Shanbei Model[M]. Beijing: Water Conservancy and Electric Power Press, 1984. (赵人俊. 流域水文模拟-新安江模型与陕北模型[M]. 北京: 水利电力出版社, 1984.) |
| [23] | WANG Chuanhai, GUO Lijun, RUI Xiaofang. Study on Real-time Flood Forecasting System for the Three Gorges Reservoir[J]. Advance in Water Science, 2003, 14(6): 677-681. (王船海, 郭丽君, 芮孝芳. 三峡区间入库洪水实时预报系统研究[J]. 水科学进展, 2003, 14(6): 677-681.) |
| [24] | ZHANG Ke. Establishment and Analysis of Grid and Topography-based Distributed Xin'anjiang Model[D]. Nanjing: Hohai University,2005. (张珂. 基于DEM栅格和地形的分布式水文模型构建及其应用[D]. 南京: 河海大学, 2005.) |
| [25] | YAO Cheng. Modeling and Analysis of Grid-based Distributed Xin′anjiang Model[D]. Nanjing: Hohai University,2007.(姚成. 基于栅格的分布式新安江模型构建与分析[D]. 南京: 河海大学, 2007.) |
| [26] | CAO Rui.Modeling and Rendering of Floods and Forest Fire Disaster Based on 3D Digital Earth[D].Changsha:National University of Defense Technology,2010.(曹叡.数字地球上的洪水,林火灾害建模与表现[D].长沙:国防科学技术大学,2010.) |