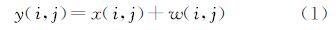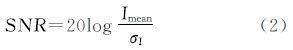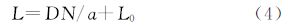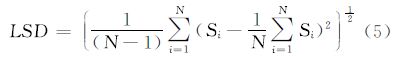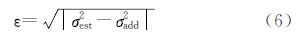1 引 言
遥感卫星成像是对地观测的重要手段之一,随着遥感定量化应用水平不断提高,对遥感器成像质量的要求也越来越高[1]。然而在遥感器成像的过程中,不可避免的受到各种随机因素的干扰,具体表现为各种类型的噪声,引起图像质量下降[2]。通过计算各个子系统的噪声来评估整个遥感成像系统的噪声较难实现,因此可以采用一种简单的数值模型来描述在轨遥感器获取图像的噪声,进而通过对图像中噪声的评估来确定成像系统的噪声水平[3]。
遥感图像中的噪声主要是加性噪声[4],噪声模型可用公式(1)表示
式中,x(i,j)、y(i,j)和w(i,j)分别为坐标(i,j)对应的原始图像信号值、包含噪声的图像值和独立于原始信号x的噪声值,其中图像噪声通常采用零均值的加性高斯白噪声进行模拟。准确地估计遥感图像的噪声水平,可以为后续数据处理算法提供先验参数,还可以对传感器的性能进行检验[5]。在实际应用中,同等水平的噪声对不同信号强度的图像质量影响不同,一般对弱信号图像的影响强于强信号图像,所以估计遥感图像信噪比是十分必要的[6]。同时,信噪比反映了遥感成像系统的辐射性能,是评价成像系统辐射性能的重要指标。文献[7]给出了图像信噪比的不同定义方式和评价方法。特别的,在计算遥感图像的信噪比时,通常采用式(2)进行计算
式中,Imean为图像的灰度均值;σI为噪声标准差,信噪比单位为分贝(db)。近年来,国内外学者对遥感图像的噪声评估进行了深入的研究,提出了多种噪声评估的方法[3, 8, 9, 10, 11, 12, 13, 14, 15, 16]。其中,文献[9]提出的局部标准差法(local standard deviation,LSD)被广泛应用于单波段和多光谱的遥感图像噪声评估。该方法采用对遥感图像进行分块的思想评估图像噪声。局部标准差法计算精度和自动化程度相对较高,对较为均匀的地表区域计算结果较好。但当遥感图像中地物覆盖比较复杂时,图像中存在很多不均匀小图像块,容易导致噪声评估结果出现异常。
目前已有的图像信噪比评估方法中,多数算法将整个图像像素灰度值的均值作为信号的表征,针对遥感图像进行信噪比评估,而忽略了不同遥感图像之间信噪比的比较。在实际应用中,不同卫星遥感器成像系统所获取的图像信噪比的比较、以及相同遥感器不同时期获取的图像信噪比的比较是十分重要的。通过对图像信噪比的比较,可以对比不同遥感器的辐射性能,或者分析同一卫星遥感器在轨运行一段时间后辐射性能的衰退情况。
文献[17]提出了一种可用于不同遥感图像之间信噪比比较的度量准则。该方法通过定义“标准”辐亮度值,将“标准”辐亮度值对应的信噪比进行比较,本文中称之为“标准值比较法”。该准则在一定程度上实现了不同遥感图像之间信噪比的比较,但“标准”辐亮度值的选取对于试验结果有着重要的影响,如何确定“标准”值是一个难点。另一方面,该算法需要在遥感图像中手动选择匀值区域,并要求各个匀值区域具有不同的“亮”、“暗”程度,这在实际操作中较难实现,且不同匀值区域的选择也可能导致最终结果的不同。
针对上述问题,本文提出一种全自动的遥感图像信噪比评估和度量准则,用以评估和比较不同遥感图像的信噪比,并分别采用计算机模拟图像与真实遥感图像进行了试验,同时与标准值比较法进行了对比分析,以验证本文提出的信噪比评估和度量准则的准确可靠性。
2 方 法本文提出的遥感图像信噪比评估和度量准则分为3个主要步骤:遥感图像中匀值图像块的选取、入瞳辐亮度比较范围的确定以及图像信噪比评估和比较,具体流程图如图 1所示。

|
| 图 1 本文算法流程图 Fig. 1 Flow chart of our method |
对于一幅大小为m×n的遥感图像,首先将其划分为若干个小图像块。在遥感图像信噪比的评估算法中,图像的边缘和纹理信息对计算结果的影响较大[1]。分析地物光谱特征可知,同种地物具有相同或相似的光谱特征,在同一波段的遥感图像中就具有相同或相似的灰度值。而图像中的边缘为相邻两种地物的分界线,包含边缘的小图像块可能包含不同的地物,不能用于噪声评估[18]。本文基于边缘提取方法,选取不包含边缘信息的匀值图像块,并以此评估整个图像的信噪比,进一步提升评估结果的准确性。目前存在不少算法能够应用于图像中边缘的提取[19, 20],但精确的提取方法通常计算量较大,而能够快速实现的方法往往需要手动辅助提取或者提取结果精度不够。本文改进了文献[21]算法进行匀值图像块的选取。首先利用一组八方向的二阶滤波窗口对图像进行滤波,滤波算子如图 2所示,滤波窗口大小为3×3。

|
| 图 2 匀值图像块选取滤波窗口 Fig. 2 Data masks for homogeneity detection |
依次使用图 2中的8个滤波窗口对遥感图像进行滤波。对于图像中任一像素点y(i,j)(1≤i≤m,1≤j≤n),假设其原始灰度值为DN(i,j),经过滤波窗口Maskk(1≤k≤8)滤波后对应的像素值为DNk(i,j)。依次经过8个滤波窗口后该点处像素值DNnew(i,j)为各个滤波窗口滤波后数值的绝对值之和,根据式(3)进行计算
如果图像在以像素点y(i,j)为中心的3×3的邻域为平滑区域,则经过图 2中8个方向的滤波窗口滤波之后,理论上该点处的像素值DNnew(i,j)应该为0。然而在真实的遥感图像中,由于噪声的存在,即使该邻域内不存在边缘,DNnew(i,j)一般也不会为0,只是其值相对较小;如果该邻域内存在边缘,经过滤波以后得到的DNnew(i,j)值则相对较大。因此,在得到遥感图像中每个像素点经过了八方向滤波的DNnew值后,通过文献[22]的阈值选取算法确定一个最佳阈值,利用该阈值将全部DNnew值划分为两类。其中DNnew值大于此阈值的像素点被判定为边缘,将该点的像素值设置为255;反之,DNnew值小于或等于此阈值的像素点对应的区域被认为是平滑区域,将该点的像素值设置为0。由此,得到一幅二值图像,白色像素点表示初步提取出的边缘点。
试验中发现,当图像噪声比较严重时,采用上述滤波算法后部分噪声点可能被误认为边缘,这将影响最终试验结果。考虑到噪声往往是独立随机分布,而图像边缘通常是连续的,通过以下假设对二者进行区分:对图像边缘初提取的二值图像进行遍历,对于白色像素点(边缘点),在以该点为中心的3×3的邻域内,若不存在其他白色像素点,则认为该点是噪声;反之确定其为边缘。最终,若划分的图像块内不存在白色像素点,则判定为匀值图像块。对所有的图像块进行遍历,并精确提取出匀值图像块。
2.2 入瞳辐亮度区间范围选择自然界中不同类型的地物由于化学组分、物质结构的差异,具有反射或辐射不同波长电磁波的特性[23]。遥感成像系统的成像过程实际上是景物反射的太阳辐射和自身辐射的电磁波经过大气和光学系统作用后到达传感器并被接受。对不同遥感图像进行信噪比的比较需要将图像上像素点的灰度值转换为遥感器成像时的入瞳辐亮度,对应到相同入瞳辐亮度的条件下才能进行比较,其结果才能反映出遥感器辐射性能的好坏。通过辐射定标系数可以将图像灰度值DN转换为入瞳辐亮度L。L的单位为W·m-2·sr-1·μm-1,L可以通过式(4)进行计算
式中,a为绝对定标系数增益;L0为偏移量。这两个参数都需要通过绝对辐射定标得到,其值可以从遥感数据的头文件中获取。
对于待比较的遥感图像,按照1.1节的方法选取出匀值图像块,计算每个匀值图像块的平均灰度值DN,并采用式(4)将每个匀值图像块的DN值转换为入瞳辐亮度L。分别找出两幅待比较遥感图像中匀值图像块对应辐亮度的最小值Lmin,α和最大值Lmax,α,其中α=1,2,用以区分待比较的两幅输入图像。将两幅遥感图像匀值图像块的辐亮度统一到相同的区间范围,即用来进行信噪比比较的辐亮度区间为
需要指出的是,采用本文提出的信噪比度量准则对不同遥感图像的信噪比进行比较时,需要两幅待比较图像中匀值图像块的辐亮度区间存在重叠部分,否则算法无法进行有效的比较。幸运的是,在实际中大多数情况能满足此要求。
2.3 信噪比评估和比较将辐亮度区间等间隔划分为P个小区间,本文中所有试验统一设定P=20。对于待比较的两幅遥感图像,统计对应的辐亮度值落在每个小区间的匀值图像块。将每个辐亮度小区间对应的匀值图像块分别采用式(5)计算噪声的局部标准差(LSD)
式中,Si表示图像块中第i个像素的灰度值;N为当前图像块的像素总数。利用局部标准差法计算每个辐亮度小区间对应图像块的噪声标准差,并将该辐亮度区间对应所有图像块的灰度平均值与噪声标准差之比作为该区间对应图像块的信噪比。由此可以得到在相同的辐亮度范围下两幅遥感图像的信噪比曲线,从而进行不同遥感图像之间信噪比的比较。 3 试验与分析 3.1 试验1:验证匀值区域选择的准确性与稳定性为了验证滤波算子选取匀值图像块方法的准确性,以及基于匀值图像块的局部标准差方法评估噪声的准确性和稳定性,通过计算机仿真的模拟图像进行试验。图 3(a)显示了一幅采用3D-MAX软件仿真得到的自然地物模拟图像,包括山脉、湖面、田野以及一些人工地物,图像中不包含噪声。在图 3(a)所示图像中加入标准差为6的高斯白噪声,得到包含噪声的图像,如图 3(b)所示。采用4×4大小的分块将图 3(b)分为若干图像块,如图 3(c)所示。首先利用八方向滤波算子对加噪后图像进行了边缘的初步提取,结果如图 3(d)所示。通过1.1节中区分噪声和边缘的假设,更为精确地提取到图像边缘信息,基本排除了噪声的干扰,结果如图 3(e)所示。最终选取的匀值图像块如图 3(f)所示,其中黑色的图像块为匀值图像块。

|
| 图 3 利用模拟图像进行匀值图像块选取试验 Fig. 3 Experiments of homogeneity detection with simulation images |
需要指出的是,图像中噪声的大小对匀值图像块的选取有一定的影响,对于加入不同水平噪声的图像进行试验的结果表明:当噪声标准差不超过10时,采用本文方法进行匀值图像块选取效果较好;而当噪声标准差大于10以后,部分噪声仍会被误认为是图像边缘,导致匀值图像块的选取有误。而在真实遥感图像中噪声的标准差一般较小,因此采用本文方法进行匀值图像块的选取是可行的。
本文方法通过对提取的匀值图像块采用局部标准差法进行噪声评估,为了验证该方法的准确性和稳定性,在图 3(a)中加入均值为0,标准差分别为1、2、3、…、8的高斯白噪声,并通过噪声评估误差ε进行量化比较,如公式(6)所示
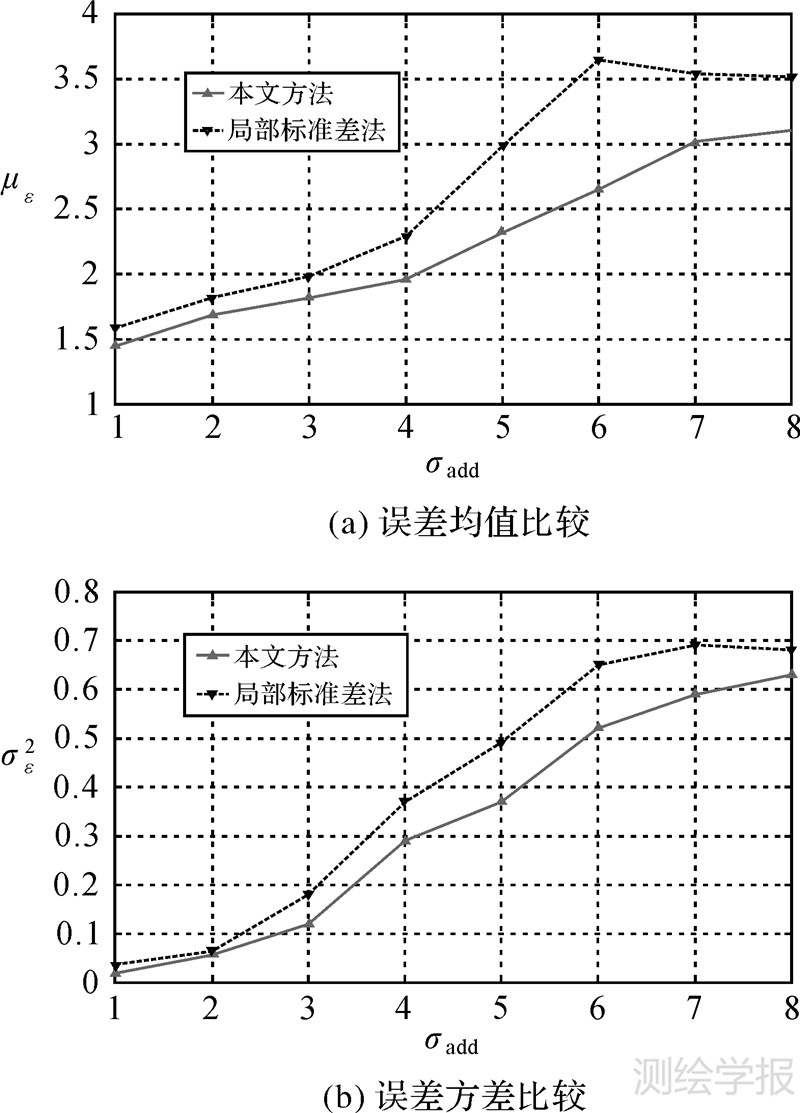
式中,σest为采用某种算法对图像进行评估得出的噪声标准差;σadd为在无噪声的理想图像中加入的噪声标准差。为了确保试验结论的可靠性,对每一幅图像进行了50次重复试验,并计算噪声评估误差的均值με和方差σε2。对图 3(a)中的模拟图像加入不同程度的噪声后,采用匀值块选取-局部标准差法与直接采用局部标准差法进行图像噪声评估结果的比较如图 4所示。
|
| 图 4 本文方法与局部标准差法进行图像噪声评估的误差均值比较和误差方差比较 Fig. 4 Comparison of με and σε2 between the proposed algorithm and LSD |
从图 4中可以看出,在理想图像中加入噪声标准差为1~8的高斯白噪声时,采用本文方法测得的噪声值要比直接采用局部标准差法计算得到的结果更加准确。在重复进行的50次试验中,采用本文方法计算得到的噪声值更加稳定,可靠性更高。由此可见,本文中采用的先匀值块选取再计算局部标准差的方法是可行的。
3.2 试验2:比较相同遥感器不同时期图像信噪比本节选用环境与灾害监测预报小卫星星座A星(HJ-1A星)的遥感图像进行试验。HJ-1A星搭载了两台CCD相机和超光谱成像仪,试验中通过对不同时期CCD1相机图像的信噪比进行评估和比较,分析CCD1相机性能衰退的情况,CCD1相机的主要参数如表 1所示。
| 平台 | HJ-1A星 | |||
| 有效载荷 | CCD1相机 | |||
| 波段号 | 1 | 2 | 3 | 4 |
| 光谱范围/μm | 0.43 0.52 | 0.52 0.60 | 0.63 0.69 | 0.76 0.90 |
| 空间分辨率/m | 30 | 30 | 30 | 30 |
| 重访时间/d | 4 | |||
试验中采用了不同时期CCD1相机遥感图像作为试验图像,其图像包含了4个波段,为了方便显示,图 5(a)、(b)中的原图为第1波段图像,成像地点均为甘肃省敦煌市,其中图 5(a)成像时间是2009-09-27,图 5(b)成像时间是2011-07-15,两幅图像成像时间相隔将近两年。利用本文的方法对不同遥感图像信噪比进行评估和比较,需要根据公式(4)将遥感图像的DN值与成像时传感器入瞳辐亮度进行转换,这就要获取试验中每幅遥感图像对应的辐射定标系数。HJ-1A星在轨运行之后,我国每年都要在敦煌辐射校正场、青海湖辐射校正场开展定标及真实性检验试验,成功获取了所需试验数据,表 2所示为试验中遥感图像对应的辐射定标系数。

|
| 图 5 HJ-1A星CCD1相机试验图像 Fig. 5 Experimental images of CCD1 camera in HJ-1A satellite |
| 图像编号 | 波段号 | a | L0 |
| 图 5(a) | 1 | 0.576 3 | 9.318 3 |
| 2 | 0.541 0 | 9.175 8 | |
| 3 | 0.682 4 | 7.507 2 | |
| 4 | 0.720 9 | 4.148 4 | |
| 图 5(b) | 1 | 0.776 8 | 7.325 0 |
| 2 | 0.779 6 | 6.073 7 | |
| 3 | 1.031 2 | 3.612 3 | |
| 4 | 1.004 9 | 1.902 8 |
采用本文提出的信噪比评估和度量准则对这一组图像进行试验,试验结果如图 6所示,其中图 6(a)~(d)分别对应第1波段至第4波段图像的试验结果。

|
| 图 6 2009、2011HJ-1A星辐亮度-信噪比曲线 Fig. 6 Apparent radiance-SNR curve for images of HJ-1A satellite in 2009 and 2011 |
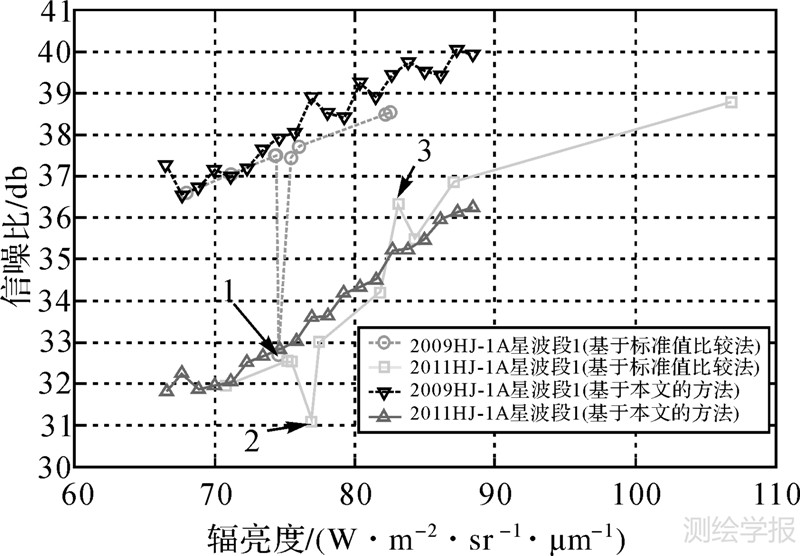
同时,采用标准值比较法[17]对该组遥感图像的第1波段图像进行了信噪比的评估和度量比较。首先分别在每幅图像中手动选取了10个“匀值”图像块,图像块大小为200像素×200像素,选取的结果在图 5(a)、(b)中标明。比较试验结果如图 7所示。
|
| 图 7 本文方法与标准值比较法比较结果 Fig. 7 Comparison of the results between the proposed method and normalized-value based method |
根据图 7可以看出,采用标准值比较法得到的试验结果中出现了几个非常明显的异常点:如对图 5(a)进行试验得到结果曲线中的点1,以及图 5(b)对应的试验结果中的点2和点3。以点1为例,该点对应于图 5(a)中手动选取的匀值图像块7,由于边缘信息的影响,采用局部标准差法进行图像噪声评估所得的结果较大,信噪比较小。出现异常值的点2和点3同样如此。本身在地物复杂的遥感图像中手动选择匀值图像块就很困难,图像块灰度值的均匀性很难得到保证。此外,匀值图像块的尺寸一般较小,采用局部标准差法进行信噪比评估时出现异常值的情况难以避免,而一定数量异常值的出现会严重影响最终试验结果。相比较而言,由于本文算法采用匀值图像块的自动选取,且将辐亮度区间等间距划分进行信噪比的度量比较,故试验结果曲线较为平稳,没有异常值的出现。
此外,由图 7可以看出,通过标准值比较法手动选取匀值图像块进行试验,由于两幅图像对应的入瞳辐亮度区间范围差别较大(图 5(a)对应的辐亮度范围是68~82.5,图 5(b)对应的辐亮度范围是71~107),使得“标准”辐亮度值的选取至关重要。针对不同的试验图像,该方法需要设定不同的“标准”辐亮度值,试验操作难度较大,限制了算法的实用性。本文方法通过选取两幅待比较图像辐亮度的重叠部分,直接在重叠的辐亮度区间进行比较,避免了“标准”辐亮度值的手动选取对于估计结果的影响以及异常点的出现。
3.3 试验3: 比较不同遥感器成像系统图像信噪比利用本文提出的遥感图像信噪比评估和度量准则,对HJ-1A星CCD1相机与CBERS-02B星(中巴资源卫星2号,简称02B星)CCD相机分别在轨运行一年后所获取的遥感图像的信噪比进行了评估和比较。02B星于2007年9月19日在中国太原卫星中心发射成功,星上搭载的CCD相机的主要参数如表 3所示。
| 平台 | 02B星 | ||||
| 有效载荷 | CCD相机 | ||||
| 波段号 | 1 | 2 | 3 | 4 | 5 |
| 光谱范围/μm | 0.45 0.52 | 0.52 0.59 | 0.63 0.69 | 0.77 0.89 | 0.51 0.73 |
| 空间分辨率/m | 20 | 20 | 20 | 20 | 20 |
| 重访时间/d | 26 | ||||
根据表 3可知,02B星CCD相机具有5个波段,前4个波段与表 1中HJ-1A星CCD1相机的波段范围基本一致,第5个波段为全色光波段,试验中将02B星CCD相机的前4个波段与HJ-1A星CCD1相机的波段1至波段4对应图像的信噪比分别进行评估和比较。试验3中采用的HJ-1A星的图像如图 5(a)所示,02B星的图像如图 8所示,图中所示为第1波段图像,成像地点为敦煌地区,成像时间为2008-09-03。

|
| 图 8 2008年敦煌地区02B星CCD相机波段1图像 Fig. 8 02B CCD image band 1 at Dunhuang in 2008 |
同样,02B星在轨运行之后,中国资源卫星应用中心定期组织开展敦煌绝对辐射校正场的外场定标试验,试验2中采用的02B星图像的辐射定标系数如表 4所示,其中第5波段的定标系数未予列出。
| 图像编号 | 波段号 | a | L0 |
| 图 8 | 1 | 1.072 5 | 0 |
| 2 | 0.909 8 | 0 | |
| 3 | 1.517 0 | 0 | |
| 4 | 1.757 7 | 0 |
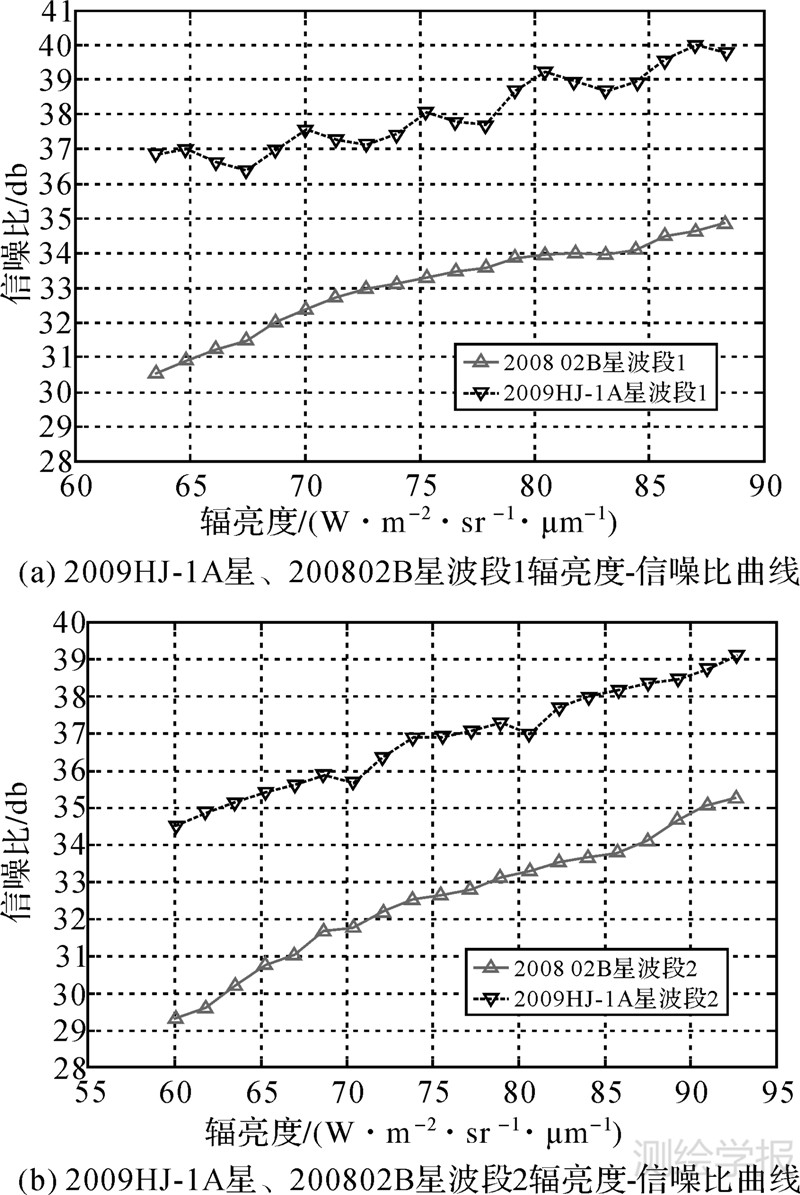
根据本文提出的遥感图像信噪比评估和度量准则,分别对图 5(a)和图 8对应的各个波段的试验图像信噪比进行评估和比较,试验结果如图 9所示。
|
| 图 9 2009HJ-1A星、200802B星图像辐亮度-信噪比曲线 Fig. 9 Apparent radiance-SNR curve for images of HJ-1A satellite in 2009 and images of 02B satellite in 2008 |
由图 9(a)~(d)可知,同样在轨运行一年以后,两颗卫星4个波段图像的信噪比差异基本一致:HJ-1A星CCD1相机图像的信噪比要比02B星CCD相机图像的信噪比高出约4~6 dB,即在轨运行一年后HJ-1A星CCD1相机的性能要略好于02B星CCD相机。
4 结 论通过遥感图像匀值图像块的自动选取以及图像灰度值与入瞳辐亮度值的相互转换,本文提出了一种遥感图像信噪比的评估和比较方法,并以该方法作为两幅遥感图像信噪比比较的度量准则。试验结果验证了本文方法较之于其他同类方法具有更高的稳定性和可靠性。需要指出的是,采用本文方法比较不同遥感图像的信噪比,两幅待比较图像中匀值图像块对应的辐亮度区间必须存在重叠部分。另一方面,本文方法采用加性噪声模型进行信噪比评估,如何估计以乘性噪声为主的遥感图像信噪比将是未来工作的重点。
| [1] | WANG Xiaotian, SHI Guangming, NIU Yi. Translation Invariant Omni Directional Lifting Based Remote Sensing Image Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 555-562. (王晓甜,石光明,牛毅. 基于移不变全方向角提升的遥感图像降噪[J]. 测绘学报, 2011, 40(5): 555-562.) |
| [2] | WANG Xianghai, ZHANG Hongwei, LI Fang. A PDE-based Hybrid Model for De-noising Remote Sensing Image with Gaussian and Salt-pepper Noise[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 283-294. (王相海,张洪为,李放. 遥感图像高斯与椒盐噪声的PDE混合去噪模型研究[J]. 测绘学报, 2010, 39(3): 283-294.) |
| [3] | GAO Lianru, ZHANG Bin, ZHANG Xia, et al. Study on the Method for Estimating the Noise in Remote Sensing Images Based on Local Standard Deviations[J]. Journal of Remote Sensing, 2007, 11(2): 203-208. (高连如, 张兵, 张霞, 等. 基于局部标准差的遥感图像噪声评估方法研究[J]. 遥感学报, 2007, 11(2): 203-208.) |
| [4] | CORNER B R, NARAYANAN R M, REICHENBACH S E. Noise Estimation in Remote Sensing Imagery Using Data Masking[J]. International Journal of Remote Sensing, 2003, 24(4): 689-702. |
| [5] | CHEN Zhengchao. A Research on the Technology of On-orbit Calibration and Validation of China DMC Microsatellite[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2000. (陈正超. 中国DMC小卫星在轨测试技术研究[D]. 北京:中国科学院研究生院, 2000.) |
| [6] | CHEN Qiulin, XUE Yongqi. Estimation of Signal-Noise-Ratio from Data Acquired with OMIS[J]. Journal of Remote Sensing, 2000, 4(4): 284-289. (陈秋林,薛永祺. OMIS成像光谱数据信噪比的估算[J].遥感学报, 2000, 4(4): 284-289.) |
| [7] | FIETE R D, TANTALO T. Comparison of SNR Image Quality Metrics for Remote Sensing Systems[J]. Optical Engineering, 2001, 40(4): 574-585. |
| [8] | MEER P, JOLION J M, ROSENFELD A. A Fast Parallel Algorithm for Blind Estimation of Noise Variance[J]. IEEE Transactions on Pattern Analysis and Machine Intel-ligence, 1990, 12(2): 216-223. |
| [9] | GAO B C. An Operational Method for Estimating Signal to Noise Ratios from Data Acquired with Imaging Spectrometers[J]. Remote Sensing of Environment, 1993, 43(1): 23-33. |
| [10] | ROGER R E, ARNOLD J F. Reliably Estimating the Noise in AVIRIS Hyperspectral Images[J]. International Journal of Remote Sensing, 1996, 17(10): 1951-1962. |
| [11] | LIU C, WILLIAM T, SZELISKI R, et al. Noise Estimation from a Single Image[R]. Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington DC: IEEE Computer Society, 2006: 901-908. |
| [12] | MOGHADDAM M E, JAMZAD M. Linear Motion Blur Parameter Estimation in Noisy Images Using Fuzzy Sets and Power Spectrum[J]. EURASIP Journal on Advances in Signal Processing, 2007, 207: 1-8. |
| [13] | GAO L R, ZHANG B, ZHANG X, et al. A New Operational Method for Estimating Noise in Hyperspectral Images[J]. IEEE International Geoscience and Remote Sensing Letters, 2008, 5(1):83-87. td> |
| [14] | SANTIAGO A F, GONZALO V S F, MARCOS M F, et al. Automatic Noise Estimation in Images Using Local Statistics: Additive and Multiplicative Cases[J]. Image and Vision Computing. 2009, 27: 756-770. |
| [15] | LOQUIN K, STRAUSS O. Noise Quantization via Possi bilistic Filtering[C]//Proceedings of 6th International Symposium on Imprecise Probability: Theories and Applica tions. Durham:Durham University, 2009. |
| [16] | NAIR M S, RAJU G. Additive Noise Removal Using a Novel Fuzzy-based Filter[J]. Computers and Electrical Engineering, 2011, 37(5): 644-655. |
| [17] | WANG X H, TANG L L, LI C R, et al. A Practical SNR Estimation Scheme for Remotely Sensed Optical Imagery[C]//Proceedings of the SPIE: 73848: International Symposium on Photoelectronic Detection and Imaging 2009: Advances in Imaging Detectors and Applications. Beijing: SPIE, 2009: 1-6. |
| [18] | ZHU Bo, WANG Xinhong, TANG Llinli, et al. Review on Methods for SNR Estimation of Optical Remote Sensing Imagery[J]. Remote Sensing Technology and Application, 2010, 25(2): 303-309. (朱博,王新鸿,唐伶俐, 等. 光学遥感图像信噪比评估方法研究进展[J]. 遥感技术与应用, 2010, 25(2): 303-309.) |
| [19] | CANNY J. A Computational Approach to Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679-698. |
| [20] | ZHENG S, LIU J, TIAN J W. A New Efficient SVM-based Edge Detection Method[J]. Pattern Recognition Letters, 2004, 25(10): 1143-1154. |
| [21] | AMER A, DUBOIS E. Fast and Reliable Structure-oriented Video Noise Estimation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2005,15(1): 1-6. |
| [22] | OTSU N. A Threshold Selection Method from Gray-level Histograms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1975, 9(1): 62. |
| [23] | YU Junna. Research on the Hyperspectral Imagery Classi-fication Based on the Neural Network[D]. Harbin: Harbin Engineering University, 2007. (于君娜. 基于神经网络的高光谱遥感图像分类研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.) |