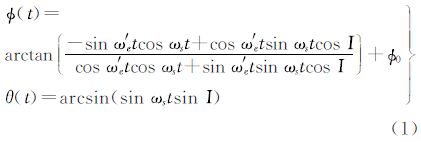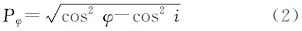2. 65015部队,辽宁 大连 116023
2. 65015 Troops,Dalian 116023,China
1 引 言
全球气候环境对全球和局部海域海平面变化具有重大影响,利用卫星测高数据监测海平面变化是重要的海洋科学研究手段之一。其中最具代表性的有T/P系列卫星,其主要任务就是对全球海平面及洋流进行监测[1, 2, 3]。在过去近20年中,T/P(1992)、Jason-1(2002)以及Jason-2(2008)测高卫星对全球海洋进行不间断观测,积累了大量海洋科学数据。利用这些数据,国内外诸多学者对全球或区域海平面变化情况进行了深入研究。文献[4]利用T/P、ERS-1及验潮站数据得到全球海平面平均上升速率约为2.2 mm/a;文献[5]联合T/P、ERS-1及ERS-2数据得出速率约为3.3 mm/a;文献[6, 7, 8]分别讨论了T/P与Jason-1、Jason-2卫星数据联合处理问题,并得到连续海平面变化时间序列;文献[9, 10]利用卫星测高和验潮站数据分别研究了阿拉伯海域和欧洲南部海域的海平面变化情况;文献[11, 12]分别探讨了Jason-2与Jason-1卫星数据的连续性问题,并各自联合3颗卫星数据建立了最新全球海平面变化时间序列,从1993-2009年,全球海平面平均上升速率约为3.3 mm/a;文献[13]利用T/P数据研究了全球海平面的变化情况;文献[14, 15]分别利用CPCA和小波分析方法基于T/P数据研究了我国海平面变化的频域特征;文献[16, 17]利用T/P和Jason-1数据对中国近海海平面变化做了初步研究;文献[18, 19]联合Geosat、ERS-1、ERS-2、Envisat、T/P和Jason-1数据构建了全球平均海面高模型。这些研究的进行,为我国海域和世界范围的海平面变化研究提供了重要参考依据。
Jason-2卫星发射升空已经3年有余,期间积累的大量高精度观测数据对研究海平面变化具有重要意义。目前全球性海平面变化研究已经全面展开,但是针对我国海域的研究成果还较少,且针对我国海域的Jason-2卫星数据应用研究的相关文献论述较少。研究表明,T/P系列卫星虽然采用相同的设计轨道,但各卫星观测数据之间存在较大的系统差。文献[11]得出的结论适用于全球范围的研究,但在不同的区域,各卫星之间的系统差不同,国内对此进行专门研究的相关文献论述较为少见。本文以对在我国海域附近各卫星之间系统差的深入分析为基础,联合T/P、Jason-1和最新的Jason-2卫星数据,从而建立我国各海域较大时间跨度范围的卫星测高海平面变化时间序列,对我国近海及邻域20年变化情况进行分析研究。
2 海面高计算本文采用的卫星测高数据是由法国AVISO数据中心发布的新一代卫星测高数据产品,该数据利用geophysical data record(GDR)数据重新处理得到,已经剔除了覆盖陆地、冰面等地区的无效数据。GDR数据的详细编辑标准参见文献[20]。值得注意的是,该数据在处理地球物理环境偏差改正时,对3颗卫星采用相同改正模型重新计算改正值,有效保证了数据的连续性;使用重新计算的精密轨道数据,有效提高了海面高观测精度。表 1列出了文中所使用的数据周期及时间跨度情况。
| 卫 星 | 周 期 | 时 间 |
| T/P | Cycle 11~363 | 1993-01-2002-08 |
| Jason-1 | Cycle 1~259 | 2002-02-2009-01 |
| Jason-2 | Cycle 1~117 | 2008-07-2011-09 |
测高卫星的正常点是指卫星在预先设计的冻结轨道上运行时不同周期精确重复观测的星下点。T/P、Jason-1和Jason-2卫星正常点轨迹理论上是相同的,而实际上不同周期的观测点位置会存在1~2 km的偏差。为了能够对不同周期的数据作统一处理,需要计算每条弧段所对应的正常点轨迹,进而将不同周期相同弧段的观测值内插到相同观测轨迹上。在升交点经度已知的条件下,正常点的计算公式为[21]
式中,Φ(t)、θ(t)分别表示距升交点t时刻正常点位置的经纬度;Φ0表示升交点经度;ω′e=ωe-ωn,ωe表示地球自转角速度,ωn表示升交点赤经变化率,ωs表示卫星自转角速度;I表示卫星轨道倾角。利用式(1)可计算出t时刻升弧段正常点位置的经纬度;降弧段的计算方法与其类似,先将其按照升弧段方法计算,然后进行逆向排序即可。 2.2 正常点海面高正常点海面高的计算,就是利用插值算法,将各周期同一弧段实测的沿轨迹离散数据内插到上述计算出的正常点轨迹上,形成不同周期相同点位的观测数据。本文采用不等距三次样条插值算法[22],该算法具有较好的稳定性,且考虑了插值邻域边界处的海面高梯度,能够有效保证各插值点之间的连续性。具体方法是:对于一条轨迹上的某个正常点,以该点为中心、以15′为窗口大小搜索观测值,以搜索到的观测值采用不等距三次样条插值算法计算该正常点的海面高;若搜索到的观测值少于3个,则认为卫星在该点的观测质量较低并舍弃该正常点的海面高内插值。
利用上述算法,本文对该区域内3颗卫星共730个周期各42条弧段观测数据进行插值计算,得到各周期沿正常点轨迹分布的1 Hz采样率的海面高数据。
2.3 粗差剔除利用三次样条函数插值计算正常点海面高,能够一定程度上剔除陆地附近数据的影响;在近海,虽然测高回波所受影响远小于陆地附近,但是其数据质量仍然受到了较大污染,需要采取一定的方法剔除。根据文献[23]中对海面高梯度数据的处理方法,将其引入到海面高数据的处理。基本思想是:认为某一弧段上的所有正常点海面高数据是一个以与升交点的距离为独立变量的时间序列。将该时间序列输入高斯滤波器[24, 25],滤波后的结果与原始数据作比较并计算标准偏差,找出偏差绝对值最大的点,若大于3倍标准偏差,则认为该点是粗差并将其剔除,然后再次对剔除粗差后的数据进行滤波,重复以上步骤,直到最大偏差小于3倍标准偏差为止。
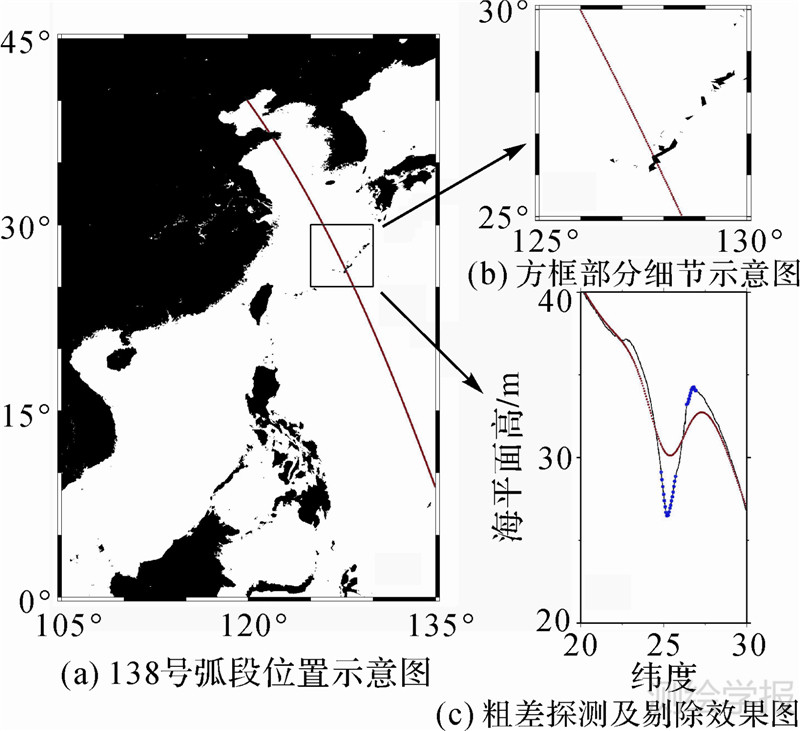
下面以T/P卫星138号弧段Cycle180周期数据为例说明该方法对于探测并剔除近海数据效果。图 1(a)是138号弧段的位置示意图,图 1(b)是图 1(a)中方框部分即纬度25°~30°、经度125°~130°之间的细节示意图,其中黑色区域为陆地和海岛;图 1(c)是粗差探测的效果,滤波半径取为8 km[23],其中黑色线条是原始观测值,红色线条是迭代应用高斯滤波之后的结果,而蓝色圆点则是被剔除的原始数据中的粗差。与图 1(b)比较可以发现,剔除的粗差正是被认为是粗差的卫星在海岛附近的观测值,这些粗差的偏差量级均在米级以上,若不加以剔除,将对最终结果造成较大影响。由图 1(c)的结果可以看出,该方法在剔除海面高粗差方面是行之有效的。
|
| 图 1 T/P卫星138号弧段位置及其数据粗差剔除结果 Fig. 1 Position of T/P satellite 138 arc segment and the result of rejected outliers |
经过上述两个步骤的处理,3颗卫星位于该区域的共730个周期各42条弧段观测数据最终剔除的数据量列于表 2。
| 数据量 | 占总数据量百分比/(%) | |
| 附近少于3个观测值 | 92 167 | 0.17 |
| 粗差 | 889 141 | 1.64 |
| 剔除数据总数 | 982 308 | 1.81 |
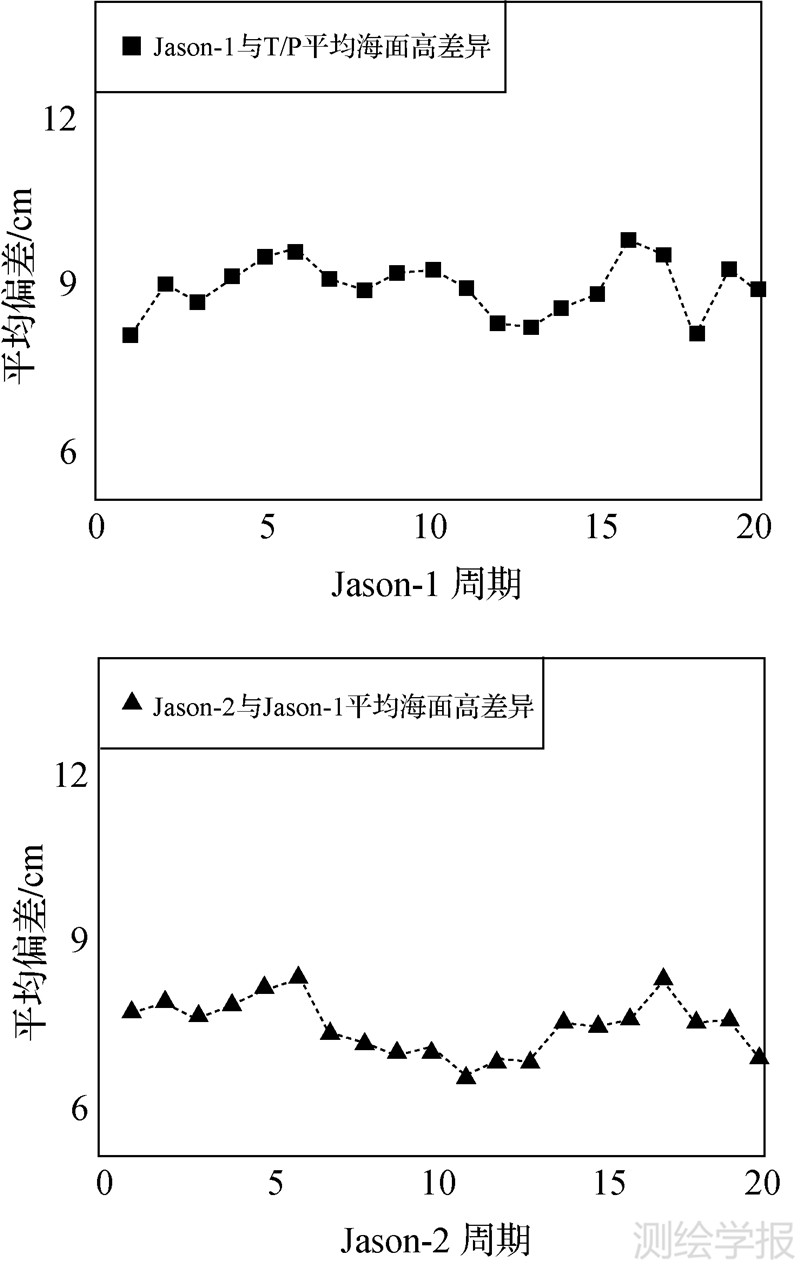
为了检验和校正新发射卫星观测数据的质量,Jason-1发射后,与T/P卫星间隔一定距离成共线轨道飞行,同样,Jason-2也与Jason-1保持一定距离共线飞行,时间间隔约为1 min[3]。然后,新发射的卫星轨道不变,另一颗卫星实施轨道机动,与新卫星形成观测星座,提高数据在全球范围内的分辨率。两次共线飞行对应的周期分别是:T/P Cycle 344~363对应Jason-1 Cycle 1~20;Jason-1 Cycle 240~259对应Jason-2 Cycle 1~20。利用编队飞行的观测数据,可以对3颗卫星联合处理时存在的偏差进行分析和校正。
数据分析与研究表明,尽管T/P、Jason-1和Jason-2卫星在近乎相同的轨道上运行,地面轨迹重合,但是在全球范围内,Jason-1卫星的观测值超出T/P约15 cm,而Jason-2卫星的观测值超出Jason-1约8 cm[6, 11]。在进行海平面变化研究时,通常的数据处理做法是:以T/P观测数据为参考,对Jason-1和Jason-2的观测数据分别施加常数改正,从而有效保证3颗卫星数据的连续性。而文献[6, 11]在全球范围内得出的改正常数用于中国近海等局部海域可能会造成较大误差,因此,应首先确定3颗卫星在中国附近海域(105°E~135°E,0°N~45°N)的平均偏差。
利用沿轨迹正常点海面高观测值,分别计算两次共线任务观测数据的平均偏差,计算方法是:对每周期的观测数据取空间平均,得到该周期对应的平均海面高,然后将对应周期的平均海面高作差,得到其对应的平均偏差。两次共线任务各同步周期对应的平均偏差结果如图 2所示。
|
| 图 2 两组编队飞行所得海面高数据平均差异 Fig. 2 Mean bias of SSH during formation flight phase |
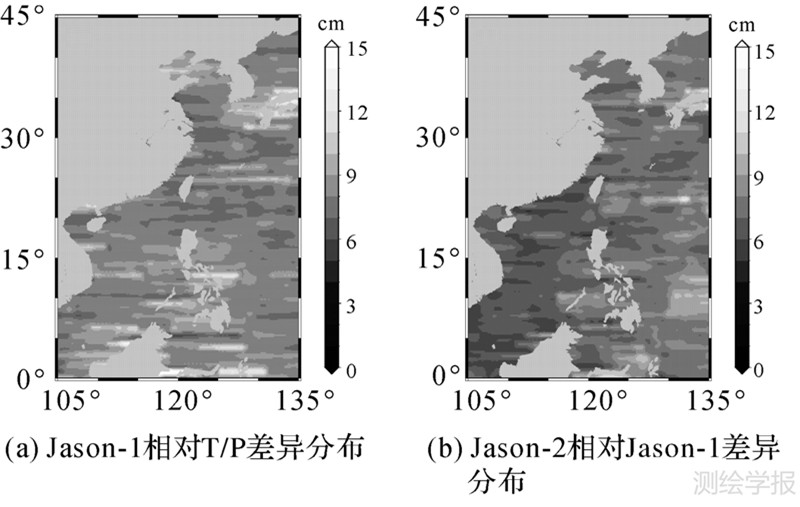
再对20个周期数据取时间平均并利用3倍中误差的方法进一步剔除粗差,得到3颗卫星正常点平均海平面高,并分别将其格网化。格网化方法在文献[19]中已有详细分析,不再赘述。本文采用Shepard格网化方法[19, 26]。分别对编队飞行期间的格网平均海面高进行比较,所得比对结果如图 3所示。
|
| 图 3 海面高差异分布 Fig. 3 SSH differences during formation flight phase |
分别统计对各海域的平均偏差,各海域概略范围分别是:渤海(117.5°E~122°E,37°N~41°N);黄海(119°E~126°E,33°N~37°N);东海(120°E~127°E,23°N~33°N);南海(110°E~119°E,14°N~23°N)。其比对统计结果列于表 3。
| Jason-2 - Jason-1 | Jason-1 - T/P | |||
| 差值均值 | 标准偏差 | 差值均值 | 标准偏差 | |
| 渤 海 | 7.95 | ±2.63 | 9.99 | ±4.35 |
| 黄 海 | 7.26 | ±2.50 | 9.04 | ±4.15 |
| 东 海 | 7.44 | ±2.32 | 8.46 | ±2.77 |
| 南 海 | 6.56 | ±2.52 | 8.53 | ±2.87 |
| 中国近海 | 7.33 | ±2.86 | 8.77 | ±3.35 |
由表 3可以看出,3颗卫星数据在中国近海及邻域的平均偏差均小于全球的偏差值。这是因为文献[6, 11]中所得到的偏差结果为使用地球物理环境偏差改正之前的原始观测值,而本文所得结果是建立在使用相应改正模型的基础之上;另一方面,三代卫星测高仪的测量结果在有效波高测量方面存在偏差,且在全球的偏差分布不均匀[27],我国海域附近的偏差相比全球较小,说明三代测高仪在该区域的系统差较小。若在此区域使用全球偏差值,会对海平面异常时间序列的连续性造成较大影响。且其在不同海域的平均偏差值也不同,最大相差超过1 cm,显然,对不同海域使用不同的改正值是非常必要的,否则会人为引入误差,从而影响数据的连续性和精度。在下文所得的时间序列中,将对不同海域采用由表 3得出的平均偏差值,从而建立3颗卫星海平面变化连续时间序列。
4 海平面异常序列 4.1 各海域海平面异常序列本文利用T/P卫星海平面观测值求取中国近海及邻域的沿轨迹平均海平面高,再以此为基准,利用各卫星沿轨迹观测值求取各卫星沿轨迹海平面异常序列。对某区域各周期的海平面异常取空间平均,即可得到该区域海平面异常时间序列。取空间平均时,纬度为φ的点采用如下加权公式[28]
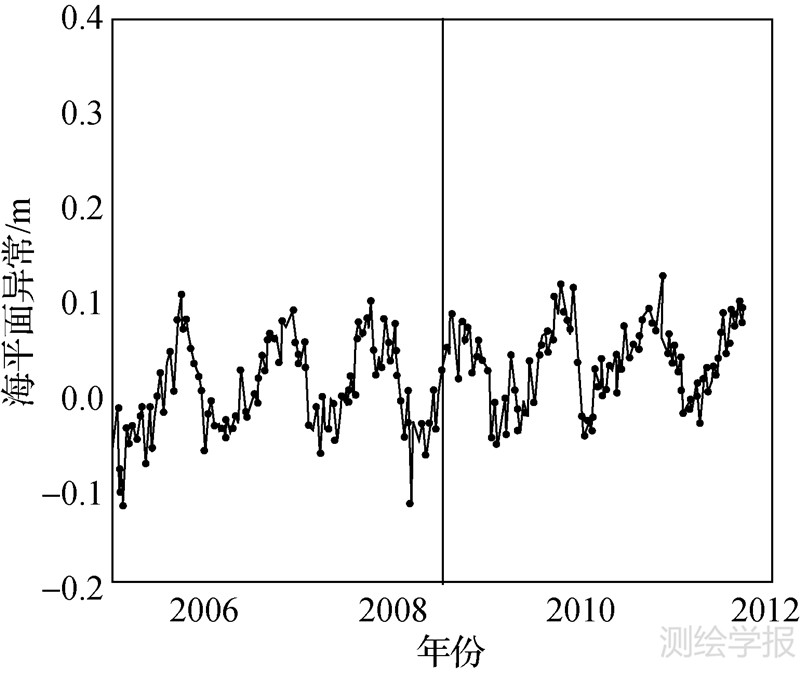
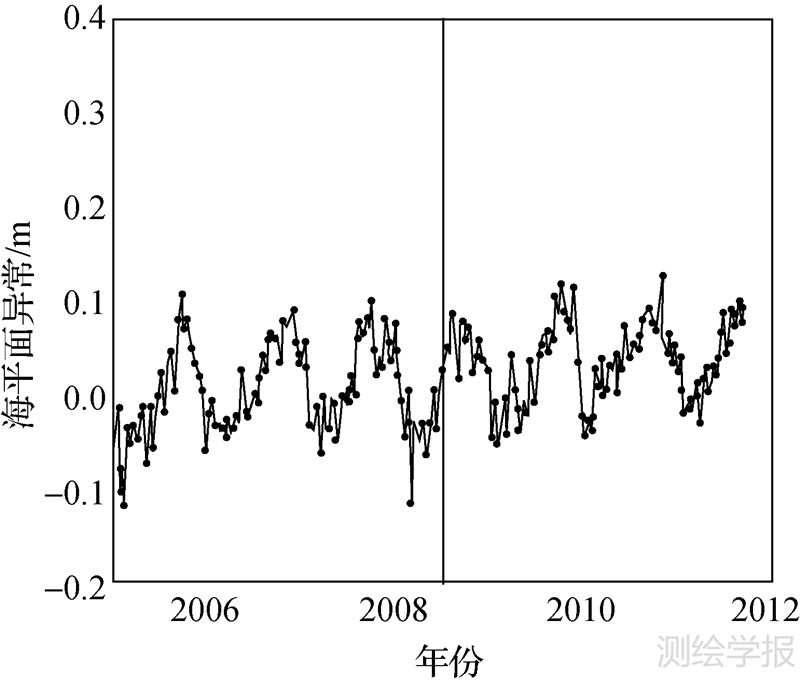
式中,i为卫星的轨道倾角,对于本文中的3颗卫星,i=66°。为了说明不同海域使用不同改正值的必要性,以渤海海域为例,使用表 3列出的渤海海域改正值以及中国近海改正值分别得到的基于Jason-1和Jason-2数据海平面异常序列如图 4和图 5所示(图中竖线为Jason-1与Jason-2数据分界线)。
|
| 图 4 使用渤海海域改正值结果 Fig. 4 Jason-1 and Jason-2 SLA series with correction value in Bohai area |
|
| 图 5 使用中国近海海域改正值结果 Fig. 5 Jason-1 and Jason-2 SLA series with correction value in China Sea area |
由图 4和图 5可以看出,在渤海海域使用中国近海海域改正值所产生的时间序列在两颗卫星数据分界处存在跳变,虽然量级不大,但是对后续的线性拟合会造成约0.5 mm/a的影响,为了数据的连续性以及研究的严密性,使用特定区域的改正值是非常必要的。
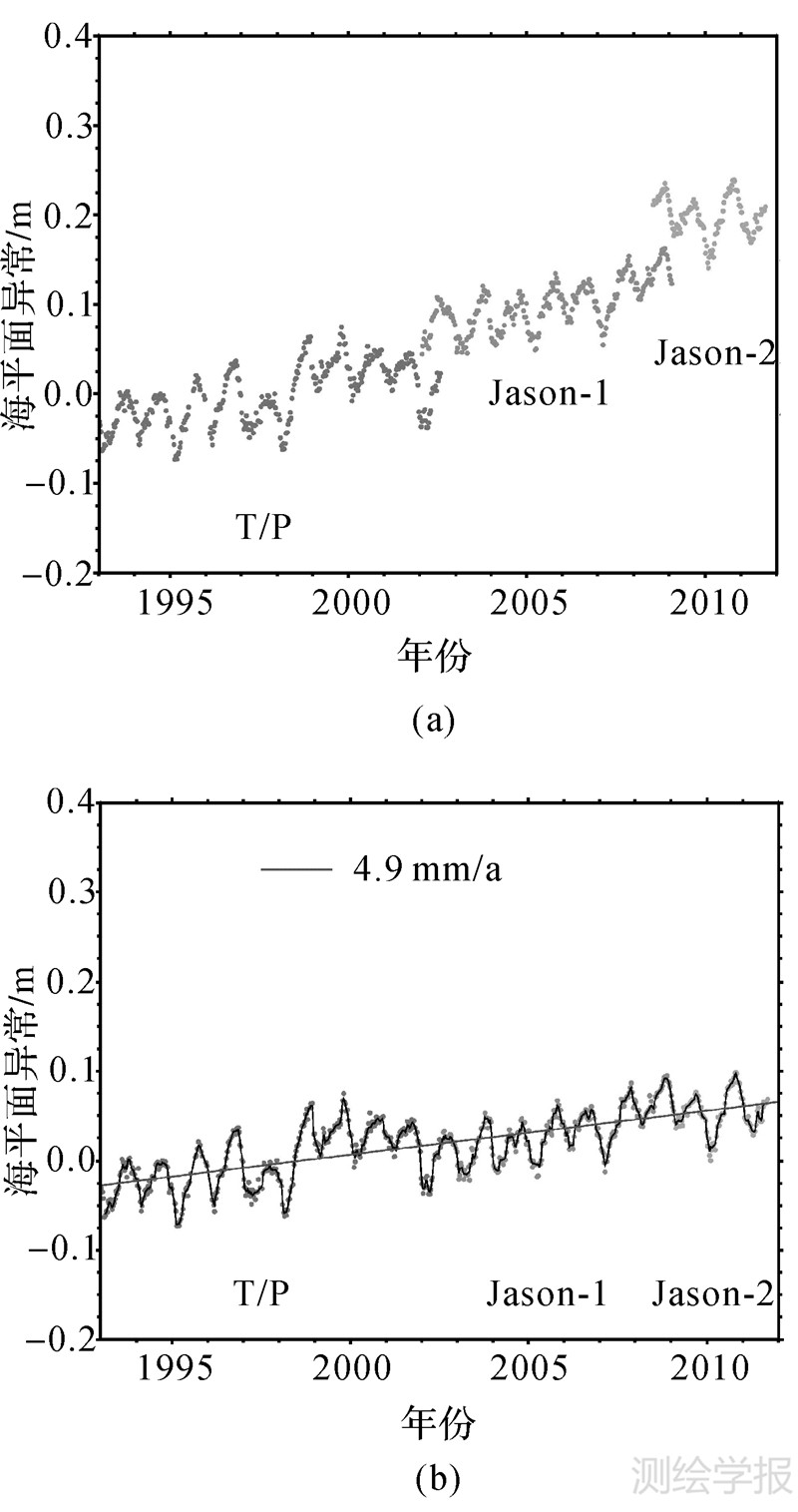
图 6是3颗卫星数据经过空间平均后的中国近海海平面异常序列。从图 6(a)可以明显看出,3组海平面异常序列存在跳变现象,若直接对其进行线性拟合,所得结果必然会存在较大偏差,故有必要对3颗卫星数据之间存在的系统差进行修正。对Jason-1和Jason-2序列采用表 2所列偏差值进行修正,得到中国近海及邻域海平面异常序列如图 6(b)所示。图 6(b)中曲线为60 d平滑后的结果,直线为抗差线性拟合值,其平均变化速率约为4.9 mm/a。
|
| 图 6 中国近海海平面异常时间序列 Fig. 6 SLA time series in China Sea and its vicinity |
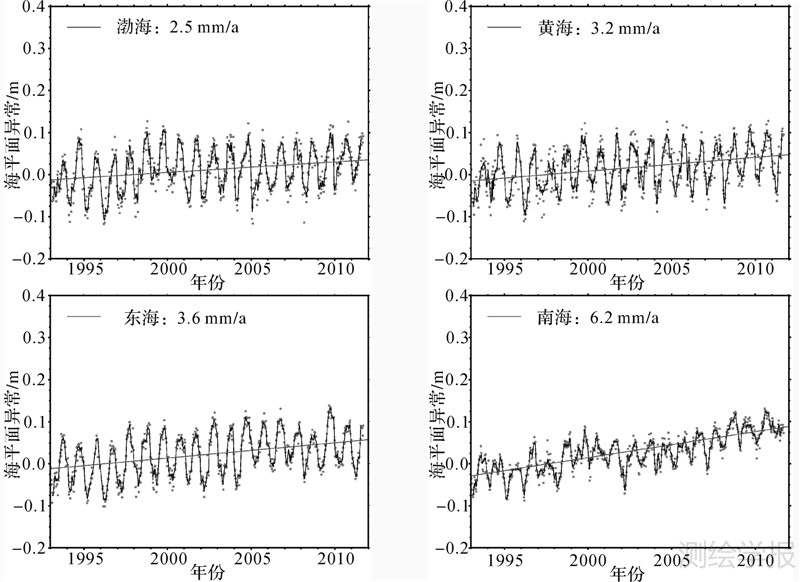
下面计算中国各海域海平面异常序列,并分别采用表 3中的修正值,最终得到中国渤海、黄海、东海及南海的海平面异常序列,如图 7所示。
|
| 图 7 中国各海域海平面异常序列 Fig. 7 SLA time series of China Sea |
分别对其进行抗差直线拟合,其平均变化速率分别约为2.5 mm/a、3.2 mm/a、3.6 mm/a及6.2 mm/a。由图 7可以看出,我国海域海平面变化周期现象明显,且4个海域的海平面变化速率为由北至南逐渐增加,其中南海海平面的上升速率远高于其余3个海域。其原因主要是由于本文采用了最新的Jason-2卫星测高数据,与同使用了Jason-2数据的文献[11]结果较为接近。众所周知,海平面上升呈加速趋势,特别是位于赤道附近的海域,近期的海平面变化更为明显,而Jason-2卫星于2008年发射升空,其观测结果能够更好地反映南海附近海域近期的海平面变化情况,同时也解释了本文结果与仅采用T/P与Jason-1卫星测高数据所得成果存在一定差别的原因。
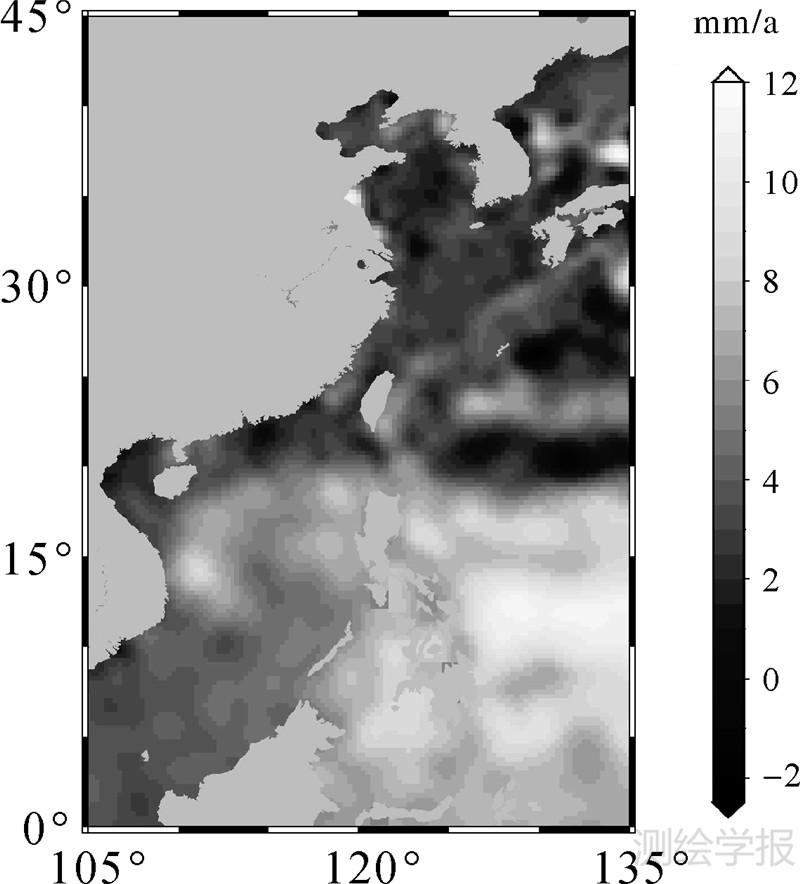
4.2 海平面变化速率分布为了研究中国近海及邻域海平面上升速率分布情况,将3颗卫星的海面高观测值扣除T/P卫星所得平均海平面,得到3颗卫星正常点的海平面异常序列。逐周期利用Shepard格网化方法将正常点海面高异常值进行格网化处理,得到各周期15′×15′格网海平面异常。每个格网各周期的值形成一个时间序列。逐格网计算其平均变化速率,最终得到中国近海及邻域海平面平均变化速率分布,如图 8所示。
|
| 图 8 区域海平面平均变化速率分布 Fig. 8 Average rising rates in regional areas |
从图 8中可以看出,相对其他3个海域,中国南海海平面变化速率较大,这也符合上文所得结果。同时值得注意的是,中国近海海平面变化高于全球平均变化速率。
5 结束语本文利用3颗连续观测任务的卫星测高数据研究了中国近海及邻域的海平面变化情况。首先在数据预处理的基础上,引入高斯滤波器对测高数据进行粗差探测,算例结果表明该方法对于探测海岛附近的数据粗差具有较好的效果。基于3颗卫星同步运行段的数据,分析得到其在该海域存在的差异改正数:相对T/P卫星,Jason-1卫星数据平均偏差+8.77 cm;相对Jason-1卫星,Jason-2卫星数据平均偏差+7.33 cm;则Jason-2相对于T/P卫星的平均偏差为16.1 cm。利用上述平均偏差值,本文建立了基于18 a卫星测高数据的中国近海及邻域海平面异常连续时间序列。其中Jason-1、Jason-2卫星数据的应用,有效延长了中国近海及邻域海平面异常时间序列的时间跨度,为研究我国近海及邻域海平面的变化情况提供重要参考。对其进行线性拟合,结果显示该海域18年来海平面变化速率约为4.9 mm/a;分别构建中国近海不同海域的海平面异常时间序列,得到渤海、黄海、东海及南海海平面变化速率分别约为2.5 mm/a、3.2 mm/a、3.6 mm/a及6.2 mm/a。该结果与已有研究成果较为接近[11, 13, 15],说明了本文结果的正确性。可以看出,南海海平面上升速率远高于其余3个海域,同时远高于全球平均水平;黄海、东海的海平面变化与全球变化水平基本一致,而渤海海平面变化低于全球水平。对各周期海面高数据进行格网化处理,得到不同周期中国近海及邻域15′×15′格网海平面高,分别解算出海平面异常后,逐格网构建其海平面异常时间序列,并对每个格网的序列进行线性拟合,最终得到每个格网近18年来的海平面变化速率,即该海域18年间海平面变化速率分布。计算结果表明,中国近海海平面变化速率与全球平均水平一致,而其邻海海平面的变化速率远高于全球平均水平,菲律宾群岛附近海面的平均上升速率甚至超过了10 mm/a,是全球平均水平的3倍。另外,低纬度地区海面的上升速率明显高于高纬度地区。
我国海岸线较长,覆盖纬度范围大,不同地区的海平面变化情况有较大区别,相比基于验潮站数据的海平面监测,利用卫星测高数据进行海平面变化的监测对于不同地区的对比分析能起到事半功倍的效果。
| [1] | FU L L, CHRISTENSEN E J, YAMARONE C A, et al Topex/Poseidon Mission Overview[J]. Journal of Geophysical Research: Oceans, 1994, 99(C12): 24369-24381. |
| [2] | FU L L. Minutes of the Joint Jason-1 and TOPEX/Poseidon Science Working Team Meeting[R]. Keystone: Jet Propulsion Laboratory, 2002. |
| [3] | LAMBIN J, MORROW R, FU L L, et al. The OSTM/Jason-2 Mission[J]. Marine Geodesy, 2010, 33(1): 4-25. |
| [4] | ANZENHOFER M, GRUBER T. Fully Reprocessed ERS-1 Altimeter Data from 1992 to 1995: Feasibility of the Detection of Long Term Sea Level Change[J]. Journal of Geophysical Research, 1995, 103(C4): 8089-8112. |
| [5] | URBAN T J. The Integration and Application of Multi-satellite Radar Altimetry[D]. Austin: University of Texas, 2000. |
| [6] | BECKLEY B D, ZELENSKY N P, LUTHCKE S B, et al. Towards a Seamless Transition from Topex/Poseidon to Jason-1[J]. Marine Geodesy. 2004(27): 373-389. |
| [7] | BONNEFOND P, EXERTIER P, LAURAIN O, et al. Absolute Calibration of Jason-1 and Jason-2 Altimeters in Corsica during the Formation Flight Phase[J]. Marine Geodesy, 2010, 33(1): 80-90. |
| [8] | ERIC W L, NEREM R S, GARY T M. Calibration of TOPEX/Poseidon and Jason Altimeter Data to Construct a Continuous Record of Mean Sea Level Change[J]. Marine Geodesy, 2004, 27(1): 79-94. |
| [9] | MOHAMMED A A. Sea Level Variability of the Arabian Sea and Its Gulfs from Tide Gauges and Satellite Altimetry[D]. Melbourne: Florida Institute of Technology, 2007. |
| [10] | MARCOS M, TSIMPLIS M N. Coastal Sea Level Trends in Southern Europe[J]. Geophysical Journal International, 2008, 175(1): 70-82. |
| [11] | BECKLEY B D, ZELENSKY N P, HOLMES S A, et al. Assessment of the Jason-2 Extension to the Topex/Poseidon, Jason-1 Sea-Surface Height Time Series for Global Mean Sea Level Monitoring[J]. Marine Geodesy, 2010, 33(1): 447-471. |
| [12] | MOHAMMED A, PHILIPPS S, PICOT N, et al. Jason-2 Global Statistical Assessment and Cross-calibration with Jason-1[J]. Marine Geodesy, 33(1): 162-185. |
| [13] | DONG Xiaojun, HUANG Cheng. Monioring Global Mean Sea Level Variation with TOPEX/Poseidon Altimetry[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 266-272. (董晓军, 黄珹. 利用Topex/Poseidon卫星测高资料监测全球海平面变化[J]. 测绘学报, 2000, 29(3): 266-272.) |
| [14] | WANG Yong, XU Houze, ZHAN Jingang, et al. Complex Principle Component Analysis of Sea Level Variability over China Seas from TOPEX/Poseidon Altimetry[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 438-443. (詹金刚, 王勇, 许厚泽, 等. 中国近海TOPEX/Poseidon卫星测高海平面变化的CPCA分析[J]. 测绘学报, 2001, 30(2): 173-178.) |
| [15] | ZHAN Jingang, WANG Yong, XU Houze, et al. The Wavelet Analysis of Sea Level Change in China Sea during 1992-2006[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 438-443. (詹金刚, 王勇, 许厚泽, 等. 我国近海1992-2006年海平面变化的小波分析[J]. 测绘学报, 2008, 37(4): 438-443.) |
| [16] | QIAO Xin, CHEN Ge. A Preliminary Analysis on the China Sea Level Using 11 Years’ TOPEX/Poseidon Altimeter Data[J]. Marine Sciences, 2008, 32(1): 60-64. (乔新, 陈戈. 基于11年高度计数据的中国海海平面变化初步研究[J]. 海洋科学, 2008, 32(1): 60-64.) |
| [17] | WANG Guodong, KANG Jiancheng, LIU Chao, et al. Analysis and Prediction of Sea-level Change Multi-scale Cycle for East China Sea[J]. Advances in Earth Science, 2011, 26(6): 678-686. (王国栋, 康建成, 刘超, 等. 中国东海海平面变化多尺度周期分析与预测[J]. 地球科学进展, 2011, 26(6): 678-686.) |
| [18] | JIANG Weiping, LI Jiancheng, WANG Zhengtao. Determination of Global Mean Sea Surface WHU2000 Using Multi-Satellite Altimetric Data[J]. Chinese Science Bulletin, 2002, 47(19): 1664-1668. |
| [19] | JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-altimetric Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723-729. (金涛勇, 李建成, 姜卫平, 等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报, 2011, 40(6): 723-729.) |
| [20] | AVISO. DT CorSSH and DT SLA Product Handbook[EB/OL]. Ramonville: AVISO, 2005[2010-11-12]. http://argonautica.jason.oceanobs.com/documents/donnees/tools/dt_corssh_dt_sla_products.pdf |
| [21] | SANDWELL D T, SMITH W H F. Marine Gravity Anomaly from Geosat and ERS-1 Satellite Altimetry[J]. Journal of Geophysical Research, 1997, 102(B5): 10039-10054. |
| [22] | HE Yu. Common Numercial Algorithm and Program(C++ Edition)[M]. Beijing: Posts & Telecom Press, 2003 (何渝. 计算机常用数值算法与程序(C++ 版)[M]. 北京: 人民邮电出版社, 2003.) |
| [23] | HWANG C, SHUM C, LI J. Satellite Altimetry for Geodesy, Geophysics and Oceanography[M]. New York: Springer, 2004: 59-66. |
| [24] | KRYSTEK M. A Fast Gauss Filtering Algorithm for Roughness Measurements[J]. Precision Engineering, 1996, 19(2-3): 198-200. |
| [25] | GEUSEBROEK J M, SMEULDERS A W M, WEIJER J. Fast Anisotropic Gauss Filtering[J]. IEEE Transactions on Image Processing, 2003, 12(8): 938-943. |
| [26] | CHEN Junyong, LI Jiancheng, CHAO Dingbo. Determination of the Sea Level Height and Sea Surface Topography in the China Sea and Neighbor by T/P Altimeter Data[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995, 20(4): 321-326. (陈俊勇, 李建成, 晁定波. 用T/P测高数据确定中国海域及其邻海的海面高及海面地形[J]. 武汉测绘科技大学学报, 1995, 20(4): 321-326.) |
| [27] | DORANDEU J, ABLAIN M, FAUGERE Y, et al. Jason-1 Global Statistical Evaluation and Performance Assessment Calibration and Cross-calibration Results[J]. Marine Geodesy, 2004, 27(3): 345-372. |
| [28] | ZHAI Guojun, OUYANG Yongzhong, HUANG Motao, et al. The Weighting in Mean Sea Level Computation Using Altimeter Data[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(2): 103-106. (翟国君, 欧阳永忠, 黄谟涛, 等. 测高数据在计算海平面时的取权[J]. 武汉测绘科技大学学报, 1999, 24(2): 103-106.) |