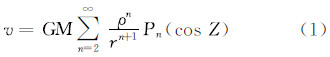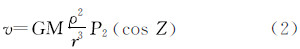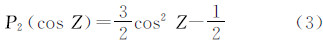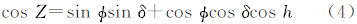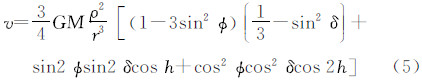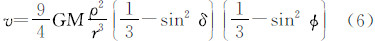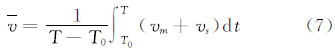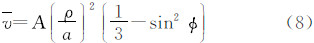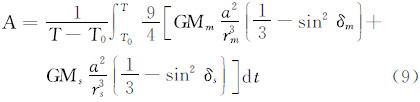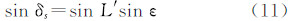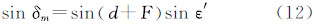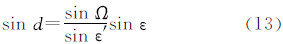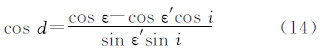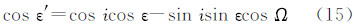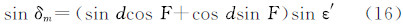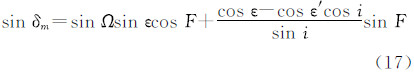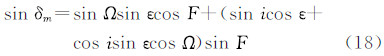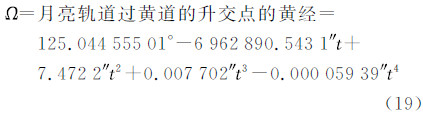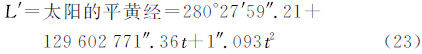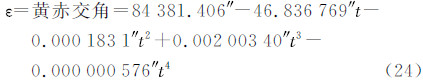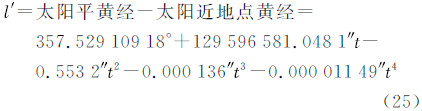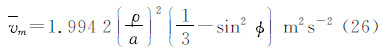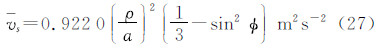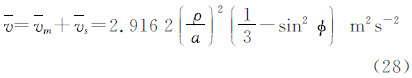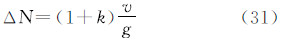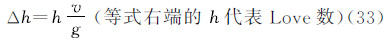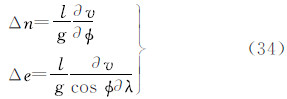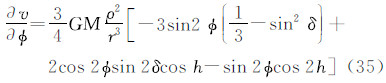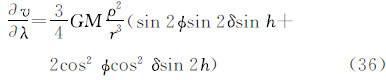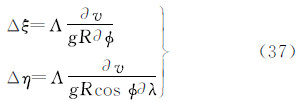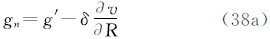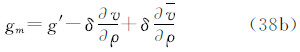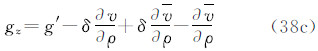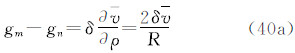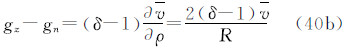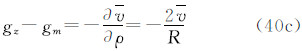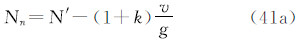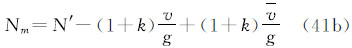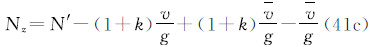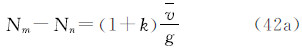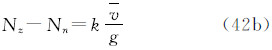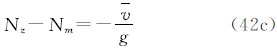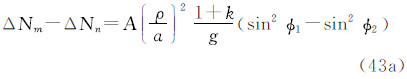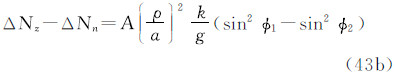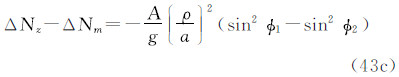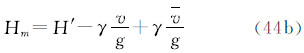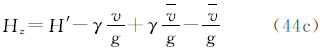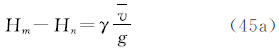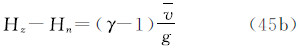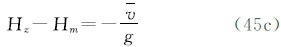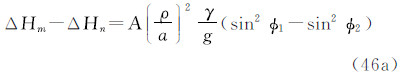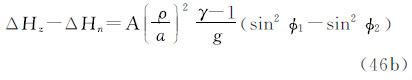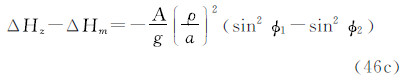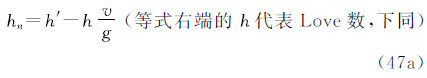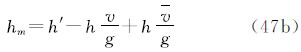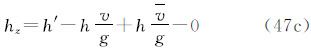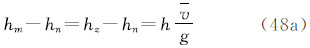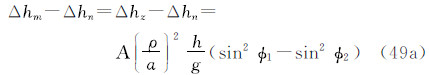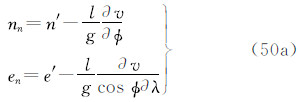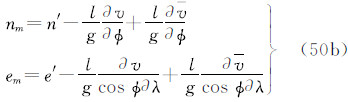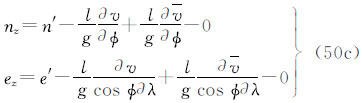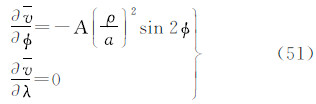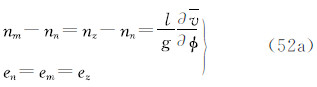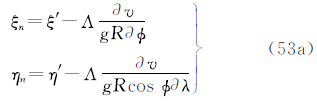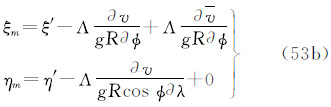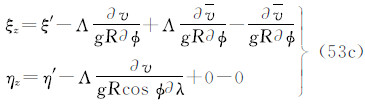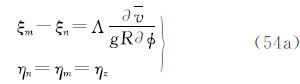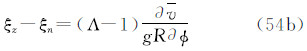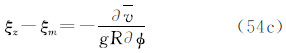2. 地理信息工程国家重点实验室,陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
1 引 言
固体地球在外部天体引潮力作用下产生形变和引力位变化,叫做地球潮汐。地球对于外部天体引潮力的响应像一弹性体。在地球附近的引力位,除地球本身质量产生的引力位之外,还叠加一个外部天体产生的引潮位。引潮位引起地球质量重新分布,使地壳产生附加形变,从而产生一个形变位(deformation potential)。地球潮汐对大地观测的影响,除引潮位导致的直接影响外,还包括因形变位产生的间接影响。
引潮位用球谐展开式表示。地球潮汐的主项2阶项的频率分布于0周/d、1周/d和2周/d附近的3个频带,分别称作长周期、周日和半日潮汐带。在长周期潮汐中,有一个零频率潮汐,或称永久潮汐。无论直接影响,还是间接影响,都包含依赖时间的周期潮汐和与时间无关的永久潮汐。表现为正弦波形式的周期波通过时间平均可以平滑掉,而表现为sin2δ形式的长周期波在一定时段内之时间平均,对一确定地点却是一个常量。这一常量与时间无关项合成永久潮汐或零频率潮汐。永久潮汐对重力的影响会达到71 μGal(1 Gal=1 cm/s2),对大地水准面高和大地高的影响分别会达到26 cm和12 cm。另外,永久潮汐也是定义和实现几何参考基准和垂直基准所必须考虑的因素。这些都是关注永久潮汐的原因所在。
当今测量技术的发展使得人们很容易获得厘米级精度的测量,以前往往被忽略的潮汐改正,已经再也不可忽略了,所以地球潮汐(包括永久潮汐)对于现代大地测量显得特别重要。永久潮汐是一个老话题,有许多文献可以参考[1, 2],然而实践中对于永久潮汐的处理并非是完善无缺的,研究永久潮汐仍不失其实际意义。本文首先研究了永久潮汐位,其次给出了大地观测的3种潮汐值表示式及其互相关系,最后讨论了3种潮汐系统的性质、特点及它们在大地测量中的使用。文章的新颖之处在于用简单明了的方法导出了永久潮汐位的数值表示式,从潮汐系统的定义又直接导出了重力、大地水准面高、大地高等观测量的3种潮汐值表示式及其互相转换关系。
2 永久潮汐位在地壳上一点P,外部天体(月亮、太阳等)的引潮位,可以表示为球谐级数[3, 4, 5, 6, 7]
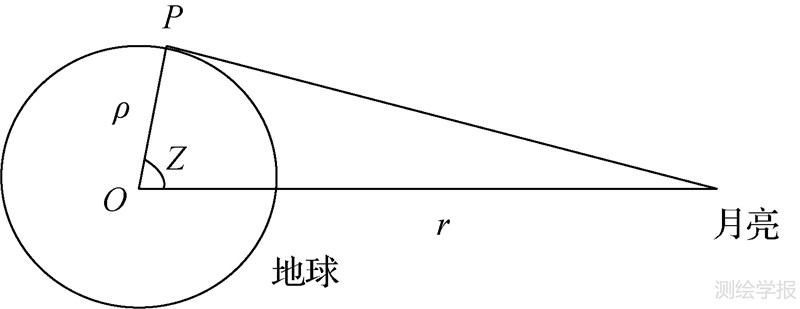
式中,GM为外部天体的引力常数; ρ为研究点P的地心向径;r为天体的地心向径,Z为天体的地心天顶距(见图 1),Pn(cos Z)为n阶勒让德多项式。
|
| 图 1 地球潮汐问题的几何 Fig. 1 Geometry of the earth tide problem |
简单计算表明,若令月亮的GM/r3值等于1,则太阳的相应值是0.46,金星是5×10-5,木星是6×10-6。所以一般仅考虑日月潮汐。式(1)的级数随n的增加而迅速收敛,例如,对于月亮,ρ/r2≈4.3×10-8,ρ2/r3≈7.1×10-10,所以在研究中,式(1)取至n=2(事实上,对于永久潮汐研究,取n=2即可,因为当n=3时,永久潮汐为0)。因此,将引潮位简单写成
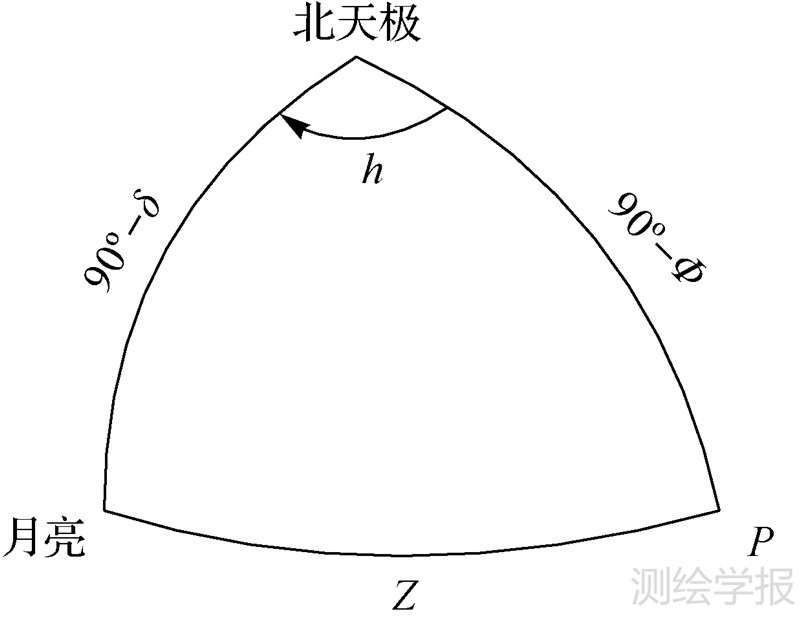
式中 式中,φ代表P点的地心纬度;δ和h代表天体的赤纬和地方时角(图 2)。
|
| 图 2 球面三角形 Fig. 2 Spherical triangle |
将式(3)代入式(2),并使用式(4),可得
此式表明,一个点的潮汐位是天体坐标r、δ、h的函数。在3个坐标中,r和δ变化较慢,h变化最快。式(5)右端方括号内的第1和第2项由地球自转引起,分别为周日项和半日项,在一日和半日内的均值分别等于0(忽略在此期间r和δ的变化影响),因此对永久潮汐不产生贡献,下文将不再进一步讨论。剩下的第1项(仍以v表示)
通常称为长周期项。该项稍经变换可细分为两项:第1项等于(-1/3+sin2φ)/6,是随纬度而异的常数项,是永久潮汐的当然贡献者;第2项等于(1/3sin2φ)(cos 2δ)/2,是真正的长周期项,其周期为δ的变化周期之半,具体而言,对于月亮为半月,对于太阳为半年。注意,第2项在任一时间段内的均值都不等于0(除非在φ=35.26°处),因而也是永久潮汐的贡献者。从物理上说,在考虑的时间段(时段长度理论上应为所有周期潮汐的周期之公倍数)内,外部天体引潮位的平均值即是永久潮汐位。因此,在时间区间[T0,T]内的永久潮汐位可以表示为 式中,m代表月亮;s代表太阳。考虑到式(6),引入地球赤道半径a,式(7)可以写成
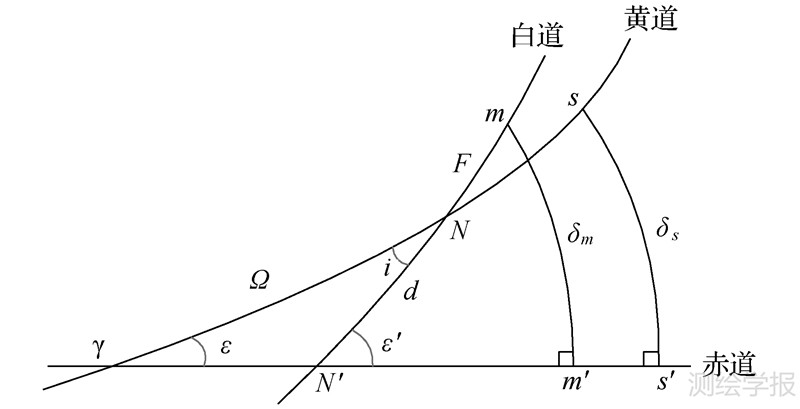
式中,A代表永久潮汐的振幅。 式中,天体地心向径r(rm和rs)用下式计算 式中,a代表天体轨道的半长径;e代表轨道的偏心率;f代表天体的真近点角。为后面进行A的数值计算,下面推导sinδ之算式。在图 3中,γ代表春分点,m和s分别代表月亮和太阳,δm和δs代表它们的赤纬。在球面直角三角形sγs′中,使用正弦定理,有
式中,L′为太阳平黄经;ε为黄赤交角。当L′= 90°时,δs=ε,δs达到最大。所以δs的变化范围为〈-ε,+ε〉。
|
| 图 3 太阳和月亮的轨道几何 Fig. 3 Geometry of luni-solar orbits |
在球面直角三角形N′mm′中,使用正弦定理
在球面三角形NγN′中,使用正弦定理和角的余弦定理
式中,ε′为月亮轨道对赤道的倾角;d为从N′(月亮轨道与赤道的升交点)至N(月亮轨道与黄道的升交点)的白道弧段;F为从N到月亮m的白道弧段,F = L-Ω;L为月亮的平黄经;Ω为月亮升交点N的黄经;i为白道对黄道的倾角。将sin(d+F)展开,式(12)变成
用式(13)、(14)代替上式中的sin d和cos d,得
用式(15)代替上式中的cosε′,经整理得
由式(12)知,当d+F=90°时,δm=ε′,δm达到最大。由式(15)知,当Ω=0时,ε′=ε+i;当Ω=π时,ε′=ε-i;当Ω=±π/2时,ε′=cos-1(cos icos ε),由于cosi<1,所以此时ε′<ε。于是得知,(ε-i)<ε′<(ε+i),即ε′在(ε±i)的范围变动。月亮升交点大约18.61a沿黄道西退一圈,即升交点黄经Ω在此期间变动360°,而月亮赤纬在此期间按式(18)在±(ε+i)之间变动。月亮赤纬的变化使得所有月亮潮汐的振幅产生所谓“交点调制”[7]。
永久潮汐振幅A是日月引力常数和轨道参数的函数(见式(9))。在振幅A的数值计算中,我们采用下列常数和参数[8, 9, 10]
地球:
引力常数GM=3.986 004 418×1014m3s-2
长半轴a=6 378 136.6 m
月亮:
引力常数GMm= GM×月地质量比 μ( 0.012 300 037 1)=4.902 800 222 216 39×1012 m3s-2
偏心率常数e=0.054 879 905
轨道半长径a=384 747 981 m
倾角常数sin(i/2)=0.044 751 305
式中,t为自2000-01-01T12:00起算的世纪数(1世纪=36 525 d)。太阳:
轨道半长径a=1.000 001 02 AU
天文单位1AU = 149 597 870 700 m
计算潮汐振幅A,要求根据月亮和太阳的有关参数,用式(10)计算月亮和太阳的地心向径r(月亮和太阳的真近点角f分别用式(21)和(25)计算),用式(18)和(11)计算它们的sinδ。
本文计算了6个区间的振幅A。各个区间的起始历元均为T0= 2 000.0,终止历元依次为T= T0+i×18.61 a,i为1到6之间的整数,代表区间号。计算多个区间的目的在于进行互相比较,并得到更精确的结果。对于每一区间[T0,T],用自适应Simpson求积法,计算式(9)的定积分,并取该区间的均值。各区间的数值结果列在表 1。
| m2s-2 | ||||||
| T-T0/a | 1×18.6 | 2×18.6 | 3×18.6 | 4×18.6 | 5×18.6 | 6×18.6 |
| 月亮项振幅 | 1.988 9 | 1.997 3 | 1.990 4 | 1.995 9 | 1.996 7 | 1.996 1 |
| 太阳项振幅 | 0.922 4 | 0.924 0 | 0.918 1 | 0.921 4 | 0.922 4 | 0.923 7 |
| 总潮汐振幅 | 2.911 3 | 2.921 3 | 2.908 5 | 2.917 3 | 2.919 0 | 2.919 7 |
将6个区间之振幅值视为等权,取它们的均值作为最后结果,即
月亮项振幅=1.994 2(15)m2s-2
太阳项振幅=0.922 0(9)m2s-2
总的永久潮汐振幅=2.916 2(21) m2s-2,这里圆括号内的数字代表标准差(以小数最后一位为单位)。于是得永久潮汐位的数值表示式
式中,ρ为计算点的地心向径; φ为计算点的地心纬度;a为地球赤道半径。式(26)~(28)之参考历元为2 000.0。文献[11, 12]给出3个18年永久潮汐的振幅(参考历元1900.0)分别是:H0=0.314 46;0.314 52;0.314 55。IERS约定给出的振幅值为[8, 9]:H0=0.314 60 m。以m为单位的H0乘以(3/2)(5/4π)1/2ge(赤道半径处的g =9.798 286 85 ms-2)转换成位的单位[8, 9],得H0=2.916 6 m2s-2。本文结果与这一数值相差0.000 4 m2s-2。造成差异原因很多,在数据方面采用了“平”轨道参数,而且月亮轨道半长径、偏心率、轨道倾角等参数采用了参考历元J2 000.0的常数值;方法方面差异更大,本文采用的数值积分法也是一种近似。然而,无论如何,本文得到的数值是相当精确的,与IERS约定值之差异所导致的大地水准面高之差不会超过0.05 mm,重力值之差不会超过0.2 nGal。
3 潮汐系统及其互相转换固体地球对潮汐力的反应像一弹性体。一个球对称、无旋转、无海洋的地球之潮汐反应可以通过对潮汐位级数项施以无量纲的love数h、k、l(l也叫Shida数)来描述[6, 7]。潮汐引起大地观测的变化可以通过潮汐位v(包括永久成分和时变成分)施以h、k、l或它们的组合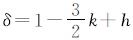 (重力因子),γ=1+k-h(缩小因子),Λ=1+k-l来描述[4, 5, 6, 7]。Love数实际上与球谐的阶数n有关,这里我们仅关心2阶Love数。对标准地球模型PREM,h=0.603 2,k=0.298 0,l=0.083 9[7];δ=1.156 2,γ=0.694 8,Λ=1.214 1。
(重力因子),γ=1+k-h(缩小因子),Λ=1+k-l来描述[4, 5, 6, 7]。Love数实际上与球谐的阶数n有关,这里我们仅关心2阶Love数。对标准地球模型PREM,h=0.603 2,k=0.298 0,l=0.083 9[7];δ=1.156 2,γ=0.694 8,Λ=1.214 1。
关于地球潮汐对大地观测量之影响,可以查阅教科书[4, 5, 6, 7]。这里不加推导,径直引出其表示式。
(1)重力g
式中 式中,R代表地球平均半径。(2)大地水准面高N
(3)正高H
(4)大地高h(垂直位移)
(5)南北/东西位移n/e
式中(6)天文垂线偏差(地面垂线偏差)ξ/η
注意,上面诸式中的v为全部引潮位,既包括时变成分,也包括永久成分;包括直接影响,也包括间接影响。
由于潮汐的影响,大地观测分为无潮汐的(non-tidal或tide-free),平均潮汐的(mean- tide)和零潮汐的(zero-tide)[1, 13]。瞬时大地观测包括所有潮汐影响。从瞬时大地观测除去全部潮汐影响(包括时间依赖成分和永久潮汐),称为大地观测的无潮汐值;从瞬时大地观测除去潮汐的时变成分,保留全部永久成分(包括直接影响的永久成分和间接影响的永久成分),称为大地观测的平均潮汐值;从平均潮汐值中除去直接影响的永久成分,仅保留间接影响的永久成分,称为大地观测的零潮汐值[1, 13, 14]。根据三种潮汐值的定义,对任何大地观测,我们容易直接导出它们的无潮汐值、平均潮汐值和零潮汐值表示式。现将3种潮汐系统中6类大地观测的具体表示形式归纳如下。注意,下面式中凡带“′”的量代表瞬时观测量(例如,g′代表瞬时重力观测值),带下标“n”的量为无潮汐值(例如,gn代表无潮汐重力值),带下标“m”的量为平均潮汐值(例如,gm代表平均潮汐重力值),带下标“z”的量为零潮汐值(例如,gz代表零潮汐重力值);式中v代表全部潮汐(包括时变成分和永久成分)的引潮位(用式(5)计算),v 代表永久潮汐位(用式(7)或(28)计算)。
(1)重力g
式中那么,3种重力潮汐值之间的关系为
(2)大地水准面高N
值得说明,当说到大地水准面高时,这里已假设参考椭球面是固定的,即参考椭球面被看作一个纯几何面,其长半轴和扁率已经固定了。(实际上,从概念上说,参考椭球的长半径和扁率,也因潮汐系统而有不同的数值。这里不考虑这种情况。)
对应不同的潮汐系统,大地水准面分为无潮汐大地水准面(tide-free geoid)、平均大地水准面(mean geoid)和零大地水准面(zero geoid)。
3种潮汐系统的大地水准面高之间的关系为
注意到式(28),得到1、2两点的大地水准面高之差(在2-1意义上)的3种潮汐值之间的关系:
(3)正高(水准高)H
值得指出,正高的无潮汐值代表相对无潮汐大地水准面的高度,平均潮汐值代表相对平均大地水准面的高度,零潮汐值代表相对零大地水准面的高度。
3种潮汐系统的正高之间的关系如下
注意到式(28),得到1、2两点的正高之差(在2-1意义上)的三种潮汐值之间的关系
(4)大地高h
值得指出,大地高代表地壳的高度;无潮汐大地高值代表无潮汐地壳在椭球上的高度,平均潮汐大地高值代表平均地壳在椭球上的高度,零潮汐大地高值代表零地壳在椭球上的高度。注意,零地壳与平均地壳是等同的。
3种潮汐值之间的关系为
注意到式(28),得到1、2两点的大地高之差(在2-1意义上)的三种潮汐值之间的关系:
(5)南北/东西分量坐标n/e
式中3种潮汐系统的水平坐标之间的关系为
式(52)表明,对于水平位移,零潮汐值等于平均潮汐值。零地壳与平均地壳是等同的。
(6)天文垂线偏差ξ/η
3种潮汐系统的垂线偏差之间的关系为
式(38)~(54)是6类观测量的不同潮汐值形式及其转换关系。关于重力、正高、大地水准面高和大地高的相关式子亦见文献[1]。为使读者了解永久潮汐的量级,表 2列出了6类大地观测的永久潮汐影响的最大值和最小值。这些值实际上代表了大地观测的平均潮汐改正。
| 观测量 | 最大值 | 最小值 |
| 重力/μGal | 35(在赤道) | -71(在两极) |
| 大地水准面高/m | 0.13(在赤道) | -0.26(在两极) |
| 正高/m | 0.07(在赤道) | -0.14(在两极) |
| 大地高/m | 0.06(在赤道) | -0.12(在两极) |
| 南北水平位移/m | -0.02(在纬度±45°) | 0(在两极和赤道) |
| 子午垂线偏差/(″) | -0.01(在纬度±45°) | 0(在两极和赤道) |
地球潮汐对大地观测的影响,包括直接影响和间接影响,两种影响都包括时变成分和永久成分。为了处理地球潮汐,人们将大地观测分为无潮汐值、平均潮汐值和零潮汐值。
在本文所述的无潮汐系统中,所有的潮汐成分用一模型消除了。模型用的Love数h、k和Shida数l,仅适于弹性体,适于短周期性成分,其名义值为h=0.60,k=0.30,l=0.08。这种无潮汐系统,通常叫做常规无潮汐系统[8, 9, 14]。实际上,地球对永久潮汐的响应,并不像弹性体,而更像液体[1]。所以,常规无潮汐系统并不是真正的无潮汐系统。对于液体的Love数,hf =1.93,kf =0.93[1],由此得到γf=0,δf=1.53。这意味着,计算真重力或真大地水准面应该用δ≈1.53,而不是用1.16。但是这样的问题是,永久潮汐因子δ不可能由任何观测确定,这意味着,真正的无潮汐系统是不可观测的[1, 8, 9]。再者,如果要真地消除永久潮汐形变,地球惯性矩、地球旋转速度和离心力都势必改变[1]。所以,真正的无潮汐系统又不可用。
在平均潮汐系统中,全部永久潮汐(包括直接影响中的永久潮汐和间接影响中的永久潮汐)都被保留了。但是,由于保留了直接影响中的永久潮汐,地球位中包括了引潮位,重力中包括了由引潮位产生的永久潮汐引力,这意味着大地水准面之外存在质量,因而用平均重力按Stokes公式计算的大地水准面高就会得出错误结果[15],误差达到72 cm[1]。因而对于与地球重力场有关的量(如重力、大地水准面高),用平均潮汐系统是不合适的。然而,对于以参考于椭球面的大地高表示的地壳,不包含直接影响,所以平均地壳与零地壳是等同的,即平均站位移与零重力是对应的。
在零潮汐系统中,直接影响中的永久潮汐除去了,仅保留了间接影响中的永久潮汐。实际上,作为间接影响的形变位,不可能从静态地球位中区分出来[2],就是说,静态地球位中,包含了间接影响中的永久潮汐,所以间接形变的永久部分不应从观测和参数中除去。由于直接影响中的永久成分被除去了,相当于外部天体的质量不存在了。这样用零重力按Stokes计算大地水准面高,就会得到正确的结果。
上面已简要说明了3种潮汐系统的性质。那么为什么会有这么多种潮汐系统?大地测量到底应该使用哪一系统?在实践中,不同国家或不同地区或不同时期,对潮汐的影响确实存在着不同的处理方式,例如,有将潮汐影响完全去除的,也有对潮汐不管不问的(这种情况实际上接近平均潮汐),等等。当比较不同国家或不同地区或不同时期的测量结果时,可能会遇到不同潮汐系统之间的互相转换。
使用何种潮汐系统,对于低精度应用,似乎并不那么重要;然而对于高精度应用却是至关重要的。要知道,水准测量、高程系统、三维参考系、大地水准面模型和潮汐改正都是互相关联的,它们应该使用一致的,而不是不一致的潮汐系统(否则,当具有确定的物理和/或几何关系的大地量在互相转换比较时,就可能产生较大的不符值)。对大地测量而言,如前所述,应该使用零重力、零大地水准面、零地壳(=平均地壳),即重力、大地水准面高、正高(或正常高)和大地高都用零潮汐值。从实践观点来看,这也是正确执行用GNSS大地高和大地水准面高检测水准的必要条件。为了统一处理诸如重力和站位置等各种大地量的需要,1983年18届IAG大会16号决议建议[2, 8, 9],由地球永久屈服(permanent yielding)引起的间接影响不要除去,就是说,对于与地球位有关的量用零潮汐值,对于与站位移有关的量用平均潮汐值(注意,对站位移,零潮汐值和平均潮汐值是一回事)。这一建议的基本出发点是,不论几何观测量,还是物理观测量,都要求用零潮汐系统。
关于潮汐系统,在实践中人们可能遇到的问题是:一是国际大地测量界在分析空间大地测量数据时并未认真执行IAG大会16号决议,在现有的空间定位和定轨软件中,潮汐影响用模型都消除了,结果得到的站坐标实际上属于常规无潮汐系统。为此,在IERS约定中给出了由常规无潮汐坐标转换为平均潮汐坐标的式子[8, 9],亦见本文的式(48a)、(49a)和(52a);二是根据定义,大地水准面与平均海水面重合,所以在海洋上大地水准面应是平均大地水准面,而且它对海洋学研究(如海面地形研究)也是适宜的。然而,垂直基准应该用零潮汐系统,即在陆地用零大地水准面。这样人们就可能遇到陆海两种潮汐系统的大地水准面。在陆海大地测量数据联合处理或陆海大地水准面拼接时,应该注意这一情况。
| [1] | EKMAN Martin. Impacts of Geodynamic Phenomena on Systems for Height and Gravity[J]. Bulletin Geodesique, 1989, 63(3):281-296. |
| [2] | RAPP R H, NEREM R Steven, SHUM C K, et al. Consideration of Permanent Tidal Deformation in the Orbit Determination and data Analysis for the Topex/Poseidon Mission[R]// NASA Technical Memorandum 100775.Greenbelt :Goddard Space Flight Center, 1991. |
| [3] | MORITZ Helmut, MULLER Ivan I. Earth Rotation:Theory and Observation[M]. New York: Ungar,1987. |
| [4] | HU Mingcheng, LU Fu. Modern Geodesy: second part[M]. Beijing: Surveying and Mapping Press,1994. (胡明城,鲁福. 现代大地测量学:下册[M]. 北京:测绘出版社, 1994.) |
| [5] | VANICEK P, KRAKISKY E J, Geodesy: The Concepts[M].2nd ed. Amsterdam: Elsevier Science Publishers B V, 1986. |
| [6] | TORGE Wolfgang. Geodesy[M]. 3rd ed. New York: Walter De Gruyter, 2001. |
| [7] | AGNEW D C . Earth Tides[R]. San Diego: University of California San Diego, 1998. |
| [8] | McCARTHY Dennis D, GÉRARD Petit. IERS Technical Note: 32[C] // IERS Conventions 2003, Frankfurt am Main:Verlag des Bundesamts für kartographie und Geodäsie, 2004. |
| [9] | GÉRARD Petit, LUZUM Brians. IERS technical Note: 36[C]//IERS Conventions 2010, Frankfurt am Main: Verlag des Bundesamts für kartographie und Geodsie, 2010. |
| [10] | Zijinshan Astronomical Observatory. The Chinese Academy of Sciences. Chinese Astronomical Almanac for 2005[M]. Bejing: Science Prees, 2004. (中国科学院紫金山天文台. 2005年中国天文年历[M]. 北京: 科学出版社,2004.) |
| [11] | CARTWRIGHT D E, TAYLER R J. New Computations of the Tide-generating Potential[J]. Geophysical Journal Royal Astronomical Society, 1971,23:45-74. |
| [12] | CARTWRIGHT D E, EDDEN Anne C. Corrected Tables of Tidal Harmonics[J]. Geophysical Journal Royal Astronomical Society, 1973,33:253-264. |
| [13] | GROTEN E. Parameters of Common Relevance of Astronomy, Geodesy, and Geodynamics[J]. Journal of Geodesy, 2000, 74(1):134-140. |
| [14] | IHDE Johannes, MÄkinen Jaakko, Sacher Martina. Conventions for the Definition and Realization of a European Vertical Reference System (EVRS)-EVRS Coventions 2007-[EB/OL].[2012-04-16].http://www.bkg.bundde/geoidIS/EVRS/SharedDocs/Downloads/Publications/EVRF Conventions2007 |
| [15] | SMITH Dru. Permanent Tide Systems[EB/OL].[2012-05-01]. http://www.ngs.noaa.gov/GEOID/tidepot.htm/. |