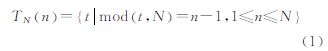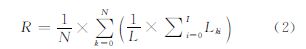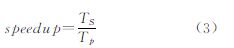2. 武汉大学 资源与环境科学学院,湖北 武汉 430079
2. School of Resources and Environmental Sciences,Wuhan University,Wuhan 430079,China
1 引 言
机载激光雷达(light detection and ranging,LiDAR)点云数据已经广泛应用于数字高程模型(DEM)生成[1]、城市环境三维建模[2]、灾害调查与环境监测[3]等领域。点云数据的滤波过程,即将激光脚点区分为地面点和非地面点,是点云数据处理的关键步骤之一[4]。滤波处理及质量控制所消耗的时间占到整个处理时间的60%~80%[5]。为了提高滤波的精度和效率,目前已经提出了多种滤波处理方法,相关综述可见文献[6]。
经典的机载LiDAR测量数据的滤波方法有不规则三角网渐进加密[7]、稳健线性内插[8]、渐进窗口数学形态学滤波[9]、基于坡度的滤波处理[10]等。不同类别的滤波方法采取了不同的设计策略,其中不规则三角网渐进加密,稳健线性内插这类基于地形表面的滤波方法兼顾了点云激光脚点的上下文地理信息,可以更加真实地区分地面脚点与非地面脚点,滤波结果的数据质量优于其他种类算法[11]。已有的滤波方法依据不同标准有不同的分类,文献[12]根据滤波过程中的重复次数将滤波方法区分为迭代滤波与非迭代滤波,非迭代滤波通过一次性判别完成地面脚点与非地面脚点的区分过程,而迭代滤波则需要通过多次渐进加密运算来完成地形表面的逼近。非迭代滤波的优势在于计算速度较快,但计算结果的精确性不如渐进加密滤波算法[6]。文献[7, 13]提出的不规则三角网渐进加密滤波方法(下文中简称渐进加密滤波)采用了基于地面脚点构建的三角网来拟合地形表面的策略,该方法由不规则三角网构建算法与脚点判别算法迭代复合组成,对城区与森林地区具有较好的适用性,并且应用于商业软件TerraScan[14]。渐进加密滤波方法以计算时间来换取更高的计算精度,随着加密次数的增加,判别过程所需的时间逐渐增加。渐进加密滤波方法的滤波质量较高,因而得到普遍认可,但滤波效率仍然有进一步提高的空间。对于一般的滤波方法而言,点云数据分布形态的复杂性是影响算法处理性能的一个重要因素,如复杂城市形态与不连续性地表[6]。点云数据的分布差异会导致单位面积范围内对应的计算量存在差异,滤波方法的并行优化必须解决由此导致的并行任务间计算量负载不均衡问题。
本文提出一种基于多核处理器的并行渐进加密滤波方法来提高滤波处理效率,其中包括三角网并行构网算法与并行脚点判别算法。并行渐进加密滤波方法对不同分布形态点云数据具有良好的适应性,可以很好地解决计算量分布不均的问题,从而提高算法效率。
2 并行渐进加密滤波方法 2.1 渐进加密滤波方法分析渐进加密滤波方法通过多次迭代执行“地面脚点加密构网——点云脚点判别”过程来区分地面点与非地面点,当加密过程进行到没有新增地面脚点或者加密次数达到预先设定的最大加密次数时结束。完整的渐进加密滤波处理过程可以分为3个阶段:算法初始化(T1),三角网构建(T2)与脚点判别(T3)。表 1为5组不同场景数据的6次串行渐进加密过程的时间分布,Ti代表Ti所占总时间的比例。从表 1看,串行方法中脚点判别过程占整个算法时间的绝大部分,构网所用时间所占比例较小,而初始化时间可以忽略。通过对各次加密滤波的数据量分析发现,首次滤波可以将大部分地面点过滤出来,之后各次滤波所得到的地面点数量迅速减少,相应加密构网所消耗的时间也迅速降低。可见,并行化的关键是三角网构建过程的并行与脚点判别过程的并行,而三角网构建过程中最耗时部分是首次构网。
| 序号 | T1/(%) | T2/(%) | T3/(%) | 点数 |
| 1 | 1.08 | 5.10 | 93.77 | 396657 |
| 2 | 1.12 | 5.50 | 93.31 | 793315 |
| 3 | 1.18 | 7.08 | 91.66 | 1688246 |
| 4 | 1.09 | 5.71 | 93.14 | 2411859 |
| 5 | 1.13 | 6.41 | 92.39 | 3221977 |
| 平均 | 1.12 | 5.96 | 92.85 | — |
渐进加密滤波方法首先需要选择合适的不规则三角网构建算法,然后在三角网算法基础上实现点云脚点的判别与渐进加密过程。因此,被选择的三角网构建算法应该可以实现并行化,且支持以增量方式进行加密。从算法实现原理角度知,分治法具有实现并行化的天然优势。文献[15]系统研究了三角网串行构网算法,发现分治算法相对具有更高的效率与更强的健壮性,算法复杂度在最坏情况下为O(nlogn),并且更能适合不均匀的点云数据分布。文献[16]以开源方式发布的不规则三角网构建库Triangle实现了常规的串行三角网构建算法,其中分治法的效率明显高于其他算法,并且对不均匀分布点云数据具有良好的适应性。Triangle中各种算法具有相同的三角网数据结构,分治法与增量插入法可以结合使用。因此,渐进加密中可以将首次滤波得到地面脚点集合以分治构网算法构网,而后续滤波得到的少量地面点以增量插入法顺序加入到三角网中。
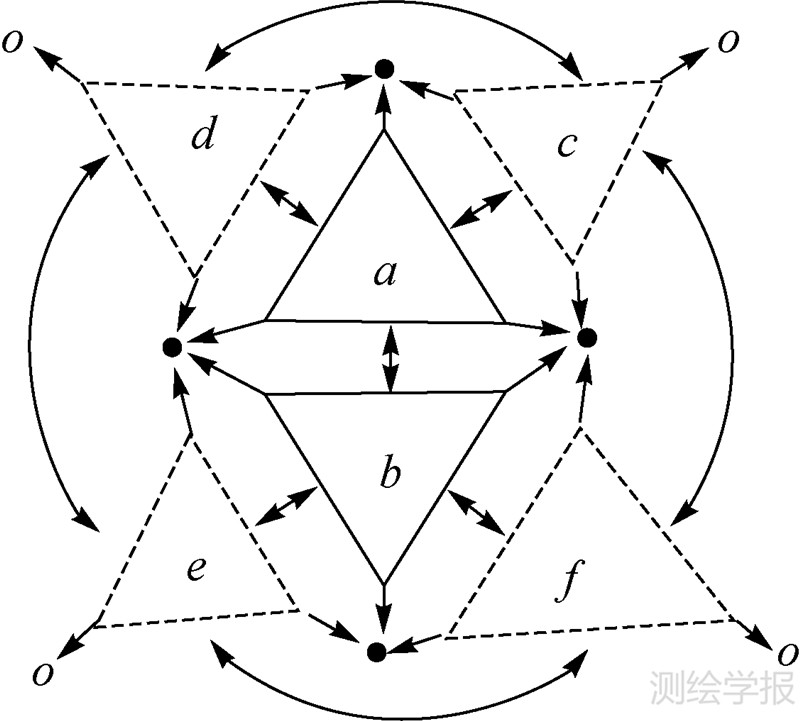
Triangle中的构网算法采用基于三角形的数据结构,通过记录三角形的3个顶点与3条边信息来建立与邻接三角形的拓扑关系,并在三角网边缘用封闭包围的“ghost”三角形来表达。“ghost”三角形均包含的一个处于“无穷远处”顶点,用于辅助从三角网边界边开始遍历三角网。如图 1,三角形a、b为实体三角形,各个实心顶点代表实际坐标点,c、d、e、f为“ghost”三角形,各包含一个的空心顶点坐标。
|
| 图 1 Triangle数据结构 Fig. 1 Data structure of Triangle |
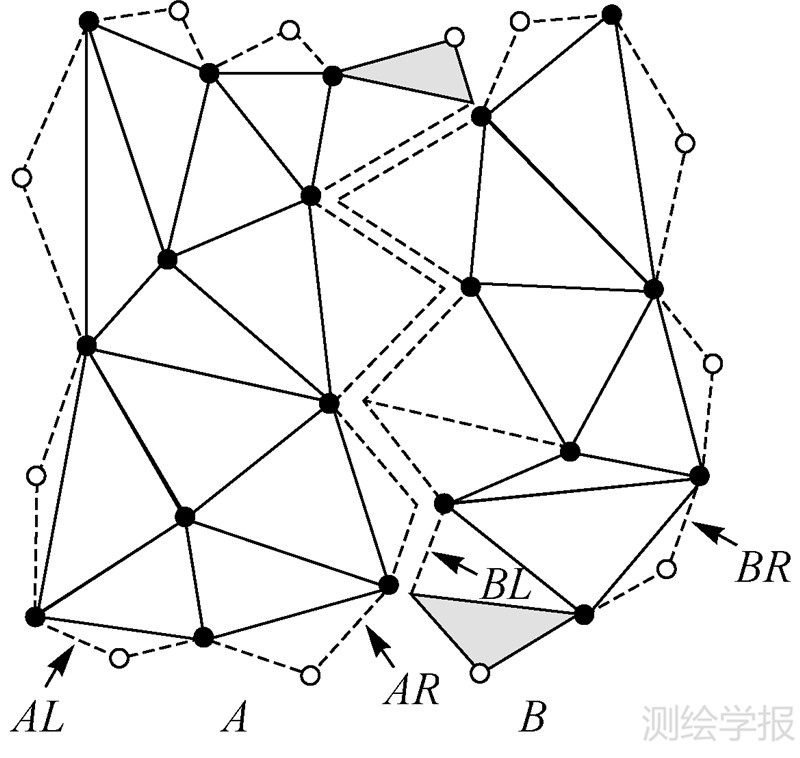
Triangle中的分治构网算法,首先需要对输入点进行横坐标排序(横坐标相同则以纵坐标排序),并剔除掉坐标重复点。然后将输入点递归划分为均等的两份,划分过程直至每份点数为2或者3结束。两点可构建包含一条边的子三角网,而三点则可构建包含一个三角形或者两条共线边的子三角网。生成子三角网后还需记录最左侧与最右侧的“ghost”三角形,这样两个子三角网拼接时从两个中间的“ghost”三角形开始查找拼接位置。相邻子三角网的拼接以递归方式进行,直至生成最终结果三角网。图 2为两个子三角网A与B的合并过程,AL、AR为A的左、右侧的“ghost”三角形,BL、BR为B的左、右侧的“ghost”三角形。A与B的拼接从AR与BL开始查找,找到合适位置时进行顺序拼接。为了确保拼接后的三角网仍以“ghost”三角网包围,拼接完成后会产生两个新的ghost三角形(图中阴影部分)。AL与BR将用于下次拼接过程,直至整个三角网构网结束。
|
| 图 2 两个子三角网拼接 Fig. 2 Merging of 2 sub-triangulation meshes |
并行分治构网算法在串行分治法基础上进行扩展,将地面脚点在空间上划分为N个点数相等的数据带。对各数据带进行并行构网,结束后会生成N个子三角网,最后对相邻子三角网执行N-1次拼接即可生成整个三角网。
2.3 基于三角网随机分配策略的并行脚点判别算法渐进加密过程中,三角网覆盖了点云数据范围。每个三角形面域在空间范围对应的脚点数反映了该三角形对应的计算量,即落在该面域内部的脚点将首先与该三角形进行判别计算。迭代计算过程中,不同三角形所对应脚点的判别过程不存在依赖关系,可作为计算任务分割的基本单位。三角网中不同三角形的大小不同,对应的计算量也因而存在差异。如建筑密集地带,对应的地面脚点较为稀疏,相应范围内的三角形面积较大,而建筑物稀疏地带对应的地面脚点则相对密集,相应的三角形面积较小。这样,将三角网划分为N个空间范围连续且个数相等的三角形子集合会产生子集合面积差异现象,从而造成计算量差异问题。此外,点云脚点密度还可能存在分布不均匀问题,即使面积相等的不同三角形子集合对应的计算量也可能存在较大差异。因此,三角网的连续划分可能造成不同程度的计算量失衡问题,理想的脚点判别任务划分必须同时兼顾地面脚点的分布差异与点云密度的分布差异。
点云脚点的分布在整体上可能是不均匀的,但在局部小范围可近似认为脚点密度不变。本文引入一种三角网的随机分配方式,通过模运算使每个三角形子集合中的三角形在点云范围内尽可能离散分布。这样,局部范围内计算强度高或者低的相邻三角形被离散划分到不同子集合中,而高密度或低密度的点云分布区域也被离散划分到不同三角形子集合中参与计算,点云分布差异造成的计算量差异从而得到最小化。N个并行处理流程中第n个流程对应的三角形子集合可表达为
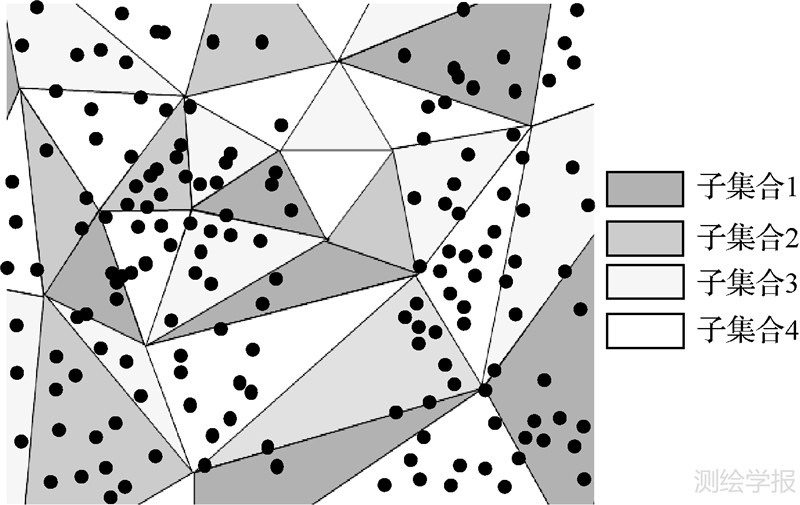
式中,t为三角形编码,mod(t,N)为对t取模运算,模为N。图 3所示为三角网集合随机分配得到的4个三角形子集合,同一子集合中的三角形(具有相同颜色)呈离散分布。其中,第n个子集合内的三角形标识为: T4(n)={t|mod(t,4)=n-1,1≤n≤4}。
|
| 图 3 三角网随机分配 Fig. 3 Random allocation of triangulation mesh |
并行脚点判别的计算时间取决于各流程中计算时间最长的流程,理想效果是各并行流程的计算时间近似相等。为了度量三角网随机分配方式下不同三角形子集合的计算量差异,这里引入平均处理器空闲时间比率来度量并行计算负载均衡情况
式中,Lki为k流程第i次加密滤波时的空闲时间;L为脚点判别总时间;I为加密次数;N为并行流程数;R为平均处理器空闲时间比率。 2.4 并行三角网渐进加密滤波方法渐进加密滤波方法并行化的关键在于2.2节所述的三角网并行构网算法与2.3节的并行脚点判别算法。并行滤波方法以S为输入数据,S′为输出数据,具体步骤描述如下:
(1)生成种子点集合U,对集合S进行二维排序并计算未分类脚点数据集S的矩形范围E,将E按照最大地物尺寸M划分为二维分块序列,选取每个分块内部高程最低脚点形成集合U1,边界范围E的4个顶点作为U2,有U=U1+U2,S=S-U1,地面点数据集S′=U。
(2)构建集合U的三角网T。
(3)并行判别脚点(开始迭代),根据公式(1)将三角网集合T以随机方式划分为N个三角形子集合,有T=∑n=1NTN(n)。N个并行流程进行脚点判别:从TN(n)中取三角形并计算与对应脚点的判别参数值,包括脚点与三角形各顶点的夹角以及脚点到三角形的距离,即参数F(α,β,γ,d),F阈值的确定可参见文献[7]。将满足阈值条件的点集Q加入到S′中,并从S中移除:S′=S′+ Q,S=S-Q。
(4)重构三角网T,如果是首次构网,首先将集合S′平均划分为N个数据带,即S′=∑n=0NS′n,然后N个并行流程构建各S′n的子三角网T′n,依次合并空间相邻的子三角网得到T,如果不是首次构网,则将集合Q中的脚点增量插入到T中。
(5)重复步骤(3)与(4)至最大加密次数I,结束滤波。
在滤波处理中,并行数N可动态调整以确定计算资源的使用比例与算法性能。最大加密次数I可预先设定,一般5~6次可达到较为理想效果。最大地物尺寸M由处理的具体数据决定,对同一数据集串行滤波与并行滤波使用相同的M值。引入M的目的是确定数据网格大小从而进行初始地面种子点的选取,在后续处理中不再直接使用。Axelsson渐进加密滤波方法中F阈值随着加密次数增加而变化,而同一数据集串行滤波与并行滤波在各次迭代过程中F阈值也是相同的。相对于串行方法,并行滤波处理增加了数据划分与结果合并处理,对应增加的计算量可以忽略。F阈值不会影响数据的划分与计算结果的合并,与算法的相对提高效率没有直接关系,暂不纳入研究范围。
3 算法测试及结果分析3.1 试验环境与数据介绍
在计算机架构方面,多核处理器已经成为并行计算的主流模式[17]。并行渐进加密滤波方法的实现需要将点云脚点数据及三角网存储于共享内存中,以便于实现多线程的并发读写。OpenMP(open multi-processing)作为一种主流的共享内存并行编程模型[18],为编写共享内存并行应用程序提供了一套标准的、可移植的API接口[19],适合作为并行加密滤波处理框架。试验选用DELL Precision工作站作为测试平台,CPU配置为Inter(R) Xeon(R)CPU X5550@2.67×8(支持超线程,线程数thr=16);内存:12GB;操作系统:Windows 7×64。
试验选用大连市城区局部范围点云数据(图 4(a)),点数约为1000万,点密度为5.0/m2。该数据分布均匀(图 4(b)),经处理得到正态分布(图 4(c))与集群分布(图 4(d))两种常见分布形态数据。

|
| 图 4 不同空间分布形态点云数据 Fig. 4 Point cloud of different spatial patterns |
试验以加速比(speedup)作为衡量并行渐进加密滤波方法性能的主要指标,文献[20]将其定义为
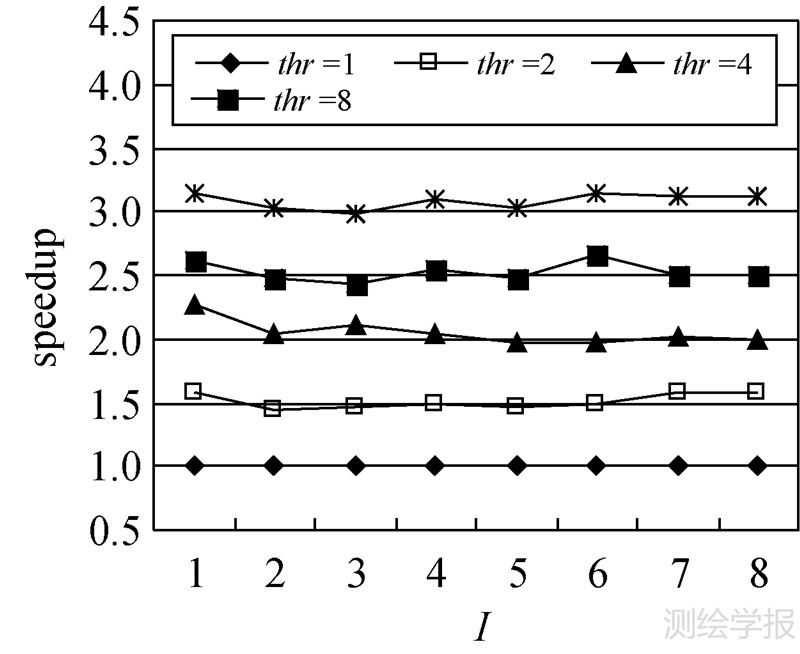
式中,p指处理器核数;Ts指串行滤波算法处理时间;Tp代表p个处理线程并行滤波所需要的时间。加速比反映了并行滤波方法相对于串行方法的效率改进程度。为了测试加密次数对并行方法的影响,试验记录了原始数据在不同并行线程数下多次渐进加密处理时间。由公式(3)计算,得到加速比与加密次数在不同并行线程数下变化关系,如图 5所示。测试结果以串行算法(thr=1)为参照,加密过程中加速比保持不变。随着并行线程数的增加,并行方法的加速比获得稳定增长。在I=2处,各并行测试对应的加速比有略微下降,之后获得较为稳定的比值。加速比下降的原因在于I=2时三角网构建方法由并行到串行的切换,而串行方法所占比例逐渐降低。
|
| 图 5 加速比与加密次数I关系测试 Fig. 5 Test of the relation between speedup and I |
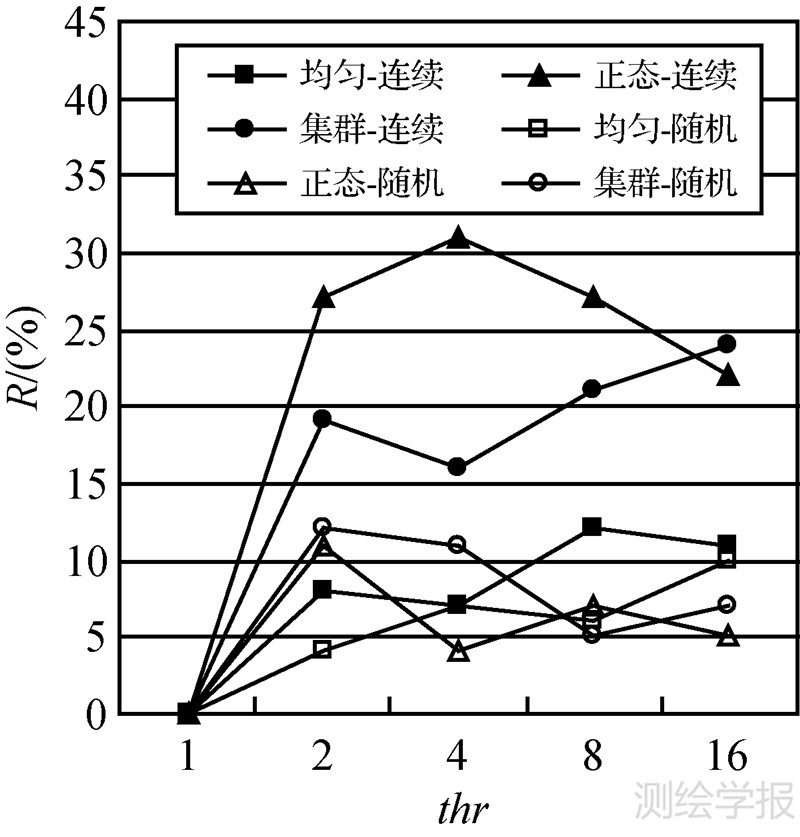
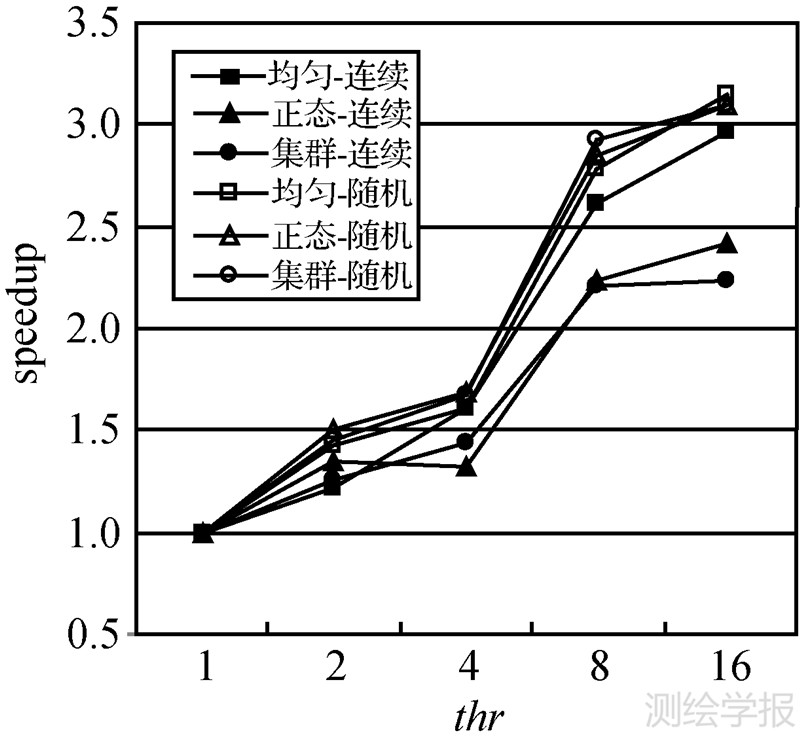
本文引入随机分配策略来解决点云分布差异导致的多线程计算量差异问题。图 6为5次渐进加密滤波处理中,点云数据在连续分配与随机分配两种方式下的平均处理器空闲时间比率R对比,计算方法参见公式(2)。三角网的连续分布与随机分配策略均能较好的适应均匀分布数据。在处理正态分布、集群分布等非均匀分布数据时,连续分配方式下R值较高,且波动较大。而随机分配方式下R值得到有效降低,且波动较小,相应的加速比也较为理想,如图 7所示。
|
| 图 6 连续分配与随机分配R值对比 Fig. 6 Comparison of R in two situations |
|
| 图 7 连续分配与随机分配加速比对比 Fig. 7 Comparison of speedup in two situations |
在加密次数测试中,各加速比曲线相对平稳,各次加密滤波处理均得到较为理想的并行优化。随着并行线程数的增加,加速比值获得显著提高。对于非均匀分布形态数据,连续分配策略会导致较高的平均处理器空闲时间比率,从而影响并行方法的实际性能。随机分配策略下的并行方法能够较好地适应各种分布形态数据,其原因在于的随机分配方式使得计算量高或者低的数据区域被划分到不同数据集,各计算线程被分派的计算量近似相等。
4 结 论本文研究重点在于借助处理器多核计算技术来提高渐进加密滤波方法的实际效率。通过对三角网构网与脚点判别两个最为耗时的计算过程进行并行优化,极大提高了渐进加密滤波方法的实际性能。8核环境下,并行加密滤波方法的加速比约为3.1。1000万左右点云脚点数据的5次加密滤波处理,并行方法仅需要16s左右(不含数据读写时间)。并行加密滤波方法顾及了数据分布形态差异问题,对不同分布形态点云数据具有良好的适应性。从数据角度分析,计算量分布不均是一般滤波方法并行化中普遍存在的问题,论文研究内容为实现复杂场景下串行滤波方法并行改造提供了一种可行的技术思路。为进一步提高算法性能,笔者将进一步研究该滤波方法向处理器计算平台的迁移。
| [1] | AGARWAL P K, ARGE L, DANNER A. From Point Cloud to Grid DEM: A Scalable Approach [C]//Proceedings of 12th International Symposium on Spatial Data Handling. Zurich:[s.n.],2006: 771-788. |
| [2] | HAMMOUDI K,DORNAIKA F, SOHEILIAN B, et al. Extracting Wire-frame Models of Street Facades from 3D Point Clouds and the Corresponding Cadastral Map [J]. Remote Sensing and Spatial Information Sciences, 2010, 38 (3A): 91-96. |
| [3] | ZHANG Xiaohong. Theory and Method of Airborne LiDAR Measurement [M]. Wuhan:Wuhan University Press,2007:9-14. (张小红. 机载激光雷达测量技术理论与方法[M].武汉:武汉大学出版社, 2007:9-14.) |
| [4] | CHEN Q.Airborne LiDAR Data Processing and Information Extraction [J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(2):109-112. |
| [5] | FLOOD M. LiDAR Activities and Research Priorities in the Commercial Sector [J]. International Archives of the Photogrammetry and Remote Sensing, 2001, 34(3): 3-8. |
| [6] | SITHOLE G, VOSSELMAN G. Report: ISPRS Comparison of Filters [R]. Saint-Mandé:ISPRS Commission III Working Group, 2003: 1-29. |
| [7] | AXELSSON P E. DEM Generation from Laser Scanner Data Using Adaptive TIN models [J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2000, 33(B4/1): 110-117. |
| [8] | KRAUS K, PFEIFER N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1998, 53(4): 193-203. |
| [9] | ZHANG K Q. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LiDAR Data [J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4):872-882. |
| [10] | VOSSELMAN G. Slope Based Filtering of Laser Altimetry Data [J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2000, 33 (B3): 935-942. |
| [11] | SITHOLE G. VOSSELMAN G. Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1): 85-101. |
| [12] | HAMMING R W. Digital Filters [M]. 3rd Ed.Hempstead:Prentice Hall International Inc, 1989. |
| [13] | AXELSSON P. Processing of Laser Scanner Data-Algorithms and Applications [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54 (2-3):138-147. |
| [14] | HUANG Xianfeng, LI Hui, WANG Xiao, et al. Filter Algorithms of Airborne LiDAR Data: Review and Prospects [J]. Acta Geodaetica et Cartographica Sinica, 2009,38(5):466-469. (黄先锋, 李卉, 王潇,等. 机载LiDAR数据滤波方法综述[J]. 测绘学报, 2009, 38(5):466-469.) |
| [15] | SU P, DRYSDALE R L. A Comparison of Sequential Delaunay Triangulation Algorithms [C]//Proceedings of the Eleventh Annual Symposium on Computational Geometry.Vancouver: ACM, 1995: 61-70. |
| [16] | SHEWCHUK J R. Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator[C]// Proceedings of the 1st Workshop on Applied Computational Geometry. New York: ACM, 1996. |
| [17] | ASANOVIC K, BODIK R, CATANZARO B C, et al. The Landscape of Parallel Computing Research: A View from Berkeley [R]. Berkeley: University of California, EECS Department, 2006. |
| [18] | DAGUM L, MENON R. OpenMP: An Industry-standard API for Shared-memory Programming [J]. IEEE Computational Science and Engineering, 1998, 5(1):46-55. |
| [19] | CHANDRA R, DAGUM L, KOHR D, et al. Parallel Programming in OpenMP [M]. San Francisco:Morgan Kaufmann, 2000. |
| [20] | SAHNI S,THANVANTRI V. Performance Metrics: Keeping the Focus on Runtime [J]. IEEE Parallel and Distributed Technology, 1996,4(1): 43-56. |