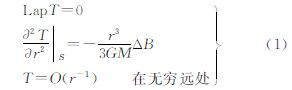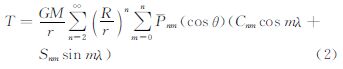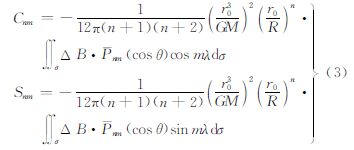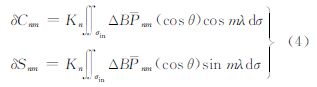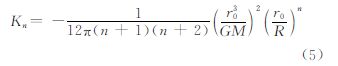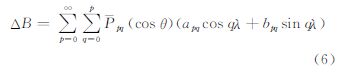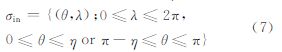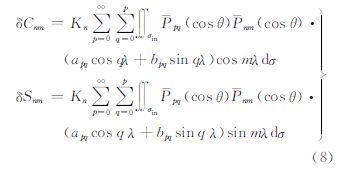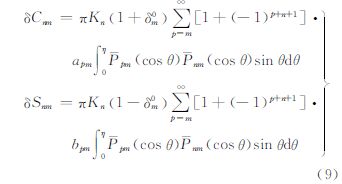2. 中国科学院 研究生院,北京 100049
2. Graduate University of Chinese Academy of Sciences,Beijing 100049,China
1 引 言
GOCE(gravity field and steady-state ocean circulation explorer)[1] 已于2009年3月17日由欧空局发射升空。自发射至今,提供了大量梯度数据。然而由于其轨道被设计成太阳同步轨道,倾角为96.7°,因此在两极有球冠半径约为6.7°的空白区域。随着非极地区域数据越来越密,极地空白对精度提升的影响变得越来越突出。本文将结合具体的解算方法对这种影响进行讨论。从引力场位系数解算的最终方式来看,采用的方法主要包括矩阵解算和积分解算。前者主要是利用最小二乘法或配置算法来进行,而后者则主要利用调和分析来进行。利用最小二乘或配置方法是当前比较流行的GOCE引力场模型解算方法[2],此时极地空白区引起的问题是:对应的法方程组奇异,从而导致解算不稳定,因此通常会采用正则化方法来处理这个问题,常见的有Tikhonov、Kaula正则化方法等[3]。正则化方法会遇到参数如何选取等问题,且主要适用于方程组解算,已有多位学者对此进行了系统讨论,如文献[3, 4, 5, 6, 7, 8]。同时笔者也注意到,文献[9, 10]通过引入Slepian函数讨论了极地空白问题下引力场位系数解算的新方法,较好解决了面球谐函数不正交的问题,但整个过程涉及大量的矩阵计算,计算成本较高。如上所述,此类研究成果已经比较丰富,因此不为本文讨论的重点。
利用调和分析来反解重力场位系数本质上讲是容易实施的,但前提是必须依赖某个确定的边值问题。文献[11]针对引力梯度引入不变量,导出了相应的径向二阶导数边界条件,为调和分析方法应用于GOCE实际数据处理提供了一种新的途径。事实上,文献[12, 13, 14, 15, 16]都对引力梯度不变量进行过研究。相对于矩阵解算,调和分析方法计算量大为降低,但在处理GOCE实际数据时,还须考虑原始数据的低频误差问题和极地的数据缺失问题。针对前者,最有效方法是对原始数据进行滤波,文献[17, 18]均对此进行了讨论,但这些方法大多仅适用于矩阵方法解算GOCE引力场模型。为使得调和分析方法在GOCE数据处理中得以应用,文献[19]引入了“移去恢复”及向前向后双向滤波方法。该方法不仅有效滤除了低频误差,也基本保证了引力梯度数据的正交性未遭破坏,从而使调和分析能够有效地应用到实际GOCE数据处理中。因此极地数据缺失问题成为了调和分析方法应用于GOCE数据中需要重点讨论的问题,尤其是随着非极区数据越来越多,该问题也越来越突出。
本文的主要目的即利用引力梯度不变量的调和分析算法,对GOCE数据处理中的极地空白问题进行讨论。首先简要介绍不变量算法;并在此基础之上,推导出空白区对位系数积分计算的影响公式;最后通过模拟计算来评判空白区问题对重力场恢复的影响和特点。
2 基本原理 2.1 引力梯度不变量算法利用不变量方法解算地球引力场主要基于下列边值问题[11, 20]
式中,Lap是Laplace算子;T=v-V是扰动位;v是地球引力位;V是参考引力位;S是卫星轨道平均球面(半径记为r0);GM是地球质量万有引力常数;ΔB=B-B0是不变量扰动;B和B0分别对应于v和V的梯度不变量[10]。在问题(1)中B由观测数据得到,而B0则用参考引力位计算所得,从而ΔB已知,因此若将扰动位T表达成下列球谐级数。 则系数可利用问题(1)解得 式中,R是地球的平均半径;Pnm(cosθ)是规范化的n阶m次连带Legendre函数;θ、λ分别是余纬和经度;σ是单位球面;dσ是积分面元。从式(3)可知,若利用不变量方法从GOCE数据恢复地球引力场,其最终的计算形式归结为积分计算,避免了大型方程组的解算难题。但是公式(3)中的积分区域是整个球面,而实际GOCE的轨道存在着观测空白区,因此必须估算出该空白区对积分的影响。
2.2 观测空白区对引力场恢复的影响分析观测空白区问题对不同的反演方法所产生影响的途径不同。对于最小二乘算法,其影响是相应矩阵求逆不稳定,从而在解算过程中需引入正则化方法;对于调和分析方法,其影响则是积分计算的精度损失。为了叙述方便,将公式(3)中的积分区域σ划分成内区(观测空白区域) σin和外区σout,显然在外区σout上ΔB有观测值,而在内区σin上不存在观测值。
针对内区σin观测数据的缺失问题,可采用“移去恢复法”解决,即利用某个已知的引力场模型的模拟值在σin上去替代观测值。若参考引力场也选为该模型,可以证明此时扰动位的位系数计算误差为
式中 是仅与阶数n相关的常数。由此可见,观测空白区对位系数恢复主要受空白区域大小与参考引力位选择的影响。具体到GOCE,观测空白区是地球两极附近角半径约为6.7°的球帽,其面积仅为整个地球表面的0.68%左右,尽管所占比例不大,但这并不意味着极区空白可忽略,下节将通过数值模拟予以说明;而对于参考引力位,显然选择精度越高的参考引力场模型将会使得ΔB越小,从而对计算的位系数的精度损失就越小。
为了便于讨论,将ΔB展开成如下球谐级数
式中,apq和bpq是ΔB的球谐系数,另外内区σin可以近似表示成南北两极角半径为η的球帽,即 直接将式(6)代入公式(4)中,可得 对式(8)进行化简,可得 公式(9)便是ΔB缺失σin中数据后对扰动位的位系数计算产生的影响,其中δ0m为Kronecker符号。由该式可知,该影响项几乎涵盖了ΔB的球谐展开中不同阶的项。对系数apq和bpq而言,通常阶数p越小其值越大,从而对系数误差的影响就越大,即:总体而言低阶项将在空白区的影响中占主要因素。为了具体分析其特点,将通过数值模拟来进行讨论。 3 数值模拟与精度分析 3.1 空白区域大小的影响
此部分主要结合问题(1)给出的算法,对空白区大小的影响进行讨论。首先取GOCE轨道的平均球面半径r0=6633.037km,用EGM08模型的前300阶在轨道平均球面S上模拟出地方指北坐标系下的梯度六分量作为观测值,同时用EGM96模型的前300阶作为参考引力位,进行类似数值模拟;然后在S上按20′×20′格网分别计算相应的不变量扰动,并表示出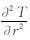 ,从而反演出位系数。最终的误差评定从与EGM08的对比中得到。为了显示极区大小的影响,图 1给出了无极区空白和极区空白区域σin大小依次为1°、3°、6.7°、10°、15°时的误差阶方差[21]。
,从而反演出位系数。最终的误差评定从与EGM08的对比中得到。为了显示极区大小的影响,图 1给出了无极区空白和极区空白区域σin大小依次为1°、3°、6.7°、10°、15°时的误差阶方差[21]。
|
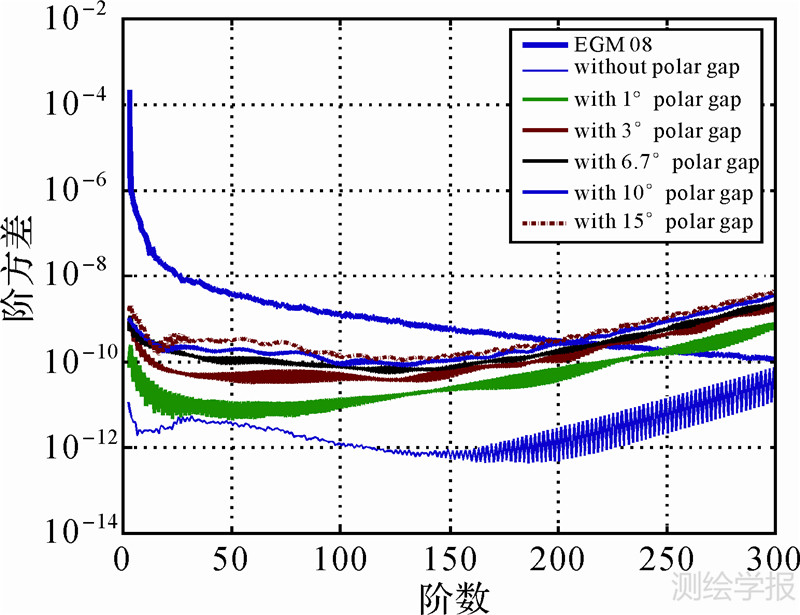
| 图 1 模拟计算结果的阶方差图 Fig. 1 Degree variance |
由该图易知,若不存在空白区的影响,对式(1)给出的边界条件进行调和分析可以保证引力场反演的精度;同时也不难看出,极区虽小,但对位系数整体精度影响较大,例如相对无空白区情况,极区空白1°几乎将精度降低一个量级;随着极区空白区域的增大,误差阶方差逐渐变大,且变化率逐渐减弱,例如:空白区从10°到15°时的精度变化不如1°到3°明显。
由于阶方差反映的是各阶的平均误差,难以反映不同次之间的差别,所以下面进一步地给出上述结果的相对误差图(取以10为底的对数),即分阶次反映位系数恢复的精度。
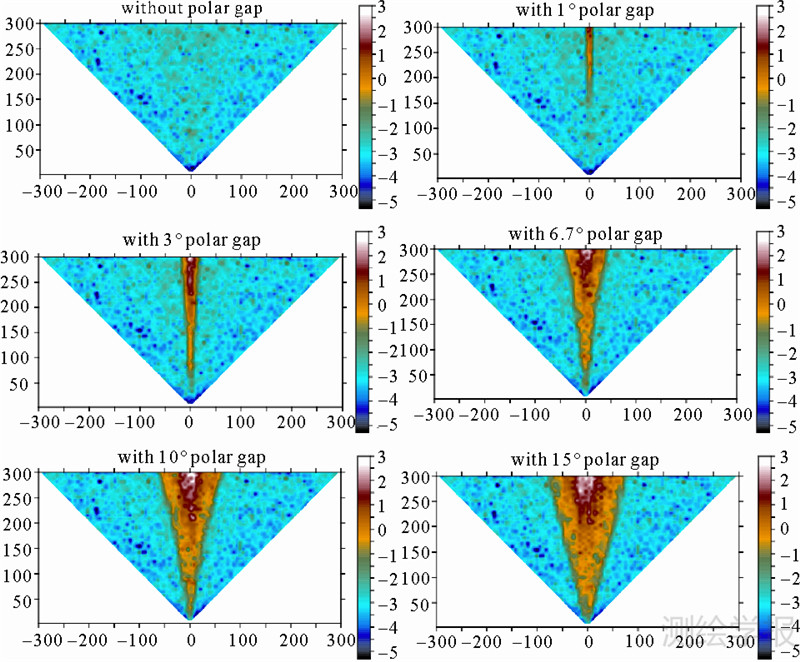
从图 2可以明显看出,极区空白主要影响引力场同阶项中的低次部分,受影响的阶次呈三角状,且阶和次基本满足下式[22]
|
| 图 2 相对误差 Fig. 2 Relative error |
式中,n为阶;m为该阶受影响的最大次;θ为极区空白的球冠半径(用弧度表示)。这种特点产生的原因为:低次项系数一般大于同阶中高次项,同时由公式(9)可知,极地空白引起的位系数误差按次传递,即主要在具有相同次的位系数之间累积,低次位系数由于求和中的项数多且量级大,所以误差积累将更快,这就导致了低次项位系数的误差比同阶中其他次的量级要大[23]。 3.2 不同参考引力位的影响
此节主要讨论不同参考引力位对整体精度的影响。观测值仍采用上节EGM08模型给出的模拟值;而将EGM96、EIGEN-5C模型的前300阶分别作为参考引力位进行讨论。其中,EIGEN-5C是由德国地学中心(GFZ)和法国空间大地测量研究小组(GRGS)利用多年GRACE数据并结合其他数据反演得到的静态引力场模型,由于C20精度较差,计算时将其换为EGM08模型C20。分别删除极区6.7°的观测值后,进行调和分析并进行迭代计算。结果如图 3。
|
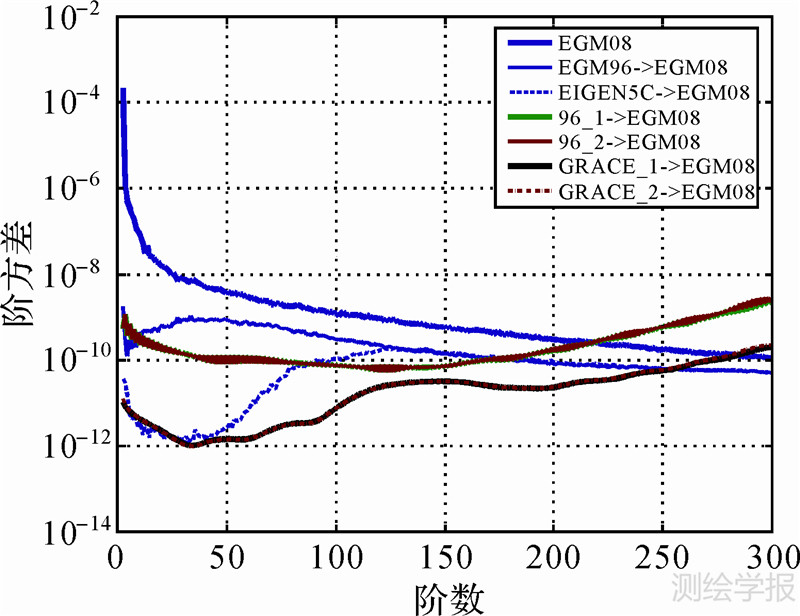
| 图 3 阶方差 Fig. 3 Degree variance |
图 3给出了各个计算模型相对EGM08的阶方差。其中96_1、GRACE_1分别表示利用EGM96、EIGEN5模型当参考引力场模型的解,96_2、GRACE_2则表示分别用新模型96_1、GRACE_1作参考引力位迭代计算一次的解。不难发现,参考引力位越精确,误差阶方差越小;同时从EIGEN5和EGM96的对比也可看出,参考引力场低阶位系数的精度对最终模型的整体精度影响较大。不仅低阶项精度差异明显,高阶同样如此。原因在于,极地数据的缺失,球谐函数的正交性受到了破坏,各阶之间将会相互影响。这从公式(8)和(9)中可以得到证明。同时也不难得出,迭代对整体精度的提升效果不明显。这主要是因为极区信号严重依赖于先验模型,迭代时,相当于用新的模型模拟极区观测值,然而新模型的低次仍然主要依赖于起初的先验模型。
提供空间分辨率为100km的厘米级大地水准面是GOCE卫星发射的主要目的之一[1]。下面将通过96_1、GRACE_1前200阶(对应的空间分辨率为100km)所计算的大地水准面的精度对比,来讨论分析不同参考模型的影响,结果如图 4所示。
|
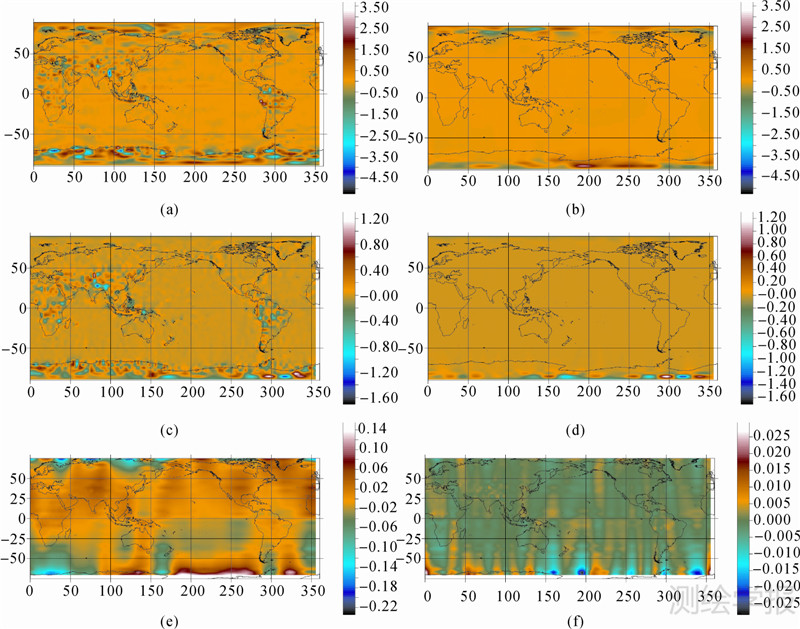
| 图 4 大地水准面误差 Fig. 4 Geoid error (unit:m) |
图 4中,(a)、(b)分别表示EGM96及模型96_1与EGM08所计算的大地水准面的差异;(c)、(d)则表示EIGEN-5C及模型GRACE_1与EGM08所计算的大地水准面的差异。由于两极和非极区量级差异较大,为了突出非极区,(e)、(f)仅显示了(b)、(d)南北纬75°之间的区域。从 图中容易看出,利用EIGEN-5C作参考引力位时反演精度更高,这说明先验模型对最终模型的整体精度有较大影响。从区域来看,非极区大地水准面的精度明显高于两极。例如:在非极区,如南北纬50°之间的区域,(e)、(f)所示大地水准面的差异大约分别位于10cm和1cm以内,而(a)、(c)最高可达米级;但在极区,(b)、(d)所示的最大差异可达米级,量级和(a)、(c)一致。这表明:非极区更主要体现观测值的信息(此试验为EGM08),而极地空白区则更主要体现先验模型的信息(此试验为EGM96和EIGEN-5C)。
4 结 论本文结合不变量方法,推导了两极空白区对利用GOCE数据恢复引力场的影响公式,并通过数值模拟,详细讨论了极地空白问题对引力场恢复的影响。
由于正交性遭到破坏,所以极区空白不可忽略,且主要影响低次部分。此外在极区空白大小确定的情况下,受影响的阶和次满足一定的近似线性关系。精度高的参考引力场模型能够减弱极地空白带来的精度损失,其途径就是使用“移去恢复法”,相当于在空白区用参考引力场数据代替观测值;虽然最终反演模型的整体精度将在一定程度上受制于参考引力场模型,但在远离两极的地区,大地水准面精度却主要受观测值影响,参考模型更主要影响极区大地水准面的精度。
虽然本文采用不变量方法进行反演,但上述结论仍适用于其他方法。为了减弱极地数据缺失所引起的精度损失,若采用“移去恢复法”,需选用高精度的参考引力场模型;若采用正则化方法,应考虑添加精度高的约束条件。由于极地问题对地球物理研究意义重大,且随着GOCE非极区数据的日益增多,对极区问题的研究和处理方法需要作进一步探讨,例如可考虑结合地面或其他观测数据类型,构建超定边值问题来进行讨论[24]。
| [1] | BALMINO G, RUMMEL R, VISSER P, et al. The Four Candidate Earth Explorer Core Missions: Gravity Field and Steady-State Ocean Circulation Mission[R]. Noordwijk: ESA Publications Division, 1999. |
| [2] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819-843. |
| [3] | SNEEUW N, GELDEREN M V. The Polar Gap[J]. Lecture Notes in Earth Sciences, 1997, 65:559-568. |
| [4] | KUSCHE J, KLEES R. Regularization of Gravity Field Estimation from Satellite Gravity Gradients[J]. Journal of Geodesy, 2002, 76(6-7): 359-368. |
| [5] | KOCH K R, KUSCHE J. Regularization of Geopotential Determination from Satellite Data by Variance Components[J]. Journal of Geodesy, 2002, 76(5): 259-268. |
| [6] | METZLER B, PAIL R. GOCE Data Processing: The Spherical Cap Regularization Approach[J]. Studia Geophysica et Geodaetica, 2005, 49(4): 441-462. |
| [7] | XU Xinyu, LI Jiancheng, WANG Zhengtao, et al. The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 465-470. (徐新禹,李建成,王正涛,等. Tikhonov正则化方法在GOCE重力场求解中的模拟研究 [J]. 测绘学报, 2010, 39(5): 465-470.) |
| [8] | XU Xinyu. Study of Determining the Earth’s Gravity Field from Satellite Gravity Gradient and Satellite-to-satellite Tracking Data[D]. Wuhan: Wuhan University, 2008. (徐新禹. 卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究[D]. 武汉:武汉大学, 2008.) |
| [9] | ALBERTELLA A, SANSO F, SNEEUW N. Band-limited Functions on a Bounded Spherical Domain: The Slepian Problem on the Sphere[J]. Journal of Geodesy, 1999, 73(9): 436-447. |
| [10] | ZHU Guangbin, LI Jiancheng, WEN Hanjiang, et al. Slepian Localized Spectral Analysis of the Determination of the Earth’s Gravity Field Using Satellite Gravity Gradiometry Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 1-7. (朱广彬,李建成,文汉江,等. 卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法[J]. 测绘学报,2012, 41(1): 1-7.) |
| [11] | YU Jinhai, ZHAO Dongming. The Gravitational Gradient Tensor’s Invariants and the Related Boundary Conditions[J]. Science in China: Series D: Earth Sciences, 2010, 53:781-790. (于锦海,赵东明. 引力梯度不变量与相关边界条件[J]. 中国科学: 地球科学, 2010, 53(5): 781-790.) |
| [12] | RUMMEL R. Satellite Gradiometry[J]. Lecture Notes in Earth Sciences, 1986, 22: 317-363. |
| [13] | HOLOTA P. Boundary Value Problems and Invariants of the Gravitational Tensor in Satellite Gradiometry[J]. Lecture Notes in Earth Sciences, 1989, 25: 447-457. |
| [14] | SACERDOTE F, SANSO F. Some Problems Related to Satellite Gradiometry[J]. Bulletin Géodésique, 1989, 63(4): 405-415. |
| [15] | VERMEER M. Observable Quantities in Satellite Gradiometry[J]. Journal of Geodesy, 1990, 64(4): 347-361. |
| [16] | BAUR O, SNEEUW N, GRAFAREND E W. Methodology and Use of Tensor Invariants for Satellite Gravity Gradiometry[J]. Journal of Geodesy, 2008, 82(4-5): 279-293. |
| [17] | SCHUH W D. The Processing of Band-limited Measurements: Filtering Techniques in the Least Squares Context and in the Presence of Data Gaps[J]. Space Science Reviews, 2003, 108(1-2): 67-78. |
| [18] | REGUZZONI M, TSELFES N. Optimal Multi-step Collocation: Application to the Space-wise Approach for GOCE Data Analysis[J]. Journal of Geodesy, 2009, 83(1): 13-29. |
| [19] | YU Jinhai, WAN Xiaoyun. The Frequency Analysis of Gravity Gradients and the Methods of Filtering Processing[C]// Proceedings of 4th International GOCE User Workshop. Munich: ESA: 2011.) |
| [20] | YU Jinhai, WAN Xiaoyun. Recovery of the Gravity Field from GOCE Data by Using the Invariants of Gradient Tensor[J]. Science in China: Series D: Earth Sciences, 2012, 42(9): 1450-1458. (于锦海,万晓云. 利用引力梯度不变量解算的GOCE引力场模型[J]. 中国科学: 地球科学, 2012, 42(9): 1450-1458.) |
| [21] | YU Jinhai, WAN Xiaoyun. Reduction for Gradiometry and Corresponding Imitation[J]. Chinese Journal of Geophysics, 2011, 54(5): 1182-1186. (于锦海,万晓云. 引力梯度归算的模拟计算[J]. 地球物理学报,2011, 54(5): 1182-1186.) |
| [22] | GELDEREN M, KOOP R. The Use of Degree Variances in Satellite Gradiometry[J]. Journal of Geodesy, 1997, 71(6): 337-343. |
| [23] | ZHONG Bo. Study on the Determination of the Earth′s Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan: Wuhan University, 2010. (钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉: 武汉大学, 2010.) |
| [24] | YU Jinhai, PENG Fuqing. Variational Solution about Over-determined Geodetic Boundary Value Problem and Its Related Theories[J]. Science in China: Series D: Earth Sciences, 2007, 37(1): 39-45. (于锦海,彭富清. 超定大地边值问题的变分解及相关理论[J]. 中国科学: 地球科学,2007, 37(1): 39-45.) |