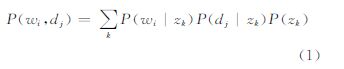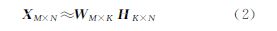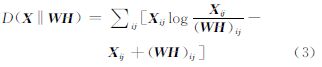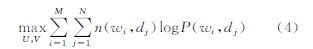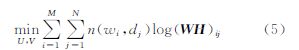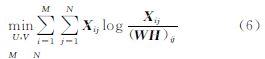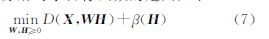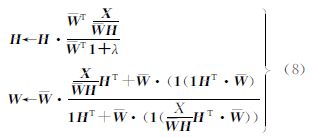2. 上海师范大学 城市信息研究中心,上海 200234
2.Urban Information Research Center,Shanghai Normal University,Shanghai 200234,China
1 引 言
高光谱影像具有丰富的波段，可用于识别光谱吸收特征较窄的物质，比传统的多光谱遥感图像蕴藏更为丰富的信息。高光谱影像作为一种高维数据所呈现出的“稀疏性”和空空间现象正是维度灾难的具体表现,这就使得传统分类方法受限，影响了分类精度，也使得处理过程中的计算量巨增。因此寻找高维数据的合理子空间，并在相应子空间中研究数据的特性，是减小“维度灾难”影响的一个有效途径。不同于特征提取算法，波段选择是基于原始数据上的降维，而非变换域上的变化，降维后形成新的高光谱影像空间在不损失重要信息的条件下可充分代表其他波段信息，并且其结果更便于处理和解译。
近年来，有关高光谱图像波段选择的研究不断增多。可依据Jeffries-Matusita距离、 离散度或Bhattacharya距离为区分准则，通过先验目标信息进行监督式的波段选择。但先验信息往往难以获取，非监督的波段选择成为主要研究的内容，如：基于波段排序思想，采用信息散度(information divergence,ID)[1]或最大方差主成分分析(maximum-variance PCA，MVPCA)的波段选择方法[2]；把高光谱影像目标检测领域的约束能量最小化(constrained energy minimization,CEM)应用到波段选择[3]；抑或将波段选择视做一种数据聚类过程，应用非监督聚类法进行波段选择[4, 5, 6]。
上述这些方法多侧重于对波段信息量和相关性的研究，但少从高光谱数据内在特征(如：非负性和稀疏性)来考虑各个波段数据中地物之间的光谱差异性。事实上，高光谱遥感记录了地物电磁波谱特性，由此反映地物光谱能量信息，因此不可能存在负值，其自身具有非负特性；从高光谱影像的像素空间来看，混合像元只是几种端元的叠加，端元的丰度分布一般都不会充满整个图像空间，且混合能量的大小是限定的，也不可能无限大，因此高光谱影像端元分布具有稀疏性。高光谱在光谱域上的密集采样易造成数据的冗余，使其具有高维数据的稀疏性；同时从小波理论的角度来看，由小波变换的线性变换可知，自然图像在小波域上通常可以进行稀疏表示，即变换前后保持的是小波系数的能量。高光谱影像存在的空空间现象意味着空间的多变量数据通常在低维拓扑结构中，高维数据的线性投影还表现出多正态分布组合的特性[7]，所以当高光谱数据投影到低维子空间时并不会丢失重要信息，仍可表达地物光谱的差异。
本文就基于高光谱影像的非负性和稀疏性特点，进一步应用稀疏非负矩阵分解良好的聚类特性，将其作为线性子空间分析技术实现高光谱影像波段有效选择。
2 基于非负矩阵分解的高光谱波段聚类 2.1 高光谱波段聚类聚类分析作为一种非监督方法，可在样本或者地面真实值未知的情况下，通过聚类抽取特征向量进行波段选择。常见的有：应用k-means的波段选择[4]；使用互信息层次聚类方法进行波段聚类[5]和基于仿射传播(affinity propagation，AP)非监督聚类的波段选择[6]。然而基于低维空间距离函数的k-means聚类算法在选择聚类中心时使用简单平均的方法，不能区分含有不同信息量的不同波段的重要性差异。对于层次聚类，聚类迭代的阈值选择则成为聚类的一个关键。仿射传播聚类尚有两个未解决的问题：一是偏向参数取值对最优聚类结果的影响；另一是当震荡发生后算法不能自动消除震荡并收敛。因此本文引入文本分析中的概率潜在语义分析模型将目标表述为潜在成分的概率组合,然后利用统计模式识别方法对获取的潜在成分概率进行判别，从而完成波段聚类。
概率潜在语义分析(probabilistic latent semantic analysis，PLSA)通过使用两个矩阵的乘积逼近样本出现的概率矩阵，使得这两个矩阵具有概率意义，并将文档由单词空间映射至主题空间，由此来完成文档聚类进而从语料库中发现隐含的语义信息[8]。即在观测到的文档-单词共现矩阵(w,d)对，其中主题变量z是隐含的而且未被观测到的。假设文档d和单词w在给定的主题z下条件独立，其概率公式为
并根据P(dj|zk)可以判定文档类别为zl=argmax{P(di|z1),P(di|z2),…,P(di|zk)},从而完成聚类。
PLSA主要用于文本主题建模，但随着其应用的推广，PLSA已被应用到高分辨率遥感影像的信息提中[9]和高光谱像元的聚类中[10]。因此从空间域的像元聚类转换到光谱域的波段聚类，把高光谱影像中的波段看成待分析文本集中的文档(d)，将波段所属类别看做文本主题(z)，而每个波段中所地物类型分布即为文本中的单词(w),其中，P(dj|zk)代表波段j属于第k个类别的概率；而P(wi|zk)则为像素i所属类别的概率。利用PLSA方法较强的鉴别能力对各波段进行分析,找出其最可能属于的类别,从而完成高光谱影像波段聚类。
尽管PLSA能给分解结果很好的概率解释，然而波段选择作为子空间分析方法是通过高光谱影像波段聚类获取光谱局部有效特征，且PLSA算法本身存在的过拟合以及无法提取局部特征的问题。因此希望利用求解过程的等价性，将基于概率的特征抽取算法视做一种加了归一化限制的非负矩阵分解算法，从而选择局部有效特征。
2.2 非负矩阵分解的波段聚类特性非负矩阵分解(nonnegative matrix factorization,NMF)以非负约束将原始矩阵分解成左右两个非负矩阵，并以基向量组合的表示形式，具有很直观的语义解释，可反映人类思维中“局部构成整体”的概念[11]。假设处理高维数据XM×N，该数据矩阵中各个元素都是非负的,表示为X≥0 对矩阵XM×N进行线性分解,有
式中，K小于M和N。X的每个样本可以近似看做基矩阵W的列向量的非负线性组合，组合系数就是H的行分量。由此表明，如果能寻找到合适的基向量组，使其能够代表数据之间潜在的结构关系，就可以用少量的基向量组来表征大量的数据向量，并会获得很好的逼近与表示效果。
NMF应用目标函数D(X,WH)来保证逼近效果，通常目标函数可以由欧式距离或K-L散度来表示。从目标函数和特征向量的选取范围可知，当NMF目标函数中基矩阵W的各列向量的取值范围被限制为一个仅包含2n个元素的样本中心向量集合,并且系数矩阵H中各列向量取值被限制为单位基向量时,以欧式距离目标函数的NMF 算法简化后就退化为k-means聚类[12]，利用这种等价关系，文献[13]进行了高光谱波段选择。但是只有在随机误差为高斯分布时，基于欧氏距离的最小二乘才能使目标函数最优，而高光谱影像波段自身并非高斯分布，因此本文选用K-L散度为目标函数。K-L散度作为距离的概率测度，对噪声不是很敏感，鲁棒性更强，更适合处理随机信号，其表达式为
基于散度目标函数的NMF虽然与PLSA模型构造不同，但是它的求解过程却和NMF很相似，如下进一步证明PLSA等价于对W、H进行归一化限制后的一种NMF算法变体[14]。
包含隐含变量的PLSA可通过最大期望算法(expectation maximinization，EM)来求解P(dj|zk)和P(wi|zk)，其目标函数为使得最大似然估计达到最大
构造矩阵W和H，使得W=P(wi|zk)P(zk),H= P(dj|zk)，则式(4)中的目标函数可简化为：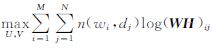
，可等价于
NMF中以K-L散度作为目标函数，并对NMF中W、H进行归一化，使得X=WH=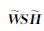
,其中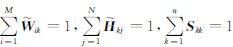
,由此使得NMF的目标函数由式(3)变为
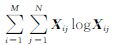为常数，则NMF与PLSA是等价的。
这种NMF变体的归一化限制不仅使得PLSA的分解结果更具概率意义，而且使得传统的EM方法也成了一种特殊矩阵的分解方法，由此NMF作为特征抽取的方法具备良好的聚类特性，可应用于高光谱影像的波段聚类，并从聚类的波段中选择出最大信息量的波段作为波段选择的结果。
3 应用稀疏非负矩阵分解聚类的高光谱波段选择算法 3.1 稀疏非负矩阵分解求解稀疏表示对于高维数据而言是一种有效的表示方法,同时基于局部表达能力的NMF算法本身也是一种稀疏表示,NMF可聚类的特性也是一种稀疏处理。但是基本NMF算法的稀疏能力和程度是比较弱和难以控制的，需要利用稀疏约束来加以控制。稀疏性还与NMF分解的唯一性有着非常密切的联系，是不可分性和分解唯一性的必要条件。因此作为非负矩阵分解的拓展，稀疏非负矩阵分解对于目标函数的定义如下[15]
式中，β作为NMF惩罚项的稀疏度，可以用l0范数，但这会造成NP问题。为了简化算法，文献[16]提出了简化的β(H)=λ∑i,jHi,j来做稀疏惩罚项，λ用来权衡稀疏度和逼近精度，且λ>0，稀疏度λ越大向量取值就越稀疏。
D(X‖WH)对于单独的W或H而言，都是凸函数，但是同时对W和H而言，却都不是凸函数，如此要找到全局最优解是不现实的。因此，基于K-L散度的稀疏非负矩阵分解的W和H采用迭代规则，保证在W和H非负的前提下，找到局部最优，其表达为[16]
式中，W是基矩阵的列向量归一，1是一个与矩阵相对应的全1方阵。
通常在分解过程中，对变量W和H普遍采取随机初始化模式,但随机初始化模式易使得同一实验条件下的处理结果和时间开销较大差异,只有进行多次NMF仿真运算取平均值作为最终结果,这显然大大降低了算法的运行效率和实时性。由此采用NNDSVD[17]的方法进行初始化，使得在有限的迭代步数内，NMF模型能更快地收敛。
3.2 SNMF-BS算法流程鉴于高光谱影像的高维、非负、稀疏特点，且基于K-L散度的NMF与PLSA聚类等价，本文构建稀疏非负矩阵分解聚类的高光谱波段选择算法(sparse NMF band selection，SNMF-BS)流程(图 1)，即：
|
| 图 1 上海PHI的高光谱近红外假彩色影像 Fig. 1 PHI-3 experimental data |
高光谱影像R∈RM×N×L，其中L为光谱维，M×N为影像的像素空间，为了便于计算，将三维立方体结构转变成二维结构，即X∈RP×L，其中P=M×N。
对于二维结构的高光谱，在波段选择的过程中，首先需要确定波段选择数量。由于高光谱影像的谱向特征无法用已经确知的特征来定义，且干扰信号的出现影响了数据维数的确定，所以针对目标检测与分类应用方向，虚拟维数(virtual dimensionality，VD)[18]依据数据中的可分谱向特征数目对数据维数进行界定，应用基于纽曼一皮尔逊准则的HFC方法计算波段选择数量。为了进一步降低噪声对虚拟维数的影响，首先应用相邻波段的相关性去除受水汽影响大的波段和低信噪比的波段；其次对去除水汽和低信噪比的波段采用噪声白化处理，消除了HFC之前信号的二阶统计相关性。由此拟定相关特征值和协方差特征值的比较阈值，可得到波段选择数量K。
接着采用稀疏非负矩阵分解进行波段聚类，即XP×L≈WP×K HK×L，其中K为通过虚拟维数确定的波段选择数量(波段聚类数)。为了保证算法的通用性，在不失一般性的情况，将NMF模型∑i,jXi,j =1，否则W和H会被缩放。通过非负双重奇异值分解进行初始化，依据以K-L散度为目标函数的稀疏非负矩阵分解的W和H迭代规则，最终得到可表征每个波段影像数据X(l,.)可由基矩阵W和系数矩阵H的线性组合。
根据NMF与PLSA等价性准则，同时引入A、B两个k阶对角线缩放矩阵，即Akk=∑iWik,Bkk=∑jHkj。NMF可改写为
式中，W=WA－1等价于P(wi|zk)，H=B－1H等价于P(dj|zk)，S=AB等价于P(zk)。
最后由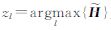
来完成高光谱影像波段聚类，聚类中类别里的最大值band_selection=
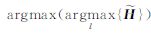则为所要选择的波段。
稀疏非负矩阵分解的波段选择(SNMF-BS) 算法流程如下。
输入：高光谱影像，稀疏度。
输出：特征选择的波段号。
步骤：
(1)高光谱三维立方体转二维表达。
(2)数据预处理：去除水汽波段；去除低信噪比波段； 数据白化。
(3)应用虚拟维数确定波段选择数量。
(4)通过NNDSVD初始化SNMF，并由SNMF获取稀疏系数矩阵H。
(5)根据NMF与PLSA等价性准则，通过W、H的归一化完成高光谱影像波段聚类。
(6)选择聚类中类别里的最大值，则为所要选择的波段号。
3.3 SNMF-BS波段选择算法评价为了研究稀疏NMF聚类算法自身对高光谱影像波段选择的效用，本文将特征有效性的量度准则引入波段选择评价中,并对波段子集的信息量、相关性和可分性进行分析评价。
首先对波段聚类的有效性进行分析。通过基于类内散度与聚类中心间距的Davies-Bouldin(DB)指标来评定类间的可分性，DB越小表示类与类之间的相似度越低，聚类效果越佳；Krzanowski-Lai(KL)指标用类内离差矩阵作为测度，值越小表明类内越紧密；Calinski-Harabasz(CH)指标则是由分离度与紧密度的比值得到，CH越大代表着类自身越紧密，类与类之间越分散，有更优的聚类结果[19]。
由于稀疏非负矩阵分解是采用线性组合的方法，基于此方法的波段子集数据m特征值与原始波段n间有一定比例关系，所以从数据压缩意义角度，在尽量减少原有数据有用信息损失的条件下,用相对少的部分特征有效地表现原始特征。在此选用文献[20]提出的KLC评估标准[20]，即将波段子集数据的主成分分析特征值总和除以原始的波段数据主成分分析的特征值总和的n分之m作为所选波段子集信息量的评估标准，从信息量角度进行波段选择度量。理论上,KLC的值应在1左右浮动。其值大于1,说明所选波段的信息量优于其他波段；小于1则表示所选波段的信息量不比其他波段多。
波段间的相关性反映了不同波段间信息的冗余度,在相同的条件下,弱相关性对应着更多的信息量，因此应用波段子集间的相关性均值来度量，相关性值越小则冗余度较小。
除信息量和相关性度量外，所选特征能更有效地描述地物类别也是评价波段选择的关键。鉴于非负矩阵分解可进行双向聚类，且在概率潜语义分析聚类模型中P(wi|zk)则为像素i所属类别的概率可在像素空间进行聚类，因此采用silhouette(S)指标通过计算类间的聚类及类内的距离来衡量波段选择下像素空间聚类的可分性，S越大则可分性越强[19]。
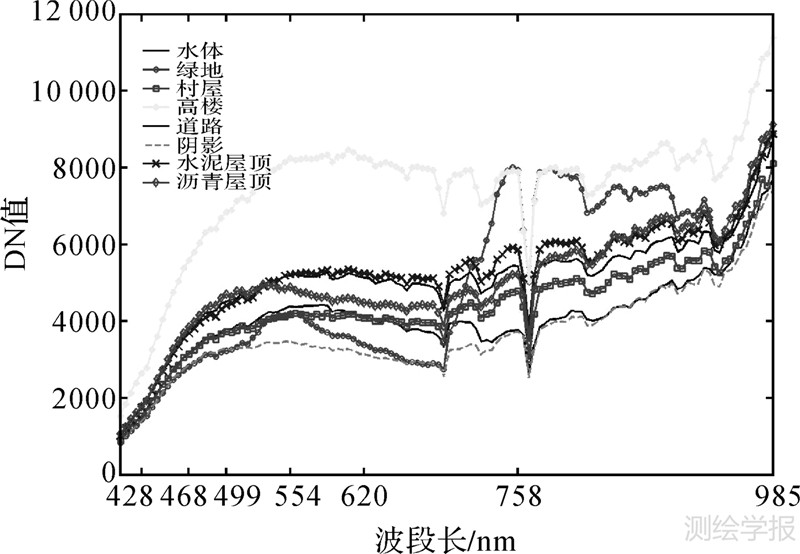
4 试验分析 4.1 试验数据2003年10月获取的124个波段的PHI-3机载高光谱数据，其工作波长为408～985nm：紫色1～5波段(408.95～428.55nm),蓝色6～14波段(432.95～468.25nm),青色15～21波段(472.65～499.05nm),绿色22～33波段(503.65～554.65nm),橙色34～47波段(559.25～620.00nm),红色48～76波段(624.80～758.40nm),近红外77～124波段(763.15～985.25nm)；光谱分辨率为4～5nm；地面分辨率2.4m×2.4m；瞬时视场为0.6mrad；数据量化率为12bit。所选试验区域范围为上海市浦东新区龙阳路—大严家湾—小严家地区，如图 1所示，具有368扫描行数据，每行有396个像元。影像中包含的地物信息多样复杂，有水体、绿地、高楼，普通居民用地和道路等，如图 2所示。整幅影像的各波段间相关性和协方差分析如图 3。 协方差越大,图中颜色越浅。
|
| 图 2 PHI高光谱影像中主要地物光谱值信息 Fig. 2 Spectrum of different objects in PHI imagery |
|
| 图 3 PHI高光谱影像各波段间的相关性及协方差 Fig. 3 PHI-3 imagery bands correlation and covariance |
依据SNMF-BS算法流程，通过相邻波段的相关性比较法去除高光谱影像中受水汽影响大的波段和低信噪比的波段，PHI数据剩余波段数为110。对于剩余波段，经过噪声白化处理后，根据不同的比较阈值[10-3,10-4,10-5,10-6,10-7],由HFC虚拟维数确定上海PHI数据的波段选择数量分别为[11, 7, 5, 5, 3]。
波段选择数量即聚类个数，采用改进的稀疏非负矩阵分解法对剩余波段数据进行分解，依据NMF与PLSA等价性准则，得到相应数量的波段聚类，并在系数矩阵中提取每个聚类的最大值作为所要选择的特征波段,整个过程是非监督的。因此波段选择结果见表 1，反映了尽管由于人为因素的介入，地物受环境的影响因素复杂，表现为各种地物凌乱的交错分布，但就整体而言大部分地物的能量信息集中在绿、红、近红外这3个波段组中，即550～922nm，这其中的波段选择可以使得波段间相关性较小且所包含的信息量较大。
| 波段数 | 波段号 |
| 11 | 33,43,54,59,62,67,73,77,79,108,110 |
| 7 | 32,54,62,67,77,81,111 |
| 5 | 32,44,62,75,111 |
| 3 | 67,81,111 |
该算法是无用户定义的优化参数，对编码稀疏度高，可使目标函数单调下降，其迭代性能稳定。但作为一种稀疏编码，还需关注H的行的稀疏性，因此根据文献[21]中对NMF算法稀疏性度量公式sparseness(x)，对H的稀疏度度量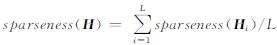
，得到不同稀疏性调节因子λ下SMNF稀疏度的情况，见表 2。 由此发现，当稀疏度参数λ＞0.1时，稀疏非负矩阵分解的向量表示得非常稀疏这与影像中反映的同一类型地物的光谱响应零散的现象不符，但当λ≤0.1时，λ大小对稀疏非负矩阵分解聚类的结果并无影响。
| λ | H稀疏度 |
| 0.001 | 0.5229 |
| 0.005 | 0.5242 |
| 0.01 | 0.5291 |
| 0.05 | 0.5338 |
| 0.1 | 0.5354 |
| 0.3 | 0.6608 |
| 0.5 | 0.6812 |
评估不同的波段数对SNMF-BS算法的影响，应用DB、KL和CH特征有效性的量度指标首先从波段聚类有效性角度对基于聚类波段选择进行评定。表 3反映了上海PHI数据波段聚类有效性，可见波段聚类为5组其聚类最有效。
| 波段聚类 | 11:{(2-14,48,51,71-76),(15-37),(38-47,49,50,63),(52-54),
(55-61),62,(64-70),(77,80,81-90),(78,79,91-100),(93,102,105, 108,111),(101-110)} | 7： (2-12,43-53,71-77),(13-42),54,(55-63),(64-70,111),(78-100),(101-110)} | 5： {(2-42),(43-54),(55-72),(73-100),(101-111)} | 3: {(2-32,101-111),(33-67),(68-100)} |
| DB | 2.4942 | 3.6564 | 0.8516 | 0.9528 |
| KL | 0.2466 | 0.2266 | 0.0636 | 0.2021 |
| CH | 21.4215 | 41.9393 | 295.5584 | 153.0772 |
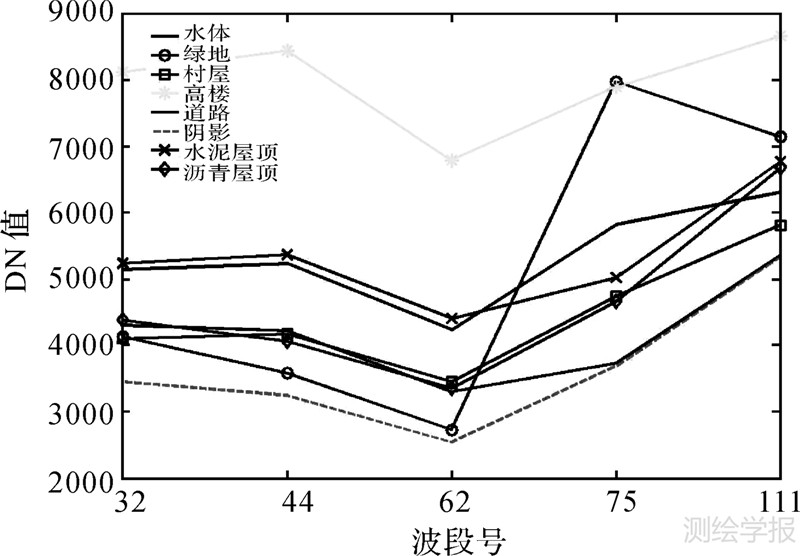
再对试验数据的波段选择结果从信息量、相关性和可分性3方面进行度量，得到表 4。通过表 3、表 4的分析可知上海PHI高光谱影像选择(32,44,62,75,111)5个波段能较好地对原始数据进行降维，其中选择第32波段(548.05nm)来反映水体在蓝绿波段的反射特性，第44波段(604.05nm)和红波段的第62波段(687.15nm)是植被的强吸收处，红波段的第62波段(687.15nm)和近红外波段的第75波段(749.00nm)能较好的区分建筑物屋顶(水泥混凝土材质和沥青瓦片材质)，第111波段(922.11nm)则能与红波段进行植被指数的运算。与之相对应的波段选择后的主要地物光谱信息如图 4所示，可见应用波段选择评价的波段优化选择在降维的同时能够最大限度地保留高光谱图像的光谱特征与其物理意义。
| 波段选择 | 信息量度量 | 相关性度量 | 可分性度量 |
| 33、43、54、59、62、67、73、77、79、108、110 | 1.1647 | 0.7024 | 0.4970 |
| 32、54、62、67、77、81、111 | 1.1368 | 0.6934 | 0.3905 |
| 32、44、62、75、111 | 1.1650 | 0.6886 | 0.5617 |
| 67、81、111 | 1.2052 | 0.8584 | 0.5539 |
|
| 图 4 波段选择后主要地物光谱值信息 Fig. 4 Subset bands Spectrum of different objects in PHI imagery |
为了评价SNMF-BS算法的可行性和实用性，选用基于波段排序的ID、MVPCA、和波段聚类的k-means、Sparse NMF(等价于k-means)与SNMF-BS对比分析。比较这几种算法的复杂度，发现基于乘法迭代规则的SNMF-BS算法复杂度与同为波段聚类的k-means算法和Sparse NMF的复杂度都为:O(NLKt)，MVPCA算法复杂度为:O(KL+N2)，ID算法复杂度最低O(L2N)具有相对较高的时间效率。其中，N为像素个数；L波段数目；K为聚类个数；t为迭代次数。为了进一步对比各个算法的计算复杂度，统计了各算法的运行时间。这些算法运行于配置为2.4GHz CPU和2.0GB内存的个人笔记本电脑上，表 5为不同算法对PHI-3影像波段选择的实际所用时间，可见SNMF-BS算法复杂度是一阶的，所耗时间与k-means算法相当，而较ID、MVPCA算法计算时间较长。
| s | ||||
| k | 5 | 10 | 15 | 20 |
| SNMF-BS | 16.4081 | 37.2543 | 44.1803 | 48.6347 |
| ID | 9.3981 | 20.4081 | 22.3924 | 25.3924 |
| MVPCA | 11.2668 | 21.2816 | 25.2876 | 28.2845 |
| k-means | 17.7786 | 35.8071 | 43.9202 | 46.7309 |
| Sparse NMF | 17.0974 | 36.9003 | 44.2014 | 47.0389 |
波段选择的目的是通过降维，提高分类的性能，因此选用SVM分类器进一步验证评价各种波段选择算法的性能及类别区分度。SVM分类器作为一种新颖的有效的统计分类方法，能够适用于高维特征、小样本与不确定性问题的研究，在高光谱遥感分类方面具有优越性。在试验中选择118训练样本和462个测试样本，如表 6所示。采用SVM分类器区分不同地物类别，并以分类精度为波段选择算法的衡量标准，对不同算法所选为3～30的波段数对分类正确率进行比较分析，见图 5。
| 类别 | 样本 | |
| 训练 | 测试 | |
| 水体 | 15 | 95 |
| 绿地 | 18 | 87 |
| 村屋 | 21 | 82 |
| 彩色沥青屋顶居民楼 | 14 | 36 |
| 水泥混凝土材质居民楼 | 7 | 21 |
| 高楼 | 10 | 45 |
| 道路 | 19 | 53 |
| 阴影 | 14 | 43 |
| 总计 | 118 | 462 |
|
| 图 5 SVM 的分类结果 Fig. 5 Classification results of SVM |
可见基于SNMF-BS算法和Sparse NMF算法进行分类的精度近似，高于其他波段选择算法。其他依次为k-means、MVPCA和ID。ID算法依据信息散度进行排序，其所选波段高度相关，造成分类精度较低。由此表明应用稀疏非负矩阵分解能实现高光谱影像的有效波段选取，且符合高光谱影像自身稀疏和非负的特性。从图中还能看出，对于SNMF-BS算法而言，5个波段的信息量最大，判别能力最强，取得了最好的分类正确率，且随着波段数的增加，所选出的波段之间的相关性开始增加，冗余波段(相关度高于一定阈值的波段)开始产生，冗余波段往往会干扰其他波段的判别能力，从而降低分类器的性能，减少分类正确率。对于该上海PHI数据，ID、MVPCA、k-means波段选择算法则在11～15个波段判别能力最强，取得了最好的分类正确率。
6 结 论非负矩阵分解可反映人类思维中“局部构成整体”的概念，这种稀疏认知机制可用于高光谱影像的稀疏表示。因此，本文提出SNMF-BS的高光谱影像波段选择。首先应用虚拟维数来确定波段选择数量，依据稀疏非负矩阵分解与概率潜语义分析聚类的等价性应用稀疏非负矩阵分解的系数矩阵对高光谱影像波段进行聚类，再从聚类中类别里选择信息量最大值的波段作为波段选择结果。由试验表明，这种基于无监督波段聚类的波段选择方法既可从聚类特征有效性角度来反映波段聚类的有效性，又可从信息量、相关性和可分性角度对选择后的波段子集进行分析，能最大限度地保留高光谱图像的光谱特征与其物理意义。进一步选用SVM分类器验证了SNMF-BS算法的实用性。
本文将高光谱影像三维立方体结构转变成二维结构，进行高光谱影像的二维非负矩阵分解。在今后的工作中，将尝试探索稀疏非负张量分解，由此可以避免高光谱数据从三维转变成二维的重塑空间结构步骤。
| [1] | EMMANUEL A C,LUIS O J R, MIGUEL V R. Unsupervised Feature Extraction and Band Subset Selection Techniques Based on Relative Entropy Criteria for Hyperspectral Data Analysis[C]// Proceedings of Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery. Orlando: SPIE, 2003: 462-473. |
| [2] | CHANG C I, DU Q, SUN T L, et al. A Joint Band Prioritization and Band-decorrelation Approach to Band Selection for Hyperspectral Image Classification [J]. IEEE Transaction on Geoscience and Remote Sensing, 1999,37(6): 2631-2641. |
| [3] | CHANG C I, WANG S. Constrained Band Selection for Hyperspectral Imagery [J]. IEEE Transaction on Geoscience and Remote Sensing, 2006, 44(6):1575-1585. |
| [4] | MOJARADI B, EMAMI H,VARSHOSAZ M, et al. A Novel Band Selection Method for Hyperspectral Data Analysis [C]//Proceedings of International Archives of Photogrammry, Remote Sensing and Spatial Information. Sciences, 2008:447-451. |
| [5] | MARTNEZ-US A, SOTOCA F, PLA J M, et al. Clustering Based Hyperspectral Band Selection Using Information Measures[J]. IEEE Transaction on Geoscience and Remote Sensing, 2007, 45(12):4158-4171. |
| [6] | QIAN Y, YAO F, JIA S. Band Selection for Hyperspectral Imagery Using Affinity Propagation [J].IET Computer Vison, 2009, 3(4):213-222. |
| [7] | SU Hongjun. Spectral-texture Feature Extraction and Multi-classifier Ensemble for Hyperspectral Imagery[D]. Nanjing: NanJing Normal University,2011:18-21.(苏红军. 高光谱影像光谱-纹理特征提取与多分类器集成技术研究[D]. 南京:南京师范大学,2011:18-21.) |
| [8] | THOMAS H. Probabilistic Latent Semantic Indexing[C]//Proceedings of the Twenty-second Annual International SIGIR Conference on Research and Development in Information Retrieval (SIGIR-99). New York:[s.n.],1999. |
| [9] | TAO Chao, TAN Yihua, PENG Bifa, et al. A Probabilistic Latent Semantic Analysis Based Classification for High Resolution Remotely Sensed Imagery [J]. Acta Geodaetica et Cartographica Sinica,2011,40(2):156-162.(陶超, 谭毅华, 彭碧发, 等.一种基于概率潜在语义模型的高分辨率遥感影像分类方法[J].测绘学报,2011,40(2):156-162.) |
| [10] | YI Wenbin, SHEN Li, QI Yinfeng, et al. The Hierarchical Clustering Analysis of Hyperspectral Image Based on Probabilistic Latent Semantic Analysis [J]. Spectroscopy and Spectral Analysis, 2011, 31(9): 2471-2475.(易文斌, 慎利, 齐银凤, 等.基于概率潜语义分析模型的高光谱影像层次聚类分析[J]. 光谱学与光谱分析,2011,31(9): 2471-2475.) |
| [11] | LEE D D, SEUNG H S. Learning the Parts of Objects by Non-negative Matrix Factorization [J].Nature,1999, 401:788-791. |
| [12] | KIM J, PARK H. Sparse Nonnegative Matrix Factorization for Clustering[R]. CSE Technical Report, Georgia: Georgia Institute of Technology, 2008. |
| [13] | LI J M, QIAN Y T. Clustering-based Hyperspectral Band Selection Using Sparse Nonnegative Matrix Factorization [J]. Journal of Zhejiang University-Science C, 2011, 12(7): 542-549. |
| [14] | DING C, TAO L, WEI P. On the Equivalence between Non-negative Matrix Factorization and Probabilistic Latent Semantic Indexing[J].Computational Statistics and Data Analysis,2008, 52(8):3913-3927. |
| [15] | HOYER P. Non-negative Sparse Coding[C]//Neural Networks for Signal Processing.[s.L.]:IEEE Workshop, 2002, 557-565. |
| [16] | SCHMIDT M N. Speech Separation Using Non-negative Features and Sparse Non-negative Matrix Factorization[EB/OL].[2011-08-07].http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1 .135 .9337. |
| [17] | BOUTSIDIS C, GALLOPOULOS E. SVD Based Initialization: A Head Start for Nonnegative Matrix Factorization [J]. Pattern Recognation,2008, 41: 1350-1362. |
| [18] | CHANG C I, DU Q. Estimation of Number of Spectrally Distinct Signal Sources in Hyperspectral Imagery [J]. IEEE Transaction on Geoscience and Remote Sensing, 2004,42(3):608-619. |
| [19] | LIU Y C,GAO X D,GUO H W,et al. Ensembling Clustering Validation Indices[J].Computer Engineering and Applications,2011,47(19):15-17,30.(刘燕驰,高学东,国宏伟,等.聚类有效性的组合评价方法[J]. 计算机工程与应用,2011,47(19):15-17,30.) |
| [20] | LI Xing,MAO Dingshan,ZHANG Lianpeng. Evaluation Method for Band Selection Algorithm of Hyperspectral Image[J].Geography and Geo-Information Science, 2006,22(6):34-37.(李行,毛定山,张连蓬.高光谱遥感影像波段选择算法评价方法研究[J]. 地理与地理信息科学,2006,22(6):34-37.) |
| [21] | HOYER P O. Non-negative Matrix Factorization with Sparseness Constraints[J]. The Journal of Machine Learning Research, 2004, 5(9): 1457-1469. |