2. 武汉大学 资源与环境科学学院,湖北 武汉 430079;
3. 上海市测绘院,上海 200063;
4. 国家基础地理信息中心,北京 100830
2.School of Resource and Environment Sciences,Wuhan University,Wuhan 430079,China;
3. Shanghai Surveying and Mapping Institute,Shanghai 200063,China;
4. National Geomatics Center of China,Beijing 100830,China
1 引 言
在传统制图学中,等高线综合是一项既需要严格遵照地图制图规范,又需要作业员具备丰富制图经验的再创造过程。
现有的等高线综合方法可以分为3大类:第1类是基于地貌结构线和等高线形状的直接成组综合;第2类是基于DEM离散点所携带的信息量,先对DEM进行综合,再回放其对应等高线的间接综合;第3类是基于分形学或小波理论的等高线综合,此外还有基于小波理论且顾及地形结构线的DEM多尺度综合法。第1类典型方法有文献[1]提出的等高线成组综合的必要性和基本条件;文献[2, 3, 4]提出的基于地貌结构线提取的等高线成组综合法;文献[5, 6]提出在等高线上顺序地每n个点保留1个点,设置最大距离阈值,根据偏角法寻找等高线上特征点并构造地貌特征线,同时联合运用Douglas-Peucker算法进行综合;文献[7]提出了在等高线图中提取排水系统、建立成组等高线弯曲和排水系统分支之间的联系,在对排水网络结构进行综合的基础上,成组删除等高线弯曲的综合方法。文献[8]提出基于B样条曲线蛇模型的等高线综合方法,其目的是避免等高线的相交和自相交。第2类等高线综合的典型方法有文献[9]提出的基于三维离散点信息量判别法的自动综合;文献[10]提出的利用空间平面夹角法、空间点到空间面的距离法,以及高程差法对TIN进行化简的方法;文献[11]提出的将Douglas-Peucker算法扩展到三维,并将其用在对散点DEM的综合上;第3类等高线综合的典型方法有文献[12]提出的基于Douglas-Peucker算法分维估值的单根等高线综合法;文献[13]提出的多进制小波及其在DEM数据有损压缩中的应用;文献[14]提出的基于小波理论的等高线多尺度表达;文献[15]提出的基于小波理论且顾及地形结构线的DEM多尺度综合法。其中第1类方法的特点是将所有等高线弯曲和地貌特征线建立联系,能保证成组综合后的等高线之间不会产生空间冲突,不会产生“有河没谷”的不合理现象,但是这些方法普遍比较复杂,综合速度较慢,且难以解决经综合后的水系与等高线套合的问题。第2类方法的特点是直接对地理信息而非地图信息进行综合,这样有利于多尺度数据景观模型的产生和利用;但是其中有的处理过程复杂且综合结果不稳定,往往与点子的处理顺序有关;有些是基于局部数据的处理,难以保留全局特征点,有“削高填低”的倾向,过多地损失了地理精度。上述的第3类方法中,基于分形理论和基于小波理论的算法针对的是单根等高线综合,尚缺乏与结构线的联系,对于需要在图形输出中出现原始数据里未被包含的新高程等高线(例如,原始等高距为20 m,目标数据等高距为50 m,凡高程为50 m单数倍的等高线,均不能通过化简原始等高线而获得)时,第1类与第3类方法尚无能为力。
本文要探讨等高线综合的根本意义,为了克服目前各种方法的缺点,尝试从另一种视角来看待等高线及其综合的实质,从而提出一种全局性的等高线的间接综合方法,即先将等高线看成是离散点集,在对离散点集全局性综合的基础上,再回放出等高线,并将其看做是等高线的综合结果。
2 等高线间接综合的理论依据 2.1 无格式DEM的概念数字高程模型(DEM)是通过有限的地形高程数据实现对地形曲面的数字化模拟[16]。根据DEM的发展,当前在地理信息和地图制图工程界里,DEM几乎已成为具有一定密度的规则格网式排列的高程集的代称。由于它使用方便、结构简单,记录紧凑,使它成为最普遍的存在形式。实际上,DEM格式并不局限于上述的那一种,比如下面列出的数据,尽管格式互不相同,但都符合DEM的定义:① 随机分布的三维离散点集(散点式DEM);② 等高线上的跟踪点系列(等高线DEM);③ 平行断面投影线上给定高程的点集(断面DEM);④ 规则格网(RSG)交点或中心点上的高程集(规则格网式DEM);⑤ 不规则三角网(TIN)顶点上的三维坐标集(TIN式DEM);⑥ 带有结构线与特征点的规则格网高程集(规则格网叠加特征点、特征线式的DEM)。
在以上各种格式的DEM中,①、②、③直接来自于测量;④、⑤为经后处理得到;⑥是直接测量结果与④的叠加。因此,不妨将DEM的格式由习惯性思维的一种扩大到多种,重要的是不同格式的DEM之间可以进行相互转换。凡是用于描述地表高程变化,而不考虑具体格式的点集,可以称之为无格式DEM。上述散点式DEM,就是无格式DEM。
2.2 等高线间接综合的基本思想由于地理信息科学、地图制图学等学科的发展,使得各种格式的DEM之间能以较高的效率和较小的信息量损失进行格式转换。因此,针对DEM的综合问题,可以将有格式DEM先“降格”成无格式DEM,即忽略其具体格式,只用其三维离散点这种无格式信息进行综合,即根据比例尺跨度所需要的信息量衰减比,适当删除描述地表的次要点,而保留其主要的地貌特征点,从而得到简化的三维点集地表描述模型。在此基础上,再恢复成所需格式。本文所谓的等高线间接综合思想,就是先将等高线DEM看做是无格式的散点,用下面要讲到的三维Douglas-Peucker算法进行综合,最后再将经综合的散点转化成所需格式(此处即指等高线),并把这样得到的等高线作为原始等高线的综合结果。
3 三维Douglas-Peucker的基本算法及其改进文献[17]提出用不断定义新基线、计算点线距以及将点线距的计算结果与预先设定的一个阈值进行比较,从而决定某曲线上的点是否应被删除的方法,来对一条原始曲线的形态细节进行化简。由于该算法能获得所有主要特征点,逼近精度高,算法本身也较简单,已成为地图制图和地理信息学中最常用的线划要素综合手段之一。
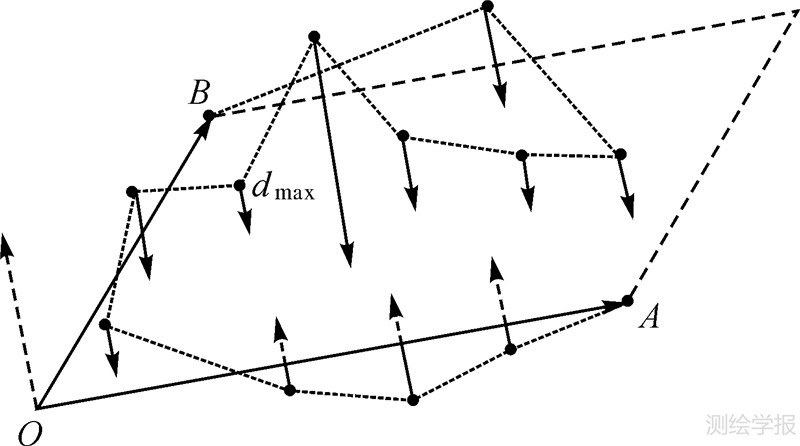
3.1 三维Douglas-Peucker算法简介文献[11]在此基础上,扩展性地提出了三维Douglas-Peucker算法[11],其本质就是不断定义新基面、计算地表点到基面的点面距以及将计算出的点面距与预先设定的一个阈值进行比较,从而决定地表上的这一点是否应被删除(见图 1),从而达到简化地表点的目的。
|
| 图 1 三维D-P算法中的首基面与点面距 Fig. 1 Initial base plane and point-plane distances of the 3D D-P algorithm |
在本文中,以后将“Douglas-Peucker算法”简称为“D-P算法”。
原点和首基面的确定:三维D-P算法首先在一群随机分布的三维离散点{Pi│i=0,1,…,n}中寻找出一个原点和第1个基面(首基面)。即当每个原始点都试做过原点O,且每次在剩余点集中选择两个点A和B,最终能获得最大矢量积OA×OB的绝对值时,点O、A、B就被确定。通过这3点的平面就是三维D-P算法的首基面(见图 1)。
将无序点集有序化:由于使用D-P算法针对的是有序点列,因此需要将看似无序的离散点进行排队。方法是:将点O作为P0,点A作为P1,B作为Pn存储到点列中。在原始点的剩余点集中,寻找并取出离开A点的三维距离最近的点作为P2插入点列,在剩余点集中,继续寻找并取出离P2点三维距离最近的点作为P3插入点列,直到取出最后一点作为Pn-1插在Pn之前即可。
点子的选取方式:点O、A、B被无条件优先选取。在排完序的点列中,分别计算点P2、P3、…、Pn-1到首基面的距离,如果所有的距离都小于预先设定的一个阈值,则这些点子全部被删除;否则取出具有最大点面距的点作为被选出的点Pi,这个点也被称为分裂点C。采用分而治之法,分别计算点P2、P3、…、Pi-1到基面OAC的距离,递归选取一个分裂点的原则如上所述,直至找不出新的分裂点;然后,分别计算Pi+1、Pi+2、…、Pn-1到基面OBC的距离,如上所述,递归选取出所有的分裂点后,三维D-P算法的整个综合过程便告结束。
3.2 算法特点图 2是3134个原始三维离散点以及将它们用本方法综合成1568个点和784个点后,用晕渲图表示的效果。

|
| 图 2 原始数据点及用3D D-P算法综合后的地貌表达效果 Fig. 2 Represented geomorphologic forms from source points and their generalized point-sets using 3D D-P algorithm |
从图 2可以看出:使用三维D-P算法综合离散点,无论是点子数减半还是再减半,主要地貌特征点总是会被优先保留,而被删除的点都是相对次要的点。根据这一特点,可以看出,此法可用于对随机分布的三维离散点的综合。
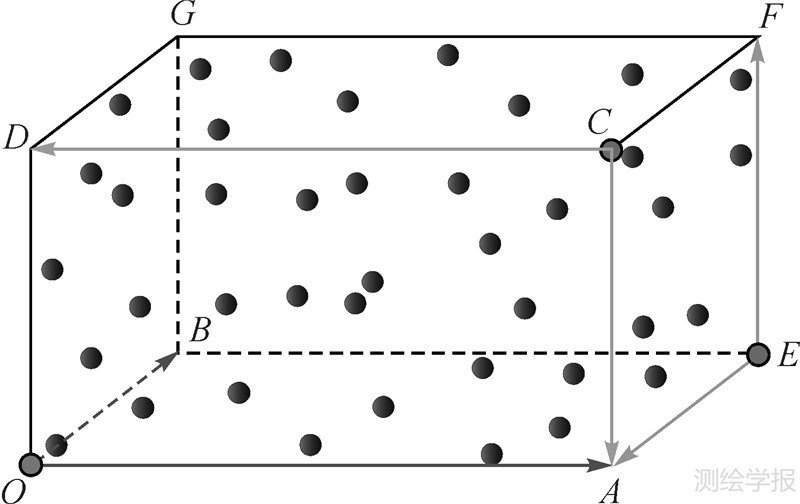
上述方法可以由计算机自动计算出确定首基面的3个点,但是效率却不能令人满意。其原因主要由于为确定首基面而寻找3个点的计算量相当可观,算法时间复杂度为O(n3)。当数据量较大时,时间、成本开销难以承受。因此,在实践中可以作出变通。图 3表示一个三维离散点集的最小外切长方体。可以人为地给出O、A、B点来确定一个首基面。O为该最小外切长方体OAEB-DCFG的一个角点,OA与OB为位于同一水平面上的该长方体上两根互相垂直的棱线。也就是说,原点O及两个形成最大矢量积绝对值的矢量终点A和B不必是原始点集的一部分,首基面人为地先确定为是经过O点的水平面。因为实际上地表点集的分布特点一般是水平方向上延展性很广,而在竖直方向上的起伏度相对很小,再加上点子的离散性,所以经这番变通后,与用本文已介绍的由计算机自动从原始点集中计算、选择出O、A、B,确定首基面后再用三维D-P算法进行离散点综合的结果往往大同小异,甚至可能完全相同。
3.3 特征点选取灵敏度不一致现象及处理虽然在综合过程中,基面会不断地变化,但基面总要通过原点O。换句话说,基面的选择受到一定的限制,再加上越是靠近原点的原始数据点因受到基面族的辐射效应影响,点面距就会越小,即越不易被这种方法选上。这种现象实质上就是特征点选取的灵敏度不均匀(虽然这种不均匀性不易被发现)。考虑到离散点集分布的随意性,对于长方体来说,可以进一步的变通:规定对原始点集用8个角点分别作为原点、经过每个原点可有3个长方体表面作为首基面。那么,共可有8×3=24个首基面与原点的组合来独立进行综合,将选出的24个点集进行“逻辑加”(即取其并集),作为选取的点集。它可被简称为“24合1”。从理论上讲,这种方法能克服对特征点选取灵敏度的不均匀现象,但是以如此增加算法复杂度作为代价却不值得。经理论推导与试验,只取3个正交的基面作为首基面,而对应的3个原点的选择原则是既不重复,也不与任何其他原点在同一棱线上。例如图 3中的第1个首基面是平面OAB,其中原点为O;第2个首基面是平面CDA,其中原点为C;第3个首基面是EFA,其中原点为E。这种方法简称为“3合1”。
|
| 图 3 用“3合1”的三维D-P算法综合离散点集前原点和首基面的确定方法 Fig. 3 Method for determination of origins and initial base-planes using “3 in 1” 3D D-P algorithm before generalizing a point-set |
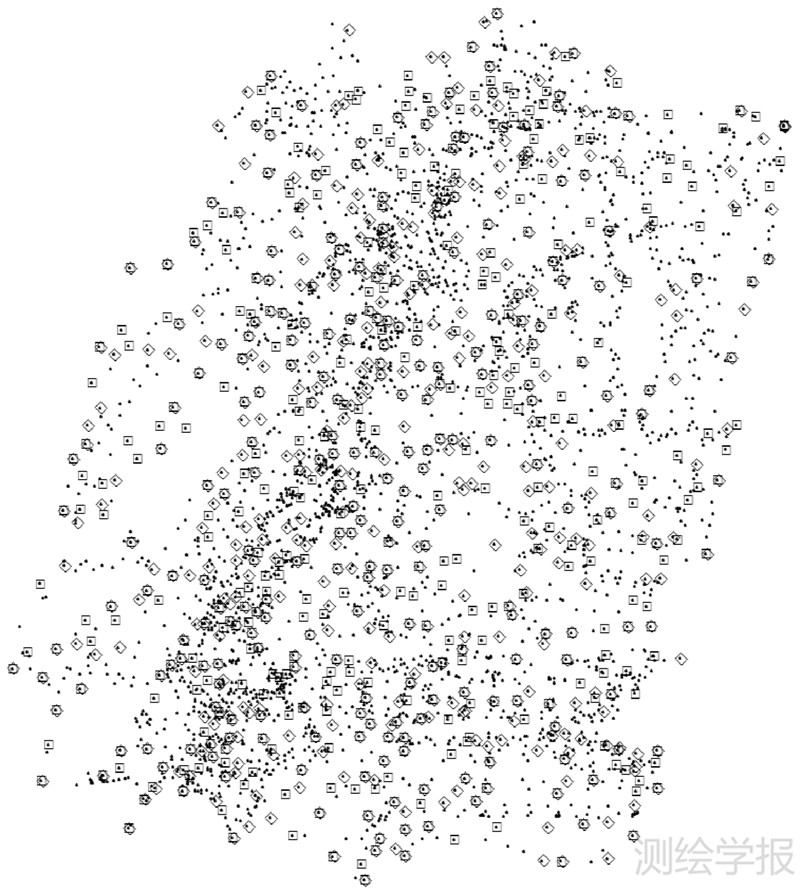
用“3合1”算法进行综合的实质就是先分别用上述3个原点及各自对应的3个不同首基面对同一套原始数据点进行3D D-P综合,得到3套综合后的点集,取这3个点集的并集,作为综合结果。显然,此法可以较彻底地避免对原始点集选点时灵敏度的不均匀现象。图 4表示用产生图 2(a)的那套原始散点进行两种3D D-P综合的结果。第1种为“一次性综合”法,即只用一个原点与一个首基面综合的3D D-P法,而第2种为“3合1”法。图中小黑点为3134个原始散点。正方形表示用“一次性综合”法选取的结果,菱形表示用“3合1”法综合的结果,而这两种方法都选出了525个点,其中有265个点是两种方法都一致选出的点。
|
| 图 4 用“一次性综合”与“3合1”法综合的结果与原始点的叠加比较 Fig. 4 The overlayed results between the original points and the selected points using the “one time” and “3 in 1” generalization methods respectively |
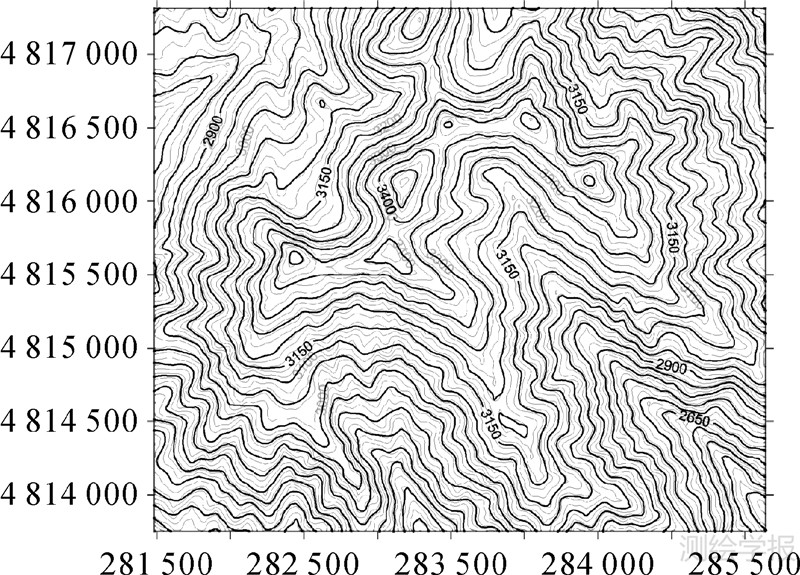
等高线间接综合后的初步结果:图 5是一幅综合前与用本文介绍的方法间接综合后的等高线叠置图。其中浅色等高线为1∶10万比例尺地形图的原始等高线,其等高距为20 m;黑色等高线是以1∶25万作为目标地形图比例尺的等高线综合结果,其等高距为50 m。同一制图区的图幅之所以在综合后几何尺寸未见缩小以及将两幅等高线图加以叠置,只是为了便于比较和分析。
|
| 图 5 用间接综合法综合前后的等高线叠置图 Fig. 5 Overlay of contours before and after generalization using the indirect method |
以此例为代表对综合结果的分析和讨论如下:
(1) 综合后等高线的精度能够得到保证,且当需要根据原始数据内插新等高线(例如图 5中高程为2650 m或3150 m这些50 m的单数倍等高线)时,该方法可以在不增加复杂度的情况下得到。
(2) 一般情况,相邻等高线之间的拓扑关系及协调套合关系能良好保留,且即使在没有刻意寻找地貌结构线的情况下,综合后的等高线也能自然保留主要结构线,而弱化甚至消除次要结构线。
(3) 同名等高线在综合后无论对于正向还是负向地貌,都有减小波动起伏的效果,但形态自然,由于曲率绝对值变小,加上等高距变大,故即使按比例缩小后,在地图印刷或地图阅读中,等高线均不会产生拥挤、模糊、难以辨认的情况。
(4) 至于综合后的等高线,其综合程度能否满足1∶25万地形图等高线表达的要求,一时难以判定。严格地说,这个问题在常规手工制图综合中也没有很好解决。如何自动掌控地图制图综合的程度问题,除了本文第5节的初步设想外,准备另文从信息量的应有衰减比着手,详加探讨。
(5)用该方法间接综合等高线得到的结果,与目前常规手工制图综合规范所要求的结果之间还存在一定差异。其主要表现在,目前等高线制图综合规定,对于以正向地貌为主的地域原始等高线,当谷间距小于一个阈值时,就要成组拉直相邻的、较次要的谷底等高线弯曲,这相当于总是填平次要沟谷,夸大了正向地貌;而用本法综合得到的等高线,随着比例尺的逐渐缩小,总是逐渐抑制原始等高线的起伏和振荡幅度,即对于正向或负向地貌都有“削减”的效果(见图 5)。笔者认为,前者对地貌的“塑形”效果较为明显,简化了地貌形态,令地图读者印象深刻,但当比例尺连续变小时,所得到的综合结果之间会有跳跃,且由于一味夸大正向地貌部分,地貌的实际变形较大;后者更符合读者视点在逐渐远离研究区过程中(相当于制图比例尺渐渐缩小),地图读者对地貌起伏幅度(无论是沟谷还是山脊)连续变小的感受,且由于对正、负向地貌等高线的弯曲都有抑制,故地貌表达的总偏差较小。而这两种等高线的表达方法,都能使得比例尺缩小后,等高线的形态满足清晰可辨的要求。
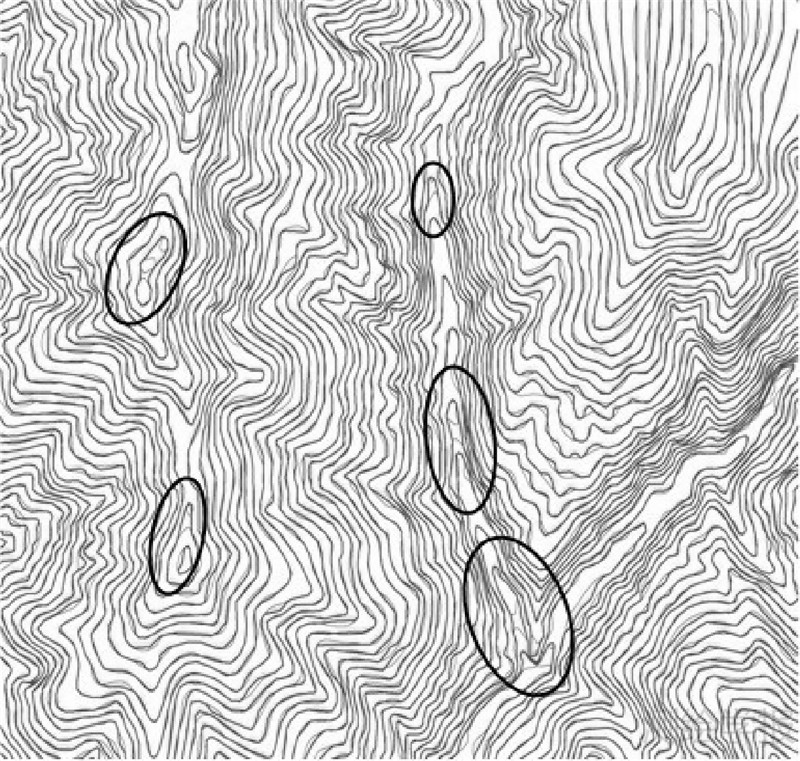
4.2 等高线拓扑关系的偶然变化分析当用3D D-P算法综合好离散点集,并据此回放出等高线时,有时等高线的拓扑结构与原图相比会出现一些变化。为了详细比较起见,图 6为综合后等高线几何尺寸及等高距暂不变,且将原图等高线(深色)与综合后等高线(浅色)叠置显示。其中被椭圆标注的谷地或山包等高线,由原来一根等高线变为2根、甚至3根同名等高线。
|
| 图 6 综合后等高线的局部拓扑结构的偶然变化 Fig. 6 Occasional change of local topological structure for contour lines after generalization |
究其原因,虽然各种格式的DEM之间理论上可以进行转换,只要方法得当,转换效率可以较高,但不能保证信息在转换中一点不受损失。例如从离散点集转换成等高线,显然属于那种信息载体从小到大的转换(等高线可看做具有无穷多离散点的有序集合)。这样,若不给出足够的转换控制条件,有可能出现拓扑结构变化。
可以模仿人工综合等高线时先在大脑中产生隐性地貌结构线,并在等高线综合时,使新等高线不破坏作业员大脑中的隐性结构线为原则。可在综合前,逐根利用原始等高线,从曲率绝对值最大点出发,连续构建平三角形链,计算且连接出其主要三维中位线而得到近似地貌结构线[18]。在综合好等高线上的离散点,开始回放等高线前,才将用以上方法找到的主要地貌结构线,作为生成等高线时的控制条件,从而克服等高线拓扑结构的变化(见图 7(a)、图 7(b),为便于比较,这两幅图的尺寸及等高距暂时相同)。

|
| 图 7 借助主要地貌结构线回放的综合前后等高线对比 Fig. 7 The comparison of source contour lines and generalized result contours with the help of major geomorphologic structure lines |
在此例中,原始等高线的点数是8882,结果等高线是利用887个3D D-P选取点,并在主要地貌结构线参与下回放出来。
5 结 论通过用3D D-P算法对等高线进行间接综合的试验和改进,可以得出以下结论:
(1) 基于三维D-P算法的等高线间接综合,在等高线的综合精度、等高线之间的套合协调性、等高线拓扑结构和地貌主要特征的保留、综合后等高线的图面清晰度等方面,都能符合制图综合的要求。
(2) 用本文方法间接综合等高线,对等高线数据要求不高。例如遇到原始等高线由于局部陡峭地区过于拥挤而只绘出了计曲线,或用陡崖符号代替局部等高线,其原始数据均能被正常使用;若原始数据除等高线外,还能提供其他信息,如碎部点、特征点、地貌结构线或者对应的RSG等,也能作为输入数据参与计算。
(3) 同时,用本文方法综合等高线对输出数据的要求也容易满足,例如,可以要求输出小于原始数据比例尺的任意比例尺的等高线、也可以要求输出原始数据里没有包含的其他高程的等高线。
(4) 目前用本文方法的综合结果与常规手工法综合的结果大同小异。但由于其自动化程度有所提高,可大幅提高制图综合的经济性以及综合数据的现势性。
面向制图实际生产要求,以下问题必须很好地得到解决,才能使本文方法真正用于实践:① 海量数据的加速综合;② 综合程度自动控制的手段;③ 地貌与水系综合结果之间的协调套合[19 ,20]。
| [1] | HENTSCHEL W. Zur Automatischen Hhenlinien-Generalisierung in Topographischen Karten[D]. Hannover:Diss. University, 1979. |
| [2] | WU Hehai. Prinzip und Methode der Automatischen Generalisierung der Reliefformen [J]. Nachrichten aus dem Karten und Vermessungwesen, 1982, 85:163-174. |
| [3] | WU Hehai. On Automated Generalization of Relief Forms [J]. Journal of the Wuhan Technical University of Surveying and Mapping, 1995, 20 (sup):1-6. (毋河海. 地貌形态自动综合问题 [J]. 武汉测绘科技大学学报, 1995, 20(增刊):1-6. ) |
| [4] | FEI Lifan. Experiments of Group Generalization of Contour Lines for Topographic Maps [J]. Journal of the Wuhan Technical University of Surveying and Mapping, 1993, 18 (sup):6-22 . (费立凡. 地形图等高线成组综合的试验[J]. 武汉测绘科技大学学报, 1993, 18 (增刊):6-22.) |
| [5] | GKGZ T,MEHMET S. A New Approach for the Simplification of Contours [J]. Cartographica, 2004, 39(4):37-44. |
| [6] | GKGZ T. Generalization of Contours Using Deviation Angles and Error Bands [J]. Cartographic Journal, 2005, 42(2):145-156. |
| [7] | AI Tinghua. The Drainage Network Extraction from Contour Lines for Contour Line Generalization [J]. ISPRS Journal of Photogrammetry & Remote Sensing, 200, 62(2):93-103. |
| [8] | GUILBERT E, SAUX E. Cartographic Generalisation of Lines Based on a B-spline Snake Model [J]. International Journal of Geographical Information Science, 2008, 22(8):847-870. |
| [9] | WEBER W. Automationsgestützte Generalisierung. Nachrichten aus dem Karten- und Vermessungswesen [J]. Frankfurt am Main, 1982, 88 (1):77-109. |
| [10] | CAI Xianhua, ZHENG Tiandong. A Study of DEM Data Compression and Its Algorithm [J]. Bulletin of Surveying and Mapping, 2003(12):16-18. (蔡先华, 郑天栋. 数字高程模型数据压缩及算法研究 [J]. 测绘通报, 2003(12):16-18. ) |
| [11] | FEI Lifan, HE Jin, MA Chenyan, et al. Three Dimensional Douglas-Peucker Algorithm and the Study of Its Application to Automated Generalization of DEM [J]. Acta Geodaetica et Cartographica Sinica, 2006, 35 (3):278-284. (费立凡, 何津, 马晨燕, 等. 三维Douglas-Peucker算法及其在DEM 自动综合中的应用研究 [J]. 测绘学报, 2006, 35(3): 278-284. ) |
| [12] | WANG Qiao, WU Hehai. Fractal Description and Automatic Generalization of Map Information [M]. Wuhan: Press of Wuhan Technical University of Surveying and Mapping, 1998:162-168 (王桥,毋河海. 地图信息的分形描述与自动综合研究 [M]. 武汉:武汉测绘科技大学出版社, 1998:162-168.) |
| [13] | WAN Gang, ZHU Changqing. Application of Multi-band Wavelet on Simplifying DEM with Loss of Feature Information[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 36-40. (万刚, 朱长青. 多进制小波及其在DEM数据有损压缩中的应用[J]. 测绘学报, 1999, 28(1): 36-40.) |
| [14] | WU Fan, ZHU Guorui. Multi-scale Representation and Automatic Generalization of Relief Based on Wavelet Analysis [J]. Geomatics and Information Science of Wuhan University, 2001, 26 (2):170-176. (吴凡, 祝国瑞. 基于小波分析的多比例尺地形表达及自动综合[J]. 武汉大学学报:信息科学版, 2001, 26 (2):170-176.) |
| [15] | YANG Zuqiao, GUO Qingsheng, NIU Jiping, et al. A Study of Multi-scale DEM Representation and Topographic Feature Line Extraction [J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2):134-137. (杨族桥, 郭庆胜, 牛冀平, 等. DEM 多尺度表达与地形结构线提取研究[J]. 测绘学报, 2005, 34 (2):134-137. ) |
| [16] | TANG Guoan, LIU Xuejun,LV Guonian. Principle and Method of Digital Elevation Model and Geo-science Analysis[M]. Beijing:Science Press, 2005. (汤国安,刘学军,闾国年.数字高程模型及地学分析的原理与方法 [M].北京:科学出版社,2005.) |
| [17] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature [J]. The Canadian Cartographer, 1973, 10(2):112-122. |
| [18] | WU Fan, SU Weimin, YANG Yingwei, et al. Extracting Terrain Features from Contour Maps Based on United Delaunay Triangulation Model [J]. Journal of China University of Mining & Technology, 2007, 36(2):172-176. (吴凡,粟卫民,杨英伟,等. 基于联合Delaunay三角网的等高线地形特征提取研究 [J]. 中国矿业大学学报, 2007, 36(2):172-176.) |
| [19] | WANG Donghua, LI Li. Tests of Contour Interpolation Using DEM Data and Their Fitting with River System [J]. Science of Surveying and Mapping, 1988 (4):14-19. (王东华, 李莉. 利用DEM数据内插等高线与水系套合试验 [J]. 测绘科技动态, 1988 (4):14-19.) |
| [20] | CHEN Jun, LIU Wanzeng, LI Zhilin, et al. The Calculation Method of Refined Topological Relationships between Line Objects [J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3):255-260. (陈军,刘万增,李志林,等. 线目标间拓扑关系的细化计算方法 [J]. 测绘学报, 2006, 35(3):255-260.) |


